灵敏度分析在数控机床精度优化中的应用研究现状*

项四通，吴铖洋

（宁波大学，宁波 315211）

数控机床能加工各种复杂工件，生产效率高、灵活性好且装夹时间短，对提升我国制造业水平具有举足轻重的作用。由于机床制造与安装过程中存在偏差，导致一定程度的几何误差。后者直接映射到工件尺寸上，影响加工精度，因而需要对其进行补偿。但是，由于几何误差较多，逐项测量并补偿全部几何误差工作量较大，因而需要辨识出关键几何误差，从而提高补偿效率。

灵敏度分析是一种研究物理系统的输出对系统输入参数变化敏感程度的方法，能有效识别对系统输出变化最敏感的参数。近年来，灵敏度分析逐渐成为机床精度优化领域的研究热点。本研究综述了灵敏度分析在数控机床精度优化中的应用研究现状，并进一步总结现存研究难点，展望其发展趋势。

灵敏度分析方法

数学模型是工程决策中的重要工具。随着日益增强的计算能力和日益丰富的可用数据，模型日趋复杂，其输入参数亦随之增多，必须理解这些输入参数的不确定性对模型输出结果的影响。

灵敏度分析是用于研究模型不确定性的一种重要工具，可定义为“模型输出的不确定性如何分配到模型不同输入来源的研究”[1]。如图1所示，它与“不确定性分析”密切相关，但有所不同。不确定性分析侧重于外部因素干扰导致模型输入参数改变时，分析模型输出的不确定性。而灵敏度分析侧重于模型输出产生不确定性变化时，分析由不同输入参数变化导致的影响程度。

图1 灵敏度分析与不确定性分析Fig.1 Sensitivity analysis and uncertainty analysis

根据输入参数是否同时变化，可将灵敏度分析分为局部灵敏度分析和全局灵敏度分析[2]。局部灵敏度分析仅检验单个参数的变化对输出结果的影响程度，其他参数只取中心值；全局灵敏度分析检验多个参数同时变化及参数之间的相互作用对输出结果的影响，其结果受多个输入参数影响。

1 局部灵敏度分析

局部灵敏度分析亦称“一次变化法”[3]，仅检验一个参数，其他参数取中心值，评价输出结果在该参数变化时的变化量。主要有两种方法： （1）因子变化法，如将输入参数增加或减少10%； （2）偏微分法，即模型输出对输入变量求偏微分，如式（1）所示。

式中，Si为第i个输入参数的灵敏度，xi为输入参数，f（x）为模型输出。

在机床精度优化方面，偏微分法是最常用的局部灵敏度分析方法，通过机床空间误差模型对某个几何误差求偏微分来估算该几何误差的灵敏度大小[4]。该方法机理简单，可操作性强，但存在以下缺点：（1）一次仅分析一项误差，计算效率较低； （2）仅考虑单项几何误差的变化，将其他几何误差视为固定值，忽略了实际几何误差随运动位置而变化，以及几何误差间的耦合作用，影响了分析结果； （3）求偏微分仅得到解析关系，忽略了误差本身数值大小。

2 全局灵敏度分析

全局灵敏度分析方法分为定性分析与定量分析[5]。前者亦称“因子筛选灵敏度分析”，仅定性分析输入参数的不确定性对输出结果的影响程度大小，以较小计算量获取各输入参数灵敏度大小的排序。后者定量给出各参数的不确定性对输出结果不确定性的贡献度，其计算量较大，但准确性较高。

2.1 定性全局

傅里叶幅度灵敏度检验法[6]（Fourier amplitude sensitivity test，FAST）适用于非线性、非单调性模型的灵敏度分析，通过引入一个独立参数，将多维参数空间内的积分转化为一维参数的积分。首先对各参数给出一个整数频率，将模型转换为该参数的周期函数，然后根据傅里叶变换分析输出结果，获取各频率对应的傅里叶幅度值。

标准化回归系数法[7]（Standardized regression coefficients，SRCs），也称“多元回归法”，基于拉丁超几何体取样，将每个参数的概率分布函数的纵轴（0～1）分成几个等间隔区间，每个区间分别对应横轴参数的一个等概率区间。若一个模型有n个参数，每个参数的概率分布分为m个区间，则有n×m个组合。矩阵的每一行作为各参数的输入值，获取模拟结果。最终，各参数的灵敏度大小可用模拟结果与各输入参数的多元线性回归系数或偏相关系数表示。

Morris法[8]能够对参数的灵敏度排序及参数间相互作用进行全局分析，其优势是计算量较小。该方法具有随机性，一次采样易产生误差，因此可进行多次重复，取平均值反映输入参数的灵敏度。其标准差可用于反映参数间相互作用，标准差的大小可反映相互作用强弱。该方法可简单准确地确定各参数灵敏度大小，可用于排除灵敏度较小的参数，再对其余参数进行定量全局灵敏度分析。

2.2 定量全局

定量全局灵敏度分析可定量确定各参数对于输出结果不确定性的贡献度，主要有Sobol法和傅里叶幅度灵敏度检验扩展法（Extended Fourier amplitude sensitivity test，EFAST）。上述两种方法均基于方差原理，认为方差可完全反映输出结果的不确定性；不仅计算参数对输出结果的单独影响，还考虑参数间的相互作用。

Sobol法[9]的基本原理为方差分解，首先将系统模型分解为单个参数及多个参数相互组合的函数，然后求出每个参数对应的灵敏度系数。该方法将模型视为黑箱，运用“蒙特卡罗”求积分法求出总方差及偏方差，获取一阶灵敏度系数和总灵敏度系数[10]。

傅里叶幅度灵敏度检验扩展法[11]结合Sobol法与FAST法的优点，由傅里叶变换获取傅里叶级数频谱，分别计算由每个参数及参数的相互作用所引起输出结果的方差。EFAST的优点在于精度相仿的前提下，计算量远小于Sobol法。Sobol法需通过两次取样得到某参数的一次灵敏度和总灵敏度，而EFAST仅需一次取样即可获得某参数的一次灵敏度和总灵敏度。

表1总结了上述方法的优缺点[12]。目前，Sobol法和EFAST法是较为准确、应用较为广泛的两种灵敏度分析方法。

表1 灵敏度分析方法对比Table 1 Comparison of sensitivity analysis methods

近年来，灵敏度分析逐渐成为机床关键误差辨识领域的研究热点，常应用于机床精度设计与工件加工精度分析。目前，灵敏度分析以面向机床精度设计居多，面向工件加工精度较少。

在机床精度设计方面的应用

精度设计是提高数控机床运动精度的重要方法，误差灵敏度分析则是机床精度设计的重要理论依据。首先，根据各误差对机床空间精度的影响程度确定误差灵敏度系数。然后，根据误差灵敏度系数，在机床工作空间内搜寻关键结构或关键误差。最终，在机床设计阶段对关键结构或误差进行针对性控制，通过公差设计，提升关键零部件的制造精度，从而提高机床运动精度。

在机床精度设计应用方面，灵敏度分析常用于公差设计、关键结构与关键误差辨识两个方面。前者对应机床设计阶段，通过“误差防止”提高机床精度；后者对应机床加工阶段，通过“误差补偿”提高机床精度。

1 机床公差设计

在机床结构设计与装配阶段，公差设计不仅影响机床运动精度，同时决定了装配成本。目前机床装配工艺大多依赖于设计人员经验，缺乏量化的装配测量工艺研究，导致装配过程效率较低。郭俊康等[13]根据灵敏度分析提出了基于误差状态最优估计的精密机床装配工艺决策方法，根据加工件的精度要求进行机床运动轴公差设计。宋轶民等[14]将影响末端姿态精度的几何误差分离为可补偿误差与不可补偿误差两类，对于不可补偿误差，以灵敏度分析确定公差分配权重；将不可补偿误差的公差值放松至最大可行区间，借助遗传算法实现了精度设计。

目前，公差设计逐渐转向公差优化设计，即在达到运动精度要求的前提下，尽可能降低成本。通过灵敏度分析，可获得公差对机床运动精度的贡献度，为改进公差设计结果提供依据。公差设计的具体方法为：将运动轴几何误差的公差带作为自变量，将机床运动精度作为因变量，利用蒙特卡洛方法和数据回归等方法，找到两者间的映射关系；在此关系基础上，根据实际检验要求，设计各运动轴几何误差的公差带。

公差优化设计的关键为建立目标优化函数，并求解各项几何误差的最优公差带。常见的目标优化函数如式（2）所示，并采用遗传算法求解此优化问题，最终得到在最低成本下的误差公差带。

式中，Ci为成本函数，表示第i项几何误差ei的公差带Vi决定的成本，Ex，Ey，Ez分别表示由各几何误差引起的X、Y、Z方向的空间误差。

刘奕颖等[15]采用正交试验得到精度要求与机床几何误差公差带之间的对应关系，基于多元线性方法进行灵敏度分析。采用自适应遗传算法针对精密坐标镗床的29项几何误差进行公差带设计与分配，在保证工件加工精度达到要求且成本最低的前提下，放宽了机床装配精度要求。

Wu等[16]基于正交试验溯源了三轴数控机床中的13项关键几何误差，并通过求解优化目标函数，给出了IT2～IT10不同公差等级下各关键误差的公差带。该方法在成本函数中同时考虑了夹具成本、制造成本与失效成本。Cai等[17]在目标函数中同时考虑失效概率、制造成本与预期质量损失，且在约束条件中增加了平均失效概率与最大失效概率，如式（3）所示。

式中，C表示总成本；Cfix表示夹具成本；Ci/σi表示第i项几何误差公差带决定的制造成本；Cfs表示失效成本；Pfs表示失效概率。

Cheng等[18]基于Sobol法计算出数控机床几何误差的一阶灵敏度与全局灵敏度，并将灵敏度分析结果集成于成本函数中，从而进行公差优化设计，如式（4）所示。

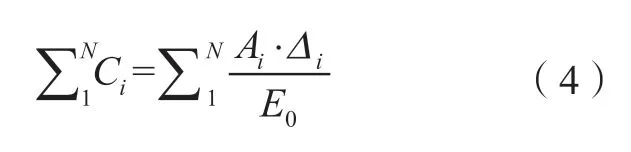
式中，N表示几何误差数量；Ci表示对于误差i的成本函数；Ai表示误差i的灵敏度；Δi为误差i的公差带；E0为误差初始值。

此外，Tian等[19]针对1台四轴数控机床，将机床的几何误差分为可补偿与不可补偿两类。可补偿误差可通过补偿实现精度提升，只有不可补偿误差需进行公差设计。Ni等[20]针对并联主轴，分析了影响主轴精度的运动副，也将误差分为可补偿与不可补偿两类，并对不可补偿误差进行灵敏度分析与成本目标函数优化，并求解出最优公差带。Zhong等[21]通过偏微分法计算装配误差对机床运动精度的灵敏度，判断出最关键的装配误差，并通过调整对应导轨安装松紧程度提高机床的运动精度。

2 机床关键结构与关键误差辨识

数控机床几何误差较多，逐项测量并补偿全部几何误差的工作量较大，影响补偿效率。因此，在机床误差补偿阶段，通过灵敏度分析判别出影响机床运动精度的关键结构或关键几何误差，仅对关键结构或关键误差进行补偿，从而提高补偿效率。

关键结构与关键误差的具体辨识步骤如下：（1）利用齐次坐标变换和多体系统理论建立数控机床的空间误差模型；（2）通过灵敏度分析确定各几何误差对机床精度的影响程度，确定关键结构或关键几何误差；（3）重点设计关键机床结构，通过逆运动学补偿关键误差。

在机床关键结构辨识方面，李天箭等[22]通过求解机床大件结构和整机的固有频率对于刚度、质量的灵敏度，确定结构薄弱环节，明确动力学优化方向；采用模态预测和灵敏度分析计算出合理的质量与刚度，提升机床的大件结构及整机的动态性能。最终，通过上述优化设计，将动态特性薄弱环节即主轴箱的占动特性提升50%以上，将整机固有频率提升11.9%。Fu等[23]提出了数控机床几何误差贡献度建模和灵敏度评估方法，根据机床空间误差模型及几何误差的微分变化，分析各几何误差的贡献度，从而建立各轴的误差灵敏度矩阵，最终以误差贡献度和误差灵敏度系数评估机床的关键轴，为机床设计与制造提供有效指导。Cheng等[24]采用Morris法进行灵敏度分析，判断出Y轴导轨精度为影响机床空间精度的主要因素，更换导轨后的机床Y向运动精度提高20%，验证了灵敏度分析在关键误差补偿方面的可行性。

在机床关键误差辨识方面，杨赟等[4]以30台立式加工中心的误差平均值为先验数据，基于偏微分方法进行灵敏度分析，求解了一类结构立式加工中心的关键几何误差，有助于批量提高机床精度与补偿效率。Chen等[25]利用均匀采样方法将机床工作空间离散为若干点，并提出Spearman等级相关方法分析单项误差与整个采样工作空间姿态误差之间的关系，最终辨识出四轴机床的10项关键误差，通过对测试路径的偏差进行补偿，将精度提高86.5%。Guo等[26]基于EFAST，辨识出五轴机床的13项关键几何误差，建立了多目标质量损失和精度鲁棒性权衡函数，利用遗传算法求解得到误差值的最佳补偿量，补偿后运动轨迹精度提高73.7%。该方法充分考虑了机床工作空间中几何误差的概率分布，克服了特定位置分析的缺陷。Liu等[27]基于Sobol法对双主轴对称超精密滚筒车床的几何误差进行全行程灵敏度分析，并以平均灵敏度系数评价各几何误差对全行程加工精度的总体影响。灵敏度分析结果表明，由于误差累积效应，当任意平动轴的移动距离增大时，该轴产生的敏感误差对加工精度的影响随之增大。余文利等[28]采用EFAST分析和量化几何误差灵敏度，识别出三轴数控机床的10项强耦合的关键几何误差，并利用方差与灵敏度系数之间的定量关系来补偿机床几何误差的随机特性。郭世杰等[29]采用拉丁超立方抽样方法对三轴数控机床整个工作空间抽样，确定各误差元素引起的空间几何误差，并通过相关性分析辨识出关键几何误差，有效避免了单因素分析的缺陷，补偿后运动轨迹的垂直度和圆度均提高70%以上。

此外，灵敏度分析在机床精度保持性研究方面亦有应用。王永青等[30]采用Sobol法，确定了各几何误差时变状态对机床空间位置精度保持性的影响，并以某三轴立式加工中心的9项关键精度指标进行了为期400 d的跟踪检测，分析出机床空间精度保持性随时间的变化规律，完成误差灵敏度定量评估。Niu等[31]为评估机床在长工作时间下的精度保持性，提出了一种基于误差非线性相关的加工精度可靠性分析方法，利用多体建模技术确定了加工精度与误差间的非线性关系，通过引入并计算偏相关系数，分析了误差相互作用对加工精度可靠性的影响。

在工件加工精度方面的优化应用

由于实际加工中刀具路径不同，工件受几何误差的影响不同，导致影响工件加工精度的关键几何误差不同于影响机床整机精度的误差。由于工件的加工精度是评价机床精度的最终标准，在保证机床自身精度的基础上，需要针对不同工件辨识关键几何误差。

面向工件加工精度的关键几何误差辨识中，考虑工件形状至关重要。以五轴加工为例，工件结构通常较为复杂，包含各类平面特征（如孔、槽、斜面等）与各式曲面区域（如凹面、凸面、鞍面等）。上述结构的切削路径各不相同，不同切削路径映射对应的几何误差，因而每个特征与区域的加工精度受几何误差的影响程度有所不同。如图2（a）所示，典型曲面可按形状指数S在[-1, 1]之间变化，分为凹面、凸面与鞍面共10种曲面类型[32]，在加工时受机床几何误差的影响程度不同。如图2（b）所示，具有相同形状指数S的曲面，若弯曲指数C不同，它们所对应的几何误差亦不同。

图2 不同形状指数与弯曲指数下的曲面Fig.2 Curved surface under different shape indices and deformation indices

传统的灵敏度分析方法通常采用整个加工区域的灵敏度分析，然而由于几何误差在工件不同区域对其形状误差的影响不同，可能影响灵敏度分析结果，从而降低补偿精度。因此，Fan等[33]根据S件开闭角和扭曲角将工件分为5个区域，提出一种定量间隔灵敏度分析方法，并辨识出各区域的关键几何误差，最终通过仿真和试验证明了该方法的可行性和有效性。

Tao等[34]利用随机森林对任意曲面的几何误差进行排序分析，首先将工件表面沿刀具轨迹离散，建立包含21项几何误差、工件形状误差和尺寸误差的误差数据集；然后通过对误差数据集应用随机森林，将关键几何误差的识别问题转化为特征选择问题，最终通过数值仿真分析了各几何误差对4种典型曲面尺寸精度的影响程度，识别出关键几何误差，并加工正弦网格曲面进行试验验证。Li 等[35]通过灵敏度分析阐明了刀具轨迹误差与进给轴误差运动的关系，以五轴联动加工过程中的自由曲线轨迹为基础，建立了各刀具中心点的曲面坐标系，定义了刀具轨迹及其误差。然后，定义了一个新的灵敏度系数来研究轨迹误差与误差运动之间的关系。最终进行圆锥台和S件加工试验，该灵敏度分析方法可判别轨迹对误差运动是否敏感。

在复杂机械零件的加工精度优化方面，学者们也开展了研究工作。Chen[36]、唐宇航[37]等面向S件，建立直纹面模型与加工误差映射关系，基于灵敏度分析分别在车铣复合中心和五轴龙门机床上辨识出关键几何误差，最终提高加工精度。付国强等[38]建立了五轴机床运动轴几何误差贡献值模型并基于灵敏度分析确定了几何误差影响机床精度的关键运动轴，最终以复杂鼠标曲面为例，提高了工件的五轴加工精度。面向齿轮的加工精度补偿中，Xia等[39-40]考虑齿轮磨削工艺的材料去除机理，建立了几何误差与齿面位姿误差之间的映射模型，直接揭示了几何误差与齿面误差的映射规律；在此基础上基于全局灵敏度分析确定了影响齿廓和螺旋偏差的关键几何误差，简化了误差补偿表达式并提高了齿轮加工精度；最终将该轮廓误差降低了43.27%。面向光学自由曲面的加工精度补偿中，Yao等[41]首先建立了考虑几何误差的超精密金刚石车削中心的运动学误差模型；然后通过对误差分量的灵敏度分析，得出影响加工精度的关键误差，最终提出了一种减小或消除相应机械系统定位误差的对准方法，从而提高被加工曲面的成形精度。Liu等[42]也面向超精密金刚石车削中心，将机床误差分为5类，并基于灵敏度分析判定了平面与球面的关键误差，提高了最终的加工精度。

机床精度优化应用中的现存问题与后续研究方向

本研究对近5年灵敏度分析在数控机床精度优化中的最新应用研究进行了系统综述，着眼于更高精度的数控加工精度。当前的灵敏度分析方法仍存在许多问题与不足，需要从以下5个方面进行深入研究。

1 机床误差关系复杂导致关键误差辨识困难

学者们采用各种灵敏度分析方法对机床进行关键误差辨识，但由于机床误差关系复杂，导致关键误差辨识困难。具体表现为： （1）机床结构种类繁多，且不同机床结构下的关键误差不同； （2）待加工的工件形状各异，不同形状的工件所对应关键误差不同； （3）机床几何误差与位置有关，因而工件在机床不同加工区域下的关键误差不同； （4）机床几何误差间存在复杂的耦合关系，直接影响关键误差的辨识结果。因此，复杂曲面工件分区域下的关键误差辨识、典型曲面工件在常见机床结构下的关键误差库建立、几何误差间耦合关系等问题值得未来深入研究。

此外，机床几何误差可分为平动误差和角度误差两类，平动误差的单位是μm，角度误差的单位是″，两者的单位不一致，在计算灵敏度时仅将数值进行灵敏度计算难以保证结果的准确性，该问题值得深入探讨。但本研究认为在灵敏度分析中该问题并不影响分析。此处，以三轴数控机床X向空间误差为例进行说明。由齐次坐标变换得到的X向空间误差模型如式（5）所示。

实际上，式（5）已经过小误差假设简化，即sin（e）≈e，原模型如式（6）所示。式中，角度误差项经三角变换后为常数，然后乘以上一项位置项，因此量纲与平动误差是统一的。

式中，ΔX表示X向空间误差；y表示Y轴运动量；z表示Z轴运动量；δxx表示X轴定位误差；δxy表示Y轴在X方向的直线度误差；δxz表示Z轴在X方向的直线度误差；εyx、εzx分别表示X轴的俯仰和偏摆误差；εyy、εzy分别表示Y轴的滚转和偏摆误差；Sxy、Sxz分别表示X轴与Y轴、Z轴间的垂直度误差。

2 灵敏度分析前需测量全部几何误差导致工作量大

现有研究中，许多灵敏度分析方法需要预先测量出机床全部几何误差，基于误差值才能辨识出关键误差，限制了实际推广与应用。如果已测量出全部几何误差，则直接进行补偿即可，没有必要再进行关键误差辨识，因为灵敏度分析不仅消耗大量计算时间，而且补偿效果也难以等同于补偿全部几何误差。因此，若能在不测量全部几何误差的前提下，仅借助先验知识给出误差的大致分布区间，即可根据灵敏度分析准确计算出关键几何误差，将具有较好的推广与实际应用价值。

目前的灵敏度分析方法中，Sobol法无需提前测量几何误差，仅需确定误差值的分布区间，即可实现灵敏度分析，具有较好的实际应用意义。但是，不同误差分布区间对最终结果准确性的影响需要进一步论证，如何准确给出误差的合理分布区间也值得研究。此外，目前采用Sobol法计算确定样本数均依赖于经验值，不同样本数的选择对灵敏度分析结果准确性的影响尚需论证。

3 五轴数控机床的灵敏度分析未考虑方向误差

不同于三轴机床，五轴机床存在6个自由度的空间误差，即3个位置误差和3个方向误差。尤其在工件精度优化方面，现有的许多灵敏度分析方法仅考虑了3个位置误差，即使是对于复杂曲面工件，也未考虑对方向误差敏感的情况，影响了灵敏度分析的准确性。主要原因为五轴机床几何误差比三轴机床多1倍以上，且同时考虑位置与方向误差，导致灵敏度分析的计算量极大。此外，实际工件的加工精度验证也较少对方向误差进行标定。

Li[43-44]在五轴加工中同时考虑刀尖的位置误差与方向误差，在灵敏度分析中将位置误差分解为由运动轴平移误差与角度误差两部分引起，而方向误差由运动轴角度误差单独引起，从而减小灵敏度分析的计算量并提高准确性，该方法为考虑方向误差的五轴机床灵敏度分析提供了有益借鉴。因此，未来可研究面向五轴机床同时考虑位置与方向误差的灵敏度分析，以及如何减少计算量并实际应用于复杂曲面的方向误差补偿。

4 根据灵敏度系数确定关键误差缺少统一标准

在获得各误差的灵敏度系数后，如何准确确定关键误差的项数，目前暂无统一标准。张根保等[45]根据“80/20”法则确定关键误差，但未明确给出该法则的科学依据。当误差间的灵敏度系数相差较大时，则能简单选取灵敏度较大的误差作为关键误差；但当误差间的灵敏度系数相近时，如何选取关键灵敏度误差，目前尚无标准。现有研究通常按照经验来判别，影响了灵敏度分析的准确性，值得未来研究讨论。

5 关键误差的辨识正确性缺少合理验证方法

目前，许多灵敏度分析方法可用于辨识关键误差，但鲜有合适的方法用于验证结果的准确性。现有验证方法有以下3种： （1）补偿关键几何误差，通过检验补偿的百分比来间接验证。如辨识出5项关键误差并补偿后，运动精度提升80%，说明该5项误差在总误差中占主导作用，但仍难以说明是否还存在第6项关键误差，可能取得更好的补偿效果。（2）计算关键误差的灵敏度系数占总灵敏度的百分比，并将关键误差代入空间误差模型中，检验由上述关键误差引起的误差百分比，若两者相近或后者更高，则间接说明关键误差项辨识准确。但灵敏度分析是基于空间误差模型计算得到的，而用空间误差模型本身进行反向验证，则可能导致科学性不足。（3）不同灵敏度分析方法间进行横向比较，由于灵敏度分析各有优缺点与应用场合，难以用某一种灵敏度分析结果作为参考标准。结合现有验证方法的不足，简便合理的验证方法值得研究。

结论

数控机床是重要的制造业“工作母机”，其精密化研究一直是该领域的研究重点与难点。

近年来，灵敏度分析逐渐成为机床精度优化领域的研究热点，该方法能准确识别对机床精度最敏感的误差参数，对实现高效高精度机床误差补偿具有重要的应用价值。在无需预先测量机床几何误差的前提下，灵敏度分析在同时考虑位置与方向误差、根据灵敏度系数给出关键误差的选取标准以及关键误差辨识准确性的验证等方面具有良好的研究前景，值得未来进一步研究。