伺服系统复合自适应控制研究综述*

朱其新，王嘉祺，谢广明

（1.苏州科技大学，苏州 215009；2.江苏省建筑智慧节能重点实验室，苏州 215009；3.北京大学，北京 100871）

伺服系统（Servo system）又被称为随动系统，主要由控制器、被控对象、检测传感器等基本部分构成，如图1所示。伺服系统属于自动控制系统，同恒值控制系统不同的是，可以通过向系统输入给定信号以及调节控制器参数，保证被控对象的输出信号准确连续地跟随给定信号。因此，跟踪给定信号的快速性和准确性是伺服系统最重要的特点。在先进制造、航空航天和国防军工等重要领域，伺服系统都有着广泛的应用。例如数控机床的进给伺服控制和主轴伺服控制，航天飞行器、运载火箭、雷达的伺服控制，以及火炮、舰船、导弹发射的伺服控制等。

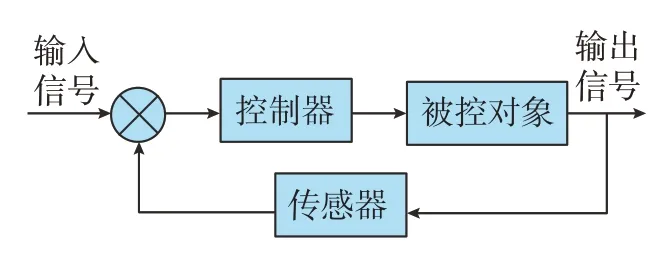
图1 伺服系统基本结构框图Fig.1 Basic structure block diagram of servo system

伺服控制系统可以从多个角度进行分类，根据反馈比较控制方式的不同，可以分为数字比较系统、脉冲比较系统、幅值比较系统、相位比较系统以及全数字系统；根据执行元件的不同，可以分为电液伺服系统和电气伺服系统；根据控制理论的不同，可以分为开环系统、闭环系统以及半闭环系统；根据驱动元件的不同，可以分为直流伺服系统、步进伺服系统以及交流伺服系统。

从伺服系统发展的角度看，国内的发展相较于欧美和日本而言，要滞后许多。20世纪80～90年代，德国、日本等机械制造大国就已纷纷推出拥有自主知识产权的伺服系统，例如西门子、三菱等。而得益于国家对产业升级的大力支持，近几十年来，中国自主的伺服系统研发生产能力已经得到了空前的发展。在未来，伺服系统必然向着高精度、结构简单、高功率密度等方向进一步突破，并逐步优化核心算法，从而满足目前市场巨大的需求量缺口，完成对老旧设备的更新换代，在中高端制造业领域得到更为广泛的发展和应用。

伺服系统的控制理论最早建立在经典控制理论的基础之上，一般是两环或者三环控制系统,控制器设计多为PID（Proportional integral derivative）控制器，参数调节简单方便，因此在实际工程中得到了广泛的应用。但是，伺服系统的特点是被控对象要求跟随输入信号的变化，追求跟随的快速性和准确性。随着工业的发展和控制要求的提高，以及应用场合的变化和系统参数的变化，例如机床中切削力的变化、被控对象增益的变化、负载的变化，都会让参数固定不变的PID控制器不能满足“快速、准确”的需求。更重要的是，PID控制器是典型的线性控制器，而实际的伺服系统包含了大量的非线性因素，如摩擦效应，其基本原理如图2所示。由图3和式（1）可知，摩擦模型是一种多参数的高度非线性模型，而PID控制器无法克服其中的非线性因素。在误差响应曲线中，仅使用PID控制器，存在明显的与摩擦模型相对应的曲线形状，说明PID控制器不能有效克服非线性摩擦效应。因此，在摩擦效应的影响下，伺服系统在速度过零时会出现死区，导致跟随的快速性和准确性降低。

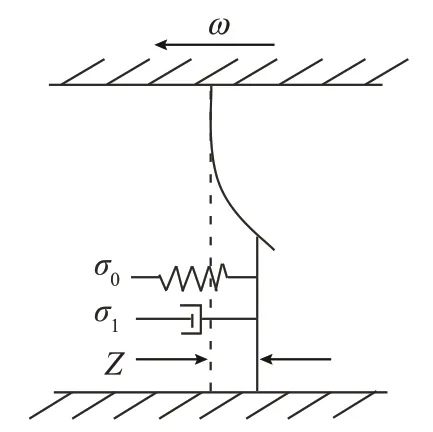
图2 LuGre摩擦模型原理图Fig.2 Schematic diagram of LuGre friction model

图3 正弦信号下的LuGre摩擦效应Fig.3 LuGre friction effect under sinusoidal signal

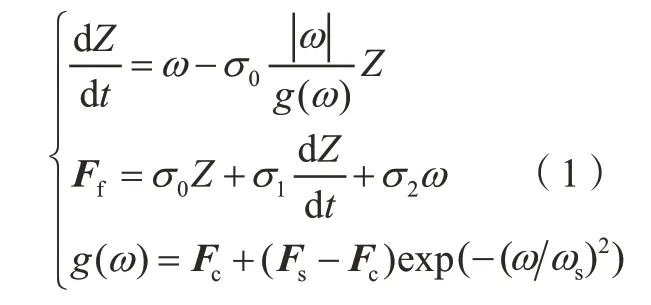
式中，Z为鬃毛的平均变形量；ω为转速；σ0为刚度系数；g(ω)为非线性函数，体现了不同条件下的摩擦效应；Ff为总摩擦力矩；σ1为阻尼系数；σ2为黏滞系数；Fc为库仑摩擦力矩；Fs为静摩擦力；ωs为Stribeck速度；exp()为以自然常数为底的指数运算。

于是，设计人员针对不确定性的伺服系统引入自适应控制，可以根据环境的变化灵活调节自身特性，从而确保在变化的工作环境和系统参数下，都能达到最优的控制效果。其最初的控制方法主要有模型参考自适应[1]、自校正控制等，在判断稳定性方面主要依据李雅普诺夫稳定性理论和波波夫超稳定性理论。其主要应用于航空航天、数控加工[2]、机器人[3]及其他工业领域[4-5]，甚至包括一些非工业领域。

与此同时，一系列其他控制方法，如反推控制、滑模控制、鲁棒控制、模糊控制、神经网络控制、状态观测器、优化算法等，也可以与自适应控制相结合，集中各方法的优点，形成复合自适应控制方法，为未来自适应控制的发展提供了新方向。

传统自适应控制的主要方法

1 模型参考自适应

模型参考自适应方法（MRAC），是指以参考模型作为被控对象的理想模型，比较参考模型和被控对象的输出误差，通过自适应律来实时整定控制器的参数，使误差为0，从而让被控对象的输出满足参考模型的理想输出。麻省理工大学Whitaker教授等于1958年首先利用局部参数最优方法设计自适应律，被称为MIT规则。后来，Butchart等提出使用李雅普诺夫稳定性理论来判断MRAC控制系统的稳定性，从而设计出满足李雅普诺夫稳定性的控制系统。在同一时期，Landau提出使用波波夫超稳定性理论来判断控制系统的稳定性。20世纪80年代以后，随着神经网络及智能控制方法的飞速发展，MRAC控制系统也开始和智能控制方法组合在一起，形成了性能更好的复合控制系统。

以基于李雅普诺夫稳定性理论的模型参考自适应方法为例，如图4所示。其中被控对象的状态方程为：

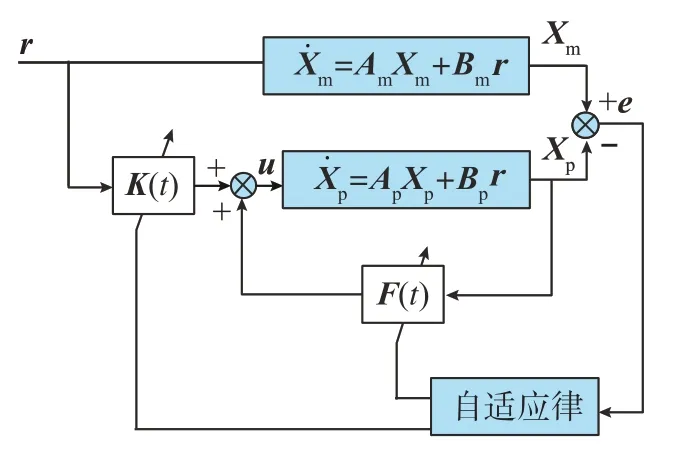
图4 基于李雅普诺夫方法的模型参考自适应Fig.4 Model reference adaptation based on Lyapunov method

其中，Xp为n维状态向量；u(t)为m维控制向量；Ap和Bp分别为n×n和n×m的时变矩阵；K(t)为m×m矩阵，F(t)为m×n矩阵，两者为自适应控制器矩阵，下文中简写为K和F；r为m维输入向量。由图4可知：

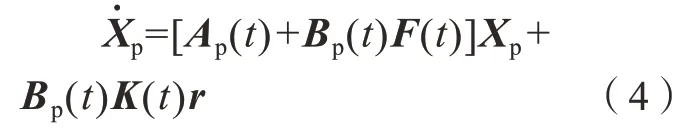
参考模型的状态空间方程为：

其中，Xm、Am、Bm为参考模型的状态向量、状态转移矩阵和控制量系数矩阵。

令误差向量：

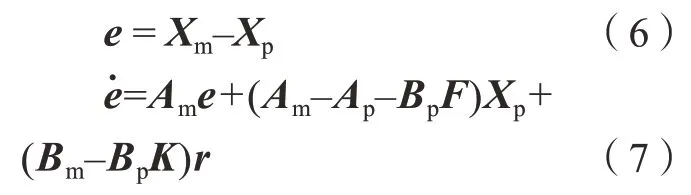
理想状态下，的后两项应该等于0，因此令：

选取李雅普诺夫函数为：

其中，为对称正定矩阵。因为当后两项为0时，正定，所以当时可得自适应律：

在近期的伺服系统研究中，依然有学者采用模型参考自适应的方法来设计控制系统。例如对机械臂[6]、永磁同步电机[7]、非对称液压缸位置伺服系统[8]等被控对象，采用线性化或者非线性参考模型建模，通过自适应控制算法确保系统输出的渐近稳定和跟踪参考输入的零误差。而在惯量辨识方面，Song等[9]基于模型参考自适应系统（MRAS），并结合遗传算法提出了一种新的惯量辨识方法，通过遗传算法来优化自适应增益，从而缩短收敛时间以及提高辨识精度，最终提高永磁同步电机的动态响应特性。

伺服系统模型参考自适应控制的优点是，当出现条件不确定或者扰动的情况，可以通过消除被控对象和参考模型之间的误差，使响应收敛到期望的输出上，控制方法相对简单，稳态精度高，可以避免模型过于复杂所造成的困难。但是模型参考自适应也存在严重的问题，一方面需要事先对被控对象的模型有基本的了解，才能建立合理的参考模型，不适合在模型完全未知或者模型过于复杂的情况下采用。例如，当考虑到伺服系统具有非线性摩擦效应时，由于摩擦模型是一个典型的高度非线性模型，公式十分复杂，参数较多，难以采用简单的参考模型来代替，这给自适应控制器设计带来了困难。另一方面，在实际工程应用中伺服系统的被控对象数学模型并不是不变的。例如永磁同步电机的负载发生变化、转动惯量或质量发生变化；电机长期工作磨损，摩擦系数也会发生变化，由此会导致电机传递函数的参数发生变化。如果此时还采用固定的参考模型，那么自适应控制器参数就会不符合当前的工作情况，严重影响伺服系统跟随时的快速性和准确性。为此，需要设计更为复杂的复合自适应控制算法才能进一步克服模型参考自适应的不足。

2 自校正控制

自校正控制的思想最早于1958年由Kalman提出。1973年，瑞典隆德工学院的Wittenmark提出了最小方差自校正调节器。该方法实现简单，经济实用，但是缺少工程约束，功能单一。1975年，英国牛津大学的Clark和Gawthrop提出了广义最小方差自校正控制器，克服了过去自校正控制器的主要缺点。随即在1976年，英国剑桥大学的Edmunds基于次最优设计思想，提出了极点配置自校正控制技术。20世纪80年代以后，随着神经网络的快速发展，以及在高度非线性和严重不确定系统控制方面的优势，各国学者开始重点研究基于神经网络的自校正控制器设计，自校正控制的基本原理如图5所示（u(t)为控制量，y(t)为被控对象实际输出，θ^是参数估计器输出的参数估计值）。

图5 自校正控制基本原理图Fig.5 Basic principle diagram of self-tuning control

近年来，在对自校正控制的研究中，有非常多的成果是和模糊控制相结合的，其中较为常见的是模糊自校正PID控制[10-11]，有效解决了数学模型高度非线性以及不精确时的自校正问题。除此之外，自校正控制还与参数辨识相结合，通过参数辨识为自校正控制提供精确的模型参数。龙国浩等[12]针对根据波波夫超稳定性理论设计离散系统模型，通过辨识转动惯量并分析其与速度环参数的关系，得到自校正规律。王飞[13]基于遗忘因子递推最小二乘的自校正算法，实现了运动伺服系统前馈控制器参数的自我校正。余同应[14]提出在对电机伺服系统主动子、次动子辨识的参数完全收敛的条件下，通过极点配置实现自校正控制。

当然，自校正控制也有待改善的方面。自校正控制的前提是精确的参数识别，所以需要收敛速度更快、精度更高的辨识方法，如在永磁同步电机中，可能需要通过输入激励信号来实现参数辨识，但这会干扰到伺服系统的正常运行，而且如果出现参数识别速度过慢的情况，伺服系统就无法快速且准确地跟踪到给定信号，导致跟踪性能降低。同时，当伺服系统存在较强的不确定性和干扰时，自校正控制的有效性和稳定性也有待论证和提高。因此，相关学者逐步采用复合自适应算法来克服自校正控制的不足。

伺服系统复合自适应控制的主要方法

伺服系统对变化的给定信号的跟踪要求具有快速性和准确性，但是该系统存在模型高度非线性、数学模型参数变化、参数辨识困难、鲁棒抗扰性差等问题，传统的模型参考自适应和自校正控制无法有效克服上述问题。近年来，众多学者针对伺服系统采用复合自适应控制，如自适应反推控制、自适应神经网络控制、自适应鲁棒控制、自适应观测器控制、自适应模糊控制、自适应滑模控制、自适应优化算法控制，以及一些其他的复合自适应控制，从而达到克服非线性效应、快速精确识别数学模型参数和提高鲁棒抗扰性的效果。

1 自适应反推控制

20世纪70年代，Morse等首先提出了反推控制的思想用来处理高阶自适应控制的问题。到了90年代，自适应反推控制再次受到学术界的关注。当时的学者通过自适应反推控制，实现了基于李雅普诺夫函数的单变量非线性闭环系统对输入信号的渐近跟踪。随着此后自适应反推控制的发展，逐渐被广泛应用于电机、机器人等工业领域。

反推控制的基本原理是，在不需要硬件的情况下，通过计算得到一连串“虚拟”的信号。再通过递归，每一步处理一个简单的误差系统，从而得到最终的控制信号，如图6所示。这样的控制信号可以灵活选择，能有效改善控制系统的性能。

图6中u为最终控制信号，αi为虚拟控制信号，τi为调参律。其中控制器的设计过程如式（14）所示。

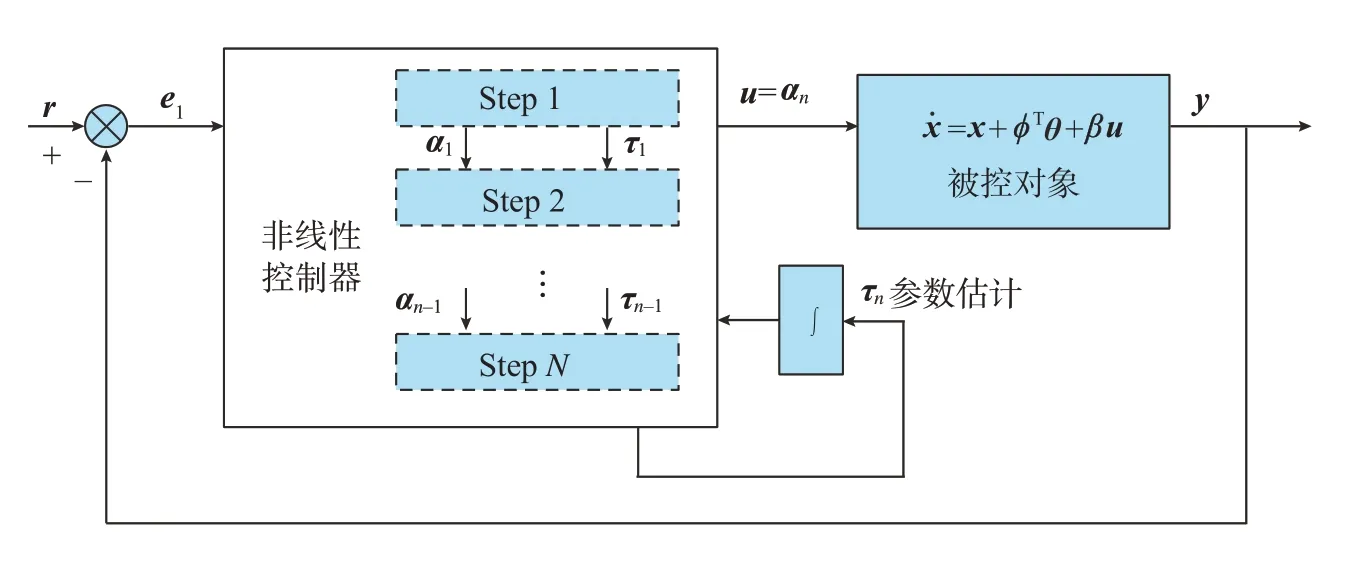
图6 自适应反推控制示意图Fig.6 Schematic diagram of adaptive backstepping control

其中，φi和β为状态量之间的函数关系。定义误差e1=r-x1，此处一般情况下设计为y=x1，通过虚拟控制量(x2)d得出而参数θi则通过自适应算法求得，其中包括α1(x1)=(x2)d和=τ(x1)。第一步的反推完成后，再定义误差e2=(x2)d-x2，通过虚拟控制量(x3)d得出。以此类推，最后反推出最终控制量u=αn。

基于自适应反推控制具有设计简单、易于工程实现等优点，因此该算法得到了广泛的应用。文献[15-17]针对非线性系统设计自适应反推控制器，分别确保了参数不确定系统的全局有界跟踪、克服了约束输入问题以及消除了柔性伺服系统的复杂性。Zhao等[18]提出一种将投影算法与反推控制相结合的自适应算法，减小了间隙非线性对双电机驱动伺服系统的影响。Lin等[19]提出了一种基于自适应递归神经网络不确定性观测器的积分反推控制器，可以估计伺服系统控制所需的集中不确定性。

由于伺服系统的控制环节较多，可以采用自适应反推控制与滑模控制相结合。其中自适应反推控制参数少且调节简单，可以有效降低滑模控制的复杂度。Chen等[20]提出一种反推滑模控制器，同时利用自适应径向基函数网络对不确定性进行估计，可以克服系统的不确定性影响。Tran等[21]则针对电液机械手和电液伺服系统中的匹配和非匹配不确定性问题，设计出一个基于自适应滑模和自适应非线性PI结构的反推方案。

伺服系统在运行过程中存在Stribeck摩擦效应，该效应显示出强烈的非线性，使电机转速出现脉动现象。而自适应反推控制在处理非线性等特殊结构上具有显著优势，与摩擦模型相结合时不需要精确的摩擦参数，适用于摩擦力矩补偿。文献[22]和[23]针对光电伺服跟踪系统设计了一种自适应反推摩擦补偿控制器，实现了非线性摩擦下的精确控制，并减小了外部干扰的影响。Zhao等[24]基于摩擦参数的模糊辨识设计了一种自适应反推控制器，具有更好的跟踪性能和鲁棒性。

为了更好地发挥自适应反推控制的优点，近年来也有学者在自适应反推控制的基础上，引入非线性阻尼项补偿死区非线性的不确定性[25]，引入神经网络加快收敛速度[26]以及与优化算法结合整定最优参数[27-28]。总体上说，在伺服系统中引入自适应反推控制，可以将伺服系统的多个环节分解为多个子系统，达到调节参数少、易于工程实现的目的。该方法主要针对克服伺服系统的非线性和参数不确定性问题，自适应控制可以估计不确定参数，反推控制可以简化非线性控制的复杂度，提高系统的跟踪性能、鲁棒性和抗干扰性。但是反推控制也存在明显的不足，如依赖精确的数学模型，当参数受到扰动而发生变化时，性能也会受到影响。同时由于设计虚拟控制量需要大量求导，也会出现“微分爆炸”现象。

2 自适应神经网络控制

神经网络起源于1943年数理逻辑学家Pitts和McCulloch所建立的MP模型，在该模型中单个神经元初步具有执行逻辑运算的功能。1949年Hebb提出神经网络学习思想，1957年Rosenblatt提出了感知器模型及其算法。神经网络虽然在20世纪70年代遭遇衰退，但是80年代迎来了复苏，1986年BP算法被提出，2006年深度学习的思想被提出，2016年的AlphaGo更是把深度学习推向新的高度。

神经网络控制是近年非常热门的智能控制方法，通过模仿人脑的工作原理，由大量的神经元组成网络，拥有强大的自学能力。将神经网络引入自适应控制中，可以大大提高控制系统的性能，其基本原理结构如图7所示。

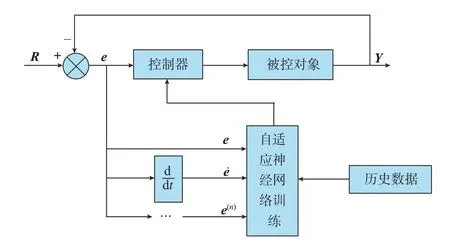
图7 自适应神经网络控制结构示意图Fig.7 Structure diagram of adaptive neural network control

以自适应线性神经网络的梯度法为例，定义目标函数J(ω)为和方差公式（欧几里得距离）。其中，y(i)为实际输出，为线性激活函数。

神经元的更新律为：

式中，w：为更新后的权重；w为更新前的权重；Δw为权重增加值，η为学习速率，可采用随时间变化的自适应学习率，确保进一步趋近于全局最优解。

自适应神经网络在伺服系统中有着广泛的应用。Dos Santos等[29]采用自适应神经网络，通过在线学习更新神经网络的权值向量，优化了电液伺服执行器的精确位置跟踪性能。Lv等[30]提出了一种基于强化学习的自适应动态规划算法来近似最优稳定输入，该方法采用三层神经网络辨识未知伺服机构，利用自适应梯度法来调整神经网络权值，实现收敛和最优。Tao等[31]提出一种采用径向基函数神经网络和自适应算法的方法，对空间转台中电缆束干扰进行估计。该方法不需要进行建模，减小了对干扰进行补偿的复杂性。

伺服系统在实际运行中往往会受到外部扰动的影响，传统方法是采用鲁棒控制来提高系统的抗干扰能力。而由于自适应神经网络控制具有针对非线性和不确定性对象的自学习能力，因此，文献[32-34]采用自适应神经网络与鲁棒控制相结合的方法，在伺服系统参数不确定的情况下进一步优化鲁棒控制器，补偿外部扰动等因素带来的参数不确定。

自适应神经网络具有并行性、自然容错性等特点，在处理非线性动态系统时有着理想的控制效果。例如伺服系统的摩擦效应就是典型的非线性问题，尤其是摩擦参数不确定时，传统的方法是采用普通的观测器估计。Na等[35]提出一种基于估计误差驱动的学习策略的非线性伺服系统自适应控制，通过一种新的摩擦模型的增广神经网络，使跟踪误差和参数估计同时收敛。而文献[36]和[37]采用自适应神经网络与观测器结合，不仅能在摩擦参数不确定的情况下克服参数估计的问题，还能发挥出对非线性系统控制的优势，补偿摩擦效应。

除此以外，自适应神经网络还有其他应用和研究成果。文献[38-42]都采用自适应模糊神经网络，通过将输入层和输出层模糊化，使得自适应神经网络控制可以充分利用模糊控制的经验知识，进一步提高自学习自适应能力。文献[43-44]在PID控制的基础上引入自适应神经网络，自动匹配电机运行参数和调整控制器参数，减小位置和速度误差。Lin[45]提出一种新的自适应递归Legendre神经网络控制系统，兼具自适应律递归Legendre神经网络控制和估计律报酬控制的优点。

总而言之，自适应神经网络控制主要针对伺服系统的非线性控制问题，如非线性摩擦效应。该方法可以提高估计参数的收敛速度，解决参数不确定的问题，将非常复杂的非线性问题的难度大大降低，从而提高伺服系统的跟踪速度和稳态精度。但是有些自适应神经网络需要大量数据进行训练，无形中增加了工作量，降低了前期的收敛速度。

3 自适应鲁棒控制

鲁棒性是指控制系统在参数受到摄动的情况下，能够保持某一种性能的特性。将闭环控制系统的鲁棒性作为设计目标时，该控制器被称为鲁棒控制器。而在自适应控制中，也可以通过引入鲁棒控制来结合两者的优点。

鲁棒控制最早在1927年被Black提出，利用反馈和大环增益来设计电子管的不确定性变化。1932年Nyquist提出了动态稳定性与大环增益之间的权衡，与Black的概念共同组成了鲁棒控制设计的基础。到了20世纪60～70年代，鲁棒控制进入状态变量时期。其中1964年Cruz和Perkin提出MIMO系统的灵敏度矩阵，将SISO系统的灵敏度结果向MIMO进行了推广。80年代之后，研究人员将鲁棒控制应用于不确定性被控对象的研究中，诞生了大量的寻求适应大范围不确定性分析的理论和方法，自适应鲁棒控制结构示意如图8所示。

图8 自适应鲁棒控制结构示意图Fig.8 Structure diagram of adaptive robust control

伺服系统是一种不确定非线性系统，针对单纯的参数不确定，只需要采用自适应控制就能消除跟踪误差。但是当系统中同时包括参数不确定和干扰不确定时，鲁棒控制与自适应控制相结合就能同时消除两种不确定性对系统的影响。文献[46-49]在自适应控制中引入鲁棒控制，当存在状态和输入约束的不确定、参数不确定以及干扰不确定时，能确保稳定和精确跟踪，减少不确定性带来的负面影响。在伺服系统中，还有典型的非线性问题就是非线性摩擦效应，因此同样可以采用自适应鲁棒控制来克服摩擦效应问题。文献[23]和[37]是将摩擦模型与自适应鲁棒控制相结合，减小摩擦与外界干扰的影响，解决参数不确定、参数估计误差和摩擦补偿误差等不确定性问题。

除了以上的研究成果，Liu等[50]提出了针对PWM三相永磁无刷直流电动机的鲁棒自适应模糊控制器，确保跟踪性能和鲁棒性能。Xin等[51]提出一种鲁棒滑模控制器，采用自适应算法估计滑模切换项的增益，与鲁棒控制相结合确保伺服系统位置环的静态精度和动态跟踪性能。这些方法也体现了近年来自适应鲁棒控制的发展趋势，在原有方法的基础上引入更多的控制方法，进一步改善了伺服系统的跟踪性能和鲁棒性。

综上所述，自适应鲁棒控制既包含了自适应控制实时动态调节参数的优点，同时也包含了鲁棒控制在受到摄动的情况下能够保持系统性能的优点。该方法主要针对的问题是，当伺服系统面临参数不确定、参数估计误差以及多种干扰的情况下，保证自适应系统的稳定性和抗干扰能力，确保动态跟踪性能。但是，由于鲁棒控制系统一般不工作在最优状态，因此伺服系统的稳态精度略差。目前鲁棒控制方法中最热门的H∞控制存在的普遍问题是控制器的阶数偏高，应用在伺服系统上过于复杂，这也成为了自适应鲁棒控制需要改进的一个方向。

4 自适应观测器

状态观测器是指根据系统的输入量和输出量来估计状态变量的一种动态系统。状态观测器不仅发展出了状态反馈等一系列技术，而且在实际控制工程中发挥着重要作用。

状态观测器最早于20世纪60年代由斯坦福大学Luenberger提出。然后向非线性系统进行推广，设计出KKL观测器。到了1992年，高增益观测器首次应用于非线性系统状态估计中。在随后的发展过程中，该观测器衍生出了两个学派——法国学派和美国学派。其中法国学派主要研究全局Lipschitz条件下的全局估计，而美国学派则以密西根州立大学的团队为主。

以如下非线性系统为例：

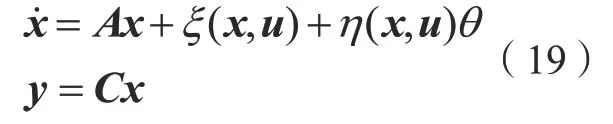
其中，x、y、u分别是系统的状态向量、输出向量和输入向量；ξ、η分别为非线性函数；θ为系统未知参数。对模型设计如下自适应观测器：

式中，是系统状态估计是θ的估计值；L是观测器的增益矩阵。根据假设条件，设β和σ为正常数，Q为正定矩阵，g(,u)为非线性项，可以令：

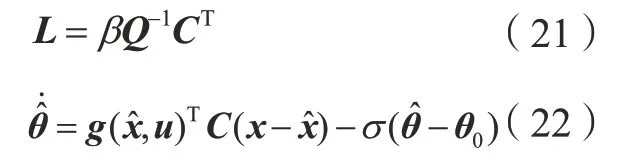
因此，取李雅普诺夫函数：

由此可得该观测器是渐近稳定的。其结构原理如图9所示。

图9 自适应观测器结构原理图Fig.9 Schematic diagram of adaptive observer structure

当伺服系统出现参数不确定等情况时，可以将观测器引入自适应控制中。观测器可以对特定状态、外界扰动等各个方面进行在线估计观测，而自适应控制可以根据观测器的估计值调节控制器参数，从而克服伺服系统的参数不确定问题。文献[52-58]针对存在大量建模不确定性的非线性伺服系统，采用多种不同的自适应观测器，实现了对不可测系统状态、不确定参数、未知干扰的观测估计，确保观测系统的收敛速度，提高了伺服系统补偿控制和给定信号跟踪的精度。

在高精度伺服系统中，非线性摩擦对系统的动态以及静态性能影响很大，容易出现低速爬行现象和速度过零的畸变现象。然而在通常情况下，摩擦模型参数是未知的。尤其是当前应用最为广泛的LuGre摩擦模型，存在包括静态参数和动态参数在内的7个未知量。为了准确辨识摩擦参数，传统的方式有“Stribeck曲线拟合法”和“微阶跃响应法”。这些方法使用复杂且不能实现运行过程中的实时辨识。因此，文献[59-62]针对伺服系统摩擦现象，设计摩擦模型参数的自适应观测器进行估计，从而克服不确定性，实现精确的摩擦补偿，确保伺服系统信号跟踪的快速性和准确性。

综上所述，在自适应控制中引入观测器，可以帮助伺服系统估计不确定参数、未知扰动以及未知状态，从而让自适应控制系统拥有更好的控制精度以及稳定性。尤其是针对伺服系统非线性摩擦效应进行补偿控制时，观测器可以用来观测摩擦状态变量及模型参数，确保自适应控制器的跟踪精度和鲁棒性。当然，观测器也有使用范围，当电机负载和惯量等参数变化速度大于收敛速度时，观测器就无法及时收敛到相对应的结果上了。因此，提高自适应观测器的收敛速度和精度是今后进一步改进的重要方向。

5 自适应模糊控制

模糊控制的基础是模糊数学。在经典控制理论中，系统模型越精确，控制系统的性能就越好。但是，实际的伺服系统都是非常复杂的，相关因素太多。相关因素中不仅有未知参数和未知扰动，还有高度非线性的摩擦效应。所以研究人员便尝试通过模糊控制等一系列智能控制的方法来解决控制问题。

1965年美国专家Zadeh提出模糊集合描述不确定性信息；1974年英国Mamdani在蒸汽发动机上运用了模糊控制；1985年日本在家电上实现了模糊控制的实用化。进入21世纪，模糊控制更是应用到了触控系统、模式识别等更广阔的领域。

将模糊控制引入自适应控制系统中，也是非常常见且有效的方法，如图10所示。

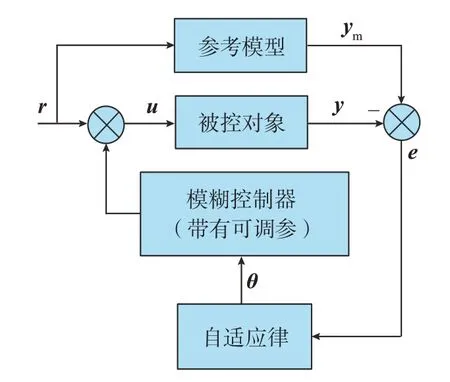
图10 自适应模糊控制原理图Fig.10 Schematic diagram of adaptive fuzzy control

伺服系统工程实践中，PID是一种经典的控制方法，但其响应曲线容易发生超调，控制精度低。所以研究人员将自适应模糊控制应用于PID控制中，根据专家的知识经验和反馈误差实时调节控制参数，实现更快的响应速度和更高的控制精度。Wang等[63]开发出了一种模糊自适应PID控制器伺服电机控制系统，有效处理了非线性和不确定性问题。文献[64-66]采用自适应模糊PID控制算法，将其应用于液压伺服缸位置控制中。由此可见，自适应模糊PID控制算法在线整定参数，克服了经典PID控制器不能应用于不同场合的缺点。

近年来，很多方法被应用到自适应模糊控制当中。由于自适应模糊控制不需要精确的数学模型，在针对参数不确定、负载未知的非线性伺服系统时，该方法可以将控制算法模糊化，有利于其他不同方法在复杂环境下的运用与改进。Precup等[67]设计了一种自适应混合粒子群优化算法，即引力搜索算法，将其应用于模糊控制器的优化整定中，降低了参数的灵敏度。Cerman等[68]在经典滑模自适应控制的基础上引入模糊自校正机制，减少了常见的抖振问题。El-Sousy[69]提出基于滑模辅助控制器和递归径向基函数的自适应模糊神经网络，能够控制更大程度的范围不确定性。Huang等[70]针对液压机械手系统，提出一种间接自适应模糊滑模控制，采用自适应算法和模糊逼近原理对未知参数进行估计，并对滑模控制器切换项进行模糊逼近，有效抑制了抖振和干扰。文献[71-72]采用自适应模糊逻辑系统，分别实现了模型参考自适应的调整和伺服系统对非线性的在线逼近。同样以伺服系统摩擦效应为例，文献[24]中的摩擦伺服系统非线性部分就是用自适应模糊逻辑系统进行逼近，克服了参数未知和负载转矩未知的情况。

综上所述，自适应模糊控制较为常见的应用就是PID控制器参数的自整定，但并不仅限于此。在伺服系统控制应用中，自适应模糊控制能够克服参数不确定、负载转矩未知等复杂问题，并对其进行逼近和估计，从而保证伺服系统跟踪的快速性和准确性。例如遇到非线性摩擦问题时，就可以采用自适应模糊控制，既能估计摩擦模型参数，又能克服其非线性。但是模糊控制毕竟是模仿熟练人员的丰富经验，所以需要大量的实践经验作为控制基础，信息简单的模糊控制只会降低控制精度和动态性能，这也是自适应模糊控制亟需解决的问题。

6 自适应滑模控制

滑模控制的本质是一种非线性变结构控制方式。根据系统当前的状态，控制器就会使系统沿着滑动模态的轨迹运动。因为滑模控制的设计与系统参数和扰动无关，所以可以克服参数不确定性、未知干扰等问题。当然，滑模控制也是有缺点的，那就是在切换控制的过程中，容易发生抖振现象。

滑模变结构控制最早在20世纪中期由苏联学者提出，起初主要以SISO定常或时变系统为主。到了60年代后期，研究对象逐步扩展到线性MIMO系统以及非线性系统。70年代开始受到广泛关注，经过几十年的发展形成了自己的体系。80年代以后，滑模变结构控制受到微分几何的影响，出现了基于精确输入-状态、输入-输出线性化和高阶滑模控制等新方法。如今，滑模控制广泛应用于概率分布参数系统、离散系统、不匹配不确定性系统、机器人、电机拖动系统等。

如图11所示，被控对象系统的数学模型可表示为：

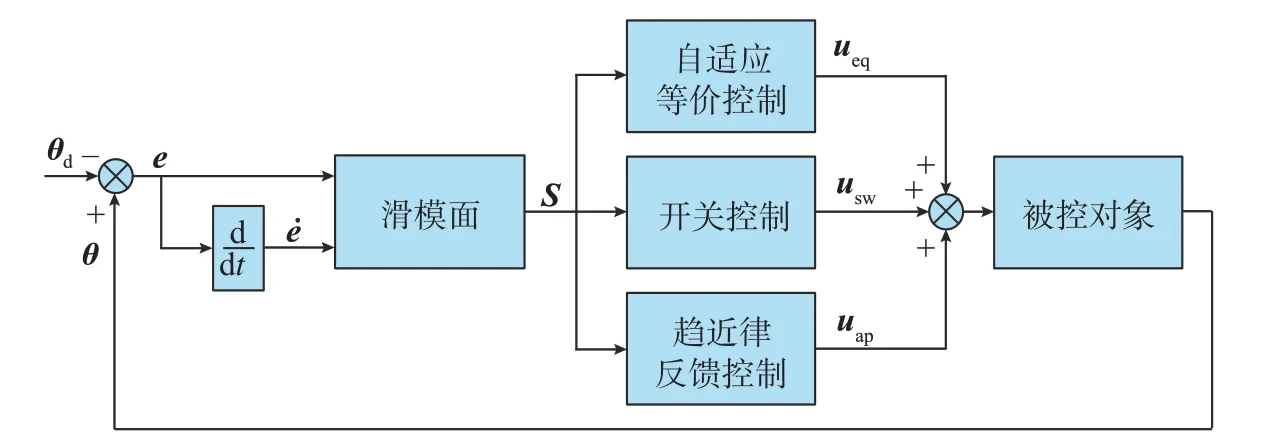
图11 自适应滑模控制原理图Fig.11 Schematic diagram of adaptive sliding mode control

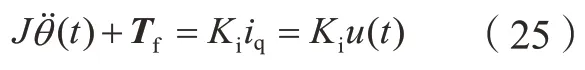
其中，J为转动惯量；θ为位置输出；Tf为负载转矩；Ki为转矩系数；iq为q轴电流；u为控制量。所以令位置误差e(t)=θ(t)-θd(t)，θd(t)为参考位置输入，λ是滑模面的参数，定义线性滑模面s(t)为：

控制器设计为：

其中，定义ueq(t)为自适应等价控制；usw(t)为开关控制；uap(t)为趋近律反馈控制。根据等价控制的定义，可得：

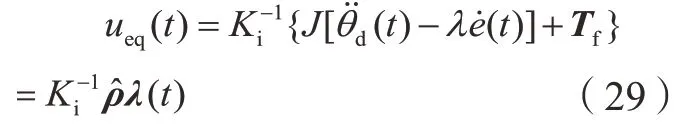
其中，η为开关增益系数；φ为边界层宽度；sat(s,φ)为饱和函数。

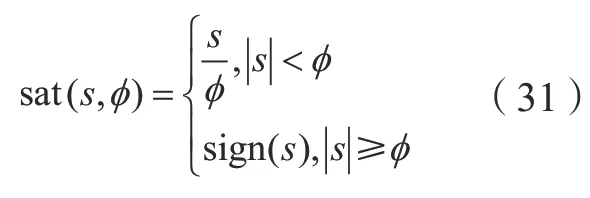
趋近律反馈控制设计为：

其中，k＞0，为趋近速率。所以控制率表示为：

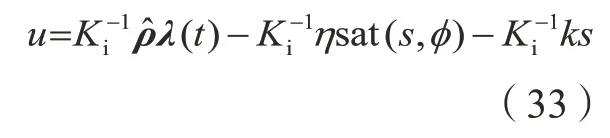
在滑模控制器设计完成后，在自适应控制律引入参数向量估计值

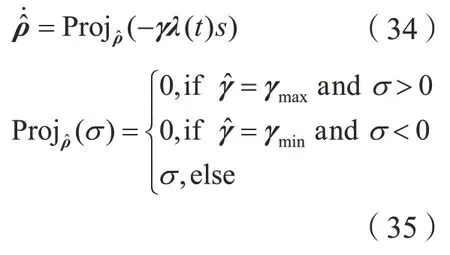
其中，γ=diag(γ1,γ2)是自适应增益矩阵。

自适应滑模控制中，滑模面的收敛和抖振问题是非常重要的。因为由式（34）可知，自适应律和滑模面有关，滑模面的收敛速度将直接影响到自适应律的调节速度。为此，Zhang等[73]提出了一种引入指数趋近律和幂趋近律的自适应滑模控制器，能够缩短到达滑模面的时间，并且减小滑模变结构的抖振问题。

由于建模误差、机械运行时的磨损、测量误差以及非线性，伺服系统的参数实际上是不确定的。因此，众多学者采用自适应控制来估计不确定的参数，从而灵活调整控制参数。而滑模控制也具有设计简洁、响应速度快和鲁棒性强的特点，与自适应控制相结合，能够进一步保证非线性系统在参数不确定的情况下的收敛性，以及对输入信号的实时稳定跟踪。Nie等[74]采用自适应算法对系统的不确定参数进行估计，并通过该算法调节开关函数，避免滑模控制器的抖振问题。Wang等[75]则提出一种基于自适应非奇异终端滑模控制的参数估计方法，通过自适应观测器估计未测量状态变量，再通过滑模控制器实现高性能的跟踪控制。文献[76]和[77]针对系统的不确定性，采用了自适应模糊滑模控制器，有效改善抗干扰能力。Cerman等[68]引入模糊自校正机制对滑模控制参数、扩展反馈和切换增益进行自适应控制。Zhang等[78]采用双观测器估计不可测摩擦状态，并采用自适应滑模控制律进行摩擦补偿。Kayacan等[79]提出一种基于2型模糊三角隶属函数神经网络训练的滑模控制算法，有效地克服了电液伺服系统的非线性问题。

除上述几个方面，自适应滑模控制还有其他的应用场合。文献[80-83]分别采用模糊神经网络遗传滑模、自适应PI滑动面、模糊决策器和正交Haar小波变换，有效抑制了自适应滑模控制的抖振问题。文献[84]针对感应伺服马达驱动系统进行对比，证明基于估计器的自适应滑模控制比传统的滑模控制性能更佳。Jiao等[85]提出了一种基于遗传算法优化的自适应滑模位置控制器，可以估计扰动系统中未知扰动的大小，然后通过遗传算法对自适应滑模控制器的参数进行优化。Wang等[86]提出一种改进的自适应漏斗控制方法，设计辅助滤波运算来提取参数估计误差的信息，作为参数更新律中的新泄漏项，然后在自适应律中引入滑模技术，实现有限时间收敛。

综上所述，自适应滑模控制主要针对伺服系统的非线性和参数不确定问题。合理的滑模面和趋近律可以有效提高伺服系统的跟踪精度，因此自适应滑模控制具有响应速度快、抗扰能力强、鲁棒性好及控制率整定方法简单等优点。但是，滑模控制容易抖振的缺点依然要考虑进去。所以在设计自适应滑模控制的过程中，要通过改进对滑模控制器增益的自适应律，来减小其抖振现象，改善控制器的性能。

7 自适应优化算法

智能优化算法主要包括遗传算法、群智能优化算法等多种算法。其中，出现较早的是模拟退火算法，于1953年由Metropolis提出，随后于1983年被Kirkpatrick应用于组合优化。遗传算法是由美国密歇根大学Holland教授于1975年首先提出。群优化算法出现相对较晚，可以被看作是个体与个体或环境之间的互相作用，最终整体上形成的一种智能行为。受到真实蚁群行为研究的启发，意大利学者Dorigo于1991年提出人工蚁群算法。而粒子群优化算法则是模拟鸟群觅食行为后发展出来的一种基于群体协作的随机搜索算法，于1995年由Kenney和Eberhart提出。

在自适应控制中引入智能优化算法，可以大大提高参数估计的收敛速度及系统的跟踪精度，并且计算成本低、性能好。其基本结构原理图如图12所示。

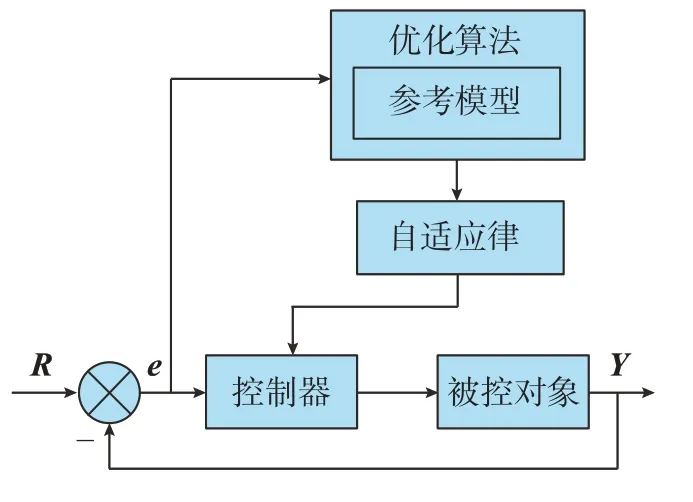
图12 自适应优化算法基本结构原理图Fig.12 Basic structure diagram of adaptive optimization algorithm

传统的PID控制器参数整定采用人工经验，很难得到理想的最优值。因此，不少学者都采用自适应优化算法来整定PID控制器参数，该方法灵活、简单、易理解，在解决伺服系统控制的实际问题有着广阔的前景。Liu等[87]提出一种改进细菌觅食优化算法，引入非线性自适应步长来平衡全局和局部的搜索能力，提高了PID参数整定的精度。Essa等[88]也将自适应加权粒子群算法引入到液压位置控制系统的PID参数整定中。文献[89-90]分别采用多目标遗传算法和基于增益相位裕度遗传算法对PID控制器参数进行整定。

自适应优化算法除了能够整定PID控制器参数，还可以用来整定滑模控制、反推控制和模糊控制。通过自适应优化算法，可以优化滑模控制器的自适应参数和开关控制参数，克服反推控制中的不确定项和负载扰动，优化模糊控制系统的隶属函数和控制规则。文献[85]中，研究人员利用自适应遗传算法对滑模控制的自适应参数和开关参数进行优化。文献[27-28]中，研究人员都是在自适应反推控制器中引入粒子群优化算法，通过优化算法调整自适应控制器的参数。文献[38、67、91]中，研究人员分别在自适应模糊控制器中引入粒子群优化算法或者遗传算法，可以使自适应模糊控制器的灵敏度降低，改善自适应能力和学习速率，对非线性系统进行精确控制。

除了上述的PID控制器参数整定和滑模、反推、模糊控制器整定，自适应优化算法还有其他的应用场合，如系统参数辨识。伺服系统参数的实时获取是实现高性能控制和可靠状态监测的前提，可是动态模型的非线性、多参数、强耦合等特点给参数辨识带来了困难。因此，众多学者都选择将自适应优化算法引入参数辨识。自适应优化算法在搜索的过程中对于待辨识的系统基本没有限制，不要求参数空间的连续性和可导性，在全局都具有良好的寻优能力。文献[9]中，研究人员基于模型参考自适应引入遗传算法，加快了惯量辨识的收敛速度，提高了辨识的精度以便实现控制参数的在线优化。Du等[92]提出采用自适应的遗传算法对无人直升机模型进行辨识，并根据辨识结果设计补偿器。

综上所述，智能优化算法主要分为遗传算法和群智能优化算法，其中粒子群优化算法应用较为广泛。优化算法常常要与其他控制方法相结合，协助其他方法用更快的速度和更短的收敛时间来调整伺服系统的控制参数，从而达到更准确的控制精度和更快速的跟踪性能。但是其缺点在于非常依赖初始参数的选择，否则会出现计算量大、收敛速度慢的现象，最终陷入局部最优，出现“早熟”现象。

8 复合自适应控制方法

复合自适应各控制方法的优缺点如表1所示。复合自适应控制的方法是多种多样的，除了上文归纳的几大类，其实还有很多其他类型控制方法，例如基于快速傅里叶变换和力脉动估计的自适应前馈抑制控制[93]、全形式动态线性化的五模型自适应控制[94]等。总结起来，这些方法主要都是针对伺服系统的参数不确定、外部扰动、参数和扰动的估计、摩擦以及系统非线性的问题。不同的方法与自适应控制相结合，可以将各自的优点引入到自适应控制器中，从而可以改善控制精度、跟踪速度、鲁棒性、抗干扰能力等，满足伺服系统高精度、高效率、高稳定的控制要求。

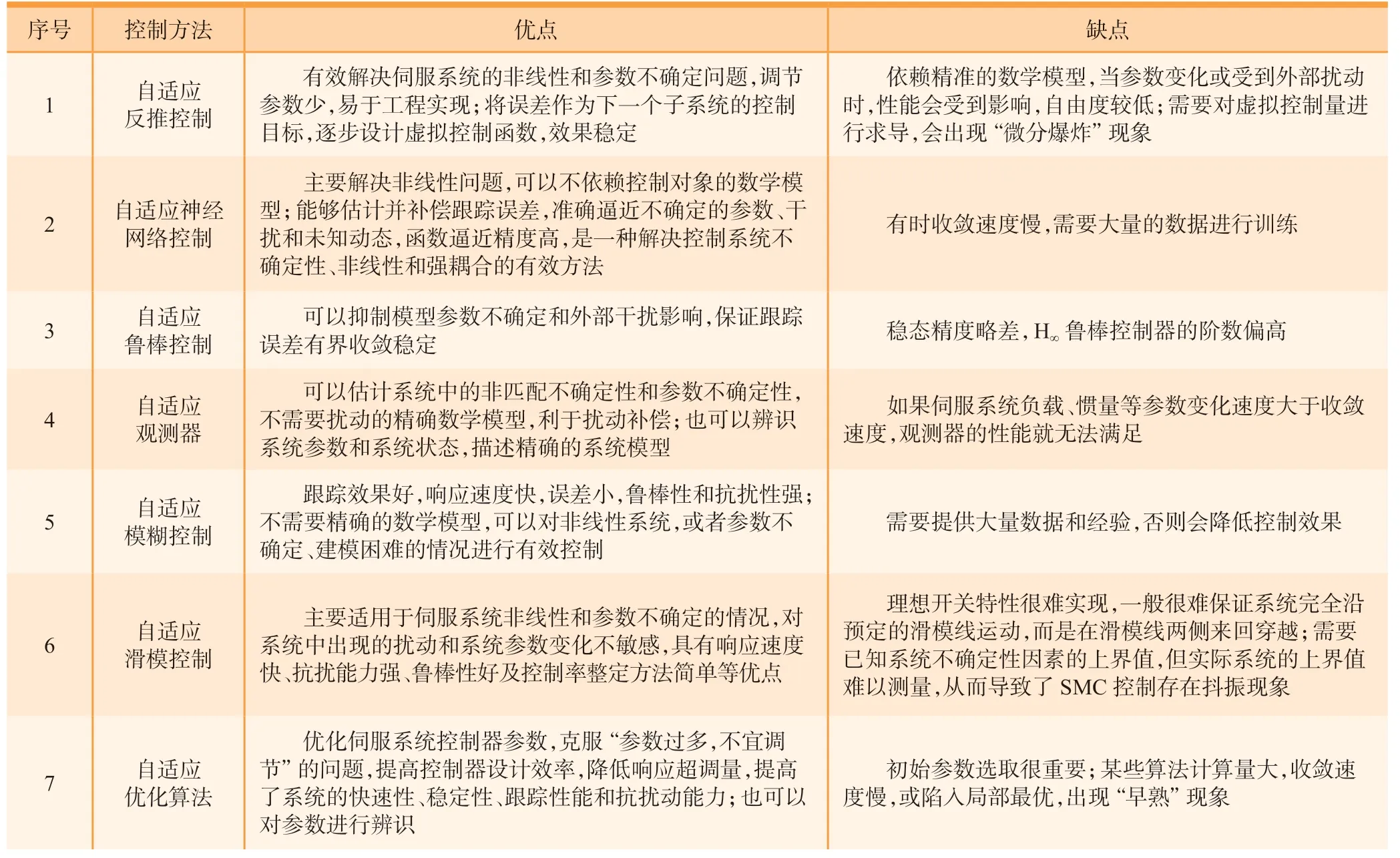
表1 伺服系统复合自适应控制方法Table 1 Composite adaptive control methods of servo system

伺服系统自适应控制的主要问题与发展方向

伺服系统复合自适应控制在发展的过程中，尚存在一些未解决的问题，总结如下。

（1）当自适应控制中引入算法时，算法的初始参数往往是人为选择的。初始参数选择的好坏，将直接影响到算法的性能以及收敛的效果。

（2）采用智能算法等方法对系统进行参数估计时，估计值的收敛需要一定时间。因此在实际工程的应用中，如果估计值的收敛时间过长则失去其本来的应用价值。

（3）实际工程中的系统往往都是非线性的，这些非线性因素包括摩擦、间隙等，且在系统中必然存在参数变化和外部扰动等不确定性问题。但是，为了研究问题的简便，现有的研究成果一般只考虑其中一部分因素，而忽略了另外一部分因素。

（4）复合自适应控制结合了各种控制方法的优点，但是同时也存在不同方法自身的缺点。例如引入滑模控制后必须要考虑本身的抖振问题；采用反推控制要考虑“微分爆炸”问题。因此控制越复杂，性能越好，但是需要考虑的问题也越多。

针对以上的问题，伺服系统复合自适应控制在今后需要发展的方向包括以下4个方面。

（1）算法的初始参数的确定方法研究。采用更加优化的算法来估计和提供初始参数，以保证算法的收敛性。

（2）参数估计的优化算法研究。采用更加优化的算法来估计相关参数，以保证参数估计算法的收敛速度。

（3）新的复合自适应控制方法的研究。能够实现对参数不确定、外部干扰、间隙非线性和摩擦非线性补偿等问题的同时控制。开发能够消除多种干扰的先进算法，让一个控制系统能够满足更多方面的要求，以提高伺服系统精度。

（4）不同算法的结合方法研究。考虑到各个方法各有优点和不足，通过不同方法之间的互补，从而保证该复合自适应控制的总体性能能够达到最优。

结论

本研究以伺服系统为例，介绍了复合自适应控制的多种方法。传统意义上的自适应控制主要分为两类：模型参考自适应和自校正控制。但是在实际工程应用中，伺服系统存在建模非线性、参数不确定、外界扰动和摩擦等问题尚待解决，单纯的自适应控制已经无法满足系统的跟踪性能对快速性和准确性的更高要求。结合近年来的研究成果，本研究总结了多种复合自适应控制策略，如自适应反推控制、自适应模糊控制、自适应神经网络控制、自适应滑模控制、自适应优化算法等。每一种复合自适应控制策略都有其优势，也有其不足。因此，国内外学者才会选择将更多的控制策略进一步结合，达到优缺点互补的效果。

复合自适应控制广泛应用于伺服控制的各个应用领域，如电液伺服控制系统、机械臂中的伺服控制、永磁直线同步电机，以及双惯量或者双电机伺服控制系统等。开发跟踪速度更快、精度更高的复合自适应控制系统，还有待于进一步加强算法初始参数、参数估计的优化算法、新的复合自适应控制方法以及不同算法相互结合等方面的深入研究。