基于宏应变互能量密度谱的中小跨铁路桥梁损伤识别

张 浩，钟志鑫，段君淼，王国安，郑志超

(1.石家庄铁道大学 省部共建交通工程结构力学行为与系统安全国家重点实验室，河北 石家庄 050043；2.石家庄铁道大学 大型结构健康诊断与控制研究所，河北 石家庄 050043；3.石家庄铁道大学 土木工程学院，河北 石家庄 050043；4.石家庄铁道大学 交通运输学院，河北 石家庄 050043)

近年来，我国建成各类桥梁已超百万座，成为世界第一桥梁大国，其中大部分为中小跨径桥梁。中小跨径桥梁事故占桥梁事故比例的90%以上，因此准确识别其损伤状况具有极大的应用价值。

李德葆[1]对局部损伤识别的灵敏度由低到高进行排列，得出应变类指标从总体上比位移类指标更易于对结构局部损伤进行识别。吴智深等[2]提出的“宏”应变传感技术，集结构的局部信息和整体信息于一体，具备了动静态测试的特点，具有损伤定位准确，定量精度高等明显优势。吴智深等[3]将长标距宏观应变模态向量作为损伤指标，该指标在损伤定位和定量方面均具有较高精度，在长大跨柔性桥梁中应用效果较好。但中小跨径铁路桥梁刚度大，当车桥的质量比相对较大时，车桥耦合振动效应不可忽略，结构系统将体现时变振动特性，加上列车荷载的非平稳性特征[4]，导致较难获取到桥梁准确、稳定的应变模态，因此基于宏观应变模态测试方法较难识别时变桥梁的损伤，既有宏应变传感理论直接应用于中小跨径铁路桥梁损伤识别较困难。文献[5-7]提出的基于频域宏应变工作变形的城市道路高架桥的损伤识别方法，识别损伤位置精度较高，为解决宏应变在中小跨径桥梁损伤识别应用中存在的问题提供了较好的思路，使得宏观应变损伤识别的应用范围推进到中小跨径桥梁领域，但损伤识别理论较复杂，一般的工程人员较难理解，不易掌握。

小波分析作为一种时频分析方法，对处理非平稳信号具有很大的优势，能够实现对信号数据的有效分解与降噪。刘习军等[8]将位移响应相关系数曲率和车激桥梁响应互相关函数作为损伤指标，采用小波变换的时频分析方法，对移动荷载作用下桥梁损伤进行识别。该方法可有效识别损伤位置，但对损伤程度仍难以定量。赵冶等[9]提出基于移动荷载作用下结构相应进行损伤识别的方法，通过结构损伤前后小波包系数的变化来判断结构的损伤程度，数值模拟及实验均证实该方法的有效性，表明小波分析对时变损伤识别具有独特优势。

在上述背景下，本文将基于移动质量模型的中小跨径桥梁宏观应变响应数据[10]，针对宏应变难以有效应用的问题，采用小波变换技术，对宏应变数据进行重构，频域化处理，再根据单元间互相关函数实现对宏应变频域幅值分析，构造全频域互能量密度谱单元幅值矩阵的损伤定位指标，基于该指标中的极大值互相关系数和，构造基于单元之间互能量密度谱幅值矩阵系数和的传递比作为损伤定量指标，分别从不同损伤程度、不同车桥质量比等方面进行实验验证，实验结果表明：该指标不需要获取桥梁模态信息，通过频域应变幅值，即可实现时变中小跨径桥梁的精准损伤定位和不同损伤程度的定量识别，误差保持在6%以内，具有较强的抗噪能力。

1 理论基础

1.1 中小跨径桥梁宏观应变响应

当桥梁跨度较小，车桥质量比相对较大时，移动车载作用应近似看作移动质量车桥模型，车桥系统具有时变特征，见图1。图1中，x为移动车载与左边支座的距离，v为移动车载速度，t为移动时间，M1为移动物体的质量大小，P为考虑加速度的竖向作用力。y(x,t)为梁的竖向动位移。

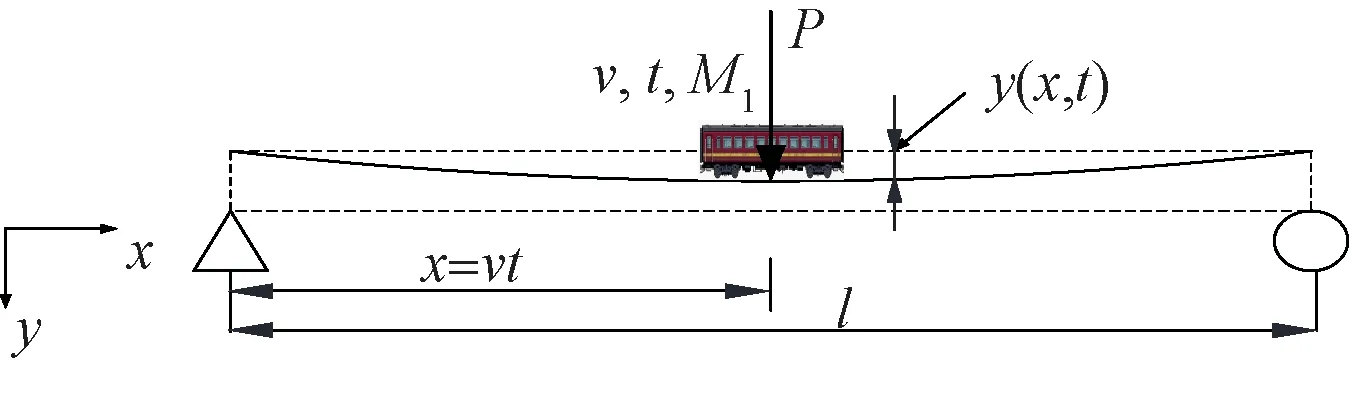
图1 中小跨径铁路桥梁车桥作用模型示意

设移动质量作用下的竖向位移为z(t)，梁所受到的作用力P(x,t)可表示为

(1)

式中：g为重力加速度。

根据不分离假定(移动质量与梁体密切)有

z(t)=y(x,t)=y(vt,t)

(2)

将式(2)代入式(1)中，可得

(3)

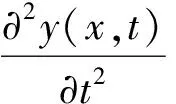
梁的动力平衡方程为

δ(x-vt)P(x,t)

(4)

式中：c为阻尼系数；δ为Dirac函数，即x=vt时δ=1，x≠vt时δ=0；EI为梁的刚度。

根据振型分解法可知，梁强迫振动的动位移y(x,t)可表示为

(5)

式中：φi(x)为第i阶振型；ηi(t)为广义坐标。

利用振型正交性和Newmark法，可得质量块移动时简支梁的竖向位移的表达式为

(6)

(7)

在单跨简支梁均匀布设标距长为Lm的应变传感器安装在梁的底部，见图2。图2中，x1和x2分别为长标距传感器两端与左边支座的距离。。传感器标距两端的转角位移分别为φ1和φ2，则在移动质量移动到任意t时刻时，该长标距传感器测量的应变为

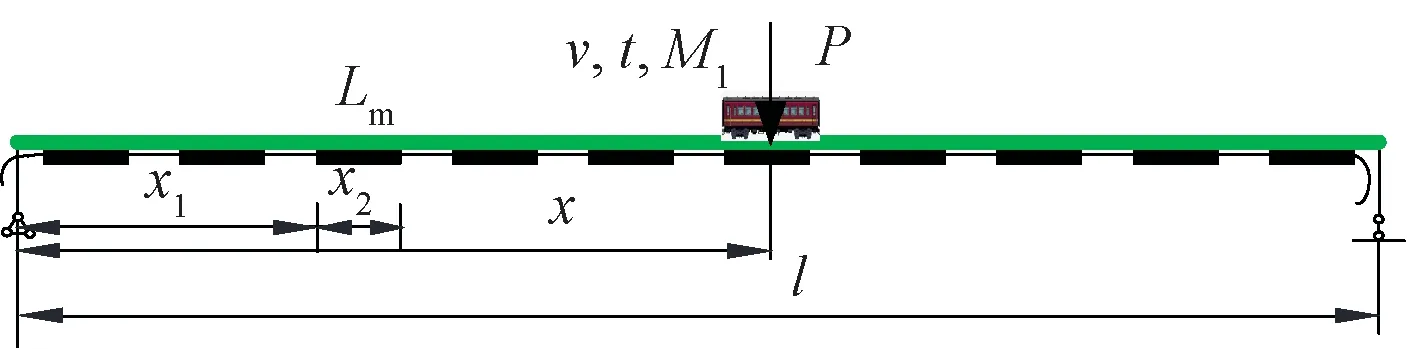
图2 长标距应变传感器测量

(8)

将式(5)和式(7)代入式(8)中，则本文所采用的时变宏应变响应的理论计算公式在时域和频域的表达式分别为

(9)

(10)

1.2 小波变换重构宏应变

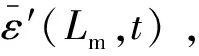
(11)

式中：ξ(t)为环境激励产生的宏应变响应信号。

因此，在对该信号进行损伤识别研究时，应考虑如何消除噪声等环境激励的影响[11-12]，从复杂的长标距动态信号中提取出有用的车辆荷载应变信号，从而实现对中小跨径铁路桥梁损伤的有效识别。

结合相关参考文献[13-16]和团队最新试验发现，对于宏观应变的降噪，Bior5.5小波基6层尺度分解所得信噪比最高。故本文采用Bior5.5小波基函数对实测宏应变数据进行6层小波分解，即

ciAi+ciDi

(12)

式中：ciAi为分解的近似部分，i=6；ciDi为分解的细节部分，环境激励等噪声部分通常包含在ciDi中。

(13)

2 损伤指标构建

2.1 损伤定位指标

jIm(w)=|X(w)|ejφ(w)

(14)

本文考虑时变中小跨径铁路桥梁因其时变性导致固有频率时刻变化，较难识别模态频率的问题，类比其宏应变传递率函数原理，选取傅里叶变换后的宏应变幅值进行互相关分析。提取该频域数据的所有单元振动幅值进行单元间互相关函数计算，选取其全频域响应数据，得到n个单元测点的全频域单元间互能量密度谱幅值向量矩阵MASV为

(15)

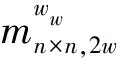
(16)

式中：T为长标距宏观应变信号的时间长度。

该矩阵既反映了时变中小跨径铁路桥梁在车桥耦合效应下，各单元之间的振动响应相关性，也间接反映了移动质量移动过程中，振动响应的衰减与叠加的双重效应的影响关系。若长标距单元间存在损伤，则与损伤单元相关的互能量密度谱幅值向量将产生突变，且随着损伤的增大，突变程度将增加。可根据该矩阵中最大互相关系数列实现损伤定位。

2.2 损伤定量指标

为最大消除单一实验误差和外激励大小对损伤定量识别结果的影响，考虑MASV中包含多组单元互相关函数向量，故采用损伤定量流程进行损伤定量识别，见图3。

图3 损伤定量流程

3 实验分析

常见中小跨径铁路桥梁跨径为24 m，按照15∶1的比例加工一个跨度为1.6 m的工字型铝合金简支梁桥进行移动车载实验，其弹性模量为69 GPa，惯性矩为1.13×10-7m4，泊松比为0.33，密度为2 700 kg/m3，质量为0.81 kg，一阶自振频率为72.15 Hz。在梁的上翼缘跨中分别粘贴10个长标距光纤光栅应变传感器，测量其压应变(取应变绝对值)，依次串联，将梁划分为10个长标距应变单元，每个长标距应变单元为16 cm，再串联1个同类型温度补偿传感器。黏结完成后对传感器波长进行标定，记录该时刻11个长标距应变传感器的波长作为初始值。车桥作用实验模型见图4(a)，移动小车质量为4.3 kg，可通过增加砝码改变其质量大小。通过减小截面尺寸和增大标距内损伤长度来实现四种损伤工况的实验分析，见图4(b)。

图4 车桥作用实验

D0—D4分别命名为无损伤、微损伤、小损伤、中等损伤、大损伤；D5—D8分别为两处位置损伤，损伤程度相同。其中截面损伤为截面刚度折减量之比，损伤长度为一个标距内的实际损伤长度，损伤程度计算方法参考文献[6]。损伤信息见表1。

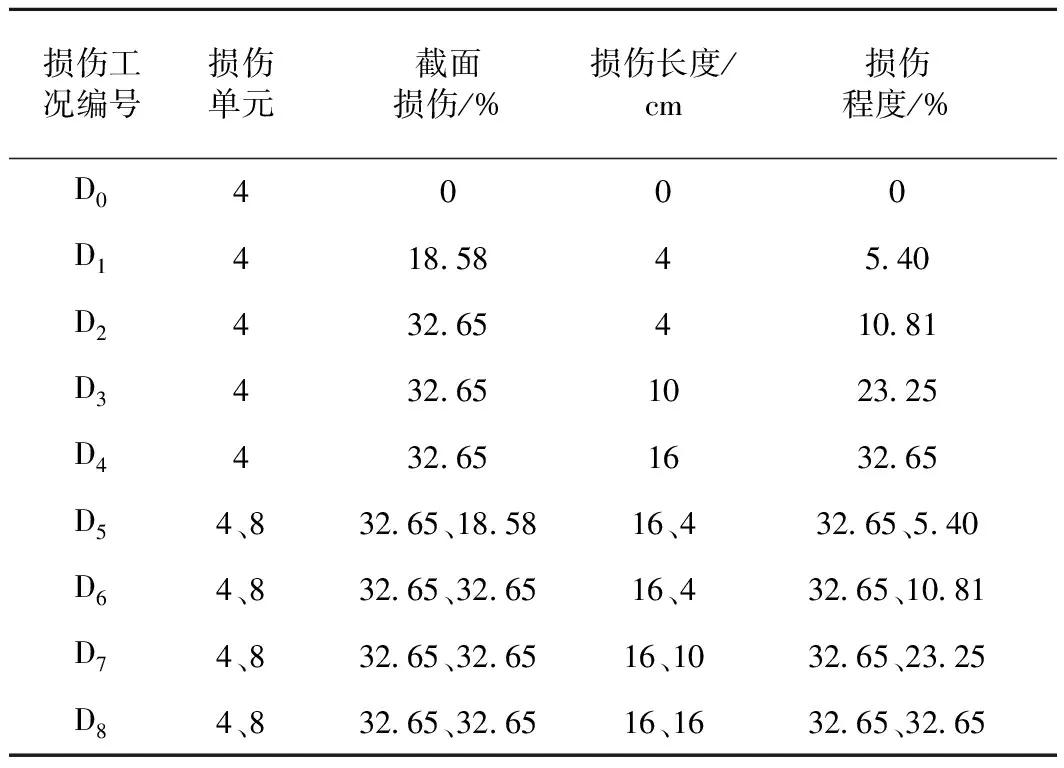
表1 损伤信息

3.1 小波变换重构宏观应变数据

对实验数据进行提取，见图5。由图5可知，由于实验存在噪声等非平稳激励的影响，导致宏观应变数据图中存在较多毛刺，如果直接对其进行分析，会产生较大实验误差。

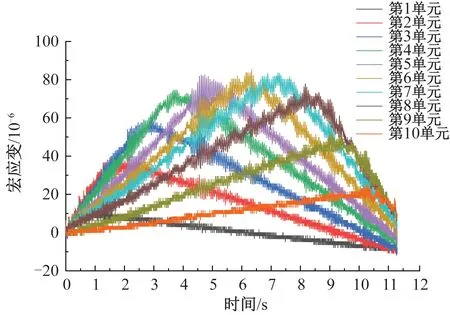
图5 移动质量作用下宏观应变

根据1.2节所提方法，对实验数据进行小波分解重构，宏观应变数据见图6，由图6可知，该数据光滑、平稳，可有效避免外界噪声等非平稳激励的影响所带来的精度误差，为后续提高损伤识别的精度提供保障。

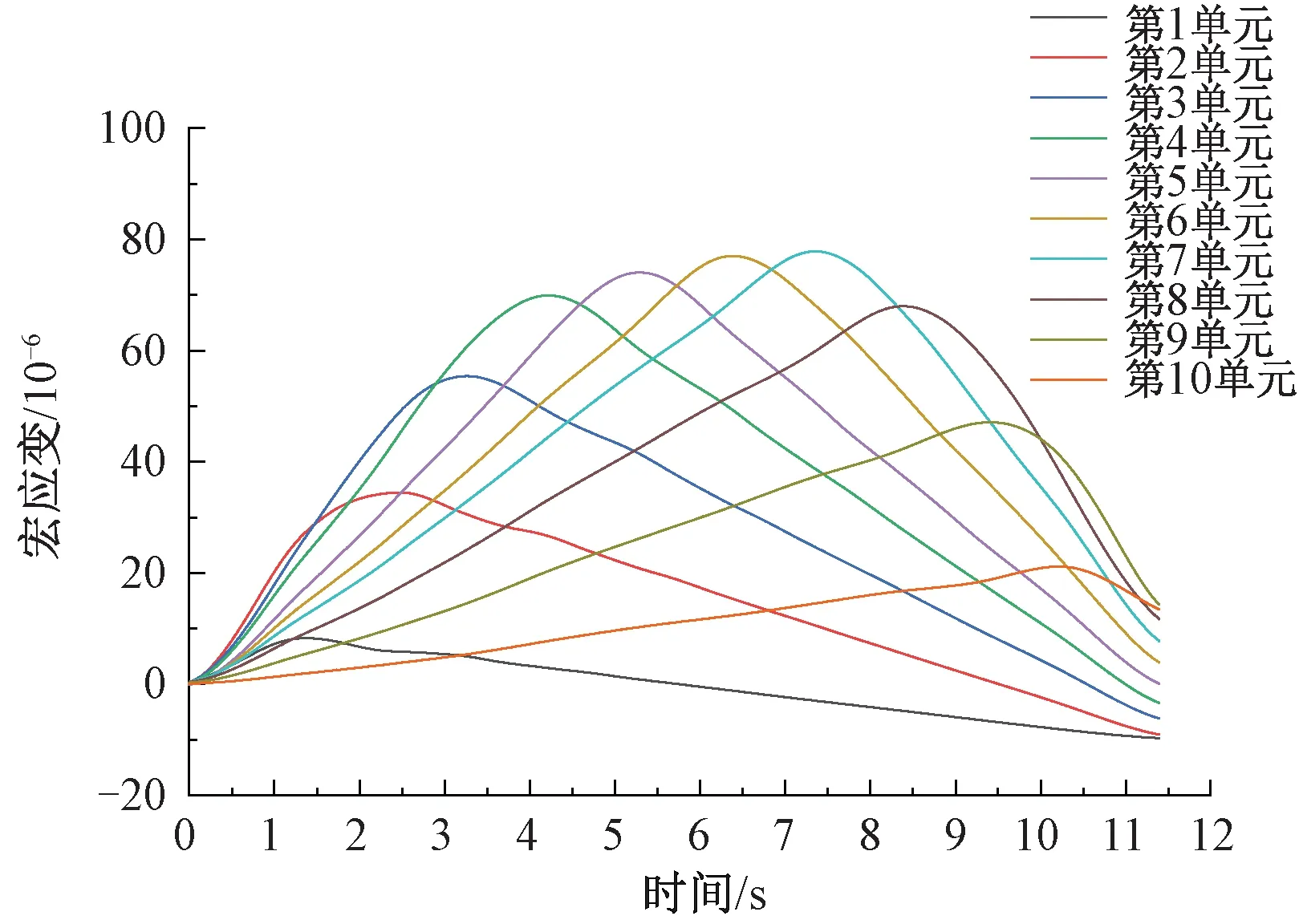
图6 小波变换重构数据

3.2 损伤定位指标影响因素分析

为验证本文所提损伤指标的准确性，并考虑到车桥作用实验激励的复杂性，故基于小波变换重构的宏观应变数据，重点对车桥质量比、损伤程度、损伤位置等可能对损伤定位指标带来的影响因素进行分析。

3.2.1 车桥质量比分析

通过增加移动小车中的砝码质量，来达到构造不同车桥质量比的移动车载实验系统。为防止桥梁被压垮，故分别设置小车质量为4.3、5.8、8.1 kg，车桥质量比分别为5∶1、7∶1、10∶1。为方便对比不同车桥比作用下的全频域单元间互能量密度增幅值向量矩阵的情况，选取两种损伤工况下最大互相关系数进行对比分析，见图7。

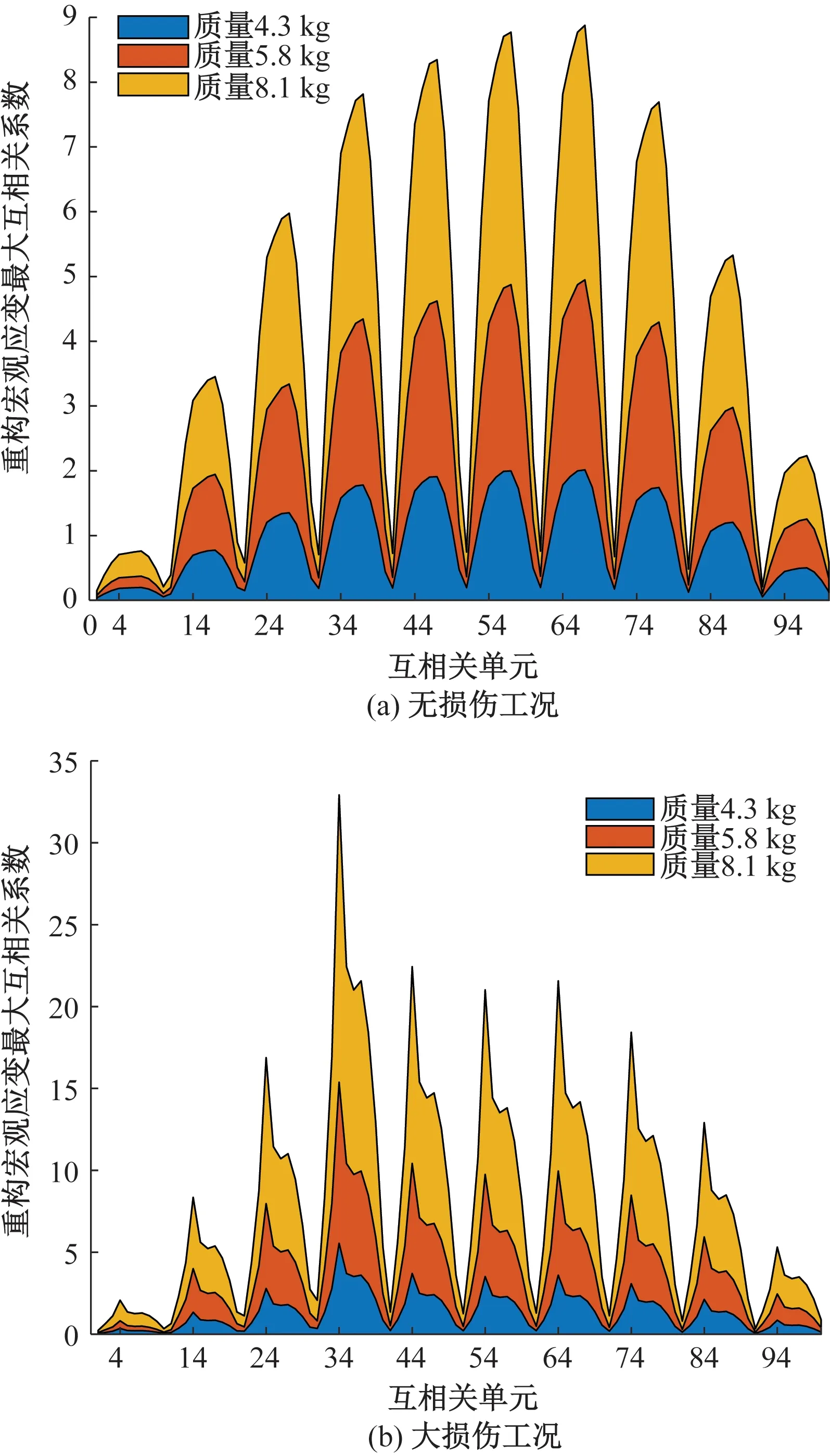
图7 无损伤-大损伤工况下不同车桥质量比的最大互相关系数

由图7(a)可知，无损伤工况下的最大互相关系数系数基本不存在明显突变，较光滑。随着车桥质量比的增加，系数逐渐增加。由图7(b)可知，在大损伤工况下，互相关单元数组{4,14,24,34，…，94}均存在明显突变，质量比越大时，该数组处突变越明显，故可将损伤位置定位于第4长标距单元。且车桥质量比值越大时，损伤定位指标的损伤定位效果越明显。

3.2.2 损伤程度影响

分别选取4.3、5.8 kg两类移动质量作用下，五种损伤工况最大互相关系数进行分析，见图8。

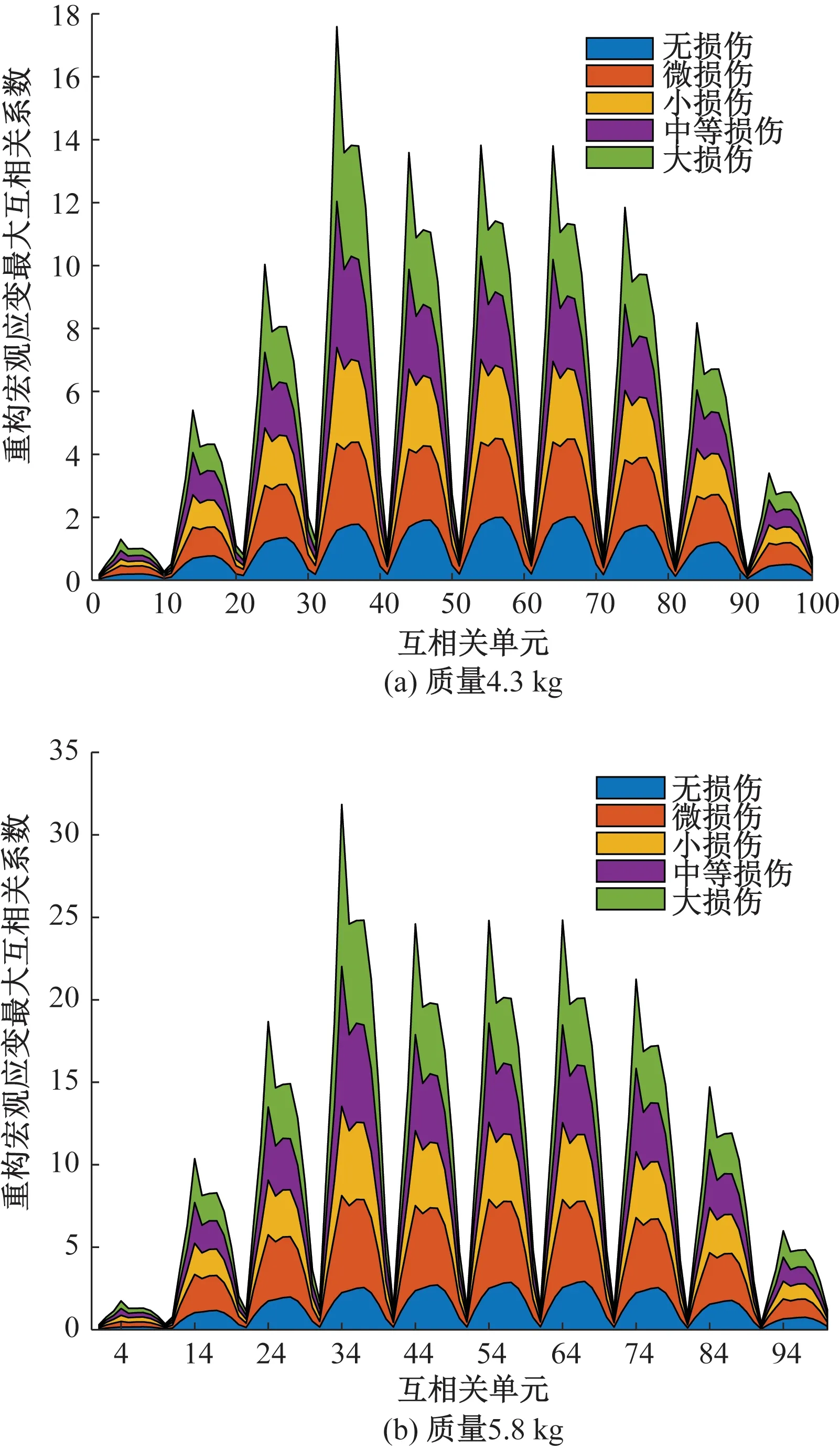
图8 质量为4.3、5.8 kg工况下不同损伤最大互相关系数

由图8可知，随着损伤程度增加，最大互相关系数系数在互相关单元数组{4,14,24,34，…，94}处逐渐增加，在微损伤工况下的突变性不够明显，但在大损伤时突变明显且达最大值。以上各类损伤工况，均可通过对比分析实现损伤的定位。故损伤程度对损伤定位指标影响不大，但损伤程度越大时损伤定位指标的定位效果越显著。

3.2.3 损伤位置的影响

在梁的第四和第八单元，分别进行损伤破坏(两单元损伤工况相同)，采用8.1 kg移动质量小车进行实验，计算九种损伤工况的最大互相关系数进行分析，见图9。

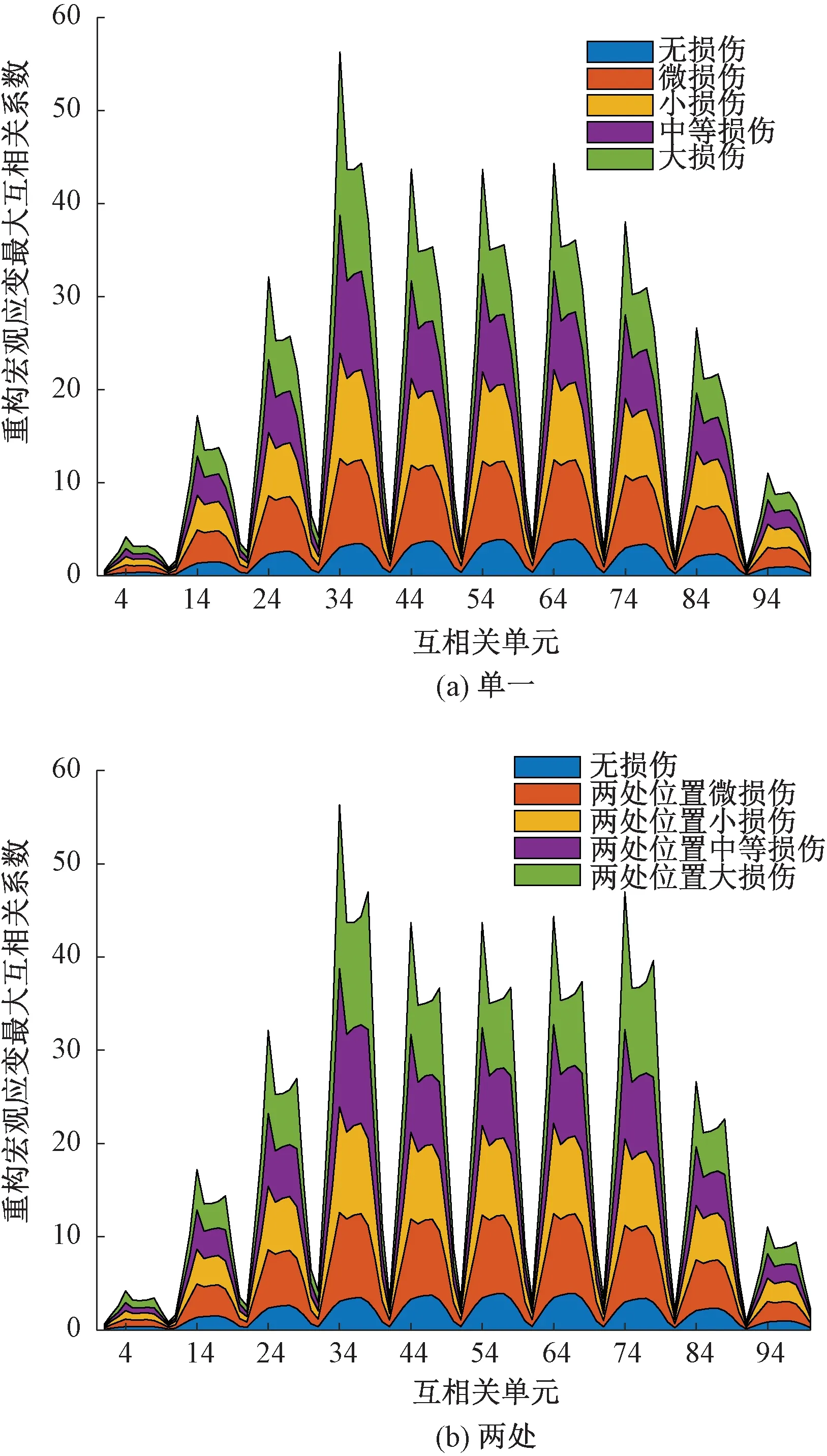
图9 质量8.1 kg单一和两处损伤位置工况下最大互相关系数

由图9可知，两处位置损伤的最大互相关系数在互相关单元数组{4,14,24,34，…，94}和{8,18,28,38，…，98}处均逐渐增加，但两处损伤在相同的前提下，前者最大互相关系数明显大于后者，故当存在多处损伤时，损伤之间会存在弱化作用，但依然能够有效识别损伤的位置，即损伤定位指标能够实现损伤的有效定位。

3.3 损伤定量指标分析

根据损伤定位结果，进一步基于所提损伤定量指标开展损伤定量识别研究。根据损伤定量步骤图，对4.3 kg移动小车作用下不同损伤程度进行定量计算，其中前两步见图10。损伤定量结果见表2。

图10 不同损伤工况下的互相关系数和及归一化相关系数和

表2 损伤定量表

由表2可知，该指标对细微损伤的识别能力较强，随着移动车辆荷载的增加，整体识别精度有所提高，相对误差均保持在6%以内，可见本文所提的基于的损伤定量指标具有较高的精度和较强的抗噪能力。

4 结论

本文基于常见中小跨径铁路桥梁的缩尺模型，通过移动车载实验提取宏观应变响应数据，结合小波变换技术，对所构造的损伤定位和定量指标进行研究，取得以下研究成果。

(1)基于移动质量作用下时变桥梁的振动方程，推导了时变桥梁振动方程宏应变响应解的表达式，并进一步建立了小波变换重构宏观应变的表达式，利用相关函数构造了全频域互能量密度谱单元幅值矩阵的表达式，并基于此建立了基于互相关系数的损伤定位与定量指标。后续将该方法进一步拓展到车桥耦合条件下的损伤识别。

(2)根据建立的损伤指标，通过实验分析常见因素影响。所提损伤指标具有较好的损伤放大功能，可针对时变桥梁的宏观应变响应进行有效的损伤分析，解决并实现对细微损伤的精确识别，误差始终保持在6%以内，具有很好的抗噪性。所提方法基于频域应变幅值，可不需考虑完整应变模态信息即可实现损伤识别，这将为基于宏观应变指标的桥梁损伤识别理论应用于中小跨径桥梁提供新思路。但所提定量指标对于多损伤位置的定量效果不够明显，故在后期将考虑继续优化损伤定量指标，从而实现多损伤位置的有效定量识别。

(3)设计的车桥模型较简单，缺乏对复杂移动车载状况(如移动速度、车轴数量)等的深入研究。故后期将考虑采用多跨连续梁、空间箱梁等复杂桥梁模型和多轴变速移动车载进行验证，进一步完善本文所提损伤识别方法。

(4)基于互相关函数进行计算，长标距单元越多，则互相关单元数量将以指数级增加，故在实桥运营中需要考虑优化单元互相关的计算方法，以降低运算工作量。