基于尾部射流的高速列车气动减阻研究

黄 莎，于 杨，李志伟，车正鑫

(1.五邑大学 轨道交通学院，广东 江门 529020；2.山东职业学院 城市轨道学院，山东 济南 250104)

高速铁路以其高效便捷、舒适安全和绿色环保等优势已成为世界各国重点发展的对象。然而随着列车运行速度、载客量、运输距离的不断提高，列车能耗大幅度增加，对节能环保提出新的挑战。为了保障高速列车可持续发展，建设资源节约型、环境友好型社会，列车的节能降耗研究迫在眉睫。

列车运行过程中的能耗主要用于克服运行阻力，在高速运行状态下列车受到的空气阻力随速度的平方急剧增加，列车空气阻力研究是高速列车减阻节能的主要考虑因素[1-3]。在铁路列车气动减阻研究过程中，随着计算机技术的发展，大批学者致力于高速列车头型设计[4-13]与局部结构优化[14-21]的研究，以达到减阻降噪的目的，取得了一系列实质性的研究成果，大大降低了列车运行阻力。然而传统的通过改变外形来提高列车气动性能的方法已趋于完善与成熟，并受制造工艺和设计要求不断提高的限制，逐步显示出其局限性，很难再有新的重大突破。因此，学者们开始致力于探索新型减阻方法。

湍流流场主动控制减阻技术是目前国际上的前沿研究领域，它在不改变物体外形的前提下，通过施加适当能量激励，改变物体周围局部乃至全局流场结构，达到优化气动性能的目的[22]。该方法在航空航天等领域已有广泛应用[23-27]，但在地面交通工具领域仅处于探索起步阶段。文献[28]采用大涡模拟的方法研究了25°Ahmed模型尾流特性，提出一种基于半正弦波信号的非定常喷流主动控制方法，与传统合成射流方法相比具有更有效的减阻效果；文献[29]采用SSTk-ω湍流模型对标准25°Ahmed模型的稳态射流减阻开展研究，在模型尾部设置射流孔，分析射流孔孔径、形状、射流速度、射流角度等参数对列车气动阻力的影响规律，得到最佳射流方案减阻13.23%的良好效果；文献[30]基于Boltzmann法，对钝体尾流结构进行射流控制，研究在钝体尾端垂直面的边界布置射流孔，结果表明当射流与来流成45°并指向地面时，具有显著的减阻效果，当射流速度为0.5倍来流速度时，减阻率高达20%。

然而，基于主动控制的尾部射流技术在高速列车气动减阻方面的研究鲜有记载，本文采用数值计算的方法对高速动车组周围流场结构和气动阻力的特性进行模拟，探索在尾部特殊流动部位设置射流狭缝，研究射流位置、射流速度等变量对高速列车流场结构和气动阻力的影响规律，得到具有最佳减阻效果的射流模式。本文研究成果为高速列车新型减阻技术的研究提供了理论基础，有助于高速铁路节能减耗可持续发展。

1 数值计算模型

1.1 几何模型

计算模型采用三车编组CRH1型高速动车组列车，见图1，三节车分别表示为头车、中间车和尾车。本文关注尾部射流对列车气动阻力的影响，因此合理忽略了车顶空调、受电弓、车底转向架、车门、车窗等复杂的外部构件。三车编组CRH1型列车总长L=80 m，宽度W=3.328 m，高度H=4.04 m。

图1 列车几何模型(单位：m)

1.2 计算区域及边界条件

采用有限体积法对CRH1型高速列车明线运行气动特性进行数值模拟，见图2。有限计算区域的建立用以保证来流和列车周围流场的充分发展，避免计算区域边界影响列车周围气流的流动特性。参考相关文献和标准[31-34]，计算区域列车头车鼻尖点距离速度入口25H，尾车鼻尖点距离压力出口(静压为0)54H，计算区域宽和高分别为30H和20H；计算区域速度入口给定与车速大小一致、方向相反的入流速度，两侧面和顶面给定对称边界条件，地面设置为滑移地面，设定滑移速度与速度入口一致。

图2 计算区域及边界条件

1.3 网格划分及无关性分析

采用切割体网格技术对计算区域网格进行划分，该方法能够在计算区域生成高质量六面体网格，复杂边界区域生成多面体网格，从而有效减小网格数量，提高计算精度。列车表面网格见图3(a)和图3(b)，为了准确模拟列车表面附面层流动，采用棱柱边界层技术对列车壁面网格进行特殊处理，棱柱层网格大于10层并按1.18的增长因子向法向方向过渡，使得黏性效应影响范围内有足够的节点，同时控制第一层网格厚度，以保证y+值满足湍流模型壁面函数的要求，附面层网格见图3(c)。由于贴近车身周围和尾流区域是列车周围流场变化最剧烈的位置，本文采用控制体网格对列车周围和尾流区域网格进行加密，见图3(d)和图3(e)。

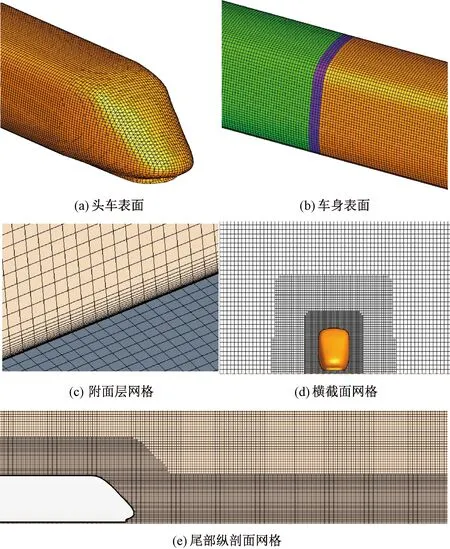
图3 计算区域网格

由于网格疏密程度对数值计算结果的影响较大，为了保证计算精度要求，同时兼顾计算资源经济合理，提高计算效率并节约成本，本文对粗糙网格、中等网格、精细网格三种不同网格密度进行了无关性验证，三种密度网格参数如表1所示，计算所得y+平均值均在30～300区间，满足湍流模型壁面函数求解条件。

表1 不同网格密度基本参数

不同网格密度下，分别对流线型尾车纵剖面压力和列车气动阻力进行比较。为了便于分析，在工程上常用无量纲系数分别表示为

压力系数

Cp=p/(0.5ρU2)

( 1 )

阻力系数

Cd=Fd/(0.5ρU2S)

( 2 )

式中：p为流场中某点的压力；Fd为列车运行中所受到的气动阻力；ρ为空气密度,ρ=1.225 kg/m3；U为列车运行速度，即远方来流风速；S为列车迎风最大横截面积，本文采用高速列车横截面面积约为11.36 m2。

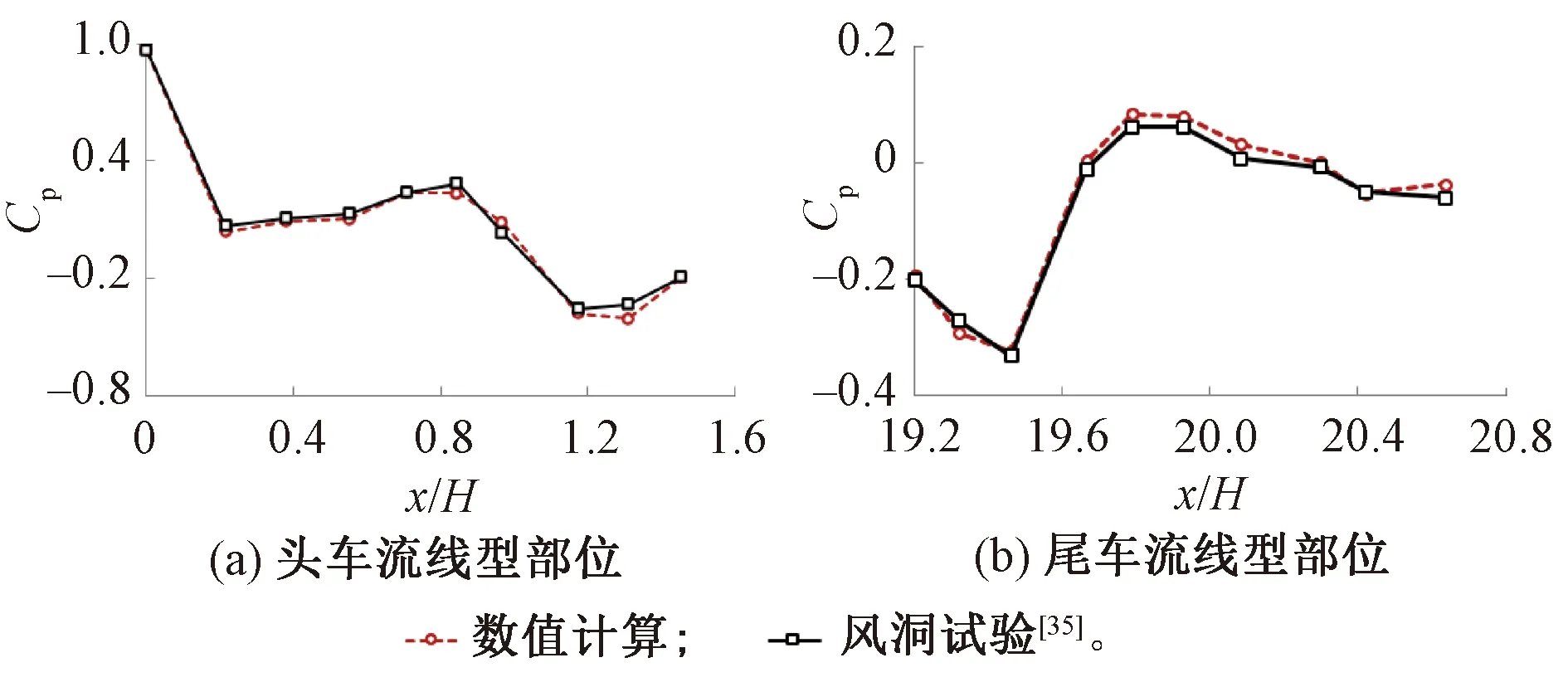
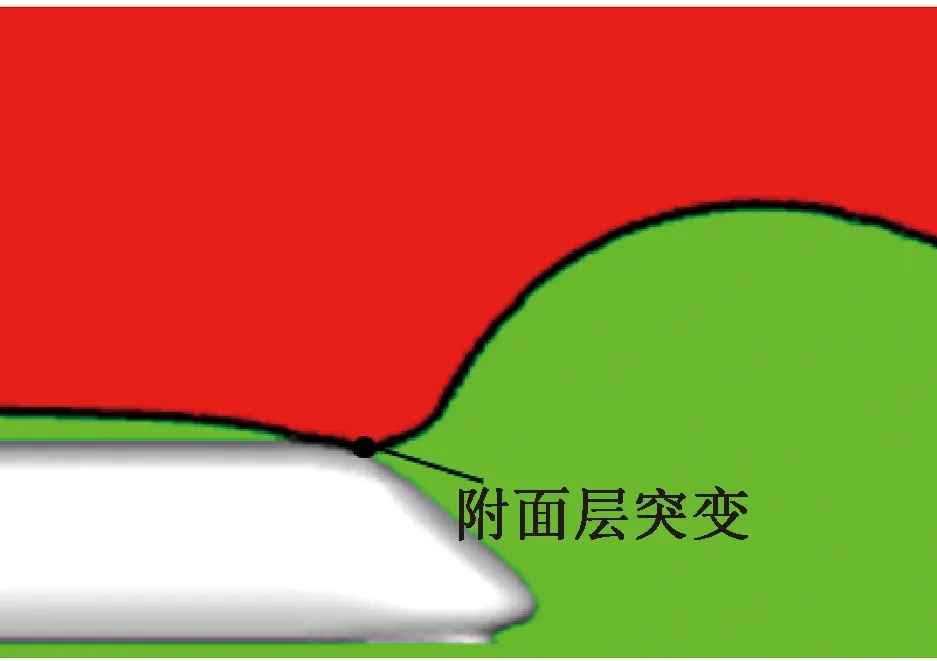
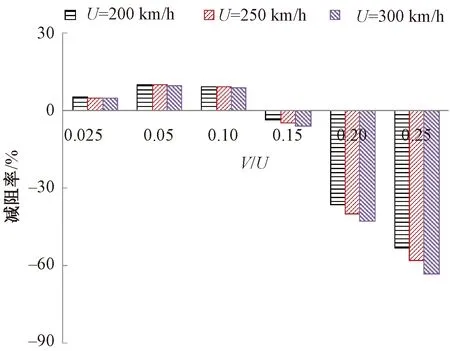
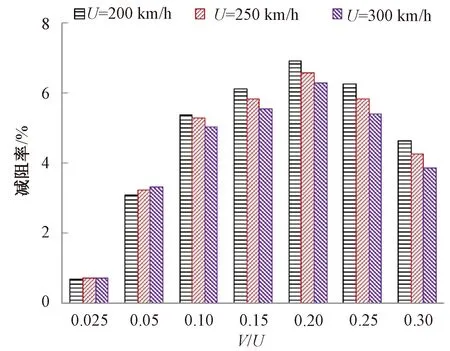
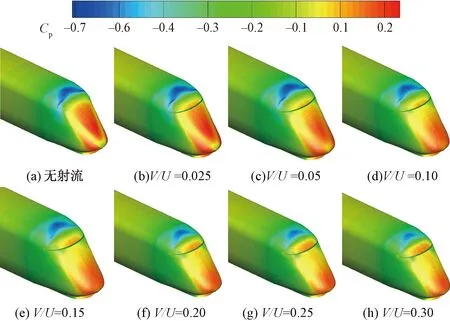
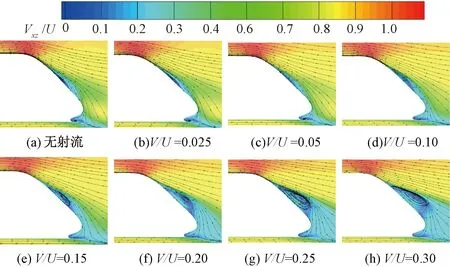
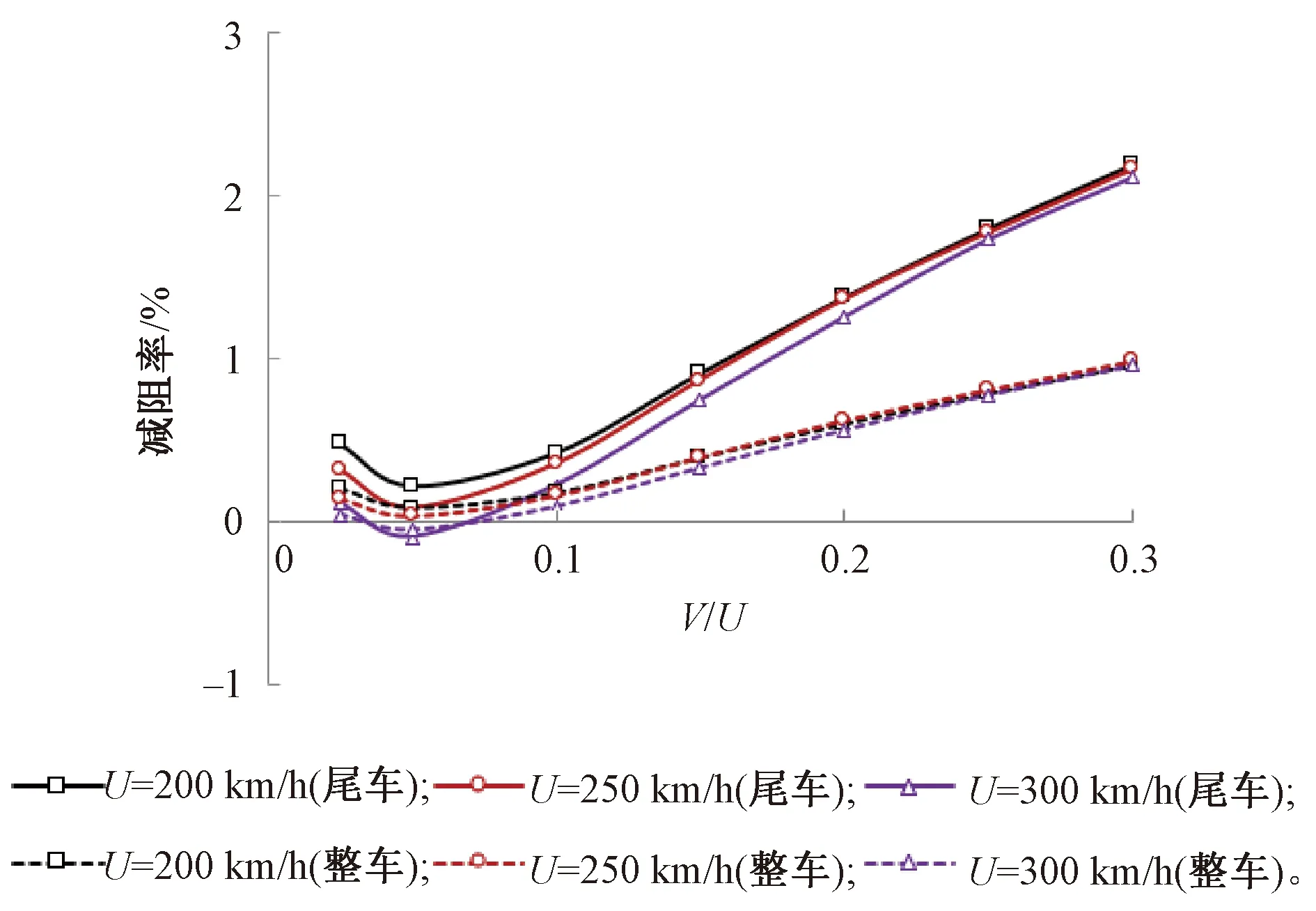
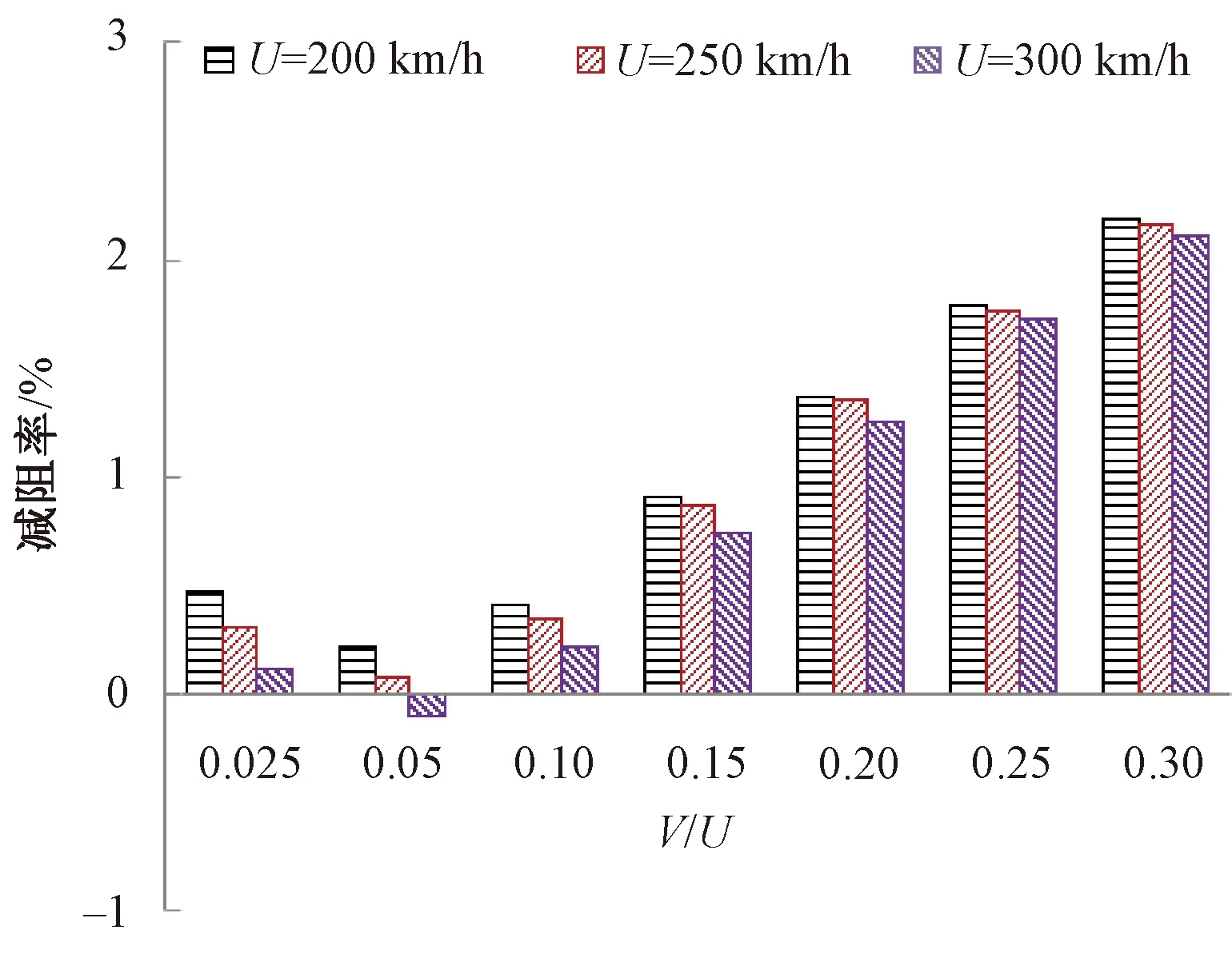
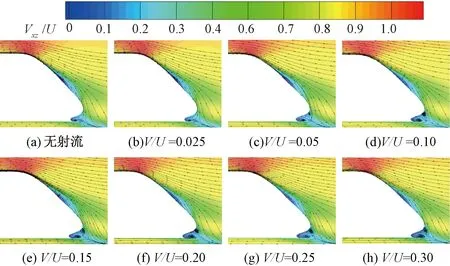
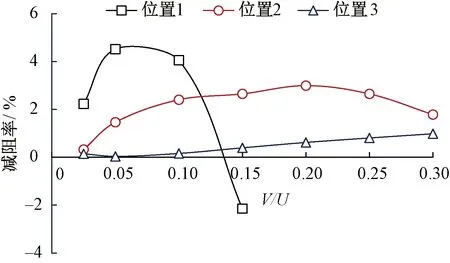
三种不同网格密度下的列车流线型头、尾车中心纵剖面表面压力系数比较见图4。图4中，z为距离轨面高度。不同网格密度列车气动阻力系数比较见图5。由图4、图5可以看出：①头车流线型部位中心纵剖面压力系数沿高度分布相差不大，差值在1%左右。②尾车流线型部位中心纵剖面压力系数沿高度0.2

图4 不同网格密度下的列车表面压力系数比较

图5 不同网格密度列车气动阻力比较

1.4 求解设置

本文采用Realizablek-ε湍流模型，它对于旋转流动、强逆压梯度的边界层流动、流动分离和二次流有很好的表现。压力速度耦合采用SIMPLEC 算法求解，控制方程压力项采用二阶迎风格式进行离散，动量、湍流动能、湍耗散率均采用QUICK格式；残差项均设置至10-6，以保证数值模拟精度。

1.5 数值方法验证

为了验证数值计算方法的正确性，采用本文所述建模方法和中等网格策略，建立CRH2型动车组明线运行气动特性仿真模型，见图6，与文献[35]在中国空气动力研究与发展中心风洞8 m×6 m高速段开展的模型试验结果进行对比。试验选用1/8缩比CRH2型高速动车组，路基和轨道模型位于距离风洞下洞壁1.06 m的支撑地板上，试验风速为60 m/s。图7给出了数值计算所得列车头、尾车中心纵剖面压力系数沿长度方向变化曲线与风洞试验结果的对比，由图7可以看出,数值计算结果和风洞试验测量结果的变化规律一致，数值计算所得头车中心纵剖面各监测点压力系数与风洞试验结果相差不大，差值均小于5%；尾车中心纵剖面各监测点压力除中部三个测点压力系数略大于风洞试验测量值，其余各测点均吻合良好。通过与风洞试验的对比，验证了本文所采用数值计算方法和网格策略正确可信。

图6 与风洞试验对比数值计算区域(单位：m)

图7 数值计算列车中心纵剖面压力系数与风洞试验结果对比

2 列车尾部射流位置确定

尾部射流主动控制方法主要是在流场中施加适当的扰动模式，通过局部能量输入，改变局部或全局的流场，从而使气动性能显著改善，主要包括：抑制/促进流动或边界层的分离、延迟/加速流动的转捩、减弱/加强湍流涡旋等。根据对CRH1型高速列车周围湍流流场的分析，可以得到以下特殊流动位置。

(1)来流流经列车鼻尖点时发生滞止，此处流速为零，表现为强正压区；经过该点后，空气向列车顶部和两侧加速流动，压力迅速下降，至流线型与等截面车身过渡位置负压最大，称为强负压区；随后气流流经等截面车身部位，压力再次回升为平稳、较小的负压，此区域称为稳流区域；当来流流至列车等截面车身和流线型尾部过渡部位时，气流加速，压强减小，产生次强负压区；同时，使附面层突变并脱离列车表面，见图8和9，此处设置适当的主动控制，将会对气动阻力产生较大的影响。

图8 列车尾部表面压力分布

图9 列车尾部附面层分布

(2)列车表面及中心纵剖面流线分布见图10。由图10可见，当气动流经列车尾部挡风玻璃上方时发生流动分离，产生涡旋结构，如何有效控制流动分离是气动减阻途径之一。

图10 列车表面及中心纵剖面流线分布

(3)基于雷诺平均的列车尾涡结构分布见图11。由图11可见，尾流区域旋涡结构在尾车鼻尖点附近脱离列车表面向远方耗散，探索在该位置设置适当的射流，抑制尾流涡旋的脱落，从而降低涡脱气动阻力。

图11 基于雷诺平均的列车尾涡结构分布

在列车尾部三个位置分别设置宽度为50 mm射流狭缝，见图12，位置1位于列车等截面车身和流线型尾部过渡位置、位置2位于尾车前挡风玻璃上方流动分离处、位置3位于鼻尖点尾涡脱落处。分别在三个位置沿狭缝法向法向以不同速度射流，探索其气动减阻效果。

图12 列车尾部射流位置

3 不同尾部射流模式对列车周围流场结构和气动阻力的影响

3.1 位置1(列车等截面车身和流线型尾部过渡位置)

在列车尾部狭小区域，低速射流对头车和中间车周围流场及气动阻力的影响不大，因此仅对列车尾车和整车气动阻力进行分析。减阻率定义为

( 3 )

列车尾部位置1(列车等截面车身和流线型尾部过渡位置)以不同速度射流时，尾车和整车气动减阻率随射流速度的变化曲线见图13。位置1仅以V/U(V为射流速度)<0.14速度射流时具有减阻效果，且V/U=0.05时，减阻率最大，列车以250 km/h速度运行时的尾车和整车减阻率分别为10.78%和4.88%，大于或小于该射流速度减阻率均呈减小趋势；当射流速度V/U>0.14后，列车气动阻力随射流速度急剧增大，表现为持续增阻。

比较不同运行速度下，位置1以不同速度射流对列车气动阻力的影响，见图13和图14。各运行速度下，列车气动减阻率随射流速度变化规律一致，均在射流速度V/U=0.05时气动减阻率最大；随着列车运行速度的增大，各射流速度下的列车气动减阻率均呈现逐渐减小的趋势。

图13 不同运行速度下，列车气动减阻率随位置1射流速度的变化曲线

图14 位置1不同射流速度下减阻率随列车运行速度变化

位置1以四种速度射流时尾车表面压力分布、中心纵剖面速度云图及流线图与无射流原型车比较见图15和图16。由图15和图16可见：射流位置后方的负压区域面积和负压值随着射流速度的增大逐渐减小，由负压带来的气动阻力逐渐减小；但随着射流速度的加大，尾部流动分离提前，分离区域面积增大，抑制了流动的再附着，造成尾部正压值逐渐减小，由于列车尾部正压区域面积较负压区大，因此当正压值减小的增阻效应逐渐大于由于负压值减小的减阻效应时，位置1射流随着速度的增大逐渐失去减阻功能。综上可知，当位置1以较小速度射流(V/U=0.05)时，尾部正压值减小量小于负压值减小量，此时，减阻效果最佳。

图15 位置1以不同速度射流时尾车表面压力变化

图16 位置1以不同速度射流时尾车中心纵剖面速度云图及流线图

3.2 位置2(尾车前挡风玻璃上方流动分离处)

在列车尾部位置2(尾车前挡风玻璃上方流动分离处)以不同速度射流时，尾车和整车气动减阻率变化见图17。当射流速度V/U=0.025时，尾车和整车减阻率接近0，分别为0.04%和0.01%，可知以V/U<0.025速度射流时，不具备减阻效果；列车减阻率随位置2射流速度的增加而逐渐增大，当射流速度达到V/U=0.2时，气动减阻率达到最大，列车以250 km/h速度运行时的尾车和整车减阻率分别为6.58%和2.99%；随后随着射流速度的继续增大，减阻率逐渐降低。由此可知，在尾部位置2以V/U=0.2速度射流时，具有最佳减阻效果。

图17 不同运行速度下，列车气动减阻率随位置2射流速度变化曲线

比较不同运行速度下，位置2以不同速度射流对列车气动阻力影响，见图17和图18。各运行速度下，列车气动减阻率随射流速度的变化规律一致；当射流速度0.0250.08后，随着列车运行的速度的提高，各射流速度下的列车气动减阻率逐渐降低。

图18 位置2不同射流速度下减阻率随列车运行速度变化

当运行速度为250 km/h，位置2以四种速度射流时尾车表面压力分布、中心纵剖面速度云图及流线图与无射流原型车比较见图19、图20。由图19和图20可见：随着射流速度的增大，尾车负压区域负压值逐渐减小；由于在分离点位置附近设置射流，射流槽上方空气受射流气流的影响发生滞止，流速降低，产生正压区，且正压值随着射流速度的增大而增加；原分离点后漩涡区强度略增大，流动再附着被抑制，因此射流槽下方的正压值减小。综合比较，在射流速度V/U<0.2时，原正压区正压值减小幅度不大，负压值减小和射流槽上方正压值增大的气动减阻效应明显；随着射流速度的增大，原尾车流动分离下方区域和再附着区域正压值减小的增阻效应逐渐明显，因此减阻率随射流速度的增加呈现减小趋势。

图19 位置2以不同速度射流时尾车表面压力变化

图20 位置2以不同速度射流时尾车中心纵剖面速度云图及流线图

3.3 位置3(鼻尖点尾涡脱落处)

在列车尾部位置3(鼻尖点尾涡脱落处)以不同速度射流时，尾车和整车气动减阻率变化见图21。当射流速度从V/U=0.025增大到V/U=0.05时，减阻率降低，但均非常小(接近0)，气动阻力变化可以忽略不计；随着射流速度的增大，减阻率逐渐增大，然而当射流速度增加到V/U=0.3时，尾车和整车的减阻率仅为2.11%和0.96%，减阻效果微弱。

比较不同运行速度下，位置3以不同速度射流对列车气动阻力的影响，见图21和图22。各运行速度下，列车气动减阻率随射流速度变化规律一致；各射流速度下，列车气动减阻率均随列车运行速度的增加而减小。

图21 不同运行速度下，列车气动减阻率随位置3射流速度变化曲线

图22 位置3不同射流速度下减阻率随列车运行速度变化

当运行速度为250 km/h，位置3以不同速度射流时列车尾车表面压力分布、中心纵剖面速度云图和流线图与原型车比较见图23和图24。

图23 位置3以不同速度射流时尾车表面压力变化

图24 位置3以不同速度射流时尾车中心纵剖面速度云图及流线图

由图23和图24可见：位置3以不同速度射流对尾车表面压力、速度云图和流线的影响不大，可能的原因包括：①由图20所示，减阻率仍有随射流速度逐渐增大的趋势，然而设置更大的射流速度将消耗更多额外的能耗，不利于整体的节能；②射流的能量远小于涡脱能量，不足以克服涡旋脱离列车表面，需探索抽、吸等更多模式的主动控制方式。

3.4 三个位置射流减阻效果比较

图25给出了列车运行速度为250 km/h时，在列车尾部三个位置以不同速度射流时整车气动阻力的变化，由于位置1以V/U>0.15速度射流时，气动阻力大幅度增大，为了清晰表达三个位置减阻效果的对比，省去位置1以V/U>0.15速度射流时的数据值。

图25 尾部三个位置以不同速度射流时整车减阻率变化

从图25可以看出，在位置3(鼻尖点尾涡脱落处)设置射流的减阻效果微弱，只有当射流速度不断增大才能缓慢减小列车气动阻力，从能耗角度考虑不宜作为射流部位；当射流速度V/U<0.12时，位置1(列车等截面车身和流线型尾部过渡位置)射流具有最佳减阻效果，整车减阻率在V/U=0.05时约为4.88%；当射流速度V/U>0.12时，位置2(尾车前挡风玻璃上方流动分离处)射流减阻效果更显著，且在射流速度V/U=0.2时减阻效果最佳，整车减阻率达到2.99%。综上可知，在尾车位置1和位置2设置主动射流控制，具有较好的减阻效果，从尽可能降低射流能耗角度考虑，位置1最佳。

4 结束语

本文采用数值模拟的方法深入分析了简化CRH1型高速列车周围湍流流场结构及气动阻力特性，通过定位尾部特殊流动部位，提出一种基于尾部射流控制的气动减阻方法，探索不同射流位置、射流速度对列车周围流场结构和气动阻力的影响规律，得到具有最佳减阻效果的射流模式：当列车运行速度为250 km/h时，在列车等截面车身和流线型尾部过渡位置设置50 mm宽射流狭缝，并以0.05倍车速沿狭缝法向方向射流能够实现尾车减阻10.78%，整车减阻4.88%的良好减阻效果，研究成果为高速列车新型减阻方式的提出提供理论基础和技术支撑。