考虑运输规模效应与网络拥堵的中欧班列运输网络优化

王臻杰，张得志，秦 进，李双艳

(1.中南大学 交通运输工程学院，湖南 长沙 410004；2.中南林业科技大学 物流与交通学院，湖南 长沙 410004)

近年来，在“一带一路”有关政策的引导下，国际外贸需求和运输需求持续增长，中欧班列开行规模也随之持续增加。根据中国国家铁路集团有限公司的相关统计，2020年中欧班列开行数量已突破12 000列，同比增长50%。但是总体而言，目前中欧班列的发展仍处于初期阶段，现行的点对点直达运输模式存在运输成本高、货运需求不足、缺乏统筹协调等问题。

根据物流产业发展规律，集散中心可以加大干线运输的开行密度，具有运量规模大、资源利用率高等优点。2020年国家发展和改革委员会下达中央预算投资2亿元，支持郑州、重庆、成都、西安、乌鲁木齐5个中欧班列枢纽节点城市开展中欧班列集结中心示范工程建设，促进中欧班列开行由“点对点”向“枢纽对枢纽”转变，加快形成“干支结合、枢纽集散”的高效集疏运体系。

但在“枢纽对枢纽”的集散转运模式下，集散中心节点可能面临因流量聚集而产生的拥堵问题，使运营效率降低，导致系统社会福利的损失。因此，综合考虑中欧班列运营中存在的运输规模效应与网络拥堵问题，合理规划集散中心选址布局以及网络流量分配，能够提升整体运营效率和社会福利，对改善现行中欧班列运营状况具有实际指导意义。

Zhao等[1]运用复杂网络理论对国内各城市节点进行重要性评价，构建混合整数规划模型对国内中欧班列集散中心进行优化选址。文思涵[2]针对中欧班列的直达班列不同线路恶性竞争等问题，从选址—运输路线安排的角度出发，建立总成本最小模型，优化集散中心等运输节点。闫伟等[3]结合直达和集结开行两种运输模式，构建中欧班列去程运输组织优化模型，并以小规模实例代入模型求出最优方案。张琦等[4]结合货物时间价值特性，优化中欧班列服务网络设计，有效降低了综合运输成本。

上述研究主要考虑静态运输成本，目前中欧班列普遍实行“量价捆绑”政策，运输生产活动中存在规模效益，即干线运输的单位运输成本会随着运量的增加而降低，因此考虑动态运输成本更符合实际[5]。另一方面，集散中转开行模式虽增加中心枢纽节点城市运输规模，但同时也可能使枢纽点出现拥堵，影响运营效率。针对中欧班列集散枢纽中的拥堵效应，蒋雪莹等[6]通过计算集拼点的拥挤与集货等待效应，构建考虑弹性需求的中欧班列集拼中心选址模型，以社会福利最大化为目标，给出在乌鲁木齐建设集散中心的建议，但没有考虑干线运输的规模效应。可见目前同时考虑中欧班列运输网络中的拥堵效应和运输规模效应的研究仍较少，难以准确刻画中欧班列集散中心选址布局以及网络中的流量分配对托运人选择行为的影响。

此外，在中欧班列运输优化中综合考虑多个决策目标的研究亦逐渐兴起。刘蒙蒙等[7]针对中欧班列集配中心选址和起始点发货周期问题，以满载率最大和总成本最小为目标构建了双层规划模型。Yin等[8]针对中欧班列的货运补贴机制问题，构建了双层规划模型，上层模型目标为最大化运输流量，下层模型目标为最小化OD对的运输成本。这些研究为从多决策主体的角度研究中欧班列运输网络优化提供了新思路。

本文遵循 “干支结合，中转集结”的思路，基于混合轴辐式网络理论，研究中欧班列集散中心选址布局与流量分配，考虑用户的弹性需求、枢纽间的运输规模效应以及网络拥堵，建立双层规划模型，在上层模型中，政府通过集散中心选址决策实现系统社会福利最大化，下层模型使用随机用户均衡来刻画托运人的路径选择行为，并使用嵌入MSA(Method of Successive Averages)的遗传算法进行求解和计算分析。

1 问题描述

中欧班列集散中心作为国家级转运枢纽，能够实现大规模干线运输，发挥规模优势，降低运输成本，从而从成本优势上吸引托运人选择集散转运；但大量流量集中在干线上可能会使集散中心或某些路段产生拥堵效应，降低转运效率，增加货物运转时间，从而使托运人的路径选择行为发生转变。因此，集散中心的选址布局以及网络中的运输规模效应与拥堵会影响托运人的服务路径选择，从而影响运输网络的整体运营效益。故需要结合实际背景，进一步分析现有5大集散中心的构建对中欧班列运输网络流量分配以及整体运营的影响规律，为中欧班列运输网络的合理布局提供决策依据。

由于直达班列、中转班列涉及运输或作业过程较多，在不失一般性的基础上，本文仅考虑货物从始发城市到终点城市之间的运输方式与路径的选择过程，对货源的聚集过程不做研究。运输网络中的货物流动简化过程见图1，本文国内货物运往欧洲终点城市的中欧班列运输方式有两种：①直达开行，即货物在中欧班列的始发城市编组装箱后直接通过西部、中部或东部路线运往边境口岸，在口岸换装清关后再运往欧洲终点城市；②集散转运，即非集散中心的始发城市货源先运往集散中心进行集结转运，再统一运输至边境口岸进行换装清关，最后运输至欧洲终点城市。由于大部分班列开行的城市之间的距离大于600 km，因此选用铁路运输将货物从始发城市运往集散中心；而集散中心自身的货物直接通过直达运输运往口岸。此过程中托运人基于自身的负效用最小来选择不同的运输方式和运输路径。经过实地调研可知，由于中转运输的成本较高，即使政府大力补贴，用户最多只会选择经过一个集散中心进行中转，因此假设通过集散模式运输的货物最多只经过一个集散中心。

图1 中欧班列混合轴辐式运输网络示意图

2 模型构建

2.1 基本假设

为便于建立模型以及反映实际情况，做基本假设如下：

①集散中心和边境口岸的周服务能力、单条运输线路的服务能力均有容量限制。

②不同边境口岸的服务能力不同，不同口岸的通关费用相同且已知。

③假设各集散中心的单位转运成本相同，服务能力相同且已知。

④运输成本分为运往集散中心的铁路运输费用和中欧班列全程平均运输费用，中欧班列全程平均运输费用根据不同的口岸通关路线进行区分。

⑤不考虑货源聚集过程。

⑥非集散中心的始发城市的货源运输可采用两种模式，一种为直接运达边境口岸的直达运输组织模式，另一种为先经过集散中心再运往边境口岸的集散运输组织模式，且货物最多只经过一次集散中心。

⑦集散中心自身的货运需求只通过直达运输方式进行，不经过其他集散中心转运。

⑧假设每趟中欧班列装载能力相同，采用20 ft集装箱装载。

2.2 参数设置

集合、参数和变量说明见表1、表2、表3。

表1 集合符号及说明

表2 参数符号及说明

表3 变量符号及说明

2.3 模型构建

2.3.1 广义费用函数构建

在选址问题中，成本一直是托运人最关注的影响因素之一[9]，时效性也是中欧班列相较于海运的一大竞争优势，因此从成本和时间的角度来构建运输服务路径的广义费用函数。成本指在托运人感知里选择路径i所产生的运输成本，时间指在托运人感知里选择路径i所花费的运输时间，通过时间价值将时间转化为时间成本。广义费用函数为

(1)

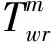
(1)运输成本

假设3个口岸的通关成本相同，为体现服务路径的差异性，不在运输成本里考虑通关成本。因此，运输路径r上的运输成本主要与该路径上的中欧班列长途运输费用、运至集散中心的短途铁路运输费用和在集散中心的转运成本(若经过集散中心)有关，运输成本为

∀r∈Rw∈W

(2)

(3)

式中：ρ为可变运输规模折扣系数，用来刻画运量规模对托运人感知效用的影响，取值参考文献[5]。

具有规模运量的中欧班列能够降低运输成本，企业对托运人的报价也会相应降低，因此本文假设对于托运人的感知来说，干线运输规模效应能够节省其运输成本。

(2)运输时间

为使模型更加符合实际情况，考虑货物在路段上以及物流节点处的拥堵，将其刻画成货物在集散中心和边境口岸的枢纽延误时间与等待服务时间。若在集散中心或边境口岸的周货物流量大于从该节点出发的弧段的服务能力，则需要进行等待，等待时间与路段服务能力和发车频率有关，频率越大等待时间越短[10]；同时若物流节点处流量超过物流节点最大服务能力，则会产生枢纽延误。因此用户在路径r上的运输时间主要由在途运输时间和在物流节点由于拥堵而产生的延误时间与等待服务时间组成，即

∀r∈Rw∈Wm∈M

(4)

m=1,2 ∀a∈A

(5)

(6)

(7)

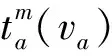
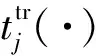
(8)

式中：Fj为集散中心j非拥堵下转运一批货物的平均时间，h。

从起点出发的货物均需经过边境口岸，且本文不考虑不同口岸基本通关时间的差异，故只考虑不同口岸由于服务容量不同所造成的枢纽延误时间。同理，货物在口岸由于拥堵所产生的平均延误时间为

(9)

2.3.2 下层规划模型

在实际物流过程中，托运人未必能够完全了解服务路径上的状况，难以完全理性地做出正确的路径选择，且确定性模型对网络流量的微小变化具有很强的敏感性，会导致结果与实际情况有着很大的出入[12]。因此，下层模型采用考虑弹性需求的随机用户均衡的网络配流模型。

随机效用理论假定决策者在面对多个备选方案时，总是选择效用最大的方案。Uwr为托运人对中欧班列运输的服务路径的随机感知效用，表示托运人选择运输路径r的成本，Uwr为

Uwr=Vwr+ξwrw∈Wr∈R

(10)

式中：Vwr为可观测的影响因素构成的确定效用；ξwr为不可观测的影响因素构成的随机项。

运输服务路径r的确定效用Vwr为其广义费用Cwr的相反数，即

Vwr=-Cwrw∈Wr∈R

(11)

因此托运人的感知效用为

Uwr=-Cwr+ξwrw∈Wr∈R

(12)

(13)

式中：θ为托运人对整个中欧班列物流网络的熟悉程度，该参数越大，托运人对整个运输网络的熟悉程度就越大，托运人间的感知差异越小。

式(13)中，运输路径r的被选择概率由运输方式间的效用绝对差所决定，当广义费用值过大的时候，将产生一些不合理的结果[14]，因此本文参考文献[13]的处理方法，采用相对效用计算运输路径的被选择概率，将概率模型改进为

(14)

式中：Cmin为中欧班列运输服务路径中的广义费用最小值。

托运人选择服务路径是基于其感知的路径上的物流负效用，因此物流用户的选择行为可用随机用户均衡模型来进行刻画，根据Logit模型，每个需求OD在可行路径r上的流量分配为

(15)

考虑中欧班列用户的需求弹性能够更好地分析运输路径的差异对货运需求的影响，因此，为了捕捉托运人对物流服务路径上的负效用的反应，引入弹性需求函数[15]，具体体现在负效用越大，其现实的物流需求越小，表达式为

(16)

式中：qw为一个连续且单调递减的函数，是关于物流OD对的预期最小服务负效用λw的函数。

根据弹性需求理论，λw为[16]

(17)

根据平衡网络流理论，上述模型中的流量应满足以下的约束条件[17]：

(18)

(19)

hwr,qw,va≥0 ∀w∈Wr∈Ra∈A

(20)

2.3.3 上层规划模型

作为上层模型决策者，政府通过决定集散中心的选址决策来实现整个中欧班列系统的总社会福利最大化。这里的总社会福利包括消费者剩余、生产者剩余以及政府支出，总社会福利Wsoc为

Wsoc=Scon+Spro-G

(21)

式中：Scon为消费者剩余；Spro为生产者剩余；G为政府支出。

(1)消费者剩余

(22)

消费者剩余可以理解为当物流用户实际支付的成本低于他们意愿支付的成本时所获得的额外的收益，其中Dw-1(w)为物流需求的反函数[12]，可表示为

(23)

根据式(23)，可得消费者剩余为

(24)

(2)生产者剩余

生产者剩余是衡量生产者福利的一个指标，可以用生产者的利润来表示，即

Spro=π-Cj-Ck-Ct-Cc-Cf

(25)

(26)

(27)

(28)

(29)

(30)

(31)

式中：Spro为生产者剩余；π为收入；Cj、Ck、Ct、Cc、Cf分别为转运成本、通关成本、运输成本、拥堵成本和建设成本；P1为中欧班列的平均定价收费；s为政府对中欧班列企业进行的补贴率。

式(26)表示中欧班列企业的运输收入；式(27)表示货物在集散中心的总转运成本；式(28)表示货物在边境口岸的总通关成本；式(29)表示货物在运输网络中所产生的总在途运输成本，货物经过干线运输具有运输规模效益[7]。式(30)表示拥堵成本函数，集散中心的货运量超过集拼中心的服务能力之后，货物会因拥堵而停留在集散中心，极大降低了运营效率，因此本文引入幂指函数，刻画因集散中心流量超过集散中心服务能力而产生的拥堵成本[18]。式(31)为集散中心的总建设成本。

(3)政府支出

政府支出主要指政府对中欧班列公司进行补贴所支出的费用，政府支出G为

(32)

因此，上层模型的目标函数是物流系统的社会福利最大化，可以表述为

maxWsoc=Scon+Spro-G=

(33)

s.t. 式(3)

Yj={0 ， 1} ∀j∈J

(34)

(35)

(36)

hwr,qw,va≥0 ∀w∈Wr∈Ra∈A

(37)

3 求解算法

由于所建立的中欧班列集散中心选址双层规划模型为非线性规划问题，且中欧班列运输网络中的始发城市与集散中心数量较多，模型的规模较为庞大，采用精确算法求解困难，而遗传算法在求解运输选址问题上的优越性明显，具有良好的全局优化搜索功能，能够保证解的多样性，因此本文采用遗传算法对上层规划模型进行求解，并嵌入MSA法对下层模型进行求解。算法流程见图2。

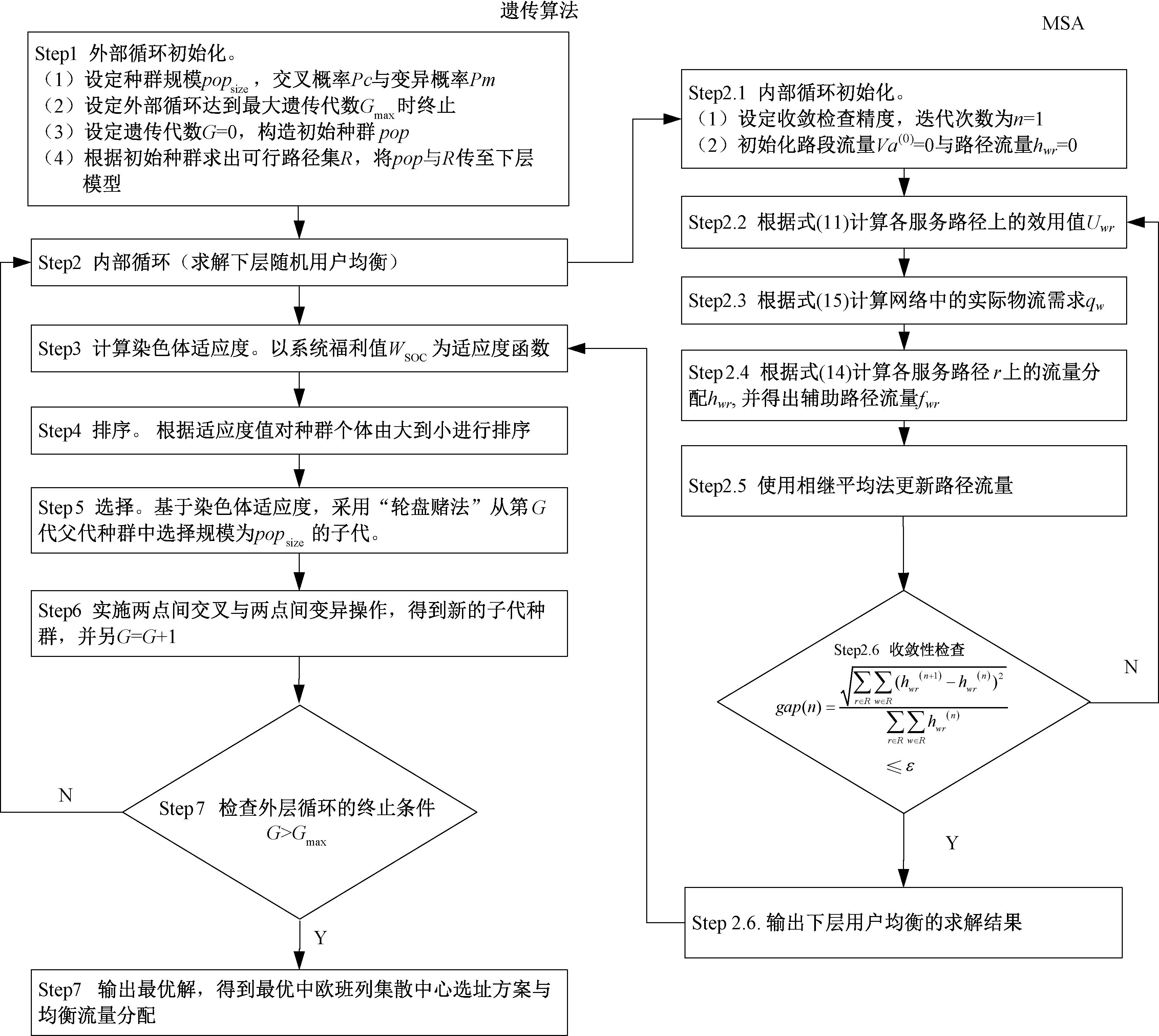
图2 算法流程图

4 算例分析

4.1 背景情况

本文在政府部门已投资构建5大集散中心的背景下，针对“起点城市—集散中心—边境口岸—终点城市”的混合轴辐式运输网络问题，从中欧班列系统社会总福利最大的角度出发，构建考虑运量规模、网络拥挤效应以及托运人弹性需求中欧班列集散中心选址网络。在结合文献[19]提出的主要中欧班列开行城市以及目前发展较好的中欧班列的基础上，考虑数据的可得性，从国内已开行班列的城市中选取西安、成都、重庆等20个国内的城市作为始发城市，同时他们也是候选的集散中心，其中西安、成都、重庆、乌鲁木齐和郑州已被选为集散中心，具体见表4。由于中欧班列国际运输路线大部分需要在满洲里、二连浩特和阿拉山口这3个边境城市进行转清关出境，因此选择上述3个边境口岸城市作为口岸节点。中欧班列运输网络中的多条线路均通过莫斯科这一枢纽城市，同时莫斯科也是欧洲最重要物流中转中心之一，本文选择莫斯科作为国外目的地城市。

表4 供应点城市表

4.2 算例数据

为方便仿真和分析结果，根据对长沙货运统计中心以及长沙北站的实地调研，在参考现实数据和现有相关文献的基础上确定算例参数见表5。

表5 参数列表

城市节点之间的铁路运输距离通过参考铁路内部数据和原中国铁路总公司95306网站，鉴于篇幅的原因不在此列出。另外，考虑建设成本是大规模的支出，而模型涉及的其他成本是以周为单位的，因此直接使用30 000万元作为集散中心的建设成本会对选址的决策造成影响。假设一个集散中心的使用周期为10年[20]，大约300个运转周期，集散中心的建设成本分摊到每个运转周期之后设定约为100万元。

本文根据班列开行实际情况，整理了2020年国内20个始发城市到莫斯科的平均周货运输需求数据，并整理见表6。

表6 2020年莫斯科的周货运需求量

4.3 计算分析

将算例数据输入模型，在处理器为Intel i5-6300HQ CPU@ 2.30 GHz、4 GB内存、64位Windows10系统的笔记本上，利用Visual Studio2019进行求解。算法参数设置方面，由于算法的收敛速度较快，解空间离散且规模较小，故在参考相关文献以及进行参数实验的基础上，将集散中心的选址实例计算的种群规模设置为70，迭代次数为200代，交叉概率为0.5，变异概率为0.01，算法运行10次，选取最好解，最好解的选址结果趋于收敛。(由于集装箱个数为整数，故流量分配结果做四舍五入处理；城市与路段为便于表达用表2中的序号代替，满洲里、二连浩特与阿拉山口分别用21、22、23代替。)

最优选址方案见表7，5大集散中心以及3个口岸节点的在算例水平下的均衡流量分布见图3。从枢纽的容量利用率来看，在算例水平下网络中未出现拥堵现象，故这里主要分析网络中的运量规模效益，拥堵效应将在后面的灵敏度分析部分进行探究。枢纽节点的流量由该节点自身的流量需求与外部流入的流量需求组成，西安和成都的节点流量分别排行前二，原因在于这两个城市自身的货运需求较为巨大，加之吸引了部分的外部流量；郑州虽然自身的货运需求较少，但其吸引了最多的外部流量，原因在于郑州位于我国地理的中心区域，具有较为良好的区位优势和足够的辐射范围，吸引了大部分的外部货源；乌鲁木齐自身的货运需求最少，但由于其离阿拉山口口岸较近，是大部分经阿拉山口出境的中欧班列线路的必经之地，亦吸引了较多的外部流量。

图3 集散中心及边境口岸流量分布

表7 中欧班列国内集散中心选址优化方案

达到规模经济为的路段见表8,由表8可知，在算例参数水平下，主要是经过集散中心的干线运输路段先达到规模经济效应，支线路段上的流量较小，大部分没有达到规模效应。可见在目前中欧班列进行量价捆绑的情况下，当网络中的拥堵较少时，干线大规模运输所带来的运输成本的优势是吸引托运人选择集散转运的方式的原因。

表8 达到规模经济的路段

分析上述结果可知，在网络中拥堵现象较少时，集散中心的选址可以结合两方面的因素来考虑：城市自身的货运需求和城市所在的地理位置。从城市自身的货运需求来说，当集散中心自身具有较大的货运需求时，有利于发挥干线运输的运量规模效应优势，从而降低运输成本，吸引其他城市的托运人进行集散转运。从城市的地理位置角度出发，当集散中心具有良好的区位条件和足够的辐射范围时，能够避免和减少因迂回、对流运输等不合理运输问题所造成的运输费用增加与运输资源的浪费，故亦能吸引其他城市的货运集散需求，同时也有利于整体社会福利的提高。

4.4 货运需求变化分析

受我国政策和世界经济的影响，中欧班列发展势头强劲，未来的货运量将会稳步上升，在运量规模增长的情况下，目前的5大集散中心构建的布局可能会需要进一步做出改变。因此，本文进一步分析中欧班列货运量增长以及当网络中出现拥堵时，集散中心的布局变化以及托运人运输路径选择的变化，结果见表9。

表9 货运需求增长下社会福利及成本变化

由表9可知，优化后系统最大社会福利随着货运需求的增加而增加，可见有序增大中欧班列货运量规模是提高社会福利的关键策略。随着货运需求从1.0倍增长至3.0倍，运输成本在总成本的占比逐渐减少，拥堵成本在总成本的占比逐渐增大，可见随着运量规模的增加，干线运输上的运量规模优势越来越大，有效降低了总体的运输成本；但运量规模增加的同时也加重了集散中心处的流量拥堵，使得拥堵成本增加。

由优化前后的结果对比可知，优化前，随着运量规模的增加，现有的5大集散中心拥堵现象加剧，难以满足货运集散需求。当货运需求增长为原来的1.5倍时，原有的5个集散中心出现了拥堵现象，产生拥堵成本，拥堵成本占总成本的0.393%，但此时的拥堵成本相比于新建集散中心的成本，以及由于流量聚集所带来的干线路段上的运输规模效应优势来说，尚在可接受范围，故暂不需要新建集散中心。但当货运需求增长为原来的2倍时，原有的集散中心拥堵加剧，拥堵成本急剧上升，占10.07%，之后拥堵成本占比随着货运需求的增长而大幅增加，使得网络中的社会福利减小以及中欧班列的运营效率下降，故需要新建集散中心分担货流量。而优化后的选址方案新增了5个集散中心，原有的5个集散中心的部分货流量转移到了新建的集散中心，在达到干线运量规模经济的同时减缓了枢纽节点的拥堵，提高了最大社会福利。此外，优化后的集散中心数量一直维持在10个，且新增的集散中心大致相同，太原、徐州、石家庄和济南一直被选为新的集散中心，太原和徐州位于我国中心位置，且距离3个边境口岸的距离较近，能够很好地覆盖我国东北地区的货源；而济南和徐州位于我国的东部沿海区域，在此构建集散中心能够很好地形成中欧班列与东部海港的海铁联运运输链，扩大中欧班列的货源市场，整体提高运力，可见优化后的集散中心布局具有有效性和合理性。

综上所述，在算例水平下，当货运需求增加时，网络中的社会福利会随之增加，但同时网络中的拥堵也会增加，导致班列运营效率降低，拥堵成本增加。当货运需求增长为原来的1.0～1.5倍时，网络中由于流量聚集所带来的运输规模效应优势相较于拥堵成本来说要大，故暂不需要新建集散中心。当货运需求增长为原来的2.0～3.0倍之后，拥堵成本急剧上升，需要新建5个集散中心来满足货物的集散转运需求，以平衡网络中的拥堵与运输规模效应，使网络中的社会福利得到提高。新建的集散中心选址可优先考虑地理位置较优的太原、徐州、石家庄和济南。

5 结束语

针对中欧班列混合轴辐式运输网络优化设计问题，构建了上层目标为社会福利最大化和下层为随机用户均衡的双层规划模型，并设计了嵌套MSA法的遗传算法进行求解。以现有的5大中欧班列集散中心为现实背景，在考虑用户弹性需求、干线运输规模效应和网络拥堵的基础上，结合实际数据对中欧班列集散中心布局和流量分配方案进行优化分析，并挖掘货运需求对优化方案的影响。结果表明：首先，在进行集散中心城市的选址时，选择自身货运需求较大或者区位条件较好的来新建集散中心能够提高网络系统中的社会福利。其次，有序增大中欧班列货运规模能够产生运输规模效应，提高系统中的社会福利；但同时也会加剧网络中的拥堵，使网络的运营效率和社会福利降低。可通过增设新的集散中心来满足货物的集散需求和提高系统社会福利，新集散中心的选址可优先考虑太原、徐州、石家庄和济南。未来将针对多起点、多终点、多种不同类型货物的大规模快运班列运输网络优化问题进行进一步的拓展研究。