轻量化铝合金骨架车车架有限元分析

高 庆， 徐建建， 宿 峰

(1.山东信息职业技术学院 智能制造系，潍坊 261061；2.山东轻工职业学院 纺织服装系，淄博 255300)

随着物流及快递业的高速发展，以灵活、高效运输物资著称的半挂车在物资交换的运输方式中起着越来越重要的作用，集装箱骨架车就是一种适应“大”物流和“高速”快递的新型半挂车.现有的集装箱骨架车大多由碳钢材质的钢板和型材制作，碳钢产品重量大，且在潮湿环境中极容易生锈，大面积的生锈可能影响材料性能，因此，碳钢产品在制作完成后必须进行表面处理(喷涂、喷漆等).因此，寻找使用力学性能更优的新材料是半挂车轻量化的重要途径之一.铝合金材料因其刚度大、强度高、密度小等良好性能成为汽车轻量化选择的理想材料[1].在满足强度和刚度的情况下，铝制骨架车身比钢制骨架车身重量轻1/3，能使成本明显降低，进而使运输效率大幅度提高.

目前，国内外许多学者在半挂车车架轻量化方面作了大量的工作[2-8]，取得了很多有价值的研究成果，如总结了车架底盘的总体建模规律，构造了车架的数学模型等.但以往研究多集中于钢制车架，对铝合金车架等新材料车架的研究少之又少.因此，对铝合金骨架车车架建立有限元模型，在此基础上进行静态和模态分析，为分析新材料车架的刚度、强度及振动情况提供理论基础，是急需解决的问题.

文中以某企业设计生产的轻量化铝合金骨架车车架为研究对象，由三维建模软件SolidWorks建立了某公司研发的轻量化铝合金骨架车车架的三维模型，再通过SolidWorks插件中的simulation分析模块对车架三维模型在4种特殊工况(弯曲(满载)、扭转(满载)、紧急制动及转弯)下进行了静力学有限元分析，获得了该车架模型的位移和应力分布情况.对车架三维模型进行有限元模态分析，预测外部激励和该车架设计结构之间的相互影响，获得了该车架1-16阶的模态频率和振型特征.

1 车架有限元模型建立

1.1 结构分析

铝合金骨架车车架结构为焊接式，如图1所示，主要包括：用于承载车辆自重和物资重量的左右工字型纵梁，纵梁由两组翼板型材和中间腹板焊接而成；两纵梁中间焊接有多组前后横梁，共同组成车架结构；在车架前侧鹅颈处有起加强作用的加强板；在车架前侧有安装牵引销的牵引销板.整个车架采用6061T6铝-镁-硅系可热处理强化铝合金，其具有再加工性好且加工后不易变形、电镀性与耐腐蚀性良好、焊接性能强、抗氧化性好、易抛光和上色膜等特点.6061-T6铝合金密度为2.7 g/cm3，强度(抗拉)为310 MPa，屈服强度为276 MPa.

图1 铝合金骨架车车架三维模型图

1.2 结构简化

为了能正确反映出铝合金车架的相关力学性能，建立三维模型时省略去了车架上很多附件结构，例如工具箱、软管箱、灯架支撑杆、侧防护架等，在进行静力学分析和模态分析时它们对应力、应变的分布及模态频率和振型影响不大.此外，对于车架的结构圆角、倒角等工艺设计也不予考虑.

1.3 网格划分

在保证真实反映力学性能的前提下，可以选取较少的节点和单元[9]，对车架的所有模型结构进行网格简化处理.在进行网格划分时，网格划分的细密度会影响到计算的精度和速度，因此，对车架结构的不同区域部位采取不同网格细密度的划分：薄壁和厚壁连接处、应力集中易产生区等相对重要区域和部位，要划分多而细密的网格；对于起辅助和加强作用的加强板、肋板等部位，可以划分稀疏的网格.最终划分好网格的车架有限元模型，如图2所示，共有182 021个实体单元solid，322 772个节点.

图2 车架有限元模型

2 静态分析

文中选取了具有代表意义的4种基本工况进行分析，它们分别是车辆满载时车架的弯曲变形时的弯曲工况、车架静态扭转时的扭转工况、车辆制动时的制动工况、车辆转弯时的转弯工况[10-11].这些工况都是骨架车在行驶过程中经常遇到的工作状况.

《GB1589-2016》规定三轴半挂车最大允许总质量限值为40 000 kg，因此，纵梁和横梁上平面承受的最大载荷为40 000 kg，方向垂直于平面向下.车架的重力视为惯性载荷，取重力加速度9 800 mm/s2，方向为竖直向下.

2.1 弯曲工况

分析弯曲工况主要是分析满载且匀速行驶或静止状态时车架结构的应变、应力分布情况，从而评价出车架等相关结构的静态刚度和静态强度.在车架的前后左右共设计了六套吊耳和支座，可连接空气悬挂或板簧悬挂.

车架结构的弯曲工况分析主要是分析在满载匀速行驶时的车架应力和变形，对车架结构的静强度和刚度进行评价.弯曲工况边界条件为：在X、Y、Z三个方向上，对车架牵引销滑板处施加固定约束，在垂直于Y方向上对位于车架最后侧吊耳和固定支架施加垂直的位移约束.施加约束和力的情况如图3、4所示.

图4 弯曲工况载荷示意图

由图5、6可以得出：弯曲工况下，在牵引板与车架纵梁的连接部分获得最大为113.6 MPa的等效应力值，另外，纵梁在最前侧车桥处也存在应力集中现象，车架剩余部分的应力值基本都在70 MPa以下.由于铝合金车架材料的屈服极限为275 MPa，从图中可以看出：车架结构的最大应力值小于其屈服极限.因此，铝合金车架结构的强度满足材料性能要求.可以看出，由于车架中前面没有支撑，也在一定程度上造成了车架后面的刚度较低，由半挂车车架的刚度检验标准可知，各点处的最大位移不得大于20 mm，从图中可知，骨架车车架由于变形而产生的最大位移量为14.32 mm，符合要求.

图5 应力云图(弯曲工况)

图6 位移云图(弯曲工况)

2.2 扭转工况

半挂车低速行驶在坑坑洼洼的路面上时，非对称支撑或非对称载荷会产生静态下的扭转矩，而迫使车架发生静态下的扭转，这是在半挂车工作过程中的一种常见危险工况.扭转工况边界条件为：在X、Y、Z三个方向上对车架牵引销滑板施加的固定约束，视为最后面的车桥的左轮处于悬空状态，所以，对于右侧最后面的悬挂支撑不加任何约束，在垂直于Y方向上对其余固定支架和吊耳处施加位移约束.施加约束和力的情况如图7、8所示.

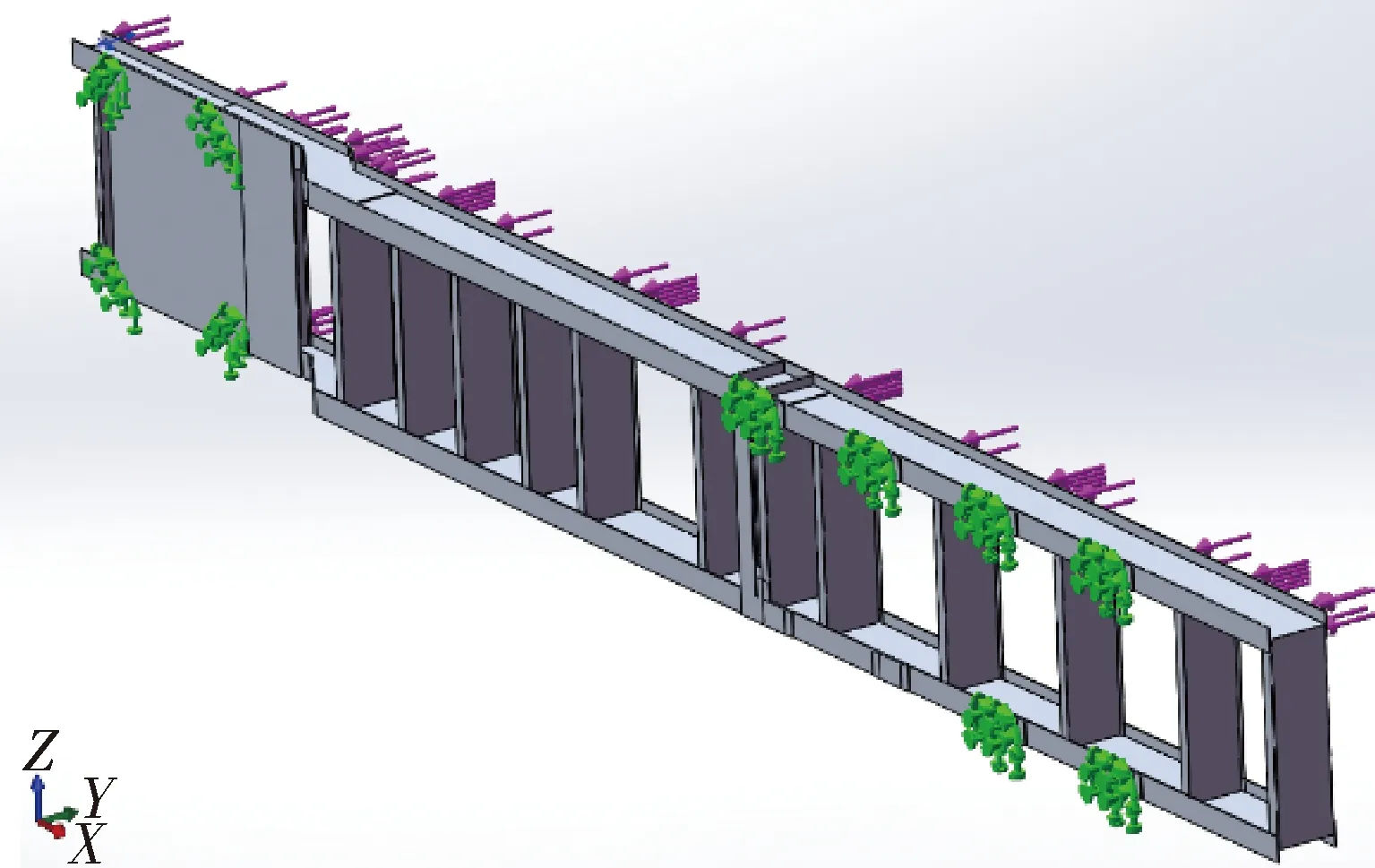
图7 扭转工况约束示意图

图8 扭转工况载荷示意图

由图9、10可以看出：扭转工况与弯曲工况类似的是在牵引板与车架纵梁的连接部分仍然会产生较大的应力集中现象，两者的不同部分主要表现在左侧纵梁的后轮悬架安装处也存在应力集中现象，而其它悬架安装处应力分布比较均匀，无应力集中现象.车架剩余部分的应力值都较小.此工况下，车架结构的最大等效应力(VonMises)为109.2 MPa，其值小于车架设计结构和材料性能对强度要求值(275 MPa)，因此，可以认为此车架结构在此工况下强度是符合要求的.在铝合金车架纵梁的中前部分和左纵梁后部都产生了较大变形，其因车架变形产生的最大位移量为15.12 mm，小于规定值(20 mm)，符合要求.

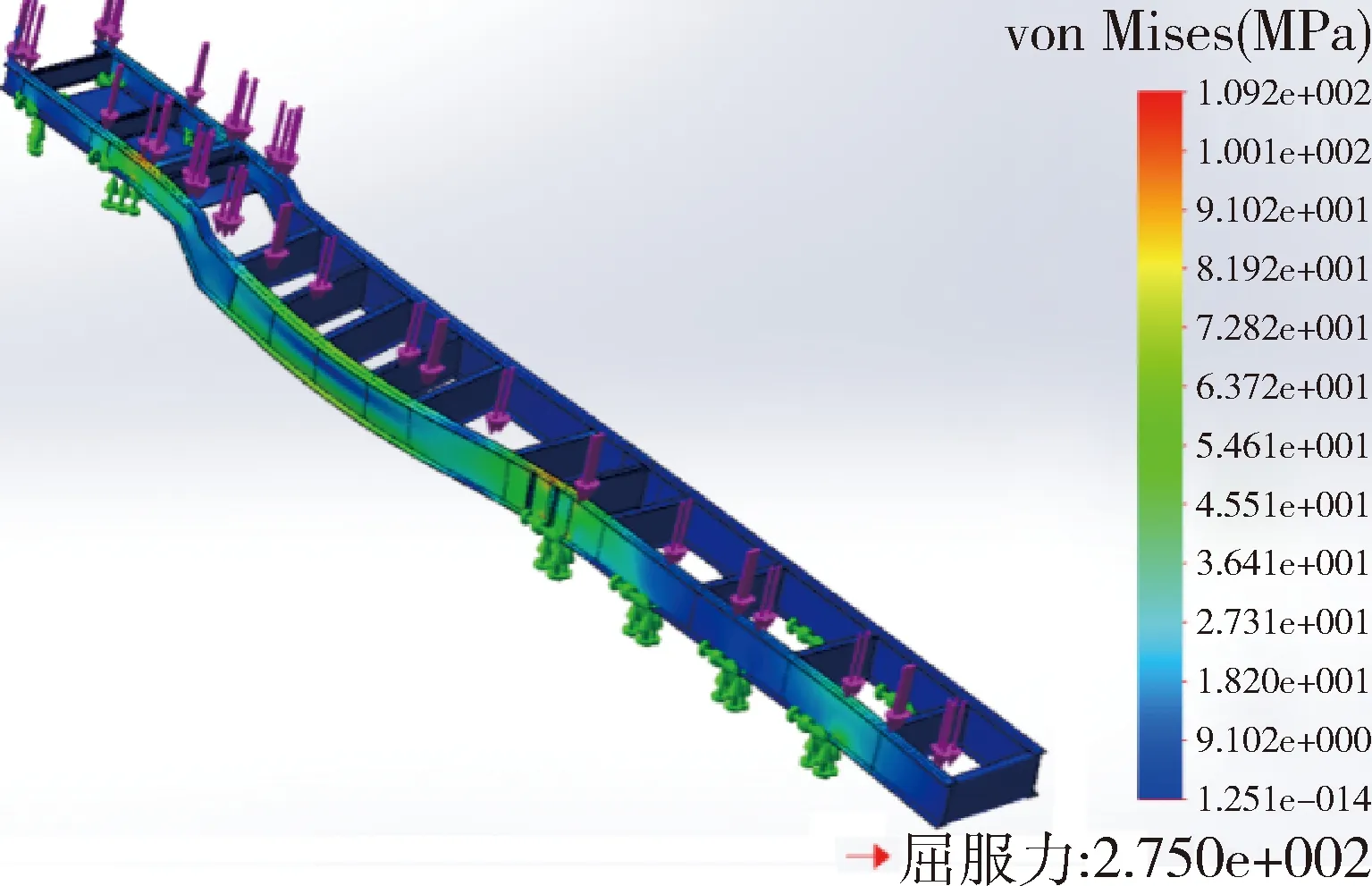
图9 应力云图(扭转工况)

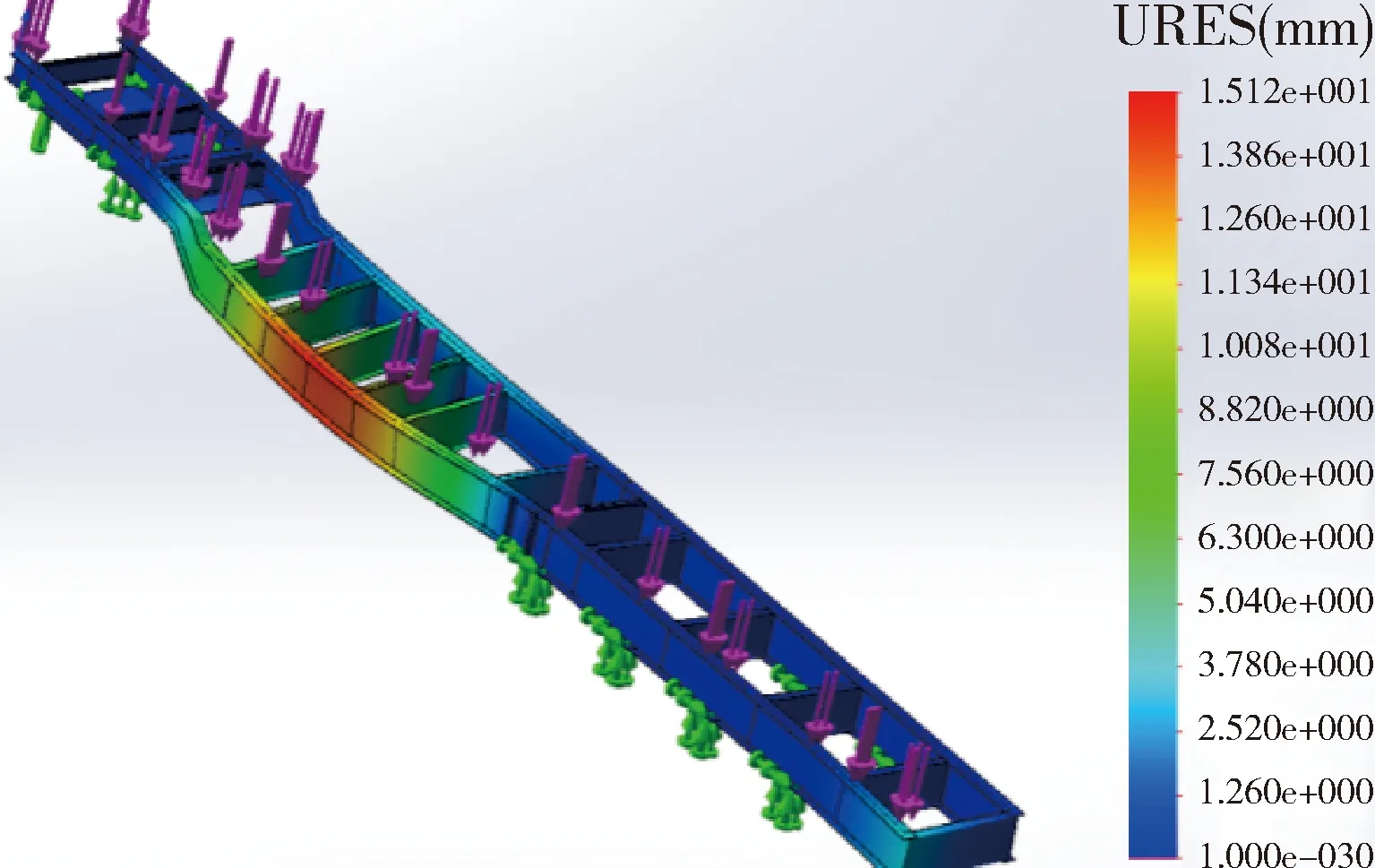
图10 位移云图(扭转工况)

2.3 制动工况

半挂车由于外部状况，会出现紧急刹车制动的情况，此时半挂车车架会受到装载的货物的压力和车辆本身重力的作用，以及它们沿着车辆行驶方向产生的惯性力作用.由于在行驶过程中各个车轴的轴荷是不同的，因此，制动时不同车轴的轴荷会产生较大改变，造成车架内部的纵横梁的内应力也发生较大改变.制动时按照各个车轮是同时间发生抱死现象的情况来进行计算，需要在半挂车行驶方向(纵向)上施加一个加速度去模拟制动工况的情况.按车架产生的最大附着系数为0.7来计算，则在X轴方向获得的制动加速度为-0.7 g.制动工况约束条件为：车架牵引销滑板处施加X、Y、Z三个方向的全部约束，在车架后部固定支架和吊耳处也实施X、Y、Z三个方向的全部约束.施加约束和力的情况如图11、12所示.

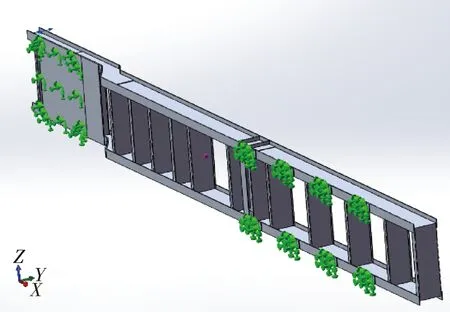
图11 制动工况约束示意图

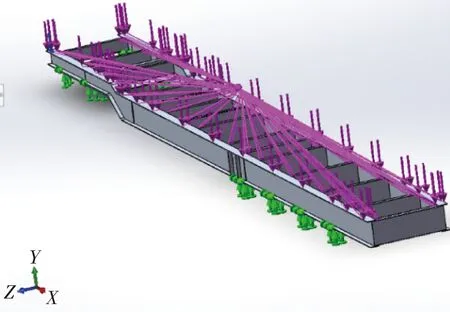
图12 制动工况载荷示意图

根据车架应力分布图13可知：制动工况也与扭转工况、弯曲工况类似，在牵引板与车架纵梁的连接部分会产生较大的应力集中现象，获得的最大等效应力(VonMises)为114 MPa，小于车架材料的屈服极限，认为强度合格.制动时产生的惯性力(纵向)会使车架后部产生较大的应力分布变化，而前端应力分布变化较小.图14可以看出车架产生的最大变形量为13.58 mm，最大变形处同样是发生车架受力时中前部没有支撑的部分，在惯性力(纵向)的作用下，车架的后段也明显的产生了一定位移.

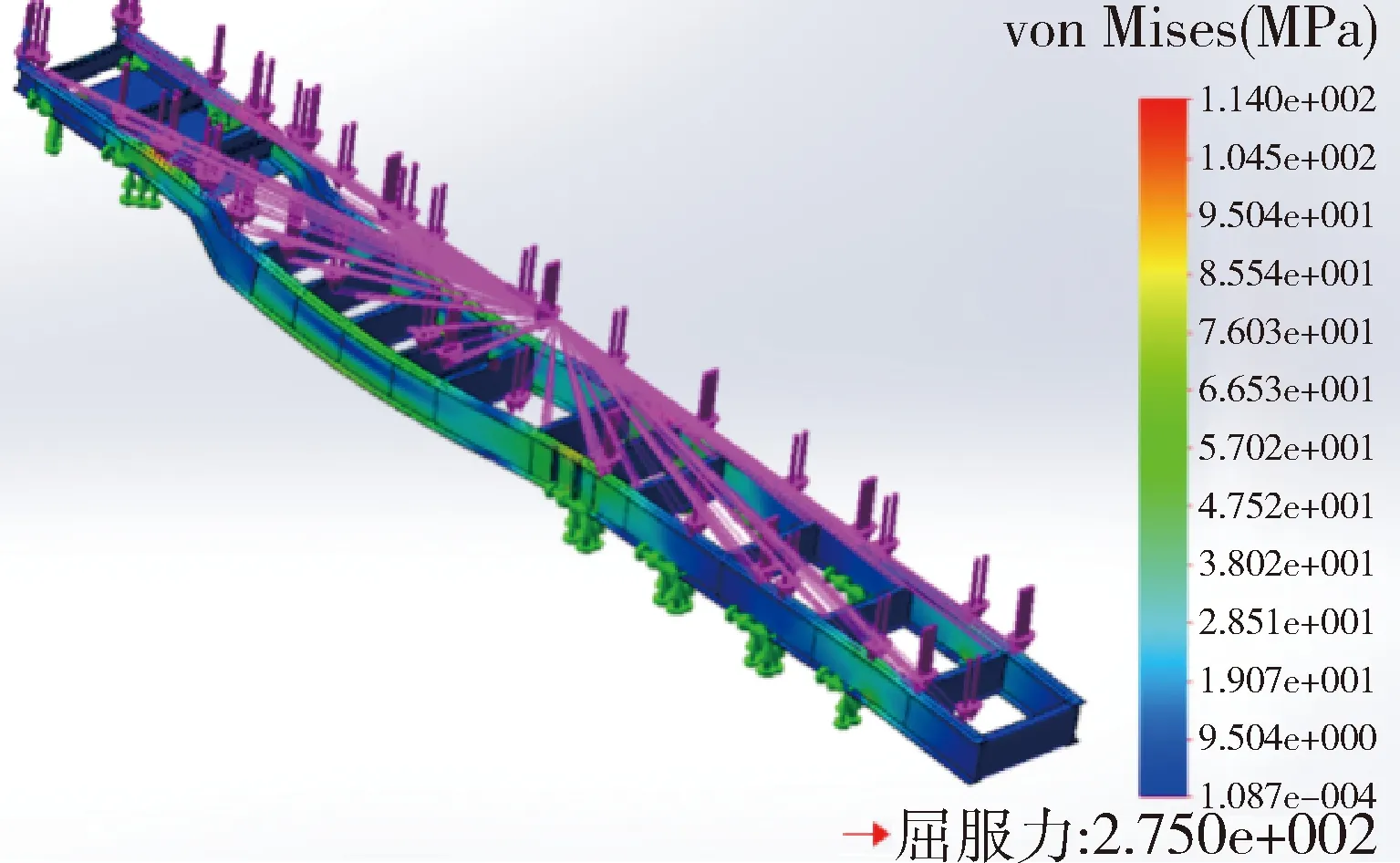
图13 应力云图(制动工况)

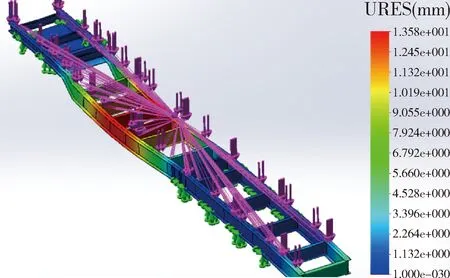
图14 位移云图(制动工况)

2.4 转弯工况

车辆在正常行驶过程中需要经常转弯，因此，转弯工况也是一个需要研究的特殊工况.在整个转弯工况过程中，车架需要承受来自装载货物的压力和自身的重量，由于转弯过程类似圆周运动过程，所有车架还要承受离心力的作用.在分析过程中，用一个侧倾载荷来代替离心力的作用，侧倾载荷会使几个车轴承受的垂直载荷发生突变，最终导致车架的应力、应变发生变化.载荷情况除同弯曲工况外，在Z正方向上加载0.4 g的离心力.转弯工况约束条件为：车架牵引销滑板处施加X、Y、Z三个方向的全部约束，在车架后部固定支架和吊耳处也实施X、Y、Z三个方向的全部约束.施加约束和力的情况如图15、16所示.

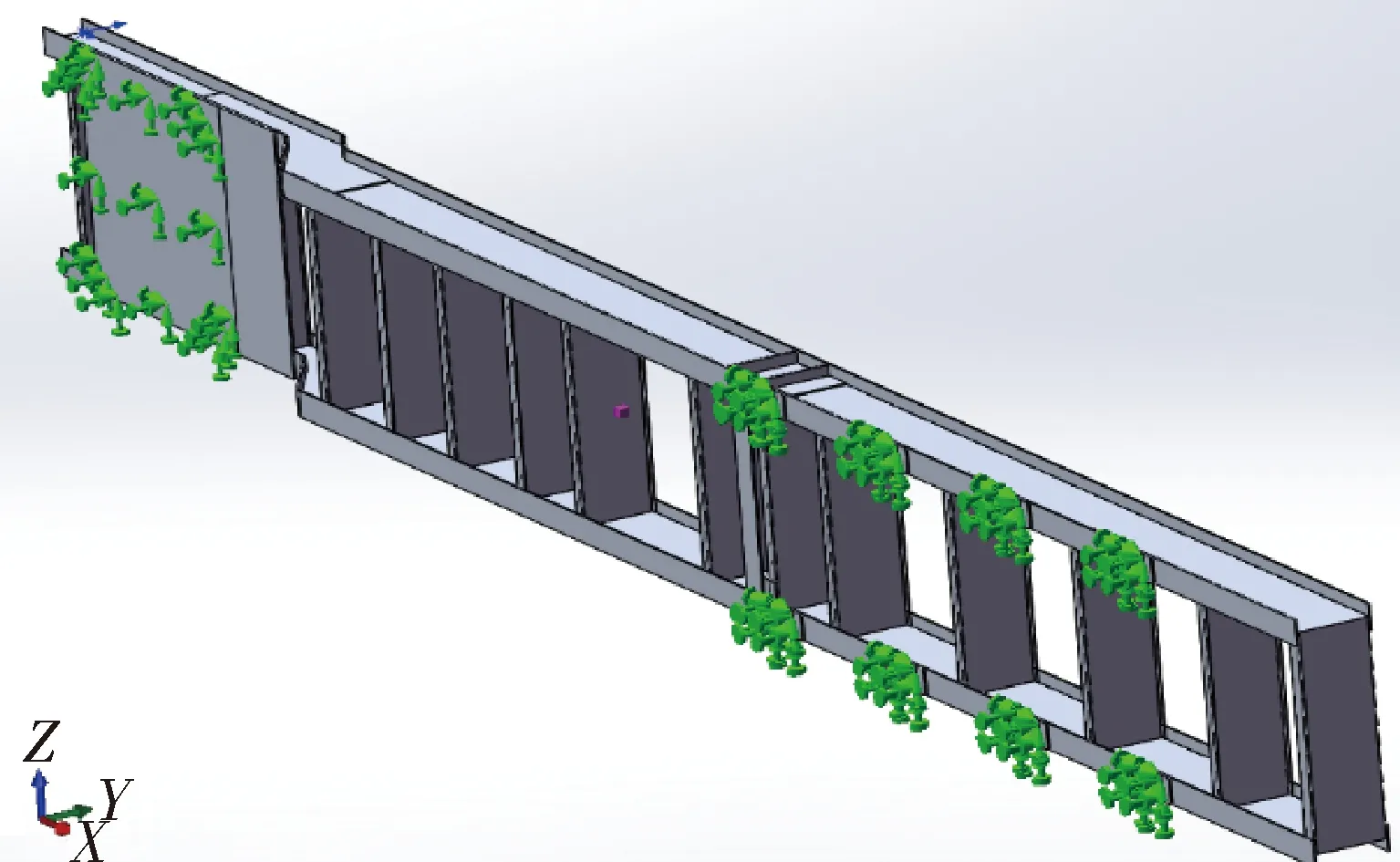
图15 转弯工况约束示意图

从图17可以看出:车架的等效应力(VonMises)最大值为155.7 MPa，小于铝合金车架材料的屈服极限，认为强度合格，所示的应力最大值出现在牵引板与车架纵梁的连接部分.另外，纵梁最后悬挂安装处的应力值也比较大且集中.从图18可以看出：车架因变形产生的位移最大量为18.57 mm，小于规定值(20 mm)，最大变形处同样是发生车架受力时中前部没有支撑的部分.转弯过程中，由于离心力的存在会使车架在左右方向上产生明显的位移现象.

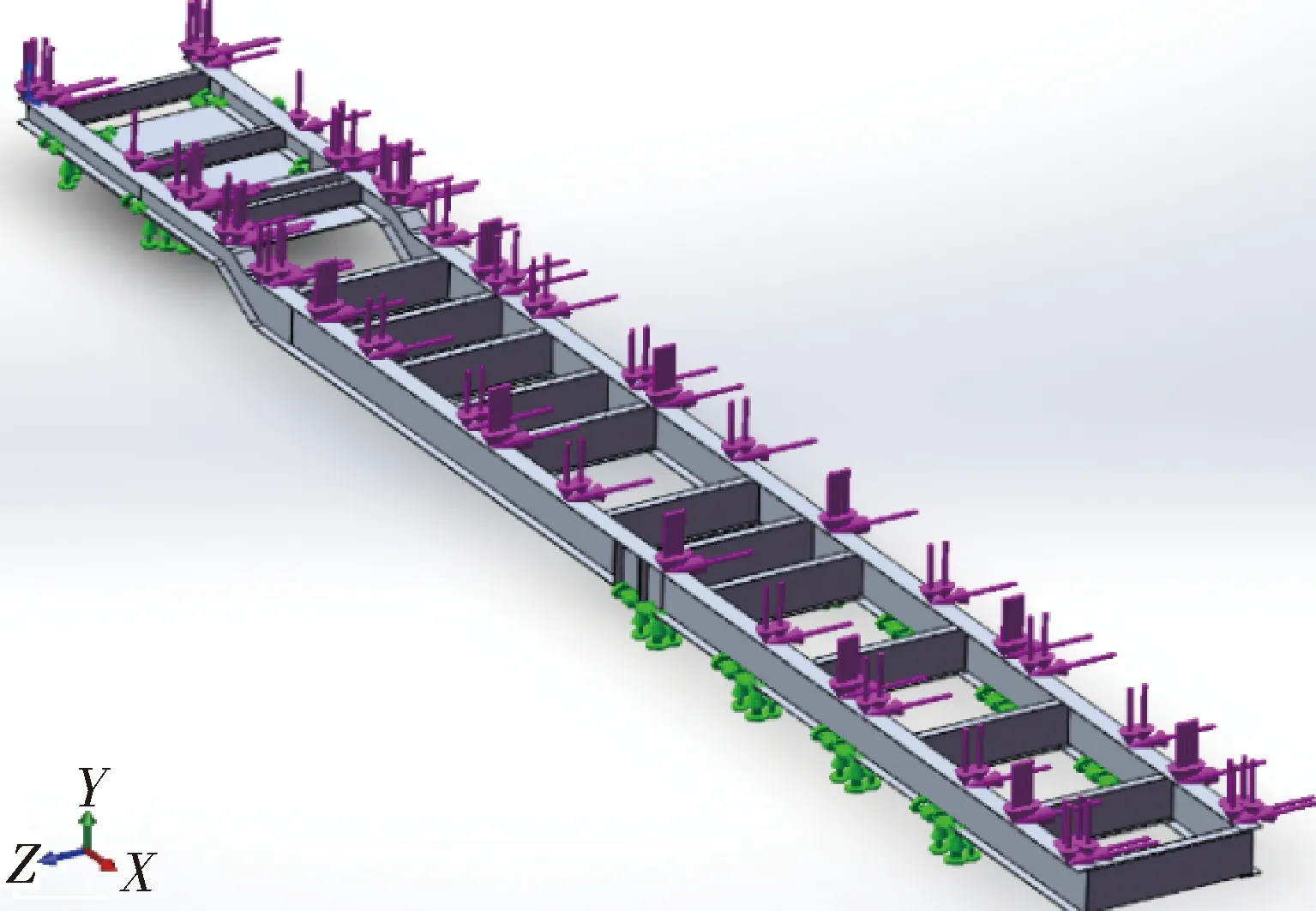
图16 转弯工况载荷示意图

图17 应力云图(转弯工况)

图18 位移云图(转弯工况)

2.5 数据分析

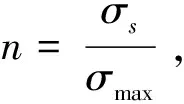
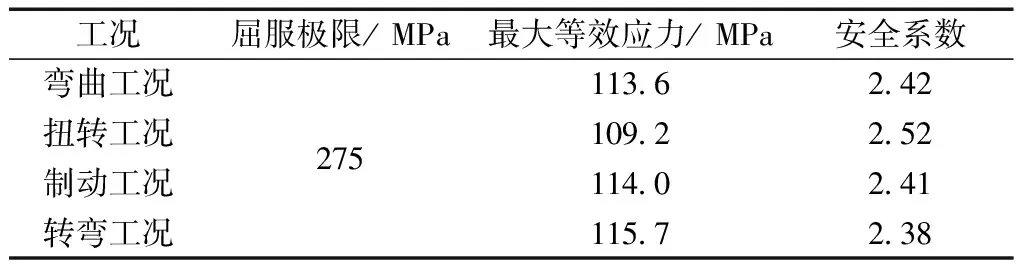
表1 各工况最大应力和安全系数

3 模态分析

模态分析是分析结构振动的一种常用方法，它主要研究的对象为某结构的振型和本身固有频率[12].要想设计出合理的车架结构，使其振动频率不在共振的频率范围内，就必须通过车架模态分析结果，去预测外部激励和该车架设计结构之间的相互影响.由模态分析结果可知，车架结构的前6阶是刚体模态，模态频率值为0，没有分析研究的实际意义.车架结构后10阶模态的固有频率和振型如表2、图19-23所示.

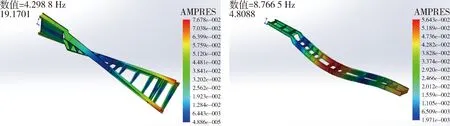
图19 第7阶和8阶振型图

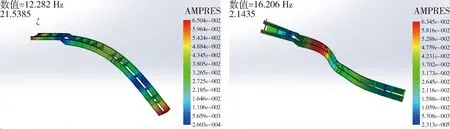
图20 第9阶和10阶振型图

图21 第11阶和12阶振型图

图22 第13阶和14阶振型图

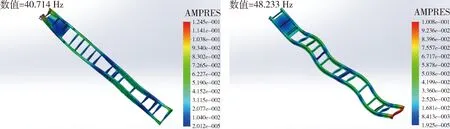
图23 第15阶和16阶振型图

表2 固有频率和振型特征

由固有频率可以知道：

(1)车架的16阶模态较为分散地分布在0～50 Hz频率带中，车架结构模态频率无突变现象，频率值分布比较分散，这样可有效避免与外部激励频率重合而引发共振.

(2)半挂车在行驶过程中，一般认为车架的固有频率是10～15 Hz[13-14]，而该车架的第7阶扭转和第8阶横向弯曲模态不在这个频段范围内，因此,车身不会产生较大幅度振动现象.

(3)骨架车行驶在各种路况上，其路况条件不同也会对车辆产生不同的外部激励，在较平坦公路或高速路上，车架受到的外部激励在1～20 Hz之间，并且多为垂直振动[15].在分析中得到，第12阶为垂直弯曲频率，其频率值不在此外部激励范围之内.故不会由路面的外部激励引起车架大振幅共振现象.

(4)第15阶和16阶在车架后侧局部模态变化幅度较大，模态较多，显示刚度较弱，因此,在车架后侧局部范围内可能产生疲劳破坏.

(5)半挂车正常行驶时，主车发动机的工作频率一般在48-52 Hz之间，除了第16阶模态频率比较接近之外，其它阶的模态都远低于发动机的工作频率.

综上所述，该车架正常行驶时，无大幅度振动现象产生，也不会产生共振现象，说明结构设计合理.

4 结 论

通过对某骨架车车架建立三维模型，根据静力学有限元分析原理，对车架模型在4种特殊工况(弯曲(满载)、扭转(满载)、紧急制动及转弯)下进行了静力学有限元分析，获得了该车架模型的位移和应力分布情况，验证了车架的刚度和强度是符合要求的.根据有限元模态分析原理，对车架三维模型进行有限元模态分析，预测外部激励和该车架设计结构之间的相互影响，获得了该车架1-16阶的模态频率和振型特征，验证了车架在正常行驶过程中无大幅度振动和共振现象的出现.此种分析方法为机械企业快速研发生产新车型提供了可靠的依据.