基于虚拟样机技术的履带车辆扭力轴载荷谱的编制

杨 慧， 白恩军， 黄树涛， 韩 尧

(沈阳理工大学 汽车与交通学院，沈阳 110000)

履带车辆的工作环境极差，使用场合特殊，且车辆工况复杂.其扭力轴是悬挂系统的减震装置，是悬挂装置的主要弹性元件[1].车辆的扭力轴部分主要起到减震缓冲的作用.当路面环境恶劣时，路面颠簸，路面激励传递到负重轮，通过平衡轴传递到扭力轴，这时发生弹性扭转，车辆可以保持平稳行驶.为了符合工作目标及要求，使得履带车辆在行驶过程中的行动部分有足够的可靠性，则扭力轴可靠性要达到标准.载荷谱是车辆机械结构设计的依据，它是各机械结构寿命计算及延长、动力学仿真和有限元分析等计算机计算设计必不可少的条件[2].抗疲劳设计领域的实践证明，应用载荷谱能够加速零部件的研发和验证过程，可有效提高零部件的疲劳寿命和可靠性水平.目前在载荷谱的获取方法上，针对普通车辆，沈磊等[3]用常规的半解析方法，利用实际车辆试验，获得主轴的载荷来做车辆模型的激励，这样的方法优于虚拟试验场，但计算负荷缺乏测量精度，边界条件的通适性较弱,且验证困难；卞学良等[4]使用虚拟迭代的方法，采用真实试验系统载荷为目标信号，这样的载荷精度较半解析法高，但计算量较大；Kang等[5]使用虚拟试验场，在模拟道路上“启动”车辆模型.该技术全部采用的虚拟模型，所以在车辆早期研发就能介入，计算载荷精度较高，也可以采用实际试验进行试验验证，但也可能会产生难以通过实物测试验证的错误负载，而且对于轮胎的模型精度要求很高.针对于履带车辆，魏领军等[6]人运用档位分割和档位里程统计得到载荷，采用极大值统计规律编制载荷谱，这样的方法考虑到了车辆总设计里程和轴转矩载荷信息的不确定性，但是理论复杂，对样本空间容量要求较大，受较强局限性.

因此，文中将以履带车辆为研究对象，利用虚拟样机技术建立整车模型，根据实际情况创建任务剖面，用“车辆-车架”试验系统进行虚拟实验，节省时间和物力，得到的载荷谱采用雨流计数法和载荷函数法处理，编制出实用的扭力轴载荷谱，为进一步优化扭力轴结构和性能提供数据支撑，总结规律，为后期履带车辆等大型机械设备研究可靠性过程中出现的问题提供参考数据.

1 履带车刚柔耦合模型建立

在Adams软件内，可建立履带车辆行驶系统的虚拟样机[7].在Adams ATV插件中建立履带车辆模型，扭力轴部分暂用弹性元件代替，再运用有限元软件建立扭力轴的柔体模型.扭力轴的组成一般分为3部分，主要部分为扭力轴的直杆部分、两端花键部分和花键与直杆的过渡部分.建立柔性体模型最重要的部分为网格划分，这里采取四面体网格划分.为了减少有限元分析计算的规模，对扭力轴的花键、端面倒角处等对分析影响不大的部位简化，如图1所示.

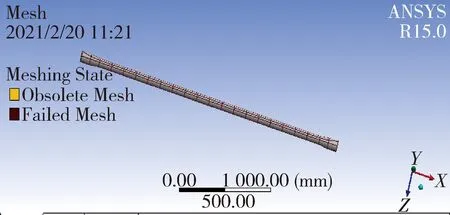
图1 扭力轴网格划分

导入网格划分后的扭力轴柔性体文件，将ADAMS插件中的履带车刚体模型的扭力轴花键安装部位的约束以及负重轮和刚性连杆弹簧力删除.将扭力轴柔性体移动到刚体模型中对应的位置，将车体和平衡轴与扭力轴的两端花键建立固定副约束.最终的履带车辆刚柔耦合模型如图2所示.

图2 履带车辆整车刚柔耦合模型

2 履带车辆行驶虚拟实验

2.1 随机路面模型建立

按照路面轮廓可以将路面分为规则路面和随机路面(roughness).规则路面是可以确定的固定形态的路面，如正弦路面、凸起路面等；而随机路面具有随机性，无法用函数定义，如碎石路面、标准公路面、田野路面等.这类路面虽然无确定函数，但是具有方差、相关函数、功率谱密度、均值等参数规定.

ADAMS中提供了一些规则路面，为了满足实验任务剖面要求，需要重新建立用于动力学仿真的路面模型.随机路面是ADAMS中的一个路面生成插件，基于Sayers数字模型，可创建多种道路测试的经验模型[8].

路面功率谱密度是定义Sayers数字模型的主要参数，国际标准的功率谱密度函数的公式[9]为

(1)

式中:ω为频率指数，通常取2；n为空间频率，表示每米长度中包括的波长数量，m-1；n0为参考空间频率，通常取0.1 m-1；Gq(n0)为路面不平度系数，m2/m-1.

根据国际规定的标准路面不平度系数，可以将路面分为A—H等八个等级[10]，如表1所示.A为高速公路；B、C为沥青路和水泥路；D为未铺装路面和土路，E为未铺装路面的损坏路面和碎石路面；F为田野；G为未铺装的不平路面和被车辆碾压损坏的路面.

表1 基于国际不平度指数的路面等级分类

为了实现ADAMS中道路模型的建模，需要将空间功率谱密度函数进一步转化为速度和加速度的功率谱密度函数，国际标准中规定，他们的关系式[11]为

Gs(n)=(2πn)2Gq(n)，

(2)

Ga(n)=(2πn)4Gq(n).

(3)

式中:Gs(n)为速度功率谱密度，m；Ga(n)为加速度功率谱密度，m-1.

波长取5 m，功率谱密度数据结果如表2所示，作为后续路面类型建模的数据依据.

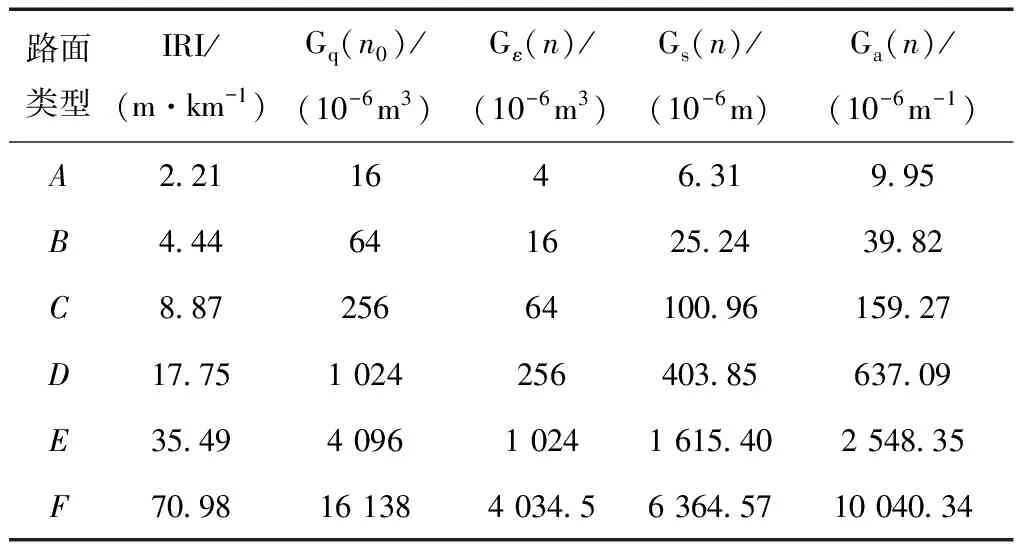
表2 功率谱密度计算数据

2.2 任务剖面的建立

建立的载荷谱能否应用于履带车辆扭力轴疲劳寿命研究，重点是任务剖面是否符合履带车辆的实际使用工况.因此,建立载荷谱的基础是设置合理的任务剖面.履带车辆标准试验里程为10 000 km，履带车辆行驶路面分配百分比,以及履带车辆行驶速度分配百分比是确定履带车辆任务剖面的基本参数[12].行驶工况建模时，考虑到的操作包括直行、爬坡、制动、加速、减速.统计大量实验数据，按路面和速度分配比例设计试验路面，如表3所示.C路面不平度较小，速度适应性较强，E路面不平度高，无法达到高速行驶.

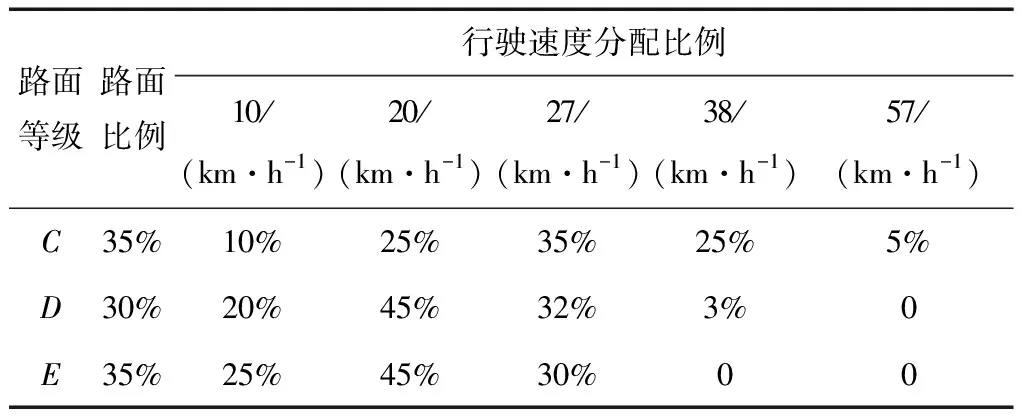
表3 试验路面分配比例

2.3 实验设计

为了节省仿真运算时间，同时保证可以反映车辆实际承受载荷的真实情况，进行虚拟实验时，针对于3种路面，每种工况只进行50 s，按照各工况在任务剖面中所占的百分比，叠加各工况的载荷，最终得到代表10 000 km里程的目标载荷.

3 载荷的处理与载荷谱的编制

随机载荷不利于后续的方案设计和进一步的疲劳试验，若将得到的载荷极值乘以外推因子1.0～1.5，方法简单,但是,所得到的极值可能偏小.因此，将数据用雨流计数法[13]处理，得到每组载荷数据的均值和幅值，将其视为二维随机变量，采用载荷函数法[14]，拟合出均值和幅值的独立分布，将雨流矩阵中相同幅值和均值的频次分别求和，从而得到各工况的载荷频次关于均幅值的独立分布结果，如图3-8所示.幅值满足对数正态分布，均值满足正态分布.

图3 C路面各工况幅值直方图

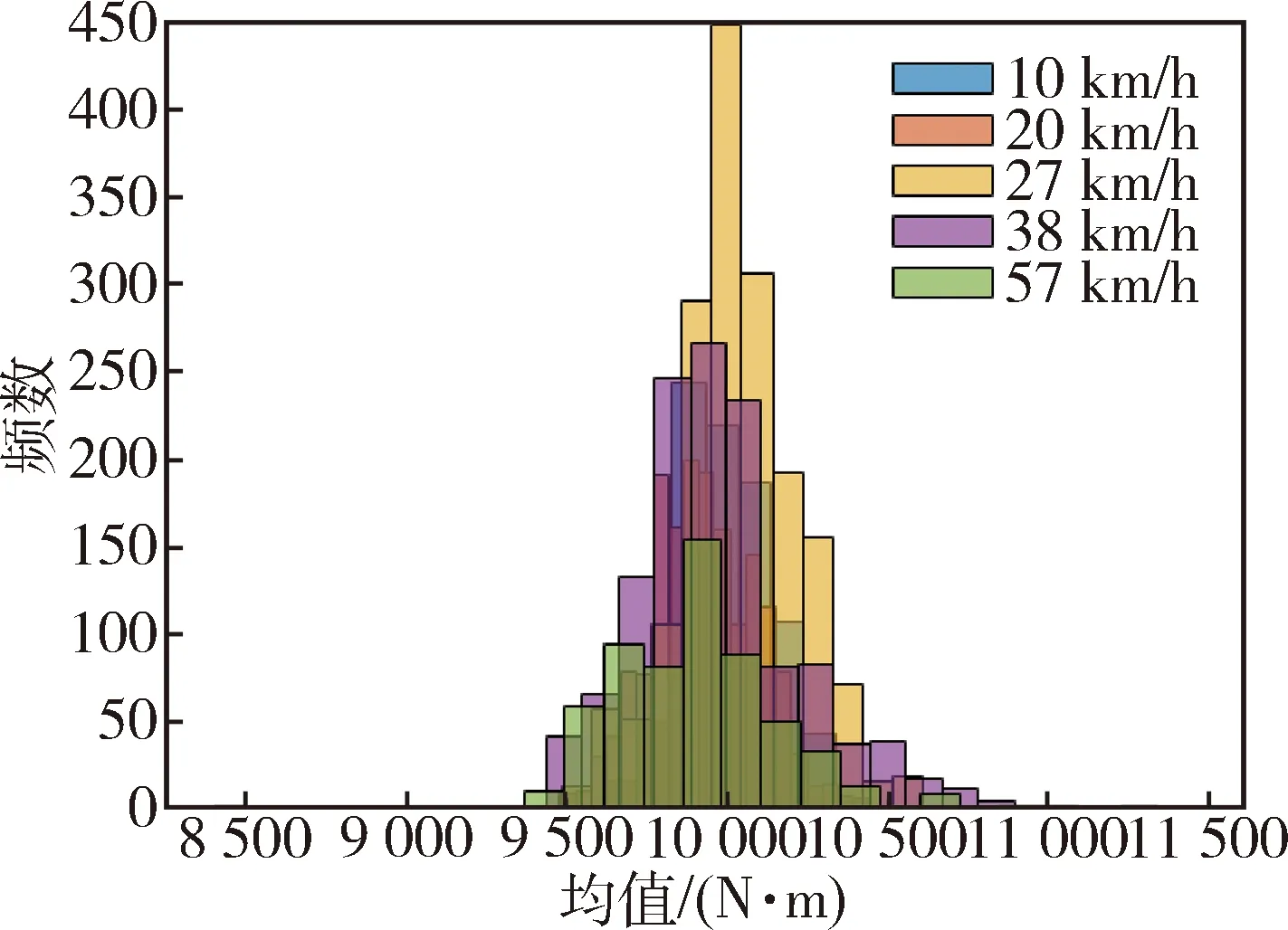
图4 C路面各工况均值直方图

图5 D路面各工况幅值直方图

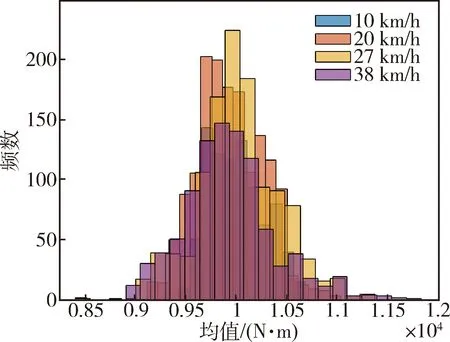
图6 D路面各工况均值直方图

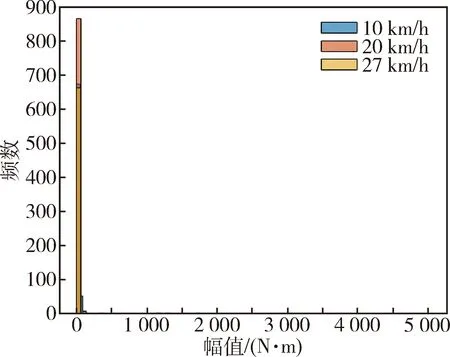
图7 E路面各工况幅值直方图

图8 E路面各工况均值直方图

通过观察分析可得到以下结论：各工况幅值的分布均呈单偏峰、右长尾形式，较稳定；均值的分布在恶劣路面较分散，在不平度较低的路面较一致，整体成正态分布；高速行驶工况使用频率低，载荷循环次数较少.

设载荷均值变量为X，载荷幅值变量为Y，载荷均值的正态概率密度函数表达式和载荷幅值的对数正态概率密度函数为

(4)

(5)

将载荷循环外推至106，得到均值的极大值推断公式为

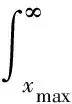
(6)

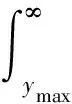
(7)

N0为外推累积循环频次，Nx、Ny为外推前均值和幅值的载荷频次.

则由上式的积分公式可得到各种工况下的载荷幅值和均值的极大值.文中载荷幅值的外推极值为29 165.2 N·m.

应用conover理论将载荷谱分为八级[15]，精确地反映其疲劳效应.划分方法为：第1级到第4级之间的差逐渐加大，第4级到第8级之间是等差的.设第1级为X1，则第2级到第8级分别为0.95X1、0.85X1、0.725X1、0.575X1、0.425X1、0.275X1、0.125X1.

采用线性疲劳累计损伤理论优化八级载荷谱，合成载荷—累计频次，将合成的载荷—累计频次按照疲劳损伤等效原则转变为阶梯状的八级扭矩载荷谱，如表4所示，其中,包括载荷级别、与之相对应的循环数和每次重复的循环数，该扭矩谱可用于疲劳加载.

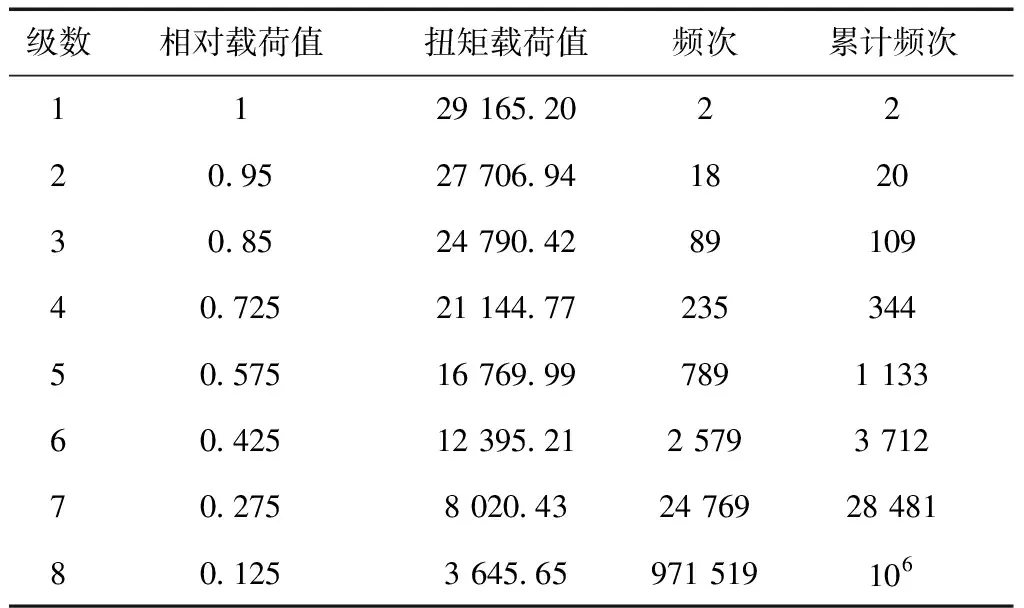
表4 扭力轴扭矩谱

4 结 论

结合虚拟样机技术和有限元方法，建立了履带车辆刚柔耦合多体动力学模型，并基于Sayers数字模型,建立了符合国标的仿真路面模型.根据任务剖面的划分规则，通过仿真获得了扭力轴随机载荷谱，应用conover理论和统计分析方法，编制了扭力轴八级程序载荷谱.不仅实现了复杂试验模拟化，同时，也为扭力轴的设计、试验、疲劳寿命及可靠性研究提供了大数据支持.