具有年龄结构随机SIRS模型的持久性分析

刘娟，陈功

(蚌埠学院 理学院，安徽 蚌埠，233030)

通过数学建模的方法建立疾病传播模型称为传染病动力学。传染病动力学是生物数学的一个重要分支，利用数学方法对模型进行分析，可以显示传染病的流行规律，这对于传染病的预防与控制具有较重要的意义。近年来，传染病动力学受到了国内外学者的广泛关注，不同类型的传染病模型被提出[1-5]，文献[6]研究了具有年龄结构的SIRS传染病模型：

(1)

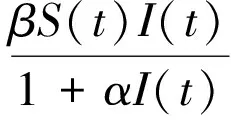
模型式(1)为用微分方程表示确定型模型，没有考虑随机干扰，在确定型模型中加入随机扰动项可以得到随机生物模型，这也是生物数学的一个研究热点[7-9]。与确定型模型相比，随机干扰可以使模型的许多性质发生变化，因此，考虑外部干扰，本文在模型(1)中加入随机扰动项，用白噪声来表示。外界白噪声对模型的影响有多种，本文假设白噪声影响参数为β，此处β为接触率，即βdt→βdt+σdB(t)。其中，B(t)为标准布朗运动，σ2为白噪声强度。引入白噪声后得到随机模型式(2)，本文主要研究随机模型式(2)中I(t)和R(t)的持久性。

(2)

将模型式(2)的等式两边相加，可以得到

d(X+S+I+R)=[A-μ(X+S+I+R)-εI]dt

≤

[A-μ(X+S+I+R)]dt

对于d(X+S+I+R)=[A-μ(X+S+I+R)]dt，由初始条件可得

(3)

为模型式(2)的正不变集。为了研究方便，假设(X(0),S(0),I(0),R(0))∈Γ*。

1 I(t)和R(t)的持久性

生物系统的持久性，指的是系统中的某一类群体在一定时期内能够持续生存、不会出现灭绝现象，利用数学符号可以定义持久性含义[10]。设f(t)为生物系统中的某一群体，规定两类持久性的含义如下：

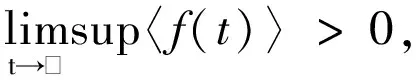
定理1 设Y(0)=(X(0),S(0),I(0),R(0))为模型(2)的初始条件，若白噪声强度满足

则模型(2)的解I(t)满足：

其中

，

证明在模型(2)两边取0到t的积分，并除以t，得到

(4)

有

=

解得

(5)

其中:

由式(3)可知

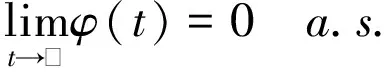
(6)

=

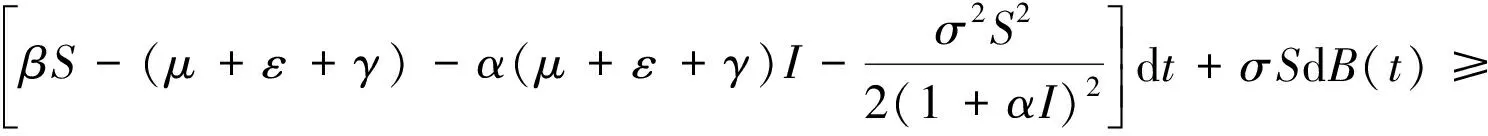
(7)

对式(7)两边取0到t的积分并除以t，利用式(5)结果，得

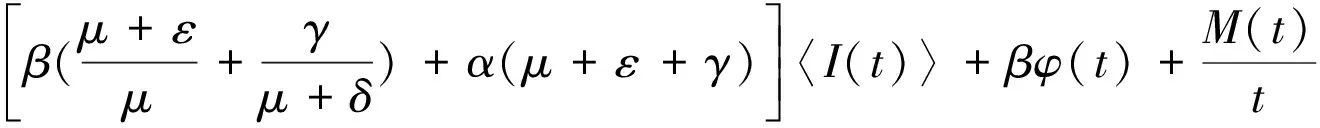
(8)

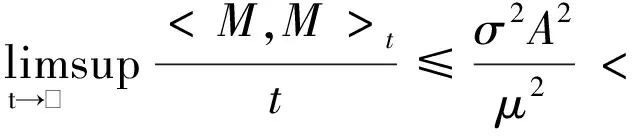
由强大数定律可知

(9)

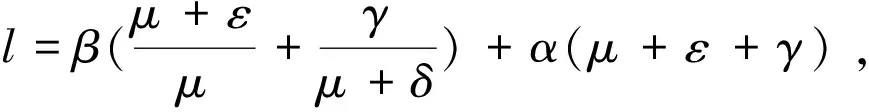
(10)

(11)

对上式两边再取0到t的积分，并除以t，将〈S(t)〉的结果代入，得

(12)

由式(6)易知

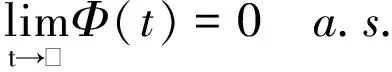
(13)

(14)

由式(11)和式(14)可得定理(1)。

。

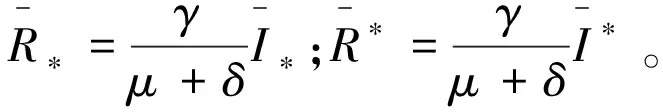
2 结论

在一类具有年龄结构SIRS传染病模型的基础上，加入随机扰动项，研究了一类随机SIRS传染病模型的持久性。利用It公式及强大数定律得到了I(t)和R(t)持续存在的充分条件。结果表明，当白噪声强度σ2不太大且满足一定条件时，〈I(t)〉和〈R(t)〉将在一定范围内取值，即模型中的疾病会持续存在，不会消失，这对于传染病的预防与控制是不利的。