基于EMI技术的小型直流电机的机械噪声控制

张军 ，周德威 ，赵林玉

(1.安徽理工大学 机械工程学院，安徽 淮南，232001；2.安徽理工大学 人工智能学院，安徽 淮南，232001)

小型有刷永磁直流电机由定子和转子两部分组成，在定子和转子之间存在气隙。电机的定子由壳体、永磁体、轴承等部件组成，电机的转子则由转子铁心、绕组、换向器(又称整流子)和轴承等部件构成。在正常情况下，在电机工作过程中定子和转子同时振动，如果它们的模态频率很接近(相差在±6%范围内)就会出现共振现象，产生极大的噪声[1]。因此，如何错开定子和转子的固有频率，消除电机共振的可能，直接决定了电机机械噪声的控制效果。在建模过程中发现定子结构相对简单，而转子模型比较复杂[2]。因此，本文在设计变量时通过改变定子的模型参数来减少不必要的实验误差。

1 电机振动理论

1.1 电机振动噪声的来源

随着机电设备的发展，电机的应用也越来越广泛，电机的振动噪声也随之引起人们的关注，其振动噪声主要分为电磁噪声、机械噪声、空气动力性噪声3部分[3]。本文主要研究小型直流电机的机械噪声。电机的机械噪声主要是运转部分的摩擦、撞击、不平衡以及结构共振形成，主要由轴承和换向器引起[4]。电机轴承在繁重的工作状态下运转时，滚珠和外圈滚道相接处会发生弹性变形，滚道变形随接触处的变化呈周期性变化，产生振动和机械噪声。

1.2 电机振动模型

电机噪声的来源主要是由机械振动产生。在电机的内部，振动主要由电磁力产生。在建立电机的振动模型时，可以将电机视为一个机械系统，根据系统的自由度、质量、刚度等参数，电机内部的电磁力以及电磁力的各种分量对系统的振动都有影响，依据振动方程，建立系统的数学振动模型为[5]

(1)

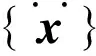
[C]=a[M]+b[K]

(2)

在确定系统的阻尼矩阵后，利用特征方程求出微分方程组，从而得到各阶振型的振动频率，振幅的相对值为

将[P]正则化后，解耦后的振动激励源F(t)的表达式为

F(t)=F0ejwt

(3)

通过求解非齐次微分方程，得出振动方程的解为

x=e-δt(Aejw0t+Be-jw0t)+εejwt

(4)

式中得出e-δt(Aejw0t+Be-jw0t)为瞬态响应；εejwt为稳态响应。

在实际计算中，系统中的阻尼十分复杂，需要通过引入复数形式的模态系数，即复模态理论，且需要引入辅助方程如下式所示：

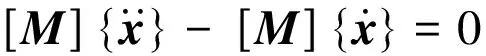
(5)

多自由度的振动方程式的表达式为

(6)

式中：ηir为指点i的r阶模态系数；γir为指点i的r阶的模态相角；Pr为模态坐标幅值；θr为模态坐标相角；αr为复模态频率实部；βr为复模态频率虚部。

2 压电阻抗(EMI)技术

2.1 压电效应

压电效应是压电材料在电场的作用下发生极化现象，内部电荷发生移动。去除电场后，压电材料内部仍存在极化电荷，这使得压电材料具有了压电效应。当有力加在压电元件上时，将引起压电元件内部电荷发生相对运动产生电信号，这种将压电材料由机械能转换成电能的现象称为正压电效应。相反，在压电元件表面上施加电压，导致压电元件的机械变形，这种将压电材料由电能转换成机械能的现象称为逆压电效应。压电阻抗技术就是运用了压电的逆效应现象[6]。

2.2 机械阻抗

系统的机械阻抗可以简化为“弹簧-质量-阻尼系统”，又称SMD系统。为阐述结构压电耦合的动态响应，通过单自由度SMD系统分析其动态特性，见图1。

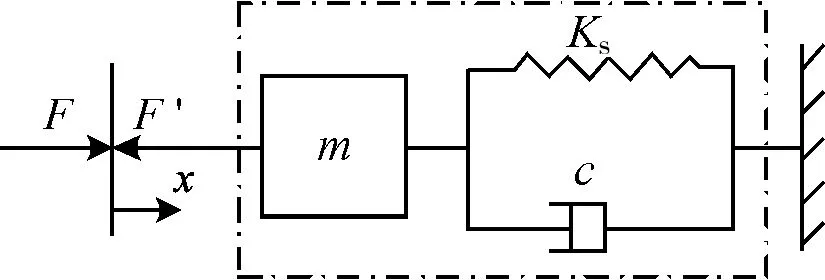
图1 结构机械阻抗图Fig.1 Structural mechanical impedance diagram

该结构的机械阻抗ZS可以表示为

(7)

系统的激振力F，机械阻抗ZS和响应位移X的关系表示为

(8)

系统动态刚度KD表示为

(9)

F=-KDX

(10)

式中：c为系统阻尼，N·mm/s；m为系统质量，g；ω为激振频率，Hz；ωn为系统谐振频率，Hz；j为虚数单位。

2.3 结构压电耦合电阻抗原理

PZT-4压电陶瓷片既做接收器又做发射器，因此,选择PZT-4。PZT-4与单自由度SMD系统进行结构压电耦合对压电耦合后电阻抗原理进行阐述[7]，见图2。

PZT-4的电阻抗Z的表达式为

(11)

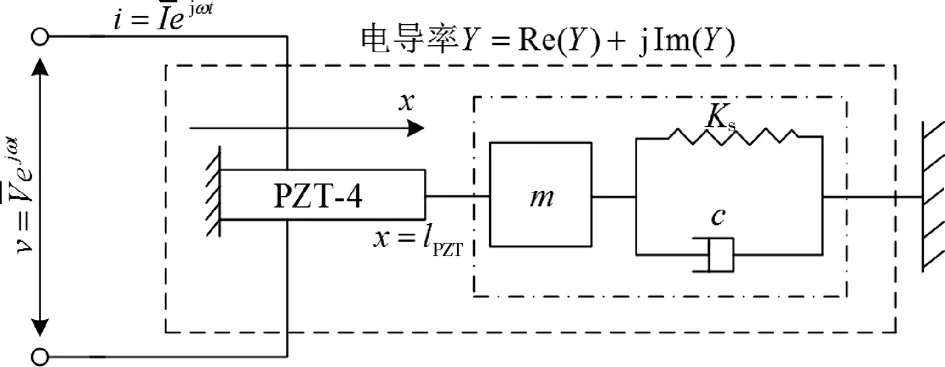
图2 PZT-4与单自由度SMD系统耦合模型图Fig.2 Coupling model of PZT-4 and single-degree-of-freedom SMD system

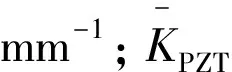
通过公式推导，结构压电耦合后电阻抗与PZT-4片尺寸、自身机械阻抗、结构机械阻抗、激振频率都存在一定的关系[8]。

3 仿真与模拟实验

3.1 转子的模态仿真分析

仿真前需要建立电机转子的三维模型，小型有刷永磁直流电机转子的建模材料及参数见表1。

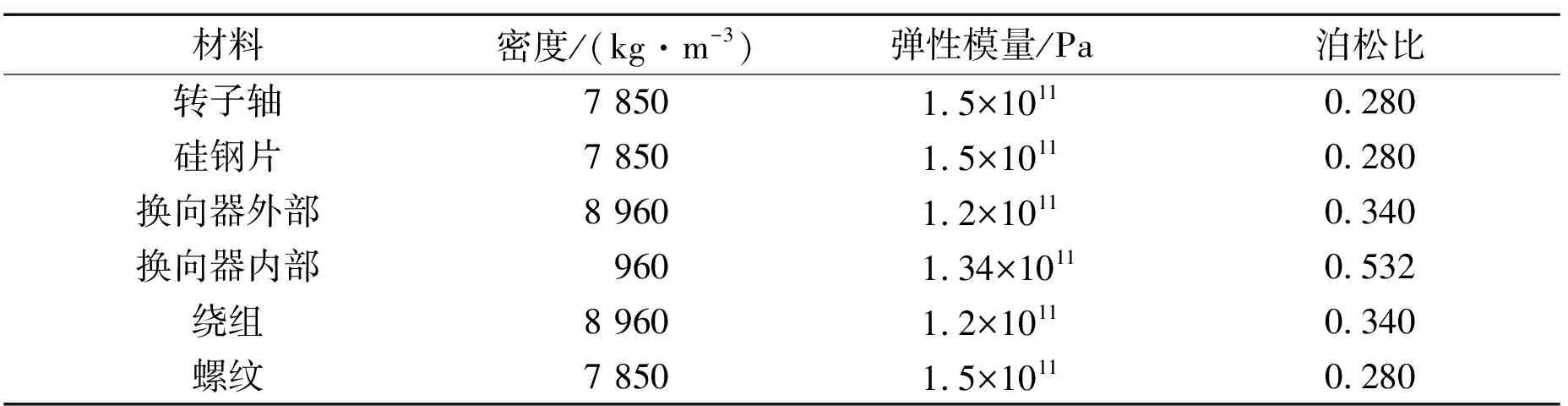
表1 小型有刷永磁直流电机转子材料表Table 1 Material table of the rotor of a small brush permanent magnet DC motor

将电机转子模型导入ANSYS WORKBENCH的压电模块，进行谐响应分析，在大面积扫频发现，转子频率在4 000～16 000 Hz时位移量明显较大，故研究区间为4 000～16 000 Hz得到转子的前30阶模态结果见表2。

表2 转子30阶模态表Table 2 30th order modal table of a rotor

本文需要仿真得到转子的固有频率，用ANSYS WORKBENCH分析转子的压电仿真图形，见图3。

图3 转子压电仿真图形Fig.3 Piezoelectric simulation graph of a rotor

由转子的压电仿真图可知:转子在6 640,10 560,12 080和14 160 Hz时位移较大，可知这4个频率点是转子的固有频率。

3.2 定子模态的仿真分析

仿真前需要建立定子的三维模型，小型有刷永磁直流电机的定子建模材料及参数见表3。

表3 定子材料表Table 3 Material table of a stator

将电机定子模型导入ANSYS WORKBENCH的压电模块，进行谐响应分析，同理得转子的前12阶模态(区间为4 000～16 000 Hz)结果见表4。

表4 定子12阶模态表Table 4 12th order modal table of a stator

同理，本文也需要仿真得到定子的固有频率，用ANSYS WORKBENCH分析定子的压电仿真图形，见图4。

由定子的压电仿真图可知:定子在4 360，6 040，9 520，10 240，11 560，14 800和15 520 Hz时位移较大，可知这7个频率点是定子的固有频率。

3.3 模拟实验及分析

由文献[5]知电机的共振带为±6%。由转子的压电仿真图可知：转子的固有频率为6 640，10 560，12 080和14 160 Hz。对应的共振带分别为[6 241.6，7 038.4]，[9 926.4，11 193.6]，[11 355.2，12 804.8]和[13 310.4，15 009.6]Hz。将共振带与转子压电仿真图对比可知：定子与转子在工作中存在共振现象，且在转子频率点为10 240，11 560和14 800 Hz时可能产生共振。由于定子结构相对简单，而转子结构复杂。在设计变量时通过改变定子的模型参数减少不必要的实验误差。本文通过改变定子的厚度、材料、弹性模量和泊松比，从而改变定子的固有频率，减少电机在工作中产生共振的可能，从而减少噪声，达到降噪效果。

3.3.1 定子壳厚度对定子固有频率的影响实验

在保证其他因素相同的条件下，改变定子壳的厚度，验证定子壳的厚度对定子固有频率的影响，仿真实验中将定子的定子壳厚度分别设置为2.0，2.2，2.4，2.6，2.8和3.0 mm。由模态仿真实验得出前6阶固有频率，见图5。

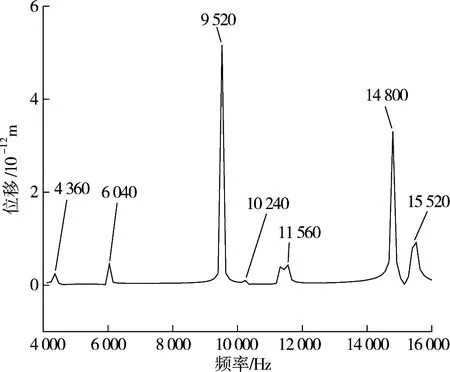
图4 定子压电仿真图形Fig.4 Piezoelectric simulation graph of a stator

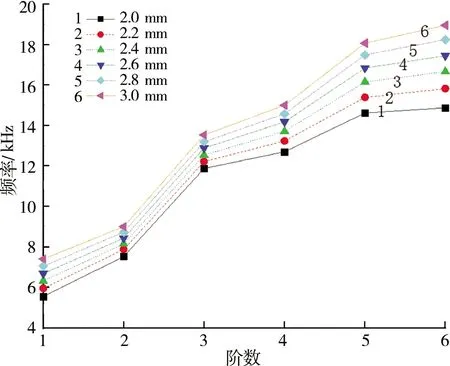
图5 定子壳厚度对定子固有频率的影响Fig.5 Influence of shell thickness of a stator on its natural frequency

由图5可知，定子的固有频率受定子壳厚度影响，且定子的固有频率随着定子壳厚度的增加而增大。

3.3.2 定子材料对定子固有频率的影响实验

在保证其他因素相同的条件下，仅改变定子壳材料，验证定子壳材料对定子固有频率的影响。仿真实验中将定子壳材料依次设为铝合金、铸铁、钢、铜，材料的基本参数见表5。

表5 材料基本参数表Table 5 Table of basic parameters of materials

用以上不同材料参数去定义定子壳并进行模态仿真实验，由模态仿真实验得出前6阶模态频率，然后通过ORIGIN软件绘制出图形，见图6。

从图5可知：材料的固有频率顺序为钢、铝合金、铸铁、铜。由表5可知：钢的密度、弹性模量、泊松比都不是最值，而固有频率为最大值。为验证出现这种现象的原因，设置如下3个实验来判断密度、弹性模量和泊松比对刚模态频率的影响。

实验1：设置定子壳材料为钢，保证其他因素相同，仅改变定子壳钢材料的密度，验证定子壳材料密度对定子固有频率的影响。仿真实验中，将定子壳材料密度依次设为2 880，7 350，7 850和8 960 kg/m3。对不同钢材料密度的定子壳进行模态仿真实验，由模态仿真实验得前6阶模态频率，然后，通过ORIGIN软件绘制出图形，见图7。

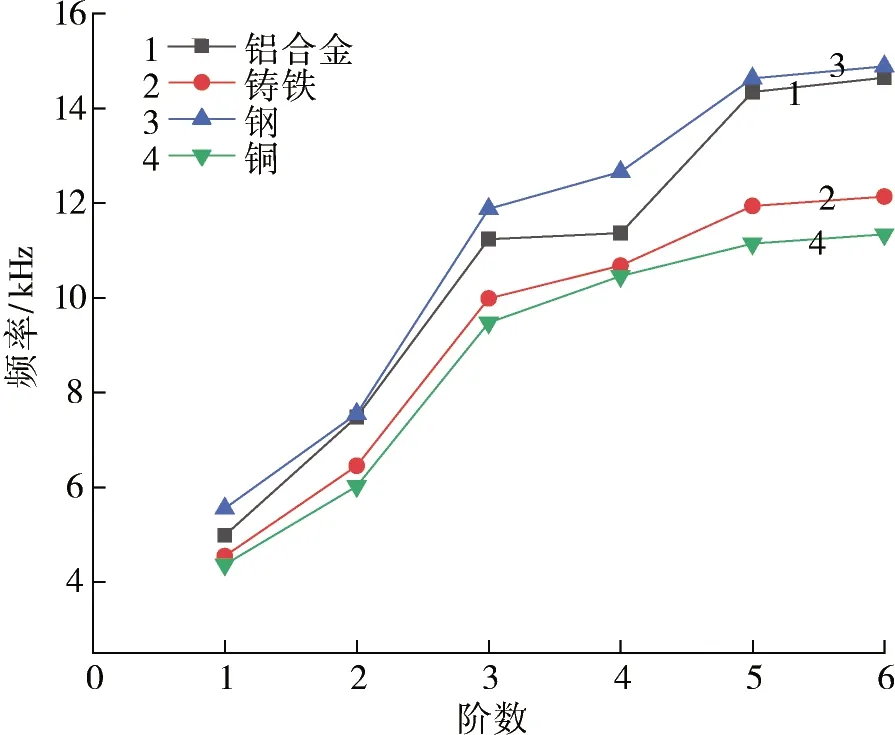
图6 定子材料对定子固有频率的影响Fig.6 Influence of material of a stator on its natural frequency

图7 材料密度对定子固有频率的影响Fig.7 Influence of material density of a stator on its natural frequency

由图7可知：定子的固有频率受材料密度的影响，随着材料密度增加，定子的固有频率减小，且改变定子的材料密度对定子固有频率的影响较小。可以得出：定子壳的材料为钢时，材料密度是导致出现最大值的因素之一。

实验2：设置定子壳材料为钢，保证其他因素相同，仅改变定子的弹性模量，依次设为70,120,150和200 Gpa。判断不同弹性模量对定子固有频率的影响。由模态仿真实验得出：前6阶模态频率，然后，通过ORIGIN软件绘制出图形，见图8。

由图8可知：定子的固有频率受弹性模量的影响，随着弹性模量增加，钢的模态频率也随之增大，改变定子的弹性模量比改变材料密度对定子固有频率幅度变化要大。可以得出：定子壳的材料为钢时，弹性模量可能是导致出现最大值的因素之一。

实验3：在保证其他因素相同的条件下，仅改变钢材料的泊松比，依次设为0.20，0.25，0.30和0.35。判断不同泊松比对钢模态频率的影响，由模态仿真实验得前6阶模态频率，然后，通过ORIGIN软件绘制出图形，见图9。

由图9可知，定子的模态频率在泊松比为0.2～0.35之间不受泊松比的影响，可以得出定子壳材料为钢时，泊松比不可能是导致出现最大值的因素之一，所以定子的固有频率为最大值的原因是密度和弹性模量。结合图7和图8可知：钢的固有频率为最大值的原因最有可能是弹性模量，因为弹性模量对定子固有频率带来的变化幅度远大于材料的密度。

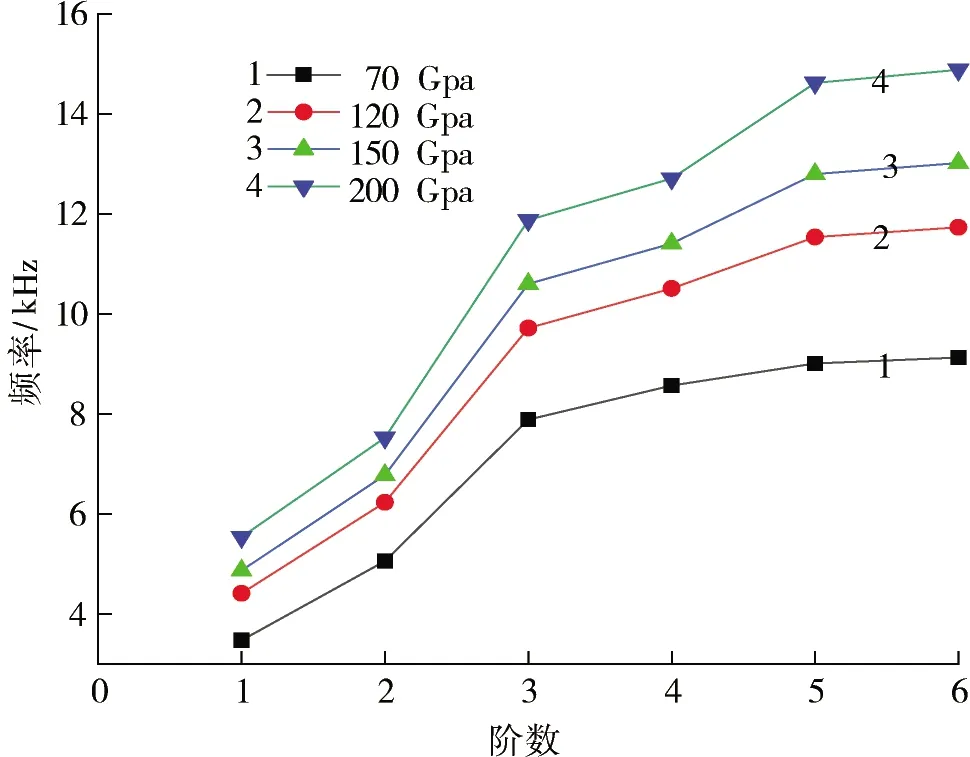
图8 弹性模量对定子固有频率的影响Fig.8 Effect of Young’s modulus of a stator on its natural frequency

图9 泊松比对定子模态频率的影响Fig.9 Effect of Poisson’s ratio on its modal frequency

4 结论

本文以一种小型直流电机为研究对象，分析了电机振动噪声的来源，借助于ANSYS的压电模块，用压电阻抗的方法，对小型直流电机的定子﹑转子进行了建模与仿真，得到了定子﹑转子的固有频率，确定了转子和定子在10 240，11 560和14 800 Hz 3个频率点附近的共振频带。通过仿真与压电阻抗实验结合的方法，找出了定子、转子的固有频率。模拟实验结果发现，定子的厚度、材料等参数能改变其固有频率、错开定子与转子的共振频带，避免电机共振，降低电机噪声。

1)定子的固有频率随着定子壳厚度的增加而增大，定子的固有频率随着弹性模量增加定子的模态频率也随之增大，材料的密度随着定子壳材料的密度增加而减小。

2)定子的固有频率不受泊松比的影响。

3)压电阻抗技术可以用于小型直流电机的降噪。