具一般指数函数核的Hilbert型积分不等式

刘琼

(邵阳学院 理学院，湖南 邵阳，422000)

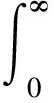
(1)

成立，右边的常数因子π是最佳值,式(1)称为Hilbert 积分不等式, 它在分析学和其他一些学科中有着重要应用[1-2]。100多年以来，Hilbert积分不等式的推广和加强，对新积分核的挖掘和创新以及积分核的参量化等研究一直是一个热门问题，特别是在近10年，对Hilbert型积分不等式的研究有了较大的发展，取得了诸多新的成果[3-9]。

(2)

刘琼等[11]引入参数α和β，将式(2)进行了推广：

(3)

本文利用基于“Hardy插值难题”的权函数方法和实分析中的一些技巧，对不等式(2)和式(3)进行再推广研究。 为此，引入多个参数构造新积分核K(x,y)：=e-αxμyν(α>0,μ,ν≠0)，对其进行参量化研究，得到了1个具有上面一般指数函数核的Hilbert型积分不等式和它的等价形式，它们的常数因子被证明是最佳值。应用上，考虑了不等式的算子范数表示式，并通过选取合适参数值，获得了一些特殊情形的Hilbert型积分不等式。

1 引理

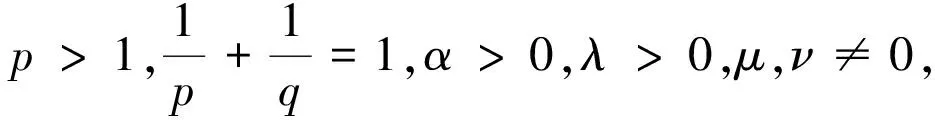
则有

(4)

证明令xμyν=t, 当ν>0时, 有

当ν<0时, 有

yq(1-λν)-1。

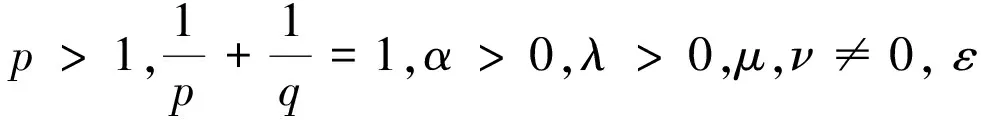
若常数μ和ν异号, 定义下面2个可测实函数:

则有

(5)

(6)

证明当常数μ和ν同号时，易得

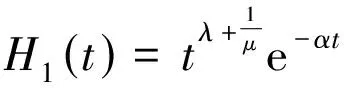
2)当μ<0,ν<0 时, 令xμyν=t, 注意到e-αt≤1(t≥0),有

当常数μ和ν异号时,容易得到

3)当μ>0,ν<0时,令xμyν=t,并注意到e-αt≤1(t≥0),得到

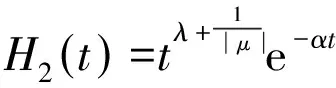
综合上面的讨论,可得式(5)和式(6)成立。

2 主要结果

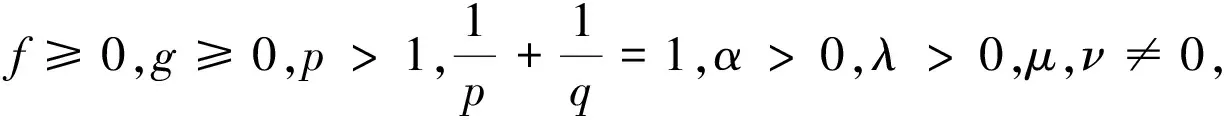
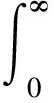
则下面不等式

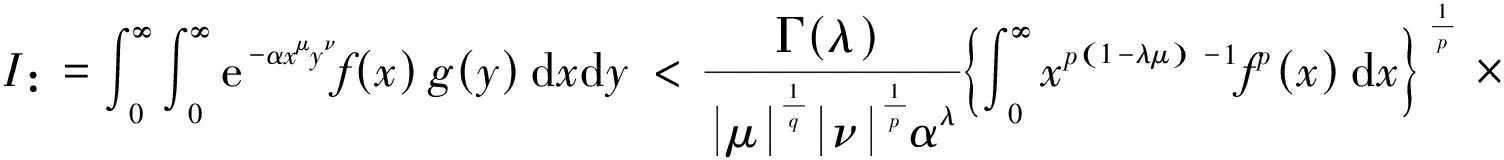
(7)

成立。

证明由带权 Hölder不等式[18]和引理1,有

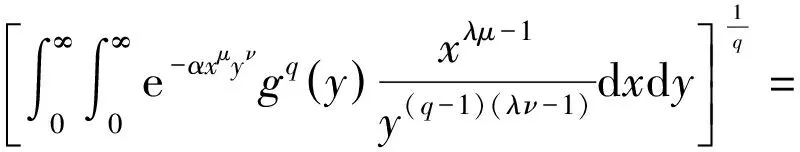
(8)

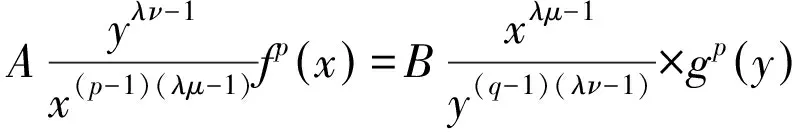
定理2 设有与定理1相同的条作,下列不等式

(9)

成立,且式(9)和式(7) 等价。

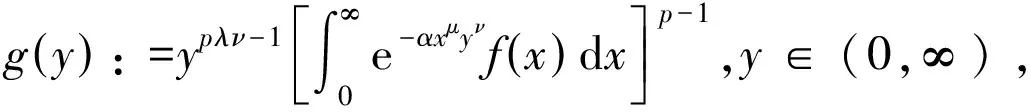
由定理1可得

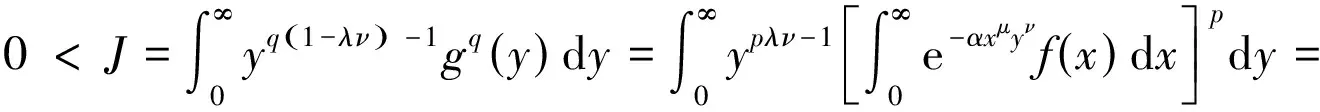
(10)

由式(10),得到

对上式两边取p次方，即得式(9)。

另一方面,由带权Hölder不等式、Fubini定理[19]和式(8),则有

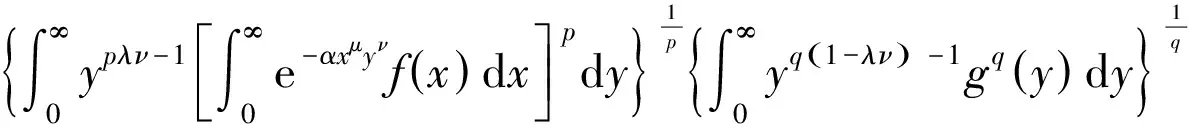
上式即为式(7)。所以，式(9)和式(7)等价。

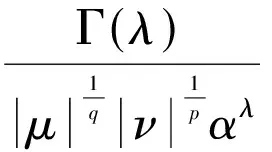
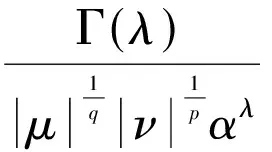
在定理1中条件成立的前提下,设置如下函数:

φ(x)：=xp(1-λμ)-1,ψ(y)：=yq(1-λν)-1,

显然有

ψ1-p(y)：=ypλν-1,(x>0,y>0)。

定义如下赋范线性空间:

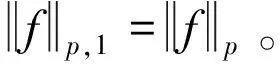
设f∈Lp,φ(R+),定义一个奇异希尔伯特型积分算子T:Lp,φ(R+)→Lp,ψ1-p(R+),

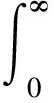
对于f∈Lp,φ(R+),g∈Lq,ψ(R+), 分别定义T和g的形式内积和T的算子范数如下：

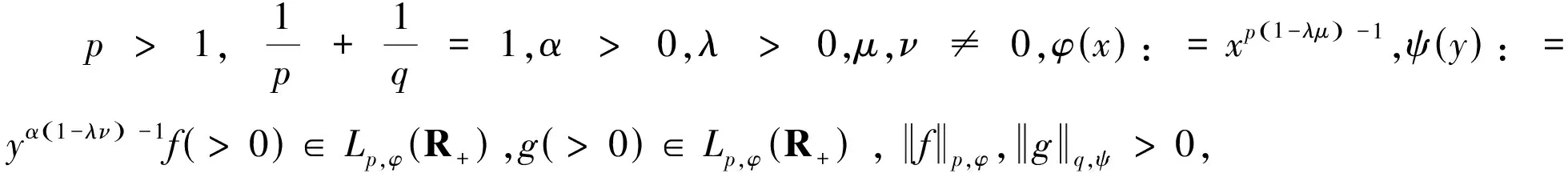
(11)

(12)

3 一些特殊情形的Hilbert型积分不等式

不等式(7)和式(9)包含所有具有指数核的Hilbert型积分不等式。 在应用上，可根据具体情况，通过选取合适的参数值，相应地得到所需要的估值不等式。 在此，示例一些形式简美的等价Hilbert型积分不等式。

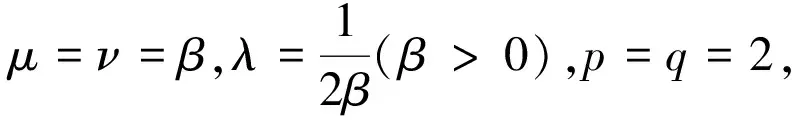
(13)

(14)

这里的常数因子π是最佳值。

例题2 取α=β=λ=1,p=q=2,得到参考文献[9]中出现的另一个等价不等式：

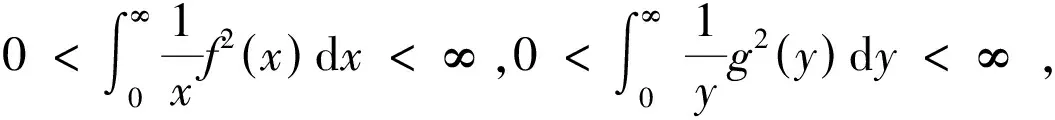
(15)

(16)

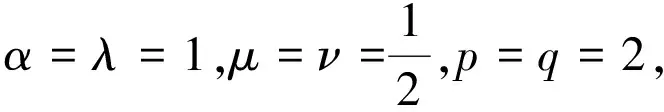
(17)

(18)

式(17)和式(18)右边的常数因子2和4均为最佳值。

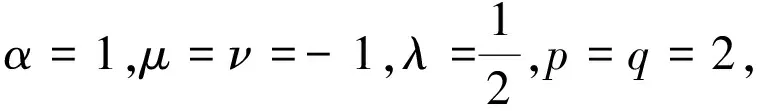
(19)

(20)

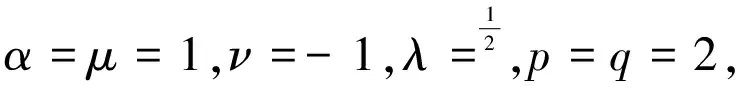
(21)

(22)

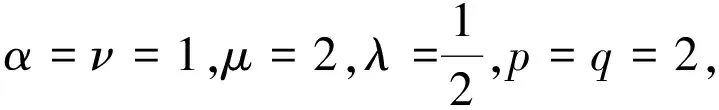
(23)

(24)