一种新型的风电输出功率分解方法

唐杰,姜有华,李智珍,邓琪伟

(邵阳学院 多电源地区电网运行与控制湖南省重点实验室，湖南 邵阳，422000)

随着风电渗透率的逐年增加，风电出力呈现出随机性、强波动性的特征，给电力系统的稳定运行带来了巨大的挑战，风电接入电网和风电消纳问题成为了限制风电大力发展的主要因素[1-2]。蓄电池与超级电容组成的混合储能系统具有双向充电特性，可为电力系统提供快速的响应能力，已经成为对风电输出波动功率平抑的有效手段之一。由于蓄电池与超级电容具有介质频率特性，导致蓄电池与超级电容只能吸收特定频段的风电功率，如果让其吸收特定频段以外的风电功率，会使蓄电池与超级电容的使用寿命和使用效率降低。因此，如何将风电波动功率分解为不同频段的功率，使得蓄电池与超级电容准确、快速地进行吸收风电功率是提高储能设备使用寿命和使用效率的关键[3-5]。

作为风电波动功率平抑的前提，风电输出功率的分解结果意义重大，其分解的精确程度与速度都决定了风电输出功率是否能够快速、准确地平抑。目前，主要的功率分解法有基于傅里叶变换法、经验模态分解法、集合经验模态分解法、小波与小波包分解法。基于傅里叶变换的分解方法能够对风电输出功率信号进行频谱分析，把信号分解成不同频段的信号，但是在分解过程中存在频谱泄露和栅栏现象等缺点，并且该种分解法无法进行时域分析，不能对非平稳的风电输出功率信号进行比较好的分解[6]。文献[7]采用经验模态分解法对风电输出功率进行分解，但是这种方法存在模态混叠问题和边界效应。集合经验模态分解法是在经验模态分解法的基础上进行了改进，但不能完全避免模态混叠现象[8]。文献[9-10]采用小波包方法对风电输出功率进行分解，但是小波包分解过程存在计算量巨大、耗时长等缺点，对风电输出功率分解的实时性有严重的影响。针对上述问题，寻找一种计算复杂性低、准确性高以及运行速度快的算法显得极其重要。

综合上述文献，为了能准确、快速地将风电输出功率进行有效分解，本文将小波变换与小波包变换的优势进行结合，既具有小波变换计算复杂性低、用时少的特点，又具有小波包变换算法对风电输出功率的高频部分的高分辨率的特点。利用该方法不仅提高了分解过程的快速性，还提高了分解结果的准确性。

1 风力发电系统组成及能量流动关系

风力发电系统结构图见图1，由风电场、蓄电池、超级电容、DC/DC与DC/AC变换器组成。风电场采用双馈异步发电机组，机组出力直接接入交流母线。超级电容与蓄电池组成的储能系统先经过DC/DC变换器与直流母线相连,再经过DC/AC变换器与交流母线相连。

图1中，PW(t)为风电原始输出功率；PGrid(t)为满足并网条件的并网功率；PHess(t)为平抑风电波动功率时储能系统吸收或者补偿的总功率；PSC(t)为超级电容吸收或者补偿的功率；Pb(t)为蓄电池吸收或者补偿的功率。

本文以某风电场的输出功率数据为研究对象，单机容量为40 MW，采样时间为10 s，总的采样时间为500 min，风电场的输出功率曲线见图2。

图1 风力发电系统结构图Fig.1 Architecture of wind power generation system

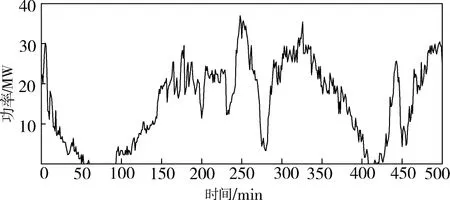
图2 风电输出功率曲线Fig.2 Wind power output trace

由图2可知，风电输出功率存在较大波动，若直接参与并网，会影响电力系统的安全稳定运行。因此，需要1种方法将风电输出功率中的波动功率提取出来，用混合储能系统吸收或者补偿，实现风电输出功率的平抑。

2 基于小波变换的风电输出功率分解

小波变换算法具有自适应变换-时频窗口的特点，可以精确地将信号分解为不同频段的信号。因此，小波变换除了能够对平稳信号进行准确的分解分析外，同时在对非平稳的风电输出功率信号的分解分析也有比较好的优势[11]。

设φ(t)=L2(R)为基本小波；φa,b(t)=L2(R)为连续小波。定义任意函数f(t)的小波函数解析式如式(1)所示。

(1)

式中：φ*(t)为φ(t)的共轭；a称为伸缩因子(又称尺度因子)；b称为平移因子。

利用小波变换对信号进行多层分解，得到1个低频信号和多个高频信号。以4层小波分解为例来说明小波变换的分解原理，小波变换的4层分解示意图见图3。

图3 小波变换四层分解示意图Fig.3 Four-layer decomposition diagram of wavelet transform

由图3可知，小波变换将原始信号分解得到1个低频成分和1个高频成分，再对上一次分解得到的低频部分再次分解。循环上述操作，直至最后的分解结果满足条件就停止分解。在上述分解过程中，小波变换每次分解时只对低频成分进行分解，忽略了高频部分的分解，使得高频部分的分辨率不高，不能将原始信号进行准确地分解。

本文采用db5小波对原始风电输出功率进行4层小波分解，仿真分析结果见图4，频率段的单位为10-3Hz。

图4 小波算法风电输出功率分解图Fig.4 Decomposition traces of wind power output by wavelet algorithm

由文献[12]可知，根据蓄电池的介质频率响应特性，确定蓄电池与超级电容的分界响应频率fn为16.7×10-3Hz。由图4可知，节点(4，0)为低频段功率，其余节点为各层的高频段功率。本文将满足并网条件的低频段功率直接并网，各层对应的高频段功率利用蓄电池与超级电容进行吸收或者补偿。考虑到蓄电池与超级电容的分界频率，在节点(3，1)处的高频段功率频宽太宽，不能准确地将该频段的功率分配给蓄电池与超级电容。

3 基于小波包变换的风电输出功率分解

由上述论证可知，小波变换在对风电输出功率进行分解时，只对低频成分进行分解，忽略了高频成分的分解，导致高频成分的分辨率过低，使得蓄电池与超级电容无法对高频部分的风电功率进行准确吸收或者补偿。小波包变换算法是1种使风电输出功率分解更加精细的算法，该算法不仅对低频成分进行分解，对高频部分进一步分解，能够得到频宽范围相对较低的高频部分，提高了高频部分的分辨率。小波包变换分解算法的解析式如式(2)所示。

(2)

式(2)中，hk和gk为低通滤波器和高通滤波器。采用小波包变换对风电输出功率进行分解时，小波包变换算法将风电输出功率信号进行均匀的划分，获得高分辨率、等频宽的低频信号和高频信号。以小波包的3层分解为例说明小波包的分解原理，小波包变换的3层分解结构示意图见图5。

由图5可知，利用小波包风电输出功率信号分解时，不仅对低频部分分解，而且对高频部分也进行无差别地分解，使得高频部分的分辨率比较高，但该分解过程计算量巨大、耗时长，影响了分解过程的实时性。

风电输出功率信号经过小波包变换，分解后得到了等频宽的低频信号和高频信号，其中每个信号频段的带宽为f0，计算公式如式(3)所示。

(3)

式中：fs为信号的采样频率；n为分解层数。

4 基于小波变换与小波包变换相结合的风电输出功率分解

针对小波变换与小波变换在对风电输出功率分解时存在准确性、实时性不足的问题，提出采用小波变换与小波包变换相结合的方法对风电输出功率进行分解。该方法首先采用小波变换对风电输出功率进行多层分解，得到满足并网条件的低频部分和多个高频部分。然后，针对蓄电池与超级电容都能吸收的高频成分进行小波包分解，提高高频部分的分辨率，使得蓄电池与超级电容能够准确吸收风电波动功率。小波变换与小波变换相结合的风电输出功率分解示意图见图6。

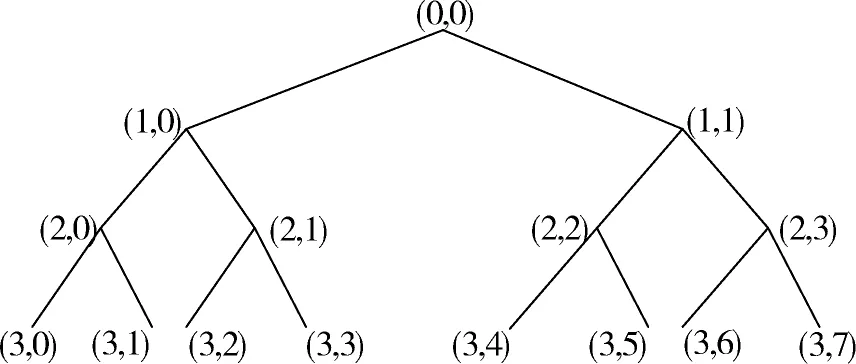
图5 小波包3层分解示意图Fig.5 Schematic diagram of three-layer decomposition of wavelet packet

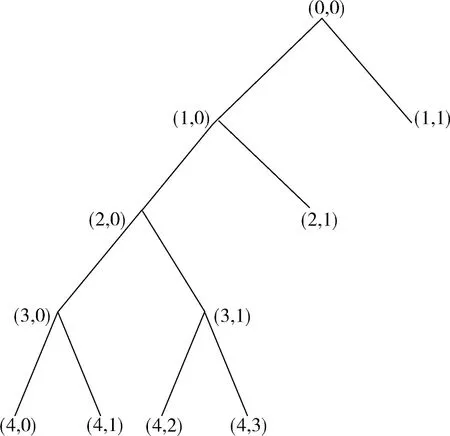
图6 小波与小波包变换相结合的分解示意图Fig.6 Decomposition diagram of combination of wavelet and wavelet packet transform

由图6可知：风电输出功率在经过小波分解后，再次利用小波包变换对某些需要分解的高频部分进行分解，提高了高频部分的分辨率。采用小波变换与小波包变换相结合的方法对风电输出功率分解的控制流程图见图7。利用小波变换对风电输出功率进行4层小波分解的结果见图4，然后，采用db5小波对蓄电池与超级电容都能吸收的高频功率进行1层小波包分解，提高该高频段功率的分辨率，使蓄电池与超级点能够准确吸收风电输出波动功率。该高频段功率小波包分解结果见图8。频率段的单位为10-3Hz。

图7 基于小波变换与小波包变换相结合的风电输出功率分解的控制流程图Fig.7 Control flow chart of wind power output power decomposition based on the combination of wavelet transform and wavelet packet transform

图8 特定频段风电功率小波包分解图Fig.8 Wavelet packet decomposition trace of wind power in a specific frequency band

风电输出功率经过小波变换与小波包变换分解后，得到了满足并网条件的低频功率P(4,0)(t)与蓄电池和超级电容的充放电功率Pb(t)与PSC(t)。Pb(t)与PSC(t)的计算公式如下所示：

PSC(t)=P(1,1)(t)+P(2,1)(t)+P(4,3)(t)

(4)

Pb(t)=P(4,1)(t)+P(4,2)(t)

(5)

由式(4)和式(5)计算得到蓄电池与超级电容的充放电功率，分别见图9和图10。

4.1 与小波变换进行准确性对比

考虑到蓄电池的循环寿命问题，若使其吸收或补偿较高频段的风电输出波动功率，则会使得蓄电池的充放次数增加，缩短其使用寿命。因此，需将经小波变换分解后得到的特定高频功率进行小波包分解，提高蓄电池与超级电容都能吸收的高频段功率的分辨率，使蓄电池和超级电容吸收各自响应频率范围内的风电波动功率。本文所提方法与传统小波变换方法都是将风电输出功率分解后，分别得到蓄电池的充放电功率。2种方法的蓄电池充放电次数对比见表1。

图9 蓄电池充放电功率Fig.9 Charge-discharge power trace of battery

图10 超级电容充放电功率Fig.10 Charge-discharge power trace of super capacitor

由表1可知：小波变换与小波包变换相结合的方法将风电输出功率分解后，蓄电池在吸收或补偿风电输出波动功率时的充放电次数与传统小波变换方法相比减少了约25%，有效提高了蓄电池的使用寿命。

表1 蓄电池的充放电次数Table 1 Charge and discharge times of battery

4.2 与小波包变换进行快速性对比

为验证小波变换与小波包变换相结合的方法在快速性上比传统小波包变换有所提高，通过仿真对小波变换与小波包变换相结合的方法分解风电输出功率的快速性进行验证。在相同的仿真参数和仿真环境下，采用小波包变换和小波变换与小波包变换相结合的方法对同一个风电输出功率信号进行分解并且重构，然后对2种算法各自的运行时间进行统计。将小波变换与小波包变换相结合的方法对风电输出功率进行10次分解重构，并将2种算法各自的运算时间与平均时间进行统计，统计情况见表2。

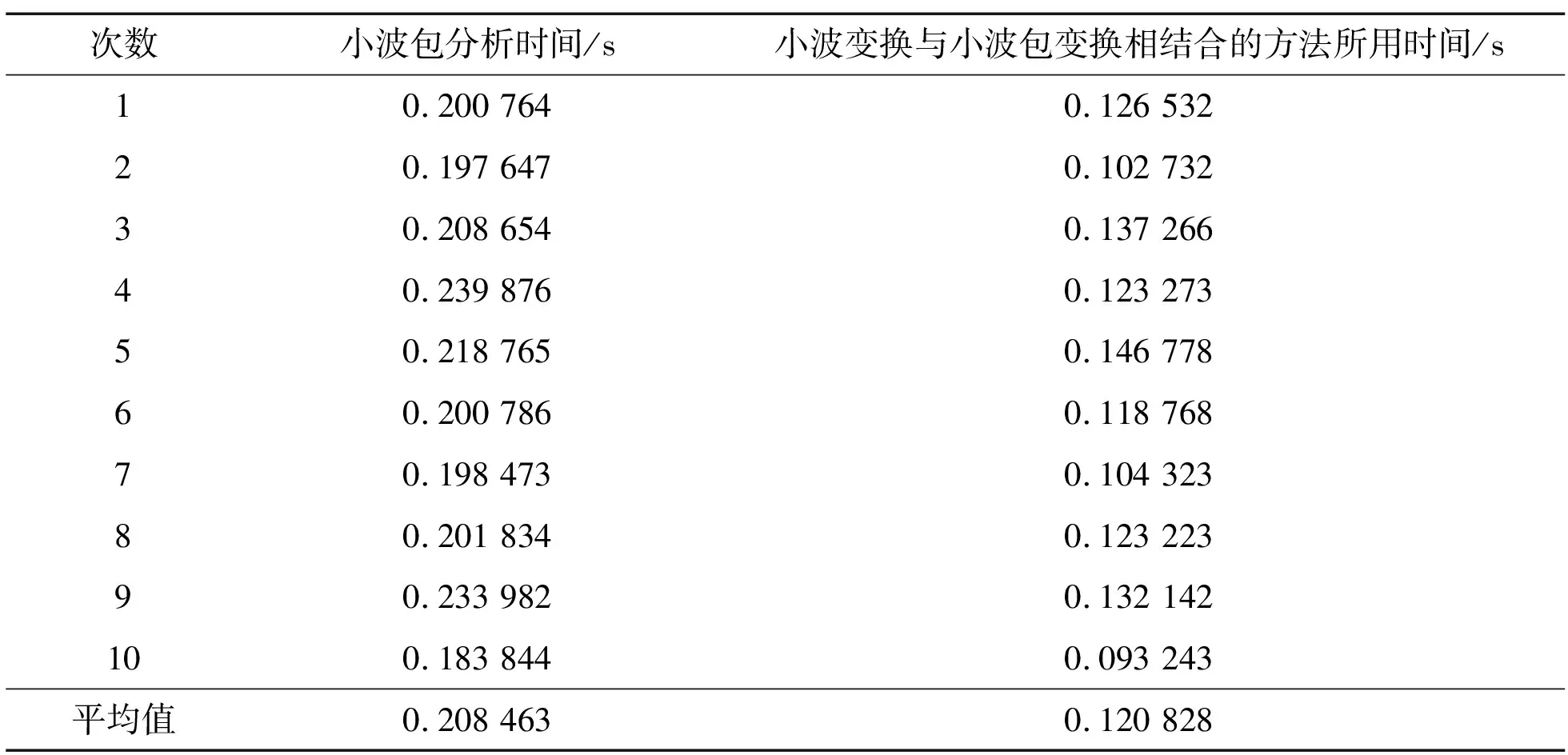
表2 2种算法的运算时间Table 2 Operation time of two algorithms

通过表2可以看出，利用小波包变换对风电输出功率信号进行分解重构的运算时间都超过了小波变换与小波包变换相结合的方法对风电输出功率信号进行分解重构的运算时间。利用小波包变换算法进行10次运算的平均时间为0.208 463 s，而小波变换与小波包变换相结合的方法进行10次运算的平均时间为0.120 828 s，比小波包变换用时快了大约42%。验证了小波变换与小波包变换相结合的方法对风电输出功率分解的时间减少，提高了分解过程的实时性。

5 结论

本文将小波变换和小波包变换的优势进行结合对风电输出功率进行分解，该方法不仅提高了对风电输出功率高频段的分辨率，还提高了风电输出功率的快速性。仿真结果表明，此方法能够有效地将风电输出功率的低频段和高频段分解开，与传统小波变换的分解方法相比，提高了高频段的分辨率，与小波包变换的分解方法相比，提高了分解过程的快速性。因此，小波变换与小波包变换相结合的分解方法在分解的准确性和快速性上要优于只用小波变换或者只用小波包变换。