基于GeoGebra设计与实现椭圆可视化动态课件

随着现代信息技术对数学教学支撑能力的增强，教师的教学活动不再局限于用静态的板书进行演示，用自然语言、符号语言解释数学概念，也不再局限于用幻灯片演示，而是可以动态可视化展示，使课堂更有趣味性与探究性。在这种情境下学习，学生掌握知识更加牢固。数字化教学还能激发学生的求知欲以及探索、实践的积极性。除了大众所熟知的几何画板、超级画板外，GeoGebra等数学绘图软件也被快速推广应用，这些工具的适当使用有利于提高教学效率。

一、GeoGebra在几何教学中的独特优势

目前，多数教师执教椭圆这一教学内容时还是利用PPT进行新课的讲授。用PPT制作的课件，在动态性、实时操作性上有一定的缺陷，不能实现信息技术与课堂的整合。例如，教师只能借助其他平台制作动画，再将动画录制成视频引入PPT中播放，无法实现动画应有的交互性。有些画板软件囿于版权以及对理论知识要求高等原因，用起来比较烦琐。GeoGebra软件具有开源、可视化程度高、简单易学等特点，逐渐获得教师认可。在人教A版高中数学选择性必修第一册教材中，运用的软件正是GeoGebra。GeoGebra是什么？这个单词由Geo和Gebra组成，也就是geometry（几何）和algebra（代数）。顾名思义，它是一款结合几何、代数甚至微积分的动态数学软件。GeoGebra在绘制动态图以及教学演示方面有其独特优势，可以作为可视化教学的工具。

笔者以椭圆为例，借助GeoGebra软件，探究动态课件的设计与实现方法，建立可视化与抽象的联系，以期突破“意会”与“言传”的障碍，实现高中数学课堂可视化教学，提升学生直观想象等数学核心素养。

二、椭圆动态课件的设计

（一）设计目标

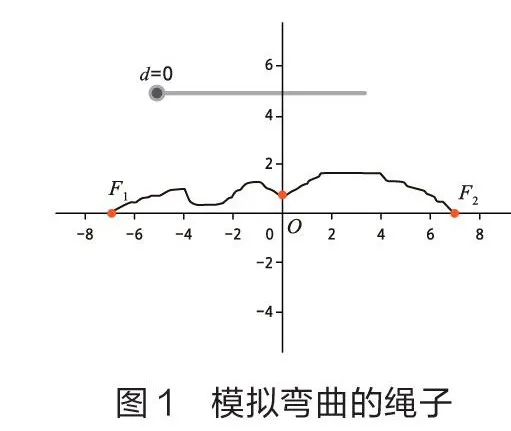
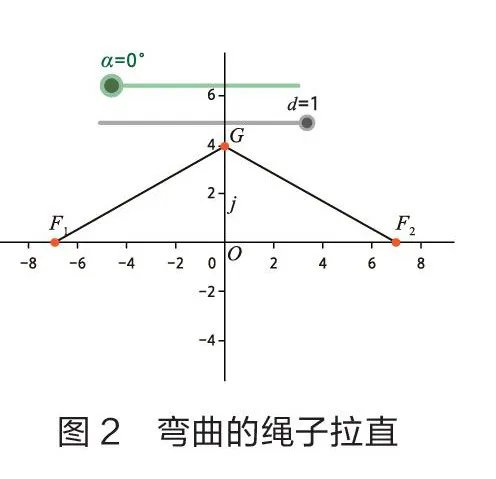
首先，借助GeoGebra实现人教A版高中数学选择性必修第一册第105页中的探究，即通过GeoGebra软件将两端被固定的一条弯曲绳子拉直。在弯曲的绳子上取一点，将绳子拉直后，移动这一点，绘制点的轨迹。通过这一动态过程展示椭圆的形成过程。

其次，利用GeoGebra的相关功能动态呈现椭圆的一些基本性质，如、的范围、对称性、顶点、离心率等。课堂上，通过GeoGebra实现动态的演示，引导学生思考，做出猜想，最后借助GeoGebra软件进行论证。

在这过程中，教师应用GeoGebra表格记录功能以及跟踪功能，开展探究性教学，引导学生思考参数、、是如何影响椭圆的扁平程度的，进而引出离心率概念，并探究离心率数值的大小如何影响椭圆扁平程度。

（二）难点突破

需要处理的问题：如何实现任意曲线的绘制;如何实现曲线拉直这一过程;曲线拉直后如何绘制椭圆的轨迹。

制作过程中需要用到一些指令，如曲线、轨迹、位似、如果等，以及一些工具，如画笔、折线、滑动条、复选框等，运用这些指令来解决问题，这是需要突破的难点。

1.曲线的绘制 ：使用GeoGebra的画笔工具，自由绘制想要的曲线，模拟绳子。

2.曲线拉直的实现：使用折线工具，绘制椭圆焦点与椭圆上一点的折线，在曲线上取一点，过该点作轴的垂线与折线的交点;建立滑动条，利用位似指令实现曲线拉直的动画过程，并通过滑动条实现这一过程的实时控制。

3.椭圆轨迹的绘制：利用曲线指令以及滑动条实现简单的动态绘制，再利用一些脚本指令，如启动动画、赋值等，优化动画的展示过程。

三、椭圆动态课件的GeoGebra实现

（一）实现椭圆形成的动态过程

人教A版高中数学选择性必修第一册教材对椭圆的定义是这样的：将平面内与两个定点、的距离的和等于常数（大于丨丨）的点的轨迹叫作椭圆（ellipse）。在教学过程中，学生很难进行直观想象;囿于常规教具，也很难实现这一动态作图过程。教师借助GeoGebra软件，制作动画来演示这一过程，让学生对椭圆的第一定义有更加直观的认识。

绘图目标：弯曲的绳子两端被固定，在绳子上的取一点，将绳子拉直，拉之后进行椭圆的动态绘制。

绘制步骤如下：

1.利用滑动条工具，建立滑动条、，其区间分别设置为（0，10）和（0，），增量均为1。

2.在输入框中输入 ：^2/^2+^2/^2= 1，得到椭圆方程。

3.在输入框中输入：_1=焦点（），得到焦点和。

4.在输入框中输入：顶点（），得到椭圆的4个顶点分别为、、、。

5.用画笔工具，以为起点，为终点，描一段弯曲的绳子，得到stroke1。

6.用折线工具，依次连接、、、，得到折线。

7.利用描点工具，在stroke1上描点，得到点。

8.在输入框中输入：交点（垂线（， 轴）， ），得到点。

9.利用滑动条工具，建立滑动条，其区间设置为（0，1），增量默认不填，动画设置为“递增（一次）”。

10.在输入框中输入：位似（， ， ），得到点。

11.在输入框中输入：轨迹（， ），得到轨迹loc1。

12.利用复选框工具，命名为隐藏辅助线，在绘图区中分别点击笔触stroke1、点、折线。

13.利用滑动条工具，建立角度滑动条，将其区间设置为（0°，360°），增量为1°;将动画一栏速度设置为3，递增（一次）。

14.在输入框中输入：曲线（cos（），sin（），，90°，90°+），得到参数曲线。

15.在输入框中输入：（ + 90°），得到点。

16.利用复选框工具，以标题为顶点，在代数区单击顶点、、、，实现通过复选框控制顶点的出现。

17.右击滑动条，选择属性，在脚本更新中输入“启动动画[，==1]”。

18.右击滑动条，选择属性，高级显示条件中输入：==1。脚本中更新时输入：如果（ == 0，赋值[，0°]）。

19. 利用折线工具，依次连接点、、、，得到折线。

20.按住Ctrl键，在代数区单击点、折线，右键属性，在高级显示条件中输入：=1。

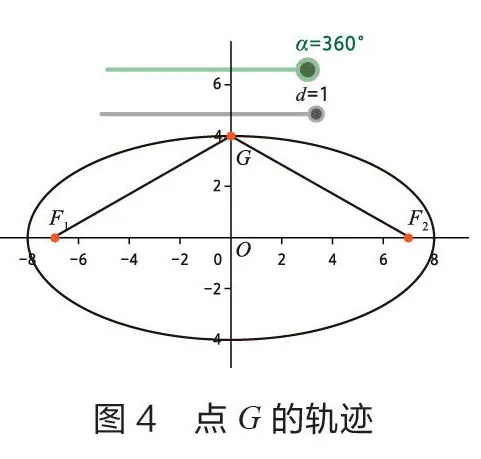
按以上步骤，绘图完毕。此时可以通过控制滑动条，实现椭圆的动态绘制过程。当=0，是一条弯曲的“绳子”，的值从0到1的过程中，是实现“绳子”被拉直的过程。当=1时滑动条就会自动启动，实现模拟椭圆的绘制过程（如图1至图4）。

（二）实现椭圆的简单几何性质的动态演示

教学中，大部分教师使用PPT讲授椭圆的简单几何性质时会参考一个表格（见表1）进行动态课件的展示。但是这样操作无法让学生获得直观的感受。GeoGebra的应用为解决这一问题提供了便利，它不仅支持PPT中的动画功能，而且可以支持教师控制参数实现动画变化，使抽象的知识变得直观，利于学生更好地理解和记忆。

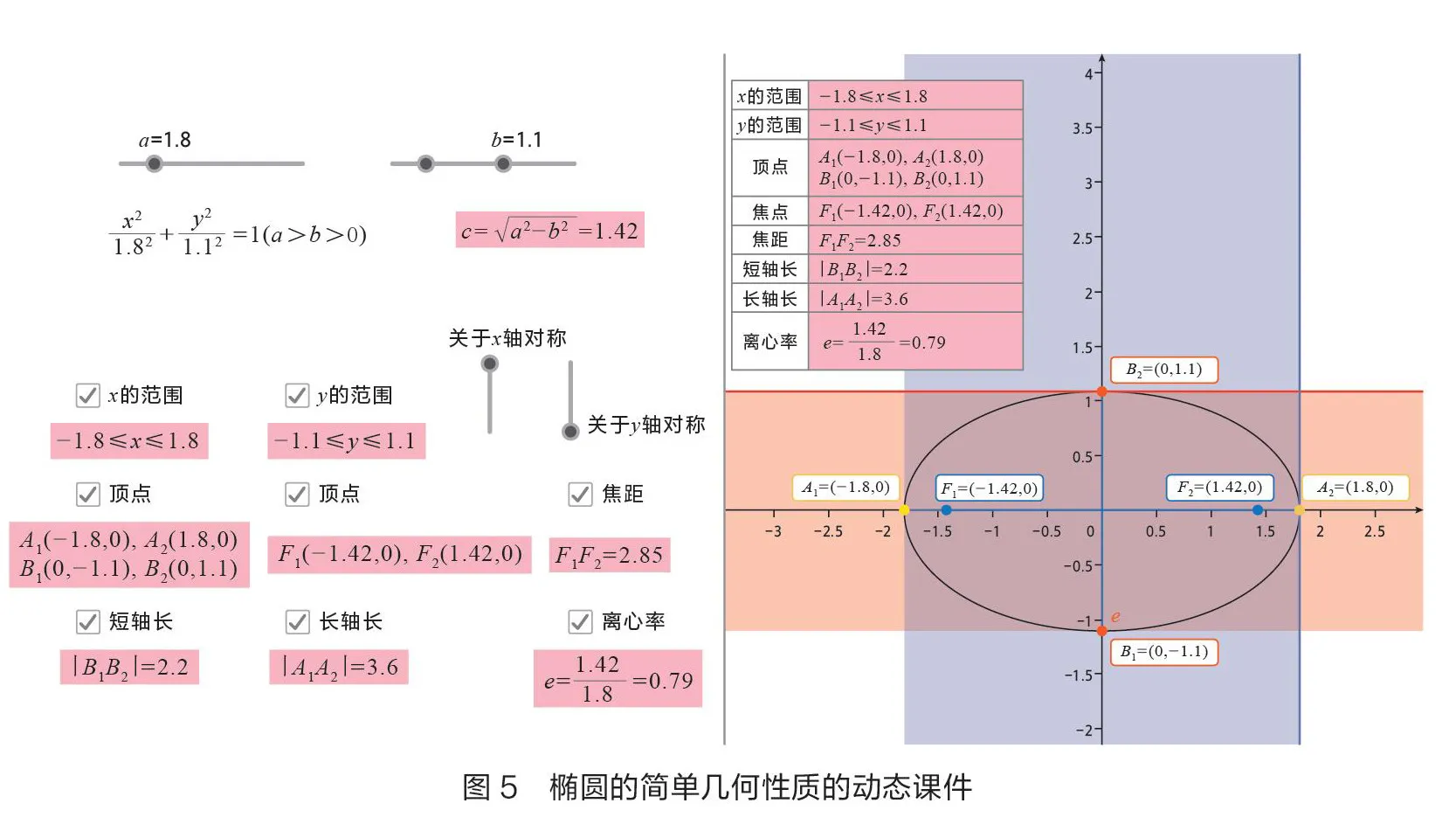
表2呈现的是椭圆的简单几何性质动态课件的实现结果。教师在GeoGebra 软件的输入框中输入表2定义栏中的内容后，通过复选框工具、文本工具以及表格文本指令，可以实现几何性质的动态演示。教师通过控制滑动条、改变椭圆的各个参数，从而改变椭圆的形状;使用复选框工具，可实时控制每个基本性质的显示与隐藏。最后，所有的基本性质被汇总在一个表格里系统地呈现。

动态课件的整体展示如图5所示，左侧是控制区，也是数值显示区，右侧则是图象显示区与表格汇总区域。除了可以通过复选框控制基本性质的展示外，教师还可以通过名为“关于轴对称”“关于轴对称”的两个滑动条，控制关于椭圆对称性的动画演示。

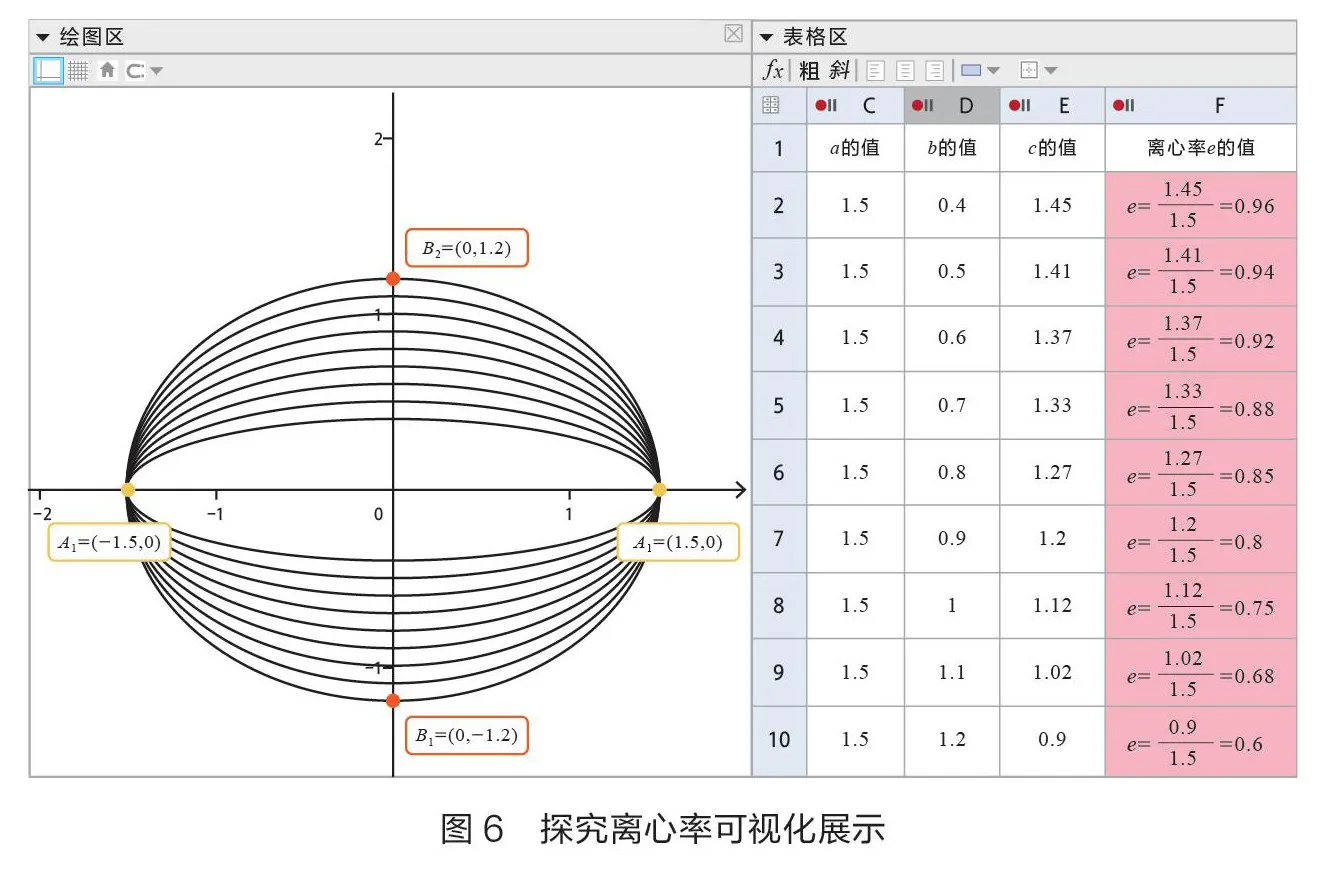
教师还可以利用GeoGebra的“显示跟踪”功能，通过改变、的值，对椭圆的轨迹进行跟踪;同时引导学生思考椭圆的扁平程度与参数、、之间的关系。教师借此引出离心率，让学生结合刚刚的动画演示教学，总结离心率与椭圆的扁平程度规律。

教师可以控制滑动条，利用GeoGebra自动记录数值的功能以及“跟踪功能”，实现数形结合的可视化展示（如图6）。随着值逐渐增大，离心率变小，椭圆就越圆。这有助于学生证明其猜想或推论正确与否。

在高中数学的教学中，用GeoGebra软件制作可视化动态课件有着广阔的天地。教师科学应用信息工具可实现抽象概念可视化，解题可视化，教学可视化。利用可视化的动态课件可以创设情境，让学生记录、观察，条件允许的情况下还可以让学生动手操作。软件演示可为学生猜想、证明提供一定的帮助。教师在此基础上引导学生进行论证，得出结论，这样效果更好。基于GeoGebra制作的动态课件可用于可视化教学，引导学生思考。可视化交互有利于学生交流思想，主动构建知识网络结构，引发其探究、论证。学生经历解决问题的全过程，对知识的学习会更加扎实，成效会更显著。

（作者系广东省广州市亚加达外国语高级中学教师）

责任编辑：祝元志