基于矢量误差修正的实时负载牵引测量模型方法

王一帮,栾 鹏,霍 晔,吴爱华,梁法国,杜 静

(1.中国电子科技集团公司 第十三研究所,河北 石家庄 050051；2. 陆军步兵学院,河北 石家庄 050051)

1 引 言

在无线通信、雷达、电子对抗中体积小、耗电少的微波功率放大器需求增长迅速,单片微波集成电路(MMIC) 由于其工作频带宽、增益高, 获得了广泛的应用。微波功率晶体管作为功率MMIC 芯片的核心部分, 其性能好坏对MMIC的性能起着至关重要的作用, 所以对微波功率晶体管的设计进行优化有着重要意义。

负载牵引测量系统在功率晶体管的设计过程中起到了重要作用,大大提高了设计效率[1～8]。但传统负载牵引测量系统由于其测量模型的原因,即需要在自校准过程中用矢量网络分析仪对各频点处的源、负载阻抗状态进行预表征,然后存入软件内部,待实际测试过程中再将阻抗调配器配置到相同的阻抗状态下(通过调节调配器内部机械探针实现),并将已存数据调出来,结合功率计示值测得绝对功率[9～12]。因此,阻抗调配器的机械重复性对测试精度影响很大。在低频段26.5 GHz以下,阻抗调配器的重复性可以得到保证,随着频率进入8 mm及以上频段,阻抗调配器的重复性变得较差。另一方面,负载牵引测量系统中需要大量的S参数计算,以将测量参考面计算到被测件的输入输出端口,进而求得被测件功率、效率、增益等。大量的S参数计算将导致测量的误差积累,同样影响测试准确度。

近年来,不依赖于阻抗调配器重复性的实时负载牵引测量系统得到了广泛应用。它通过对矢量网络分析仪(后面简称矢网)的矢量误差修正和一次绝对功率校准,就能采用矢网内部接收机进行绝对功率测量,有效降低了测试重复性。矢网内部接收机具有更高的线性度,因此,它也具有更高的动态范围。科学家们对实时负载牵引系统准确度的提升也做了很多研究[13]。但迄今为止,尚未见文献详细讨论测量模型并给出计算公式。本文将从最基本的误差模型开始,给出测量模型的求解过程。然后搭建相应的硬件系统,并进行准确度的验证,最后给出结论。

2 测量模型的建立

2.1 负载牵引测试理论基础

负载牵引测量系统的目的是测量被测件在不同源阻抗、不同负载阻抗下的功率输出、增益、效率等参数,并在史密斯圆图上画出相应的等值圆图,设计工程师根据具体设计目标折中选取最佳设计参数。图1是基于矢量修正的实时负载牵引测量模型示意图,其中：a1,b1为端口1处输入输出电压波；a2,b2为端口2处输入输出电压波；Γin为输入反射系数；Pin为被测件输入功率；ΓL为被测件输出端负载反射系数；PL为被测件输出功率,也称为负载吸收的功率。功率增益GOP为输出功率PL与输入功率Pin的比值。参数定义如式(1)～式(5)所示。被测件效率和附加效率可以结合容易获得的直流功率计算得到。

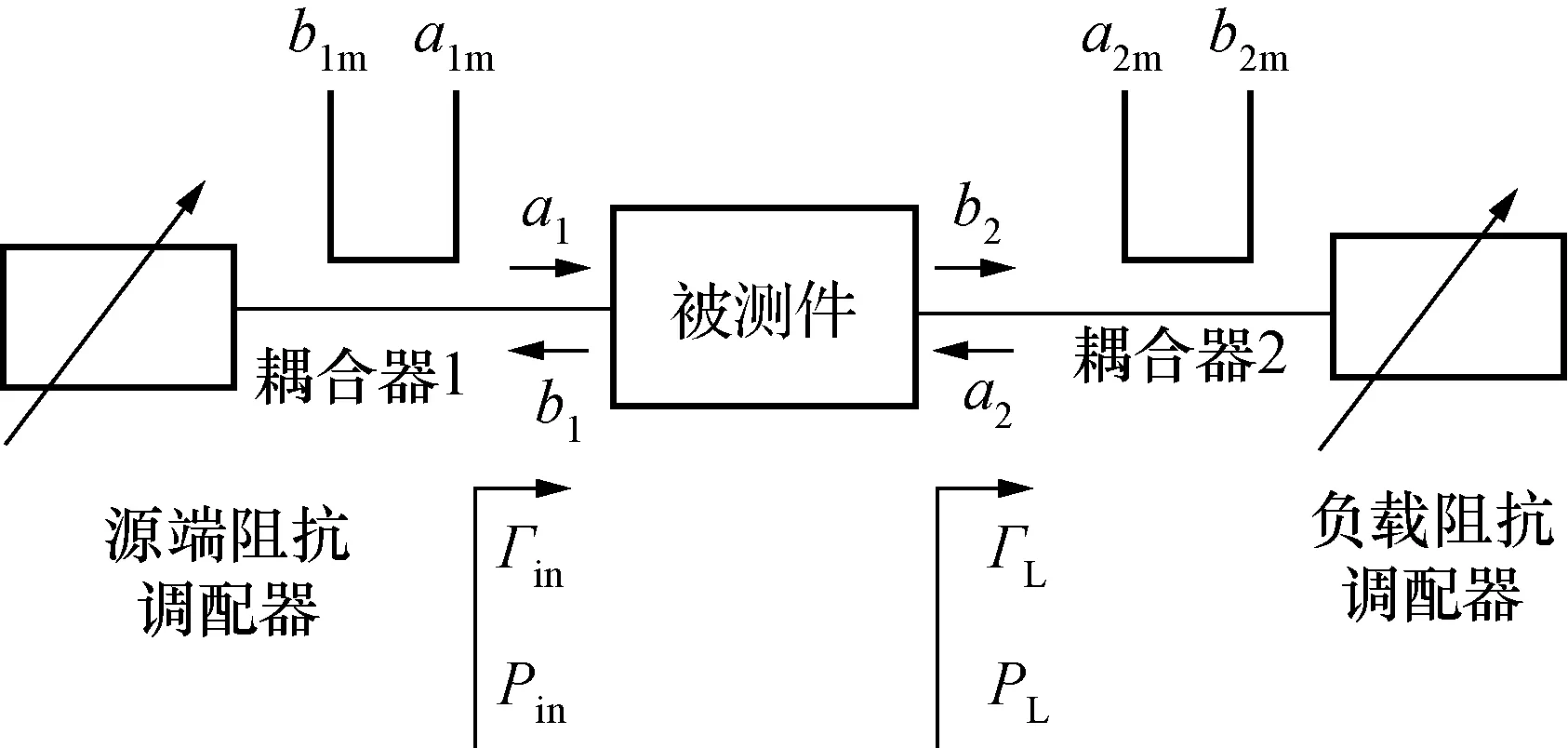
图1 基于矢量修正的实时负载牵引测量模型示意图Fig.1 Schematic diagram about real-time load pull system based on vector correction

Γin=b1/a1

(1)

ΓL=a2/b2

(2)

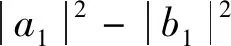
(3)

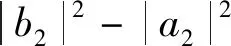
(4)

GOP=PL/Pin

(5)

基于矢量修正的实时负载牵引测量模型原理图如图1所示。被测件输入输出端分别连接双定向耦合器,双定向耦合器外端再连接阻抗调配器。双定向耦合器耦合端连接矢网内部接收机或功率计,用来对被测件任意源阻抗和负载阻抗条件下的电压波进行实时监控。考虑到在测试过程中,被测件的源阻抗和负载阻抗不断变化,若采用12-term误差模型,其负载匹配、传输跟踪将随着源阻抗和负载阻抗改变。因此采用矢量修正的8-term误差模型[14],它是整个负载牵引测量系统模型的基础。8-term误差模型信号流图如图2所示。8-term误差模型实际独立量只有7个,分别为e00,e10e01,e11,e22,e23e32,e33和e10e32。8-term 误差模型可通过TRL、多线TRL[15,16]或LRRM校准直接求得,也可通过SOLT校准计算得到12-term误差,再计算得到。

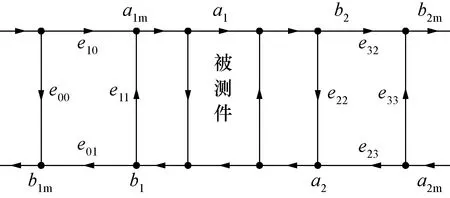
图2 8-term误差模型Fig.2 8-term error model signal flow

信号流图能清晰表明输入输出电压波与功率波信号的关系,其中包括所有将要预估的误差项。输入端口和输出端口的信号流图分别见图3和图4。

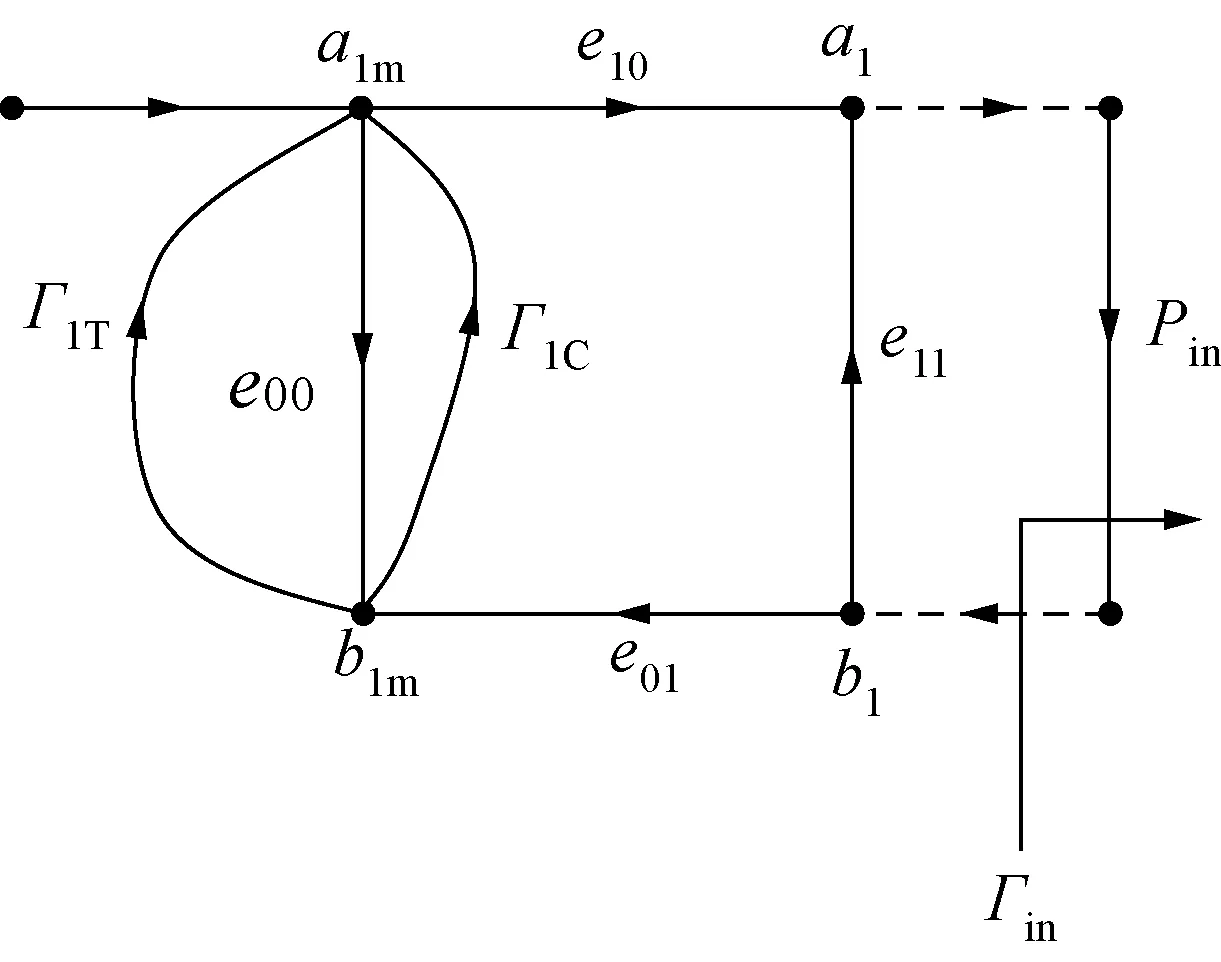
图3 输入端口测量模型Fig.3 Signal flow error model of input port

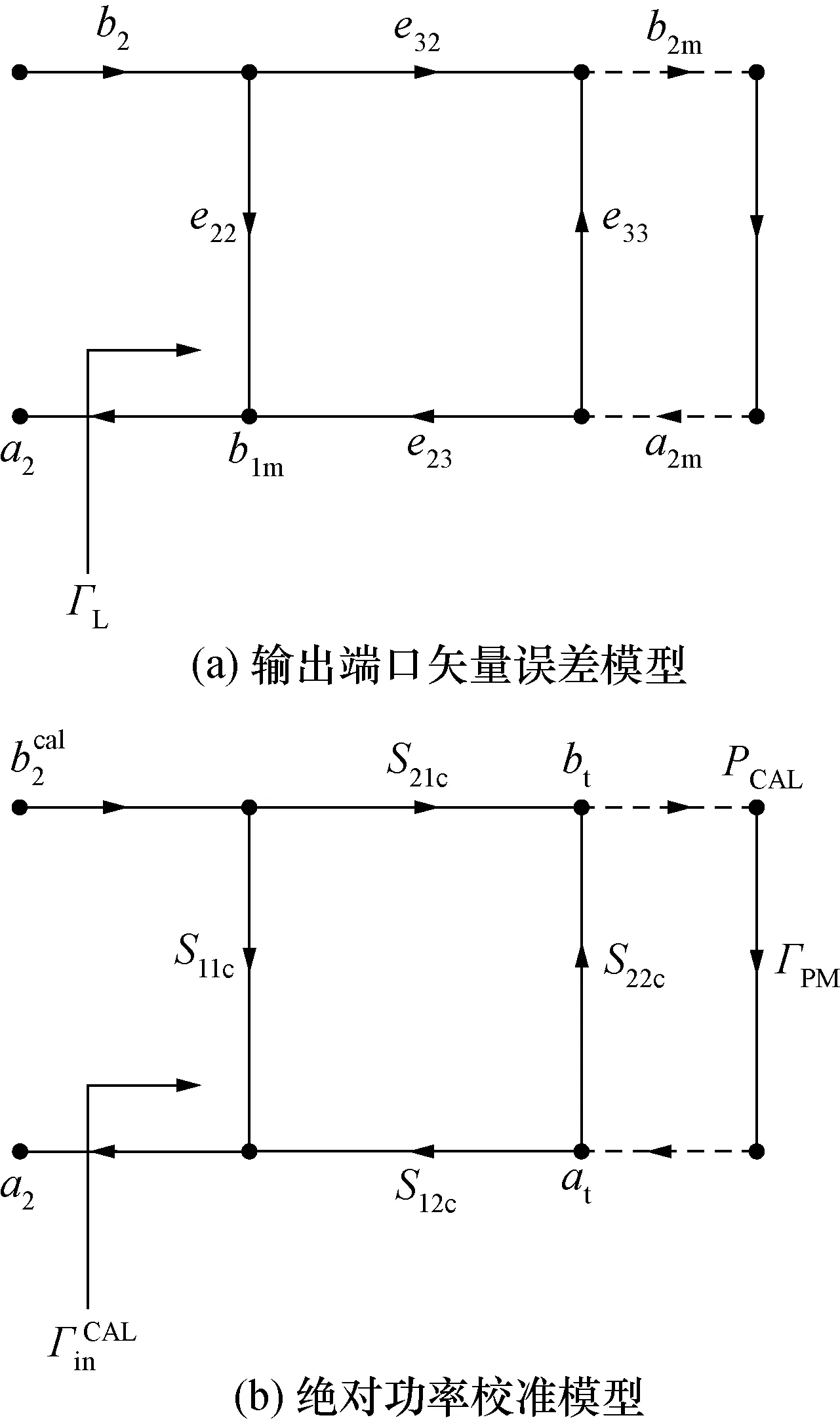
图4 输出端口测量模型Fig.4 Measurement model for output port

2.2 输入端口测量模型

图3为输入端口测量模型,e00,e10,e01,e11为端口1处4个系统误差项,a1m,b1m为耦合器1实时测试输入电压波和输出电压波,a1,b1为被测件端面实时的输入电压波和输出电压波,Γ1T为源端阻抗调配器对双定向耦合器输入端产生的影响,Γ1C为双定向耦合器耦合度有限产生的影响。Γin为连接上被测件DUT后,被测件输入反射系数。Pin为流入被测件的功率。

放置DUT后：

(6)

可推导出：

(7)

当接被测件,由图3所示信号流图可知：

a1me10+b1e11=a1

(8)

(9)

(10)

式(10)即为基于矢量误差修正技术得到的负载牵引测量系统输入端口Pin的测量模型。

2.3 输出端口测量模型

图4为输出端口测量模型,包含输出端口矢量误差模型和绝对功率校准模型。图4(a)中e22,e23,e32,e33为端口2处4项系统误差项,a2m,b2m为耦合器2实时测得的电压波。a2,b2为被测件输出端输出电压波和输入电压波。ΓL为被测件负载反射系数。类似上节,被测件负载反射系数ΓL可推得：

(11)

式中：

(12)

同样,由图3(a)信流图可知：

b2m=e33a2m+e32b2

(13)

得：

(14)

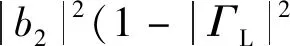
(15)

2.4 功率校准求得e10,e32模的平方

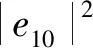
(16)

(17)

可得：

(18)

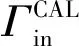
(19)

图4(b)所示为绝对功率校准信流图。ΓPM表示功率头的反射系数,PCAL表示功率计进行校准时的功率示值,Sijc表示被测件输出端面和负载端阻抗调配器输出端的两端口散射参数。经过推导可得：

(20)

|e32|2可通过式(21)求解：

(21)

根据功率增益公式,最终求得：

(22)

式(7)、式(10)、式(11)、式(15)和式(22)为本文推导出的基于矢量误差修正技术得到的负载牵引测量系统最终的测量模型。

3 准确度验证

根据实时测量模型建立的负载牵引测量系统如图5所示(同轴测量系统的话,去掉探针部分即可)。系统包括微波信号源(源端信号源和负载端信号源使用矢量网络分析仪内部信号源)、隔离器、源端/负载端功率放大器(选配)、源端/负载端阻抗调配器iTuner-5080、双定向耦合器、功率计E4419B、矢量网络分析仪N5244A和探针测量系统等组成。源端/负载端双定向耦合器经衰减器与矢网内部接收机相连。图中：a1,b1为被测件输入端电压波；a2,b2为被测件输出端电压波；am1,bm1,am2,bm2为矢网内部接收机测得电压波；Γin为被测件输入反射系数；ΓL为被测件负载反射系数。PCAL为功率计测得负载阻抗调配器输出端,用于绝对功率校准。系统测试范围26.5～40 GHz,校准样片为Cascade公司101-190C。

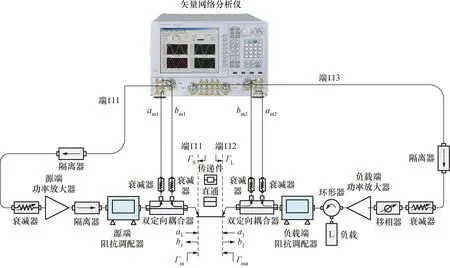
图5 实时负载牵引测量系统示意图Fig.5 Schematic diagram of real-time load pull measurement system

端口1和2的输入反射系数Γin和输出反射系数ΓL,其测试模型与矢网的误差模型本质上是一致的,因此其准确度自然得到保证。

采用测量模型对直通传输线的功率增益进行了测量,在负载反射系数分别为0.2～0.9,相位为10°情况下进行了测量,26.5 GHz功率增益GOP测量结果如表1所示。

表1中随着负载反射系数模值增加,实时模型测得的功率增益GOP逐渐偏离理论值,这是由于校准的剩余误差造成的,剩余误差来源于矢量网络分析仪校准的不完善、测试重复性、仪器偏移等因素。

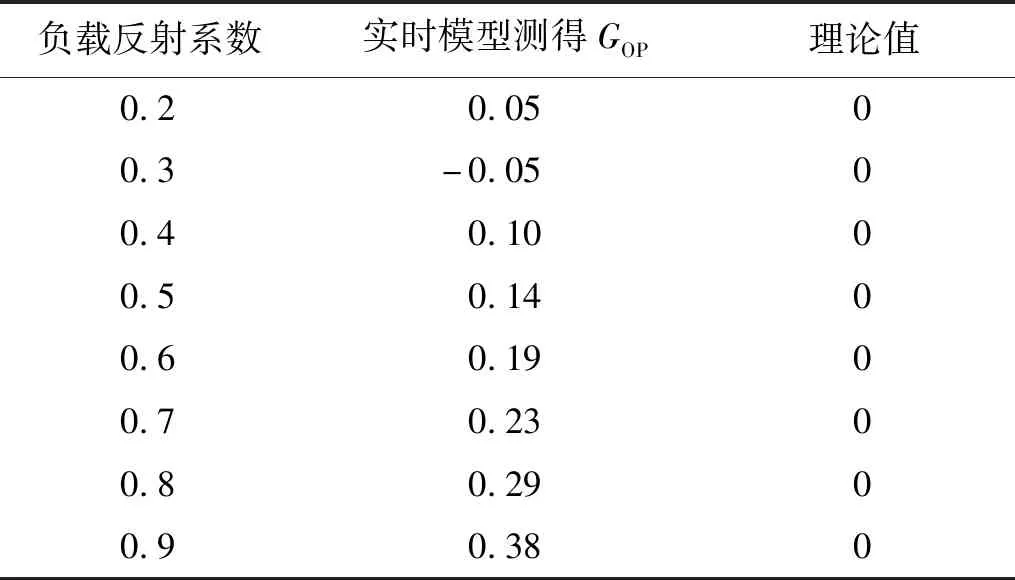
表1 GOP测量结果Tab.1 Measurement results for GOP dB

本文测量模型与商用的Focus实时负载测量系统进行了比较。比较方案为双方测量模型输入的原始数据完全一致,比较输出结果差异。实验表明,两者输入反射系数和负载反射系数完全一致,这一点符合文中的理论分析。输入功率Pin最大相差0.10 dB以内,输出功率Pout相差0.20 dB以内,GOP相差0.30 dB以内,部分结果见表2。

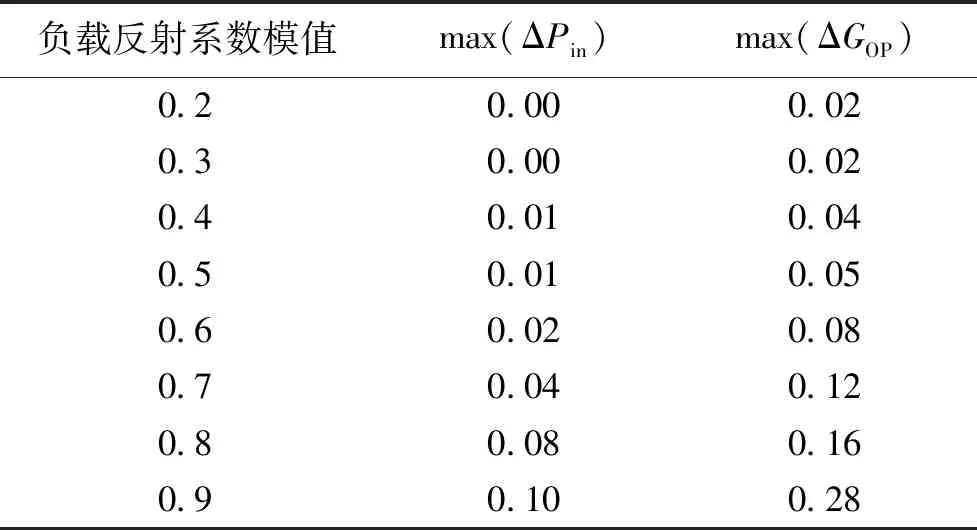
表2 与商用系统对比测量结果Tab.2 Measurement results comparison with commercial system dB

4 结 论

提出了一种新型的基于矢量误差修正的负载牵引测量模型方法,从8-term矢量误差模型入手,建立接收机与被测件端口处电压波的函数关系。相比于传统的负载牵引测量系统模型,避免了阻抗调配器重复移动带来的系统误差,同时采用矢量网络分析仪内部接收机测量绝对功率,也提高了系统测试的动态范围。根据测量模型搭建了实时负载牵引测量系统,测量结果与商用系统的测试进行了对比,实验表明该模型具有相当的准确度。