基于FSDPC_Otsu算法的滚动轴承故障研究
2021-12-29邢婷婷孙登云樊凤杰
邢婷婷,关 阳,孙登云,孟 宗,樊凤杰
(1. 燕山大学河北省测试计量技术及仪器重点实验室, 河北 秦皇岛 066004;2. 唐山工业职业技术学院, 河北 唐山 063000)
1 引 言
滚动轴承作为机械广泛应用的支撑部件,对其进行状态监测与故障诊断具有重要意义[1,2]。轴承多故障耦合的复杂性,加大了诊断的难度。盲源分离利用其独特的优势成为新的故障诊断技术[3~5]。文献[6]提出扩展确定性随机分离方法,实现变转速下滚动轴承振动信号的盲源分离;文献[7]基于Gabor变换和盲源分离相结合的诊断方法,突破了源信号相互统计独立且最多只能有一个高斯信号的限制。在实际工况下,源信号数未知会存在观测信号数少于源信号数的欠定问题,而稀疏成分分析[8]是解决欠定盲问题的有效方法,因此被广泛应用到各个领域[9~11]。稀疏成分分析采用“两步法”,估计混合矩阵和估计源信号。估计混合矩阵作为第1步,其精度直接影响分离效果。根据聚类中心估计混合矩阵,给混合矩阵的求解提供了全新的思路,但是K均值聚类[12]与模糊C均值聚类[13]都存在依赖设置聚类中心初值的问题。
本文采用最大类间方差法[14,15],对于散点图中的混合信号进行阈值分割,降低信号的复杂度;再应用密度峰值聚类(clustering by fast search and find of density peaks,FSDPC)方法求解混合矩阵;然后通过L1范数最小化对混合信号进行分离,最后对得到的分离信号进行包络谱分析,提取故障特征,诊断故障类型。本文所提的聚类方法,既不需设置聚类中心的初值,又提高了对散点聚类的准确率和稳定性。
2 稀疏成分分析
盲源分离的数学模型可以表示为:
Y=AS
(1)
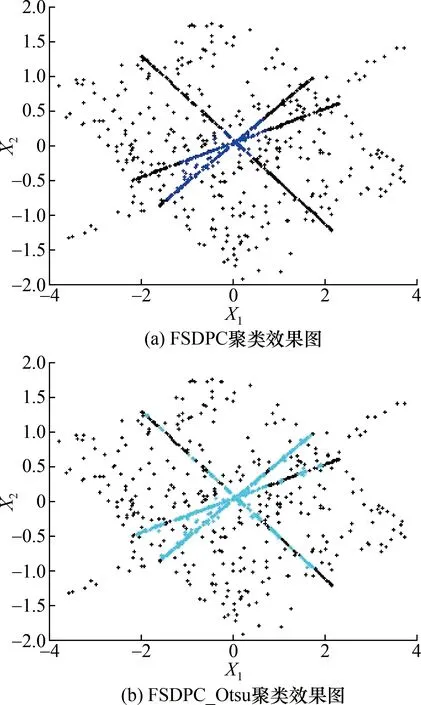
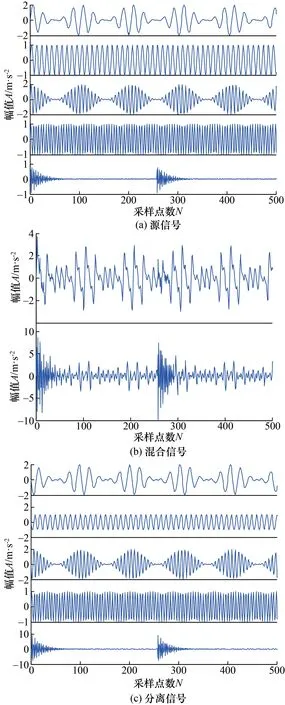
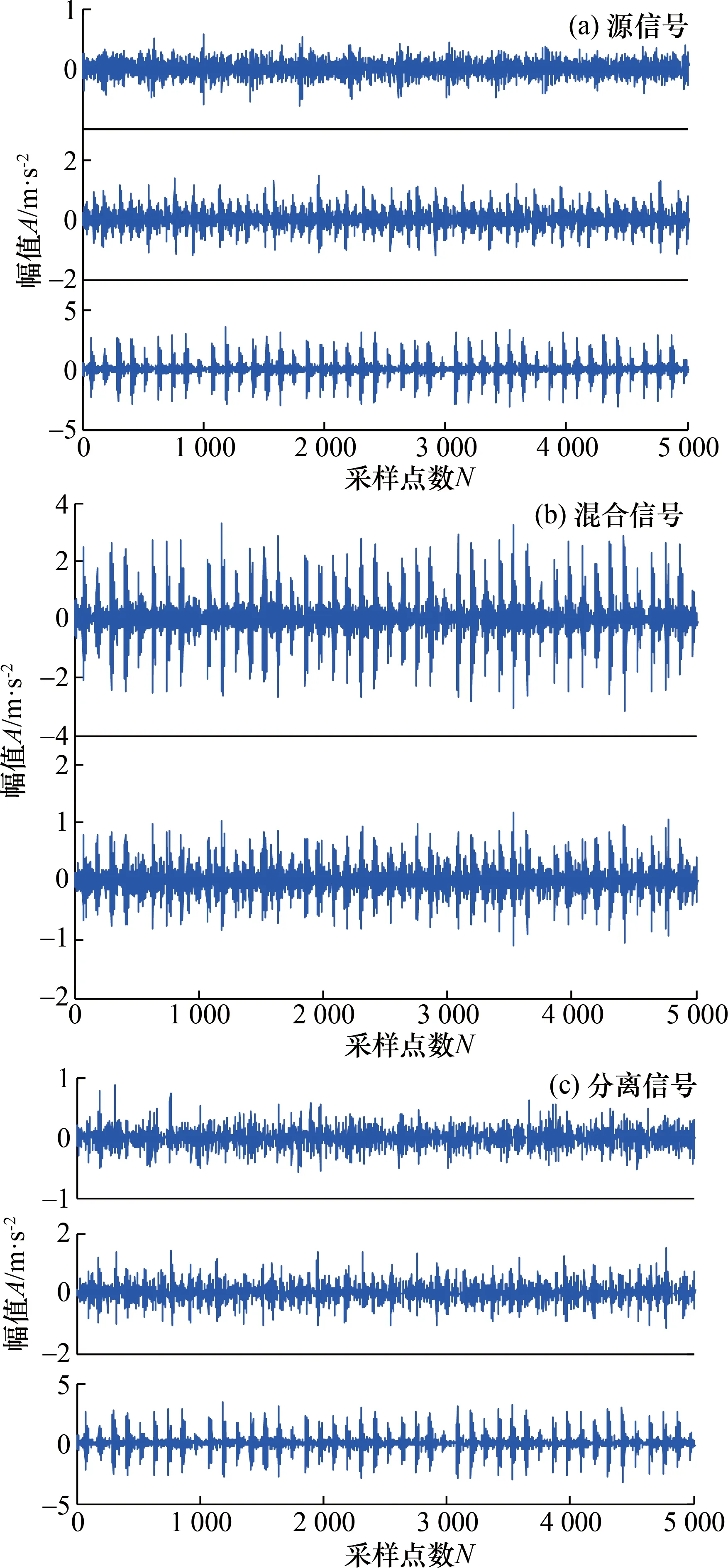
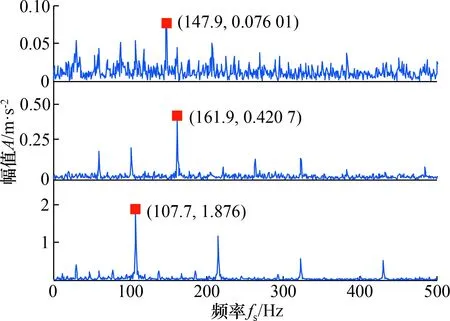
式中:Y∈RM×N为传感器获取长度为T的M个观测信号;A∈RM×N为混合矩阵;S∈RN×T为N个未知源信号。当M (2) 那么 (3) 令a(i+1)j/aij=ki,那么 yi+1(t)=kiyi(t) (4) 式(4)可以视为一条经过坐标原点的直线的表达式,这一过程为方向统一化。因此,只要源信号足够稀疏,观测信号的散点图将会聚成直线,可通过聚类方法估计混合矩阵A。在已知混合矩阵的基础上,使用L1范数最小化将求解式(1)的问题转化为优化的问题,从而得到源信号的估计。 设数据集P={pi},i={1,2,3,…,N},dij为点i与点j之间的归一化距离,ρi为数据点i采用高斯核计算的局部密度,以dij为基础,计算ρi和从点i到具有更高局部密度点的最小距离δi。 (5) (6) 式中:dc为截断距离,其选取遵循如下规则:设dij的个数为a,将dij按升序排列,令dc等于排列在0.02a位置的dij。 如果点i具有最高局部密度,则: (7) 根据式(5)~式(7),对数据集P中的每一个点i,计算得到它的(ρi,δi),并显示在平面图中,称之为决策图。根据决策图,选取同时具有较大ρi和δi值的点作为聚类中心。如果一点的δi较大,ρi较低,可以认为该点为孤立点,根据实际情况对该点进行去除,避免异常值对实验结果的影响。 由于混合信号复杂且散点图中各点的密度值的相似程度高,导致用FSDPC方法无法准确对信号进行聚类,从而影响混合矩阵的估计。针对这一问题,应用最大类间方差法[14]进行改进,在聚类前先对信号进行一次阈值分割,降低信号复杂度,提高算法的准确率和稳定性。 本文中最大类间方差法以决策图中每个点的密度值作为判断依据。对于待处理的数据集D,记背景点和目标点的分割阈值为T,目标点的点数占数据集D的比例为ω0,其平均密度值为μ0;背景点的点数占数据集D的比例为ω1,其平均密度值为μ1;数据集的总平均密度为μ,类间方差为g。 假设待处理数据集D的点的个数为M,图像中小于阈值T的像素个数为N0,大于阈值T的像素个数为N1,可得: ω0=N0/M (8) ω1=N1/M (9) N0+N1=M (10) ω0+ω1=1 (11) μ=ω0μ0+ω1μ1 (12) g=ω0(μ0-μ)2+ω1(μ1-μ)2 (13) 结合式(12)和式(13),得到类间方差的等价公式: g=ω0ω1(μ0-μ1)2 (14) 经过迭代,得到最佳阈值T,使得类间方差最大。经过改进后的FSDPC方法,能够将数据集内的点根据密度进行分割。对分割后的数据再进行聚类,聚类的准确率[16]将得到提高。 为了验证FSDPC_Otsu聚类的优越性,分别用2种方法对同一组信号进行聚类。对比FSDPC和FSDPC_Otsu算法的聚类效果,如图1所示。X1与X2各表示1路随机信号,由MATLAB生成的3路随机稀疏信号混合而成,采样频率为1 024 Hz,采样长度为1 000。排列紧密的点近似排列成3条过原点的直线,并尽可能多的将直线上的点聚为一类。图1(a)和图1(b)对比可知,FSDPC_Otsu算法能够将更多的点进行聚类。 图1 FSDPC与FSDPC_Otsu聚类比较图Fig.1 Comparison of FSDPC and FSDPC_Otsu clustering 为了更直观、严谨地对比2种聚类算法,引入聚类准确率,定量地对2种算法的聚类效果进行对比。聚类准确率用r表示,定义如下: (15) 式中:ai为最终被正确分类的样本数目;k为聚类数;n为数据集中的样本个数。聚类准确率的高低代表了聚类效果的好坏;当r=1时,表示聚类结果是完全正确的。 对50组随机数据的聚类实验结果的分析发现,FSDPC_Otsu的聚类准确率稳定在87%左右,数据是50组实验的平均值;而FSDPC的聚类准确率仅在43%到69%之间,数据是取50组实验中准确率较为稳定的47组的平均值。FSDPC_Otsu的聚类准确率更高,更稳定。 稀疏成分分析中的聚类方法有K-means聚类和FuzzyC-means聚类法,都存在依赖设置聚类中心初值的问题。FSDPC_Otsu聚类法最大的优势是能够不受聚类中心初值设置的影响,其在混合矩阵估计精度方面也优于其它2种方法。采用泛化交扰误差(generalized crosstalking error,GCE)作为混合矩阵估计精度的评价准则,定义如式(16)所示: (16) 式中:A为已知混合矩阵;A′为估计出的混合矩阵,A′B为估计出的混合矩阵与一个尺度矩阵和置换矩阵的乘积,∏为N×N维可逆矩阵组成的集合,这些矩阵每一列只有一个非零值“1”。GCE越小,表明A和A′越接近,估计的精度越高。 采用3路随机稀疏信号作为源信号,根据已知混合矩阵对源信号混合得到混合信号。分别通过FSDPC_Otsu、K-means和FuzzyC-means聚类算法估计混合矩阵,求出泛化交扰误差,进而评价混合矩阵估计精度,结果如表1所示。 表1 GCE结果比较Tab.1 Comparison of GCE results 由表1可知,FSDPC_Otsu方法估计混合矩阵的精度较好,且因其本身能够不受聚类中心初值设置的影响,算法优势凸显。 为了验证FSDPC_Otsu方法的可行性,采用仿真信号进行试验,混合矩阵估计的步骤如下。 方向统一化:根据稀疏成分理论,对混合信号进行方向统一化。 FSDPC_Otsu聚类:对方向统一化之后的混合信号进行聚类。 试验在混合矩阵已知的情况下对FSDPC_Otsu方法进行验证。构建以下信号进行仿真: s1=(cos(20 π t)+1)sin(100 π t) s2=sin(200 π t) s3=(cos(20 π t)+1)sin(300 π t) s4=sin(400 π t) s5=[s(1:256)s(1:256)s(1:256)s(1:256)] s=sin(800 π t)×exp(-50t) 采样频率为1 024 Hz,采样长度为1 024。为了更好地展示信号的特性,图2中的信号取0~500 s的点。源信号如图2(a)所示,s1和s3模拟2路不同频率的基波谐波信号,s2和s4模拟2路不同频率的基座振动信号,为使混合信号能够符合信号的单边振荡特性,在仿真信号中加入s5。按照已知混合矩阵的混合特性得到两路混合信号,混合信号如图2(b)所示,呈现出明显的单边振荡特征,符合机械振动信号的特征。图2(c)是分离信号,与源信号的相似程度较高。 图2 仿真信号试验结果图Fig.2 Simulation signals experiment result diagram 表2 仿真试验相关系数Tab.2 Correlation coefficient of simulation experiment 为了验证FSDPC_Otsu方法处理轴承故障信号的有效性,选用实际轴承信号进行试验。信号来源于美国西储大学旋转机械故障模拟实验台,轴承型号为6205-2RS SKF。实验与采集装置如图3所示,包括一个2马力电机(左侧),1个转矩传感器(中间),1个功率计(右侧)和电子控制设备。使用电火花加工技术在轴承上布置单点故障。试验中,电机转速为1 797 r/min,采样频率为12 kHz。在轴承上布置的故障直径为0.177 8 mm。 图3 实验与采集装置Fig.3 Experiment and acquisition device 选取的信号是驱动端传感器采集的内、外圈故障信号和风扇端轴承内圈故障信号。根据故障机理,计算得到风扇端轴承内圈故障特征频率为f1=148.2 Hz,驱动端轴承内圈的故障特征频率为f2=162.2 Hz,驱动端轴承外圈故障特征频率f3=107.4 Hz。3路故障信号,每路10 000个点组成3路源信号如图4(a)所示,根据已知混合矩阵得到的混合信号如图4(b)所示。根据混合信号估计混合矩阵,分离出源信号如图4(c)所示。 图4 故障信号试验结果图Fig.4 Fault signals experiment result diagram 表3可知分离信号与源信号之间的相关度较高,且保留了故障源信号中的故障特征频率。为证明故障特征频率未丢失,对分离信号进行包络谱分析,如图5所示。图5中,第1、2、3路信号出现的峰值分别是147.9 Hz、161.9 Hz和107.7 Hz,接近理论上风扇端轴承内圈故障特征频率148.2 Hz、驱动端轴承内圈故障特征频率162.2 Hz和外圈故障特征频率107.4 Hz。因此,分离信号保留了源信号的频率特征,能够通过分离信号进行故障识别与诊断。 表3 故障信号试验相关系数Tab.3 Correlation coefficient of fault signal experiment 图5 分离信号包络谱图Fig.5 Separation signals envelope spectrum 本文的FSDPC_Otsu估计混合矩阵方法,先用最大类间方差法对信号进行一次阈值分割,降低信号复杂度,减小噪声点和孤立点对聚类的影响;再估计混合矩阵。该方法既保留了FSDPC方法不需要设置聚类中心初值的优点,又能够提高对振动信号散点图聚类的准确率和稳定性,从而保证准确估计混合矩阵。通过仿真信号和轴承故障信号验证了方法的可行性,证明了方法能够估计出混合矩阵,并实现对混合信号的分离。结果表明分离信号与源信号的相关度较高并保留了信号的特征频率,通过对分离信号进行故障包络谱分析,能够识别故障频率从而实现故障诊断。3 FSFDPC_Otsu聚类算法
3.1 FSDPC聚类算法
3.2 FSDPC_Otsu聚类算法
4 实验及结果分析
4.1 对比试验
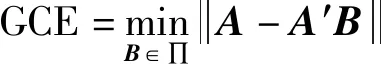

4.2 仿真试验
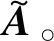
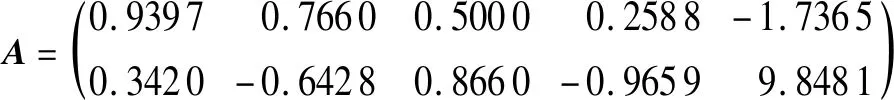
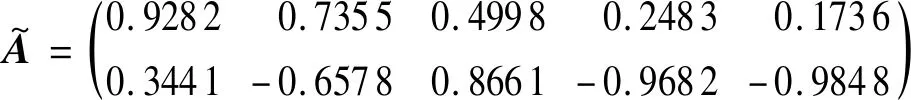

4.3 轴承信号试验

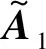

5 结 论
