基于圆柱矢量波函数对介质圆柱电型并矢格林函数的构建

雒向东,海 波,赵宇杰

(1.兰州城市学院 电子工程学院,甘肃 兰州 730070;2.甘肃高师学报 编辑部,甘肃 兰州 730070;3.兰州城市学院 信息工程学院,甘肃 兰州 730070)

圆柱体是工程应用中常见的电磁辐射与散射模型,这类电磁场边值问题的求解往往涉及圆柱矢量波函数的构建.在圆柱坐标系中用圆柱矢量波函数表示自由空间辐射或散射场是极为方便的,当获得自由空间圆柱矢量波函数展开式后,应用散射叠加方法可导出其他类型的并矢格林函数.应用并矢格林函数方法(简称DGF)解决电磁理论及工程边值问题,主要难点就是要构建并矢格林函数,对这一问题国内外学者已做了大量研究[1-7],如对规则形状波导、常用坐标系等问题已有一致的结果,有些问题如介质圆柱散射场等问题研究报道文献就比较少.在圆柱坐标系中依据圆柱矢量波函数,从自由空间构建的并矢格林函数出发,推证出介质圆柱内外空间的第三类电型并矢格林函数,该函数可为基于DGF方法解决介质圆柱形物体散射场等问题提供理论依据.

1 圆柱矢量波函数的基本理论

(1)

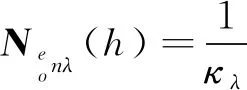
(2)

式(1)中双行符号是同时表示两个式子的一种符号表示方法，实质上是指下面两个式子

其他双行符号式子含义同此,式(1)和(2)中下标“e”表示偶函数，“o”表示奇函数。式(1)和(2)在整个空间区域(∞>r≥0，2π>φ≥0，∞>z>-∞)均有定义，且满足以下正交归一性[8]

(3)

(4)

(5)

式(3)～式(5)中积分区域为整个空间,本征值h和λ为连续取值.

2 自由空间并矢格林函数

(6)

和无穷远处的辐射条件,其表达式为[4]

(7)

式(7)中G0(R，R′)为三维标量波动方程的自由空间格林函数，R′表示源点位置矢量，R表示场点或观察点的位置矢量，具体为

(8)

(9)

(10)

(11)

(12)

(13)

(14)

将式(12)代入式(6),利用式(13)和式(14)可得

(15)

(16)

式中，

(17)

取积分回路沿上半λ平面的半无限圆路径,利用留数定理完成积分,式(16)计算结果为[4]

(18)

式中，

(19)

(20)

(21)

式(21)中上行符号对应r>r′,下行符号对应r

3 构建介质圆柱内外空间的电型并矢格林函数

(22)

式(22)中μ、ε分别表示介质柱磁导率和介电常数,它们可以是实数也可以是复数.基于两媒质分界面存在透射和反射效应,第三类电型并矢格林函数可设为

(23)

(24)

(25)

(26)

式(25)和式(26)中同一激励函数项中包含了奇偶相反的M和N的叠加,这一特点是边界条件所要求的[10].

为了求得待定系数A、B、C、D和a、b、c、d,应用在r=a柱面边界条件

(27)

(28)

可得到待定系数的16个线性代数方程,求解这些代数方程便可得到16个待定参数.

由式(27)可得

(29)

将式(21)、式(25)和式(26)代入式(29)得

(30)

由式(30)可推得两个基本方程

(31)

(32)

由(31)式得

(33)

进一步推得

(34)

式(34)满足下式

k1=κη,k2=κξ.

(35)

由式(32)得

(36)

进一步推得

(37)

式(37)满足下式

k1=κη,k2=κξ.

(38)

将式(34)和式(37)合并得

(39)

将式(23)代入式(28)得

(40)

将式(21)、式(25)和(26)代入式(40)得

(41)

由(41)可推得两个基本方程

(42)

(43)

由式(42)得

(44)

进一步推得

(45)

由式(43)得

(46)

进一步推得

(47)

将式(45)和式(47)合并得

(48)

将式(39)和式(48)合并得总方程为

(49)

将式(39)和式(48)分别写成矩阵方程为

(50)

(51)

4 结语