半导体三量子点中的多透明窗口及弱光孤子的调控

佘彦超， 曾羽群， 张蔚曦 ，肖政国 ，王强

(1. 铜仁学院 物理与电子工程系， 铜仁 554300； 2. 集美大学 理学院， 厦门 361201)

1 引 言

近年来，包括量子阱(二维)，量子线(一维)，量子点在内的半导体低维材料在量子光学和非线性光学领域引起了人们广泛的研究兴趣. 其中，由于半导体量子点中的光场传播所引起的量子相干及干涉效应尤其受到世人关注. 这是因为其具有退相干时间长以及与冷原子介质类似特性(如分立能级)，易集成，并具有较大带宽等优点[1-6]. 这些优良特性使得半导体量子结构在量子通信及传输等领域有着极其重要的应用[7-12]. 许多有趣的光学现象，如电磁诱导透明，双激子相干光场的调控，巨克尔非线性等现象都已经实现[13-22]. 尤其是在传播中具有保持波形不变、 保真度高、 抗干扰能力强等优势的超慢光孤子(能以远低于真空光速的速度传播的光孤子，Ultraslow Optical Soliton)的实现使之成为量子通信和量子调控等领域的研究热点[23-25]. 如Yang等[26]提出了一种产生匹配慢光孤子对(matched slow optical soliton pairs)的新方法，即在固态单量子结构通过双激子相干效应来产生匹配慢光光孤子对. 最早的单量子点模型是通过忽略量子点链中点间的相互作用而得到的简化模型. 考虑最简单的点间相互作用就得到了所谓的双量子点分子模型[27-29]. 实验上，量子点间相互作用已经能通过加载门电压的方式实现并能有效调控. 在该新型结构中，许多复杂而有趣的现象被发现. 例如，Borges等人[30]发现了隧穿耦合效应并建立了一个有效破坏量子干涉的路径，即在吸收光谱中创建透明窗口. 这被称为隧穿诱导透明，因为这一透明现象主要是由点间隧穿效应引起的[31]. 我们之前的研究也发现在双量子点间外加垂直方向电场， 通过控制隧穿和电场强度实现了亮暗孤子之间的转换[32]. 最近实验研究表明，一个高度可调谐的半导体线型三量子点装置可在砷化铟单晶纳米线中实现[33]. 理论上，人们发现，三量子点分子中的双隧穿耦合效应将能有效增强体系的克尔非线性效应[34].

值得指出的是，在以前的文献中，对于量子相干和干涉的光学效应的研究大都仅涉及到点间隧穿的考虑[35-38]. 如， Eslami等研究三量子分子系统中光学怪波的鲁棒性以及图灵结构的双稳和多稳[37]；Luo等探索了三量子点系统中隧穿诱导透明和Autler-Townes双重峰和三重峰现象的谱特征[38]. 这些研究工作并没有考虑外部控制光对三量子点系统非线性光学效应的的协同调控. 基于此，在本文中我们采用半经典理论分析双点间隧穿构建非对称三量子点模型，同时利用两个外光场以调控量子点分子中的线性光学特性及光孤子的形成. 所谓半经典方法，即是把光场看成是经典的麦克斯韦电磁场而用量子力学理论描述三量子点系统. 结果显示，由于点间隧穿和外加控制光场之间的耦合效应，在吸收光谱中单隧穿诱导透明窗口因而变成了双隧穿诱导透明窗口. 不同于单点间隧穿效应构建的双量子点分子，由于系统中双点间隧穿效应的存在，双隧穿诱导透明窗口会进一步演化成隧穿诱导透明三窗口. 弱探测光在系统中的非线性演化，可以由一个复系数的非线性薛定谔方程描述. 考虑到点间隧穿耦合和外加控制光场协同调制形成的隧穿诱导透明效应，方程系数的虚部远远小于实部，从而得到描述孤子演化的标准非线性薛定谔方程. 通过研究点间隧穿耦合和外加控制光场对孤子振幅和群速度的调控，发现相比于外部控制光，点间隧穿耦合效应将能更有效的增大孤子的振幅并降低其群速度. 我们的结果可能提供了一种新颖而有效的调控手段来调节量子点分子系统中的与量子相干和干涉相关的光学效应，而量子点分子系统是可应用于光电器件如高效的单光子源，量子信息处理器等等.

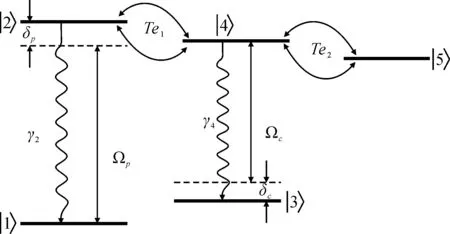
图1 非对称半导体三量子点分子系统与强控制场(半拉比频率为Ωc)及弱探 测场(半拉比频率为Ωp)相互作用的能级图. Te1，Te2分别表示中间量子点与左、 右量子点间的点间隧穿耦合强度. Fig.1 Energy-level diagram and excitation scheme of an asymmetric semiconductor triple quantum dot molecule system interacting with a strong control field (with half Rabi frequency Ωc) and a weak probe optical field (with half Rabi frequency Ωp). Here, Te1and Te2 represent the strengths of tunneling coupling between the intermediate quantum dot and the left and right quantum dot, respectively.

2 半导体三量子点理论模型及Maxwell-Schrödinger方程

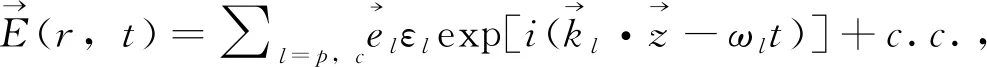
在我们的系统中，电子与电子之间的相互作用的影响被认为会比较弱，因此由于电子之间相互作用导致的多体效应在接下来的讨论中被忽略. 在相互作用绘景下，通过旋转波近似，系统的半经典哈密顿量可写成如下形式

〈3|+Te1|3〉〈2|+Te2|5〉〈4|+H.c.),

(1)

其中，H.c.表示哈密顿量的复共轭，Te1，Te2是点间隧穿耦合强度. 其中Δ2=δp,Δ3=δp-ω24,Δ4=δp-δ4,Δ5=δp-δ4-δ5. 在慢变包络近似和电偶极近似作用下，可得上述体系几率幅Aj的演化方程

(2a)

(2b)

(2c)

(2d)

这里dj=Δj+iγj(j=2～5)，而γj表示能级|j〉上衰减率，其值为γj=γij+Γij，其中γij和Γij分别代表能级寿命展宽和失相展宽. Γij表示能级|i〉↔|j〉之间的相移衰减，它受电子-电子散射，声子散射和弹性截面粗糙度的影响.γij表示能级|j〉的粒子数衰减，取决于系统的温度,随着温度的增加，其变化量级可从 μeV 到 meV[43].

对于外部光场用麦克斯韦方程描述，对于强控制场，我们不考虑他随时间及空间衰减，即认为是常数. 对于探测场，近似认为其振幅随时间的变化远小于光学频率，随空间的变化远小于光场(沿传播方向z)的波矢，从而得到

(3)

κ12=(Naωp|p12|2)/2ε0ħc为传播系数. 方程(2)和(3)组成描述探测光及耦合光与非对称半导体三量子点分子相互作用的Maxwell-Schrödinger方程.

3 线性光学性质

首先，我们研究该体系的线性光学特性，该特性主要对脉冲传播和衰减起作用. 为此，我们假设脉冲探测场远小于控制场，从而所有的电子最初几乎布居在基态|1〉，并令A1≈1.而Aj(j=2～5)和Ωp则正比于exp[i(Kz-ωt)]，利用Maxwell-Schrödinger方程，可得该系统的线性色散关系如下

(4)

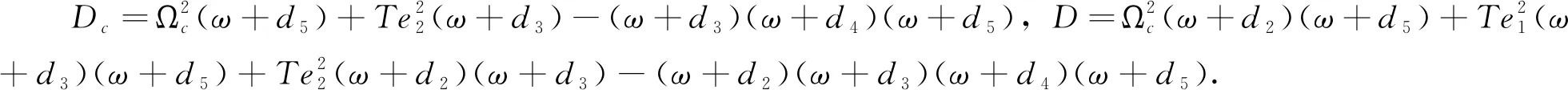
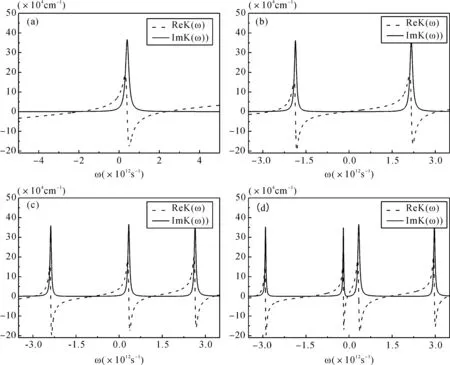
图2 探测场Ωp的线性吸收ImK(ω)(实线)和线性色散ReK(ω)(虚线)在(a) Te1=Te2=Ωc=0, (b) Te1=2.0 meV, Te2=Ωc=0, (c) Te1=2.0 meV，Te2=0, Ωc=1.5 meV,和(d)Te1=2.0 meV，Te2=Ωc=1.5 meV条件下随频率ω的变化情况. Fig. 2 The linear absorption ImK(ω) (solid curve) and linear dispersion ReK(ω) (dash curve) of the probe field Ωp as a function of the frequencies ω under the considerations of (a)Te1=Te2=Ωc=0, (b)Te1=2.0 meV, Te2=Ωc=0, (c)Te1=2.0 meV，Te2=0, Ωc=1.5 meV,和(d)Te1=2.0 meV，Te2=Ωc=1.5 meV. The other parameters used are given in the text.

只存在单峰值的Lorentz线型吸收峰，色散曲线在中心频率附近呈现负的斜率. 这意味着探测场在中心频率附近被极大地近共振吸收了. 这是由于此时的体系中点间隧穿强度为零，可视为由量子点基态和直接激子态所构成的二能级系统，因此当探测光与跃迁频率共振时，吸收谱线会在共振位置处出现极大吸收. 然而，对于弱隧穿强度(Te1=2.0 meV，Te2=Ωc=0)，吸收曲线[如图2(b)中的实线曲线]分裂成两个独立的吸收峰，两峰之间出现了一个深谷(在此情况下，隧穿诱导透明的透明窗口因此形成). 同时，色散曲线在中心频率附近呈现正的斜率. 这是由于弱的点间隧穿耦合的诱导，将使得导带能级|2〉和|4〉形成缀饰能级. 而探测光跃迁至两缀饰能级时会形成两条相干跃迁通道. 这两条相位相差π的跃迁通道使跃迁出现相消干涉现象，从而导致探测光的吸收谱线在原共振处出现吸收被抑制的深谷. 当控制场存在时，探测场的线性吸收如图2(c)实线所示，取控制场Te1=2.0 meV，Te2=0，Ωc=1.5 meV，对比与图2 (a)中的实线, 在吸收曲线中，将在ω=-2.5×1012s-1和ω=2.6×1012s-1附近出现两个新的吸收峰. 此外，在中心角频率(ω=0)附近会有一个吸收峰. 因此，在光学吸收在会形成两个深谷[形成双隧穿诱导透明的透明窗口]. 它是来源于点间隧穿和控制场与量子点分子的相互作用，能级|3〉和|4〉形成了动态的Stark劈裂，该劈裂导致相应能级劈裂进入暗缀饰态. 这导致隧穿诱导透明结构，因而在系统中出现双隧穿诱导透明窗口. 同时，色散曲线在中心频率附近再次呈现负的斜率. 随着双点间隧穿通道打开，Te1=2.0 meV，Te2=1.5 meV，Ωc=1.5 meV [如图2(d)实线所示]，原来在ω=-2.5×1012s-1和ω=2.6×1012s-1附近出现的两个吸收峰向两侧移动，透明窗口宽度更宽. 同时在中心频率附近光学吸收曲线再次出现了一个深谷，这意味着光学吸收曲线出现了三透明窗口. 从以上讨论中我们可以发现，半导体三量子点分子体系中隧穿诱导透明窗口的数量以及宽度可以由点间隧穿强度及外部控制光场协同调控. 有趣的是，图2(d)中色散曲线在中心频率附近再次呈现正的斜率，与图2(b)中所示的虚线相比，曲线更为陡峭，表明体系中的弱探测光可能实现超慢群速度传播. 从上述讨论可以看出，在三量子点体系中，色散曲线斜率的正负变换可由在点间双隧穿及外部控制光场的协同调控，进而实现正常色散和反常色散的变换.

4 非线性包络方程及超慢光孤子

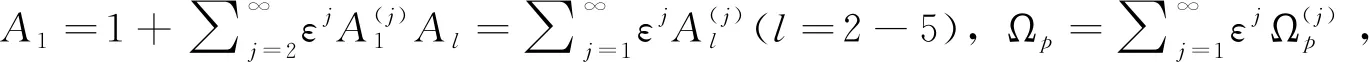
(5a)

(5b)

(5c)

(5d)

(5e)

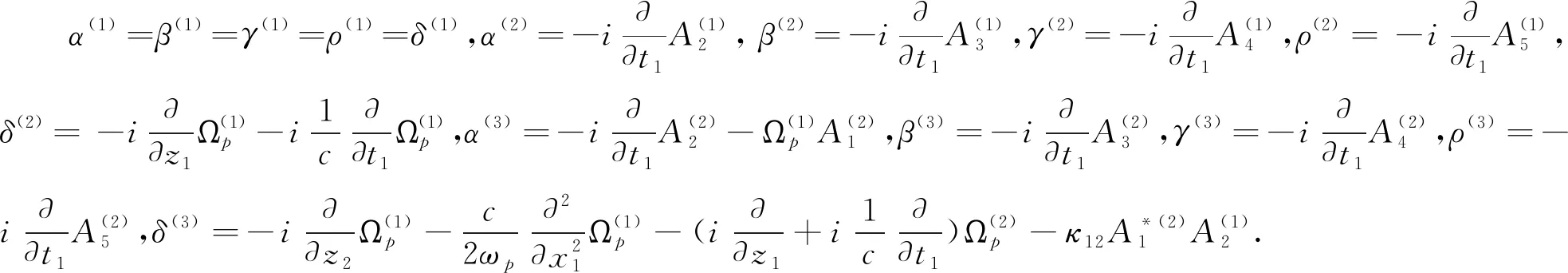
对于一阶情况(l=1),可得

(6a)

(6b)

(6c)

(6d)

(6e)

其中F是待定的包络函数，它的自变量是慢变量zl(l=1,2)和t1.

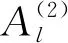
对于三阶情况(l=3)，消除久期项可以得到：

(7)

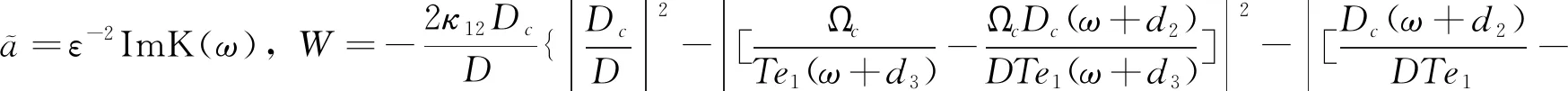
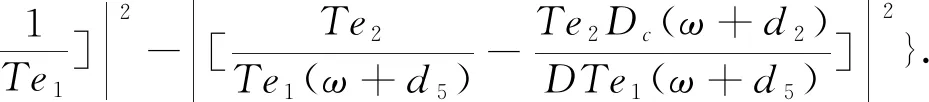
W|U|2U=0.

(8)

方程(8)是一个复系数的非线性薛定谔方程，方程左边最后两项分别表示体系的群速度色散效应和克尔非线性效应. 该类方程在非线性光纤和相关介质中均有相关的研究[39,40]. 通常情况下，这类复系数方程是不可积的，难以得到其精确解析解. 但如果其系数的虚部远远小于实部，其将可能得到孤子解. 之前的研究表明，体系在点间双隧穿和外部光场的协同调控下，将出现三透明窗口. 点间双隧穿和外部光场诱导的量子干涉相消，体系对探测光共振吸收将可能被极大的抑制. 这意味着选择合适的参数，体系的群速度色散系数和克尔非线性系数的实部将可能远远大于虚部. 接下来，我们参照图2中的参数提供一个实际的数值例子对方程系数进行进一步的比较，如图3所

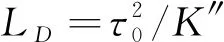
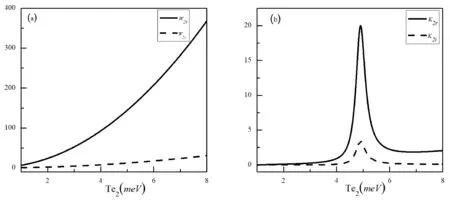
图 3 群速度色散效应参数K2 (a)及克尔非线性效应参数W (b)的虚部(如图中虚线)与相应的实部(如图中实线)随隧穿耦合强度Te2的变化关系. Fig.3 The imaginary parts (dashed curve) and the corresponding real parts (solid curve) of the group-velocity dispersion coefficient K2 and Kerr onlinearity coefficient W versus the tunneling coupling strength Te2.

(9)

通常d0<<1,ddiff<<1，因此上述方程可简化为标准的非线性薛定谔方程：

(10)

其单孤子解为：u=sechσeis代回初始参量得到：

(11)

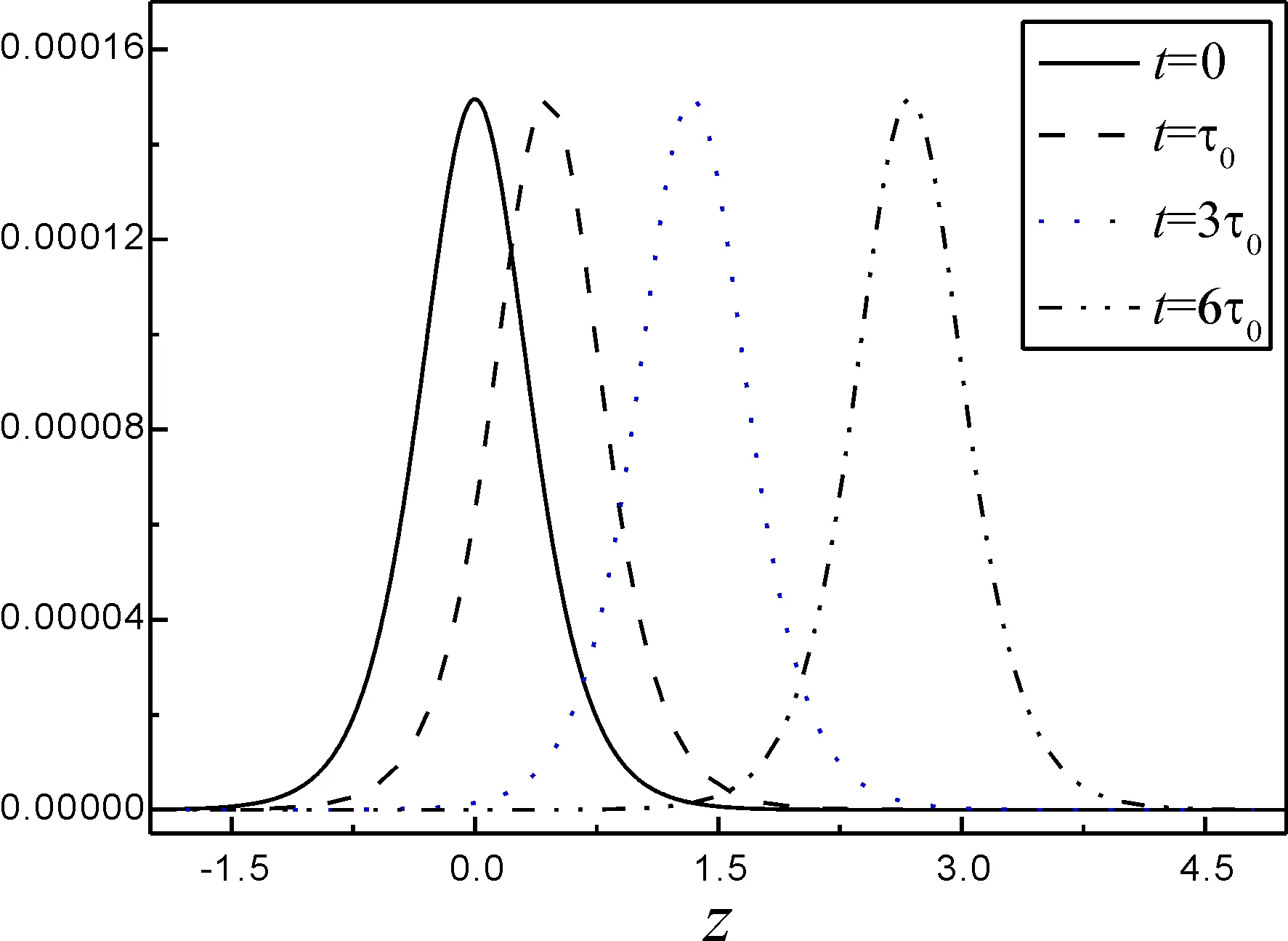
图4 时间光孤子的稳定性分析Fig. 4 Stability analysis of temporal optical soliton

为了研究点间隧穿耦合强度对光孤子的影响，首先我们检验时间光孤子传播的稳定性，仍选点间隧穿强度为Te1=3.5 meV，Te2=5.0 meV，其他参数和图2一致. 以(11)式为初始条件代入原始方程，给出不同时刻探测光强度随距离的传播情况如图4所示. 可以看出，在初始时刻，探测光在z=0位置形成一完美对称的包络波，该包络波显然为一亮光孤子. 随着时间的推移如t=τ0和t=3τ0，可以看到该亮孤子能保持波形的幅度和宽度不变，且稳定地向右传播，当 时 间 进 一 步 推 移 至t=6τ0时，孤子的幅度和宽度仍能保持不变地向右传播. 这说明非对称半导体三量子点中能产生时间光孤子，并可稳定地传播.

图5给出了在不同的外部控制光的条件下，光孤子的相对振幅随着点间隧穿耦合强度系数Te1的变化情况. 当Ωc=1.0 meV 时，如图5中实线所示，随着点间隧穿耦合强度系数的增加，孤子的振幅呈先增大再减小随即再次增大并减小的波动变化趋势且在位置Te1=4.97 meV存在最大孤子振幅. 当外部控制光Ωc增大时，光孤子振幅随点间隧穿耦合强度的变化呈现出类似的趋势，但孤子振幅峰值降低，峰的位置发生左移，

图 5 不同外部控制光Ωc条件下，光孤子振幅随隧穿耦合强度Te2的变化. Fig.5 The amplitudes of optical solitons versus the tunneling coupling strength Te2 with different control fields Ωc.

如图5中虚线所示. 这意味着随着外部控制光Ωc增大，孤子最大振幅对应的点间隧穿耦合强度系数Te1减小. 此外，对于弱点间耦合情况(Te1<3.0 meV)，光孤子振幅随着外部控制光Ωc增大呈现出下降的趋势. 进一步，我们在图6给出了光孤子相对群速度[44](the relative group velocity,Vg/c)随外部控制光及点间隧穿耦合强度系数Te1的变化. 结果表明，在我们的体系中，光孤子群速度会比真空中的光速下降2个数量级以上，而且随着外部控制光及点间隧穿耦合强度的增强，还会进一步减慢，这表明在我们的体系中可以形成超慢光孤子. 同样，相对于弱点间隧穿耦合情况(Te1<3.0 meV)，在强点间隧穿耦合时，光孤子群速度随着外部控制光的增强迅速减慢. 上述结果表明，半导体非对称三量子点体系中，外部控制光场及点间隧穿耦合强度均能有效调控光孤子的振幅及群速度，但点间隧穿耦合强度的调控更为有效，这可能是由于点间隧穿耦合强度能直接影响量子点分子中激发态能级的干涉效应.

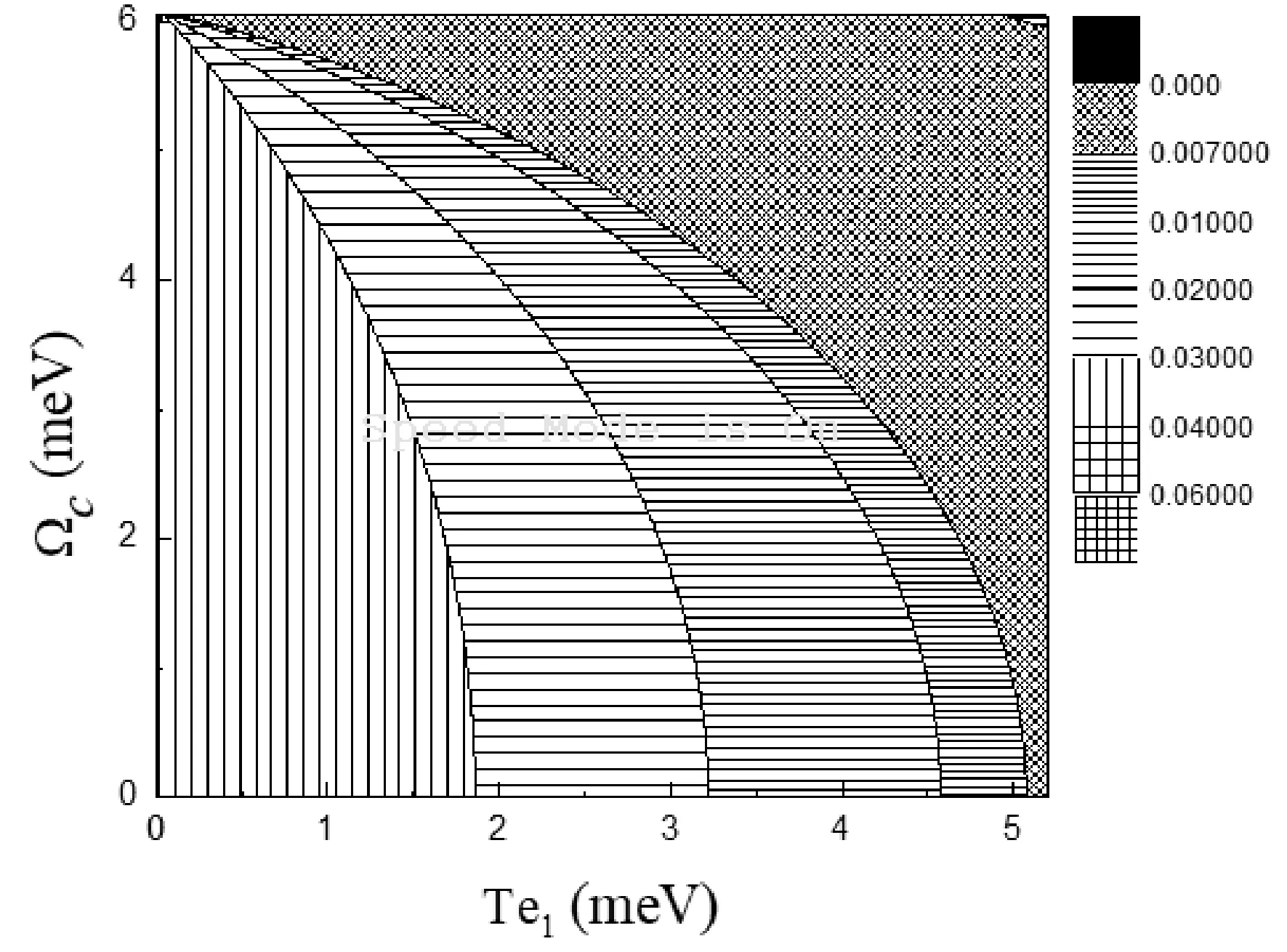
图 6 光孤子的相对群速度随外部控制光场Ωc及隧穿耦合强度Te1的变化. Fig.6 The group velocities of the optical solitons as a function of the tunneling coupling strength Te1 with different control fields Ωc.

5 结 论

本文中，我们研究了非对称半导体三量子点分子系统的线性光学特性及光孤子的形成，它是通过调控点间隧穿耦合及外部控制光场而得以实现. 线性情况中，当无光学控制场Ωc时，在适当条件下，由于点间隧穿耦合驱动量子相消干涉效应，系统会出现一个单隧穿诱导透明窗口. 透明窗口的宽度可通过改变点间隧穿耦合强度来调控. 特别地，在光学控制场存在情况下，由于控制场Ωc和点间隧穿耦合强度Te1，Te2的协同诱导而产生量子相消干涉效应，使得探测场的吸收曲线中出现三隧穿诱导透明窗口. 此外，从反常色散区域到正常色散区域的双开关可通过改变隧穿强度Te1，Te2及光学控制场Ωc而实现. 对于非线性情况，详细的多尺度分析给出了探测光场相应的演化方程. 我们发现系统的克尔非线性效应系数和色散效应系数的虚部远远小于实部，上述演化方程可以简化为具有孤子解的标准非线性薛定谔方程. 进一步地，发现光孤子的振幅随着点间隧穿耦合强度Te1增加呈现波动变化趋势且出现最大振幅. 这一振幅峰值随着外部控制光的增大而减小，且出现最大振幅的位置向弱点间隧穿耦合强度方向偏移. 点间隧穿耦合强度相较于外部控制光场，能更有效的减慢探测光场的群速度. 本文的结论将可能为涉及量子相干及干涉的光学效应的研究工作提供新颖和有效的思路. 此外，传统光电调制器件在有电压偏置的情况下，信号光场易被吸收而造成损耗. 在我们的系统中点间隧穿诱导透明效应将大大抑制信号光场的吸收损耗这将对于新型光电调制器件的实验实现也可能提供一定的理论指导.