考虑误差的行星滚柱丝杠副啮合模型研究

刘靖楠，范元勋

(南京理工大学 机械工程学院，江苏 南京 210094)

0 引言

行星滚柱丝杠的结构组成包括丝杠、多个圆周布置的滚柱、螺母以及保持架等。与滚珠丝杠相比，行星滚柱丝杠同样具有将旋转运动转化为直线运动的功能，且比滚珠丝杠具有更高的理论承载能力、使用寿命和使用可靠性[1-3]。但是与理论上的高承载能力相比，国产行星滚柱丝杠在实际使用上的表现不佳。影响行星滚柱丝杠承载能力的因素有很多，其中一个重要原因是由于滚柱制造安装时存在精度误差，导致滚柱各螺纹牙接触程度不同，有些螺纹牙甚至没有接触，大大影响了行星滚柱丝杠的承载能力与使用寿命。因此，进行滚柱偏斜时的啮合特性研究对提高行星滚柱丝杠副的承载能力与使用寿命有重要的意义。

目前，国内外对于行星滚柱丝杠的理论研究已有一定基础，而国内的理论研究主要集中在运动学分析、轴向变形、动态特性以及传动效率等方面[4-7]。在螺纹牙载荷分布方面，杨家军等[8]依据Hertz弹性接触理论，将滚柱作为整体，建立了刚度模型，得到了载荷分布与轴向刚度曲线;陈兵奎等[9-10]将滚动体等效成承受剪应力的矩形单元，建立了载荷分布计算模型并与有限元解进行对比。上述研究中，均假设行星滚柱丝杠副中的各滚柱的轴线与丝杠轴线平行，且各滚柱相对于理论位置未发生位移。

本文综合考虑行星滚柱丝杠副在加工以及装配过程中可能产生的各种误差，建立了考虑误差的行星滚柱丝杠副啮合模型，并运用高斯牛顿迭代法进行求解，与其他论文模型进行计算结果比对验证。结果表明：本文所提出的啮合模型结果可行，可以有效地对行星滚柱丝杠副零部件加工误差进行理论指导，为后续进行考虑误差的载荷分布模型研究打下基础。

1 行星滚柱丝杠副误差描述与分析

行星滚柱丝杠副的工作原理与行星齿轮轮系原理相类似，其结构如图1所示。

图1 行星滚柱丝杠副结构

1.1 螺纹参数误差

根据螺旋类零件加工误差的分析，螺纹类零件加工误差主要分为三类，即螺旋线分度误差、螺纹中径误差以及牙型误差。

1)螺纹中径误差

螺纹中径是通过螺纹轴向截面内牙型上的沟槽和凸起宽度相等处假想圆柱的直径，是确定螺纹几何参数和配合性质的基础参数。因此，螺纹中径误差是螺纹的一项重要技术指标。记中径误差为Δdi，其中i=s、r、n时分别表示丝杠、滚柱与螺母。

2)螺旋线分度误差

理论上，多线螺纹的各条螺纹螺旋线间的相位角是相等的，但由于加工时分度机构自身的制造精度、零件热变形以及操作误差等因素，螺纹上各条螺旋线间的相位角将产生误差值，如图2所示。

图2 螺旋线分度误差

3)牙型误差

牙型误差的定义为实际牙型轮廓与理想牙型轮廓之间的差值。图3中，虚线为理论牙型轮廓，实线为实际牙型轮廓，Δβi为螺纹牙侧角误差，Δci为螺纹半牙厚误差，Δr为滚柱圆弧半径误差。

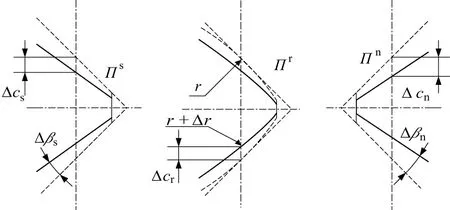
图3 牙型误差

1.2 滚柱定位误差

1)销孔定位误差

销孔位置偏差示意图如图4所示。

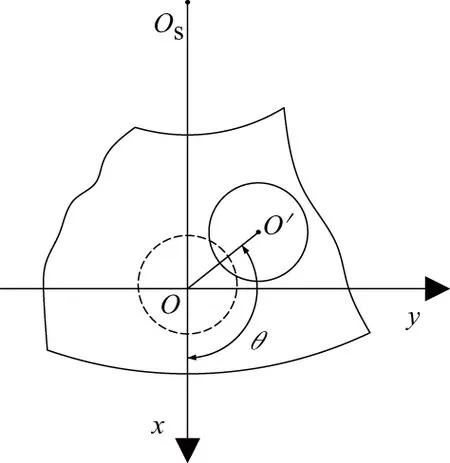
图4 保持架中销孔位置偏差示意图

2)保持架定位平面误差

定位平面误差引起的滚柱轴向偏差示意图如图5所示。

图5 滚柱轴向偏差示意图

3)保持架安装扭转误差

安装扭转误差引起的滚柱偏斜示意图如图6所示。

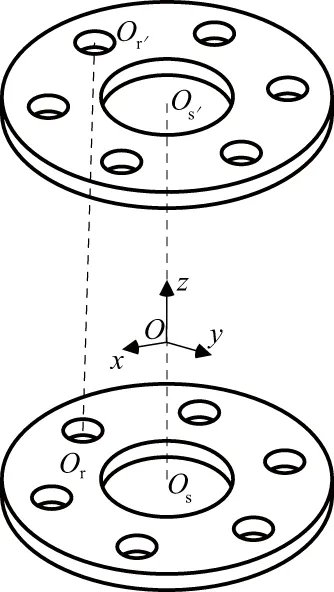
图6 滚柱偏斜示意图

2 行星滚柱丝杠副啮合模型

2.1 考虑误差的螺旋曲面方程

由于加工误差的存在，行星滚柱丝杠副的滚柱在实际工作过程中存在着旋转偏斜与位移偏斜两部分。这两部分偏斜参数，与前文所述各偏斜位移与中心线向量有关。行星滚柱丝杠副偏斜模型如图7所示。

图7 行星滚柱丝杠副坐标系

(1)

式中：OR′p为滚柱相对未偏斜坐标系的坐标；ORp为滚柱偏斜坐标系内的坐标；OR′ROR为滚柱相对于原坐标系的旋转变换矩阵。

根据刚体转动的欧拉定理，刚体有限转动下的旋转变换矩阵可表示其绕原坐标系各轴旋转角度的余弦矩阵的乘积。因此，滚柱相对原坐标系的旋转变换矩阵表现形式如下：

首先建立外螺纹的螺旋曲面方程。如图8所示，在外螺纹坐标系中，取螺纹中径上任一点O′，以O′为原点，垂直螺纹牙厚方向为x′轴,截面处与之垂直且与外螺纹轴线方向平行的另一坐标轴为z′轴，垂直截面的坐标轴为y′轴，以此建立相对坐标系。

图8 外螺纹相对坐标系

在坐标系O′-x′y′z′中，考虑误差的外螺纹牙截面方程的表示形式为

(2)

其中z的正号代表螺纹牙的上轮廓，负号代表下轮廓。

如图8所示，参考坐标系O′-x′y′z′可看作将螺旋曲面主坐标系O-xyz将原点平移至O′后，坐标系绕z轴旋转φ角而得到。其中φ为直线OO′在平面O-xy上的投影与x轴的夹角。因此坐标原点O′在主坐标系O-xyz中的向量参数为

(3)

式中：d为外螺纹的螺纹中径；L为螺纹的导程；Δd为中径误差。

根据参考坐标系中的螺纹牙轮廓方程与参考坐标系与主坐标系的变化关系，可得外螺纹的螺旋曲面方程在主坐标系中的方程：

(4)

其中：OΠ为主坐标系下的螺旋曲面方程；OT为参考坐标系与主坐标系的变换矩阵；Π为在参考坐标系下的螺旋曲面方程。

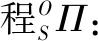
(5)

式中s、c分别为sin与cos缩写。

(6)

2.2 行星滚柱丝杠副啮合模型

由于行星滚柱丝杠副的接触类型为线接触，因此，为了在安装时便于装配以及使传动更加平稳，行星滚柱丝杠副的各螺纹间会留有一定间隙，因此可构建一个轴向间隙向量。根据啮合原理的描述，在传动过程中，两相切啮合点的法向量应保持平行，如图9所示。

图9 啮合条件

图9中，Γd与Γu为相啮合的两螺纹牙螺旋曲面,啮合点分别为点A与点B，两平面啮合点处法向量分别为nd与nu，轴向间隙向量k=(0,0,δ)，则相切啮合的接触条件如下：

(7)

式中ξ为常数。

由式 (7)中的曲面与间隙方程，可得

(8)

通过式(7)与(8)可得出含有5个不同的未知数的方程组，此即为两螺旋面间的啮合方程，可求解相啮合的两螺旋曲面间啮合与接触参数。

螺纹分度后的螺纹牙螺旋曲面可看做原螺旋曲面绕z轴旋转分度相位角后得到，左旋取正。所以，对于n头丝杠与螺母来说，其螺纹分度矩阵为

(9)

将螺纹分度误差带入螺纹分度矩阵中，并将分度矩阵左乘丝杠或螺母螺旋曲面方程，可得改进后的丝杠与螺母的螺纹牙螺旋曲面方程。式中，j表示第j条螺纹线。将式(5)与式(6)左乘分度矩阵，可得出改进后的行星滚柱丝杠副的丝杠与螺母螺旋曲面。将求得的螺旋曲面带入式(8)与式(9)中，即得出考虑误差条件下的行星滚柱丝杠副啮合方程。

2.3 模型算例验证

为了与已有论文的计算结果作对比，以表1的标准式行星滚柱丝杠副螺纹参数为例进行啮合方程求解运算。由于此计算未考虑任何偏斜误差，故表中未标注的参数皆取值为0。

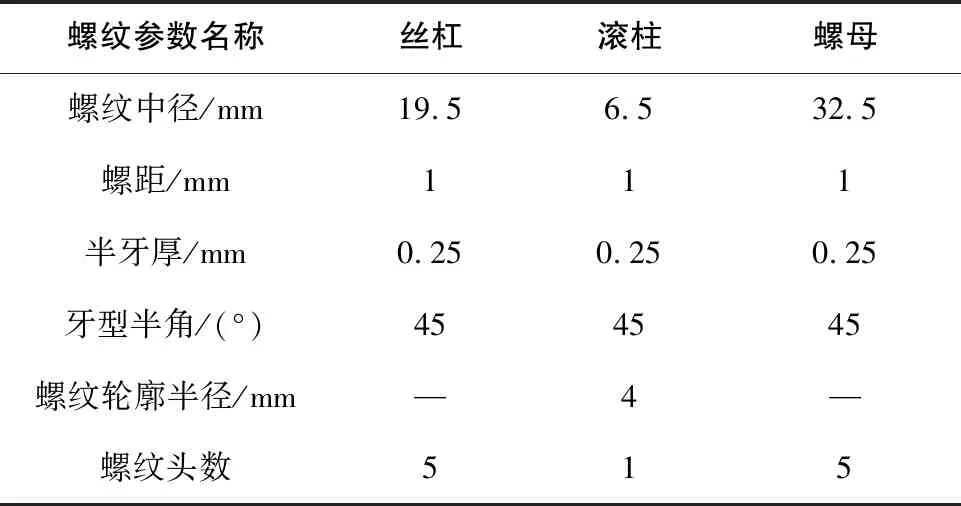
表1 标准式行星滚柱丝杠副螺纹参数

为了方便计算，选用x轴上的滚柱进行分析研究。在啮合时，丝杠的分头螺纹依次与滚柱螺纹进行啮合。运用Matlab软件进行迭代数值求解。取初值(0,0,0,π,0)，并设置终止条件ε=10-6，计算结果如表2所示(仅求解前5个螺纹牙的接触参数)。

表2 滚柱丝杠侧啮合接触特性计算结果

表中所求的轴向间隙与文献[11]中的是一致的，说明本文所建立的螺旋曲面方程与啮合方程在不考虑误差的情况下是正确的。

通过在Creo中建立行星滚柱丝杠副模型，并观察干涉量与间隙值，从而对考虑误差的啮合模型进行验证。装配模型如图10所示。

图10 装配模型

以丝杠螺纹中径误差分析计算为例进行验证，将带有丝杠螺纹中径误差的曲面方程带入式(7)与式(8)中，计算不同误差下丝杠与滚柱间的轴向间隙，同时建模分析三维模型的干涉量。计算结果如表3所示。

表3 不同丝杠螺纹中径误差下的计算结果对比

从表3中的干涉结果数据可以看出，随着丝杠螺纹中径误差增大，Creo中三维模型的干涉体积开立方后的数据也将增大，其变化趋势与本文所建立的啮合模型计算出的轴向间隙变化趋势基本一致，可说明本文所提出的考虑误差的行星滚柱丝杠副啮合模型是正确的。

3 结语

1)提出了一种考虑误差的标准式行星滚柱丝杠副啮合模型的分析方法，并经过算例计算三维模型验证其结果合理，方法可行；

2)通过算例分析表明，当考虑误差时，标准式行星滚柱丝杠副啮合点将发生变化，可能影响行星滚柱丝杠副传动精度及啮合平稳性；

3)本文采用的分析方法假定各滚柱偏斜参数一致，会引入一定误差；

4)本文采用的含误差的啮合模型分析方法可为进一步研究含误差的行星滚柱丝杠副运动学与动力学分析打下基础。