合成进口湍流方法在大涡模拟中的应用
2021-12-27刘俊杰仲冬冬葛宁
刘俊杰,仲冬冬,葛宁
(南京航空航天大学 能源与动力学院,江苏 南京 210016)
0 引言
与工程中常用的雷诺平均N-S方程相比,大涡模拟(large eddy simulation,LES)在理论上可以更准确地捕捉流场细节,对于分离和其他流动的模拟具有明显的优势。随着计算机硬件水平的提高,工程领域逐渐采用大涡模拟。与雷诺平均方法不同,对于湍流的大涡模拟,有必要在计算域的入口处提供最接近真实的瞬时湍流速度。研究表明,湍流的入口条件对平面射流、空间扩展的边界层流和后台阶流动有重要影响[1]。为了了解进口瞬时扰动速度设定方法的特点,研究大涡模拟对促进大涡模拟的工程应用具有重要意义。
为解决真实模拟的问题,KEATING A[1]、SAGAUT P等[2]发表的文献提出了许多解决办法。大部分都使用平均速度分解,指定了平均速度剖面,然后试图在平均速度上叠加真实的湍流脉动,这些方法叫做合成涡方法(synthesis eddy method)。这一系列方法的期望输出是一个非定常湍流流场,所呈现的流场信息为低阶统计量均值和均方根速度以及与之理想的两点时空相关性。低阶统计量均值较易匹配,而均方根速度以及与之理想的两点时空相关性相比较而言可能更难重建,因为它包括尺度和结构方面的信息。然而,这些重构是必要的,用以模仿真实物理机理存在于实际的壁面约束流动。通常来说,入流数据不具有这种性质,流动必须沿一定距离进行重构调整,通常用初始边界层厚度δ0来无量纲化。在δ0以下称为“自适应距离”,该距离决定了方法的性能,因为它确定了用于生成真实湍流计算域的流向长度[3]。
根据参考文献[1],入流方法可分为3类:回收调节法、前体数据库法和合成湍流法。基本上,回收调节法使用周期边界条件的变形,考虑到流体各向异性。在平板边界层的情况下,回收调节法的核心思想是根据湍流边界层的相似理论,将边界层下游回收平面的时均参数和脉动参数提取出来,根据边界层相似理论对参数进行调整,然后叠加到入口平面上,使入口湍流边界层保持合理的湍流脉动信息。这种方法的特别之处在于通过回收过程实现湍流脉动场建立在计算域的内部,从而避免了高额的计算负担。
前体数据库这种技术已被广泛应用,并在参考文献[3-4]中进行了修正,用以模拟大范围的流动。生成流入数据的更通用的方法是从单独的前体数据库中提取数据。通过提供适当的速度波动比例,数据库可以为各种配置和雷诺数提供数据。尽管如此,这些方法仍需要很大的存储容量。合成湍流法是收集所有合成湍流波动的方法,大多数情况下是通过随机序列进行的。然后,目标是修改这些序列,以使它们在数值或黏性耗散下不消失,并且其统计属性与实际流程的统计属性接近。LUND等使用一种基本的随机波动方法,根据该方法将目标雷诺应力分配给白噪声并引入作为入口。但该方法生成的数据既缺乏湍流结构又缺乏非线性能量传递。
本文提出了一种应用在大涡模拟计算中产生入流湍流条件的方法。这是JARRIN等人合成涡一种变形,是使用由雷诺应力张量的Cholesky分解的2阶矩来添加随机速度信号,信号由具有规定几何形状、随机符号和位置的湍流结构叠加而成。该方法对随机信号的定义进行了修正,使其可以分为几种模式,具有不同的时间、长度和速度尺度,也具有不同的涡度,中心思想是更真实地再现在湍流边界层流动壁面法线方向上的尺度分布。本文采用基于k-ωSST湍流模型,结合 WENO_ZQ高精度格式对平板同时模拟真实进口条件,获得了精细的流场结构,并利用涡识别方法和数值纹影图等流动显示方法识别流场。
1 数值方法
1.1 方法介绍
本文采用SANDBERG R D[5]提出的方法。这个便捷的方法是基于几个离散波数的叠加。在入口的3个速度分量中引入扰动,采用多个离散波之和。
u′(n,t,y,z)=I1(n)sin[f(n,t)]cos[g(t,z,n)]cos[h(t,y,n)]
v′(n,t,y,z)=I2(n)cos[f(n,t)]sin[g(t,z,n)]cos[h(t,y,n)]
w′(n,t,y,z)=I3(n)cos[f(n,t)]cos[g(t,z,n)]sin[h(t,y,n)]
(1)
谐波函数在时间t以及通过沿流向x的对流,俯仰方向z和跨度y方向的变量由下式给出:
f(t,n)=β1(n)t+φ1(n)
g(t,z,n)=β2(n)(z-φ2(n)t)+φ2(n)
(2)
h(t,y,n)=β3(n)(y-φ3(n)t)+φ3(n)
上述公式的每个参数都允许对入口扰动进行微调以获得湍流目标状态。可以使用频率β1(n)以及波数β2(n)和β3(n)来调整时间和长度刻度。计算域在螺距方向和跨度方向上是周期性的,这要求必须选择波数以使扰动满足相同的约束。β2(n)和β3(n)由下式给出:
β2,3(n)=2πk2,3(n)/p2,3
(3)
其中:p2和p3分别是俯仰方向和翼展方向的长度;k2,3是整数。翼展方向和俯仰方向的波数通常不一样。此限制不适用于β1(n)。可通过调整不同结构的入口方向来实现,最后可以使用ψi(n)指定相移。在每个方向上,使用系数Ii独立地调整湍流强度。在详尽的初步研究中发现,基于4种不同的波数组合j,总共使用16个波获得了良好的结果。表1中n、φ2、φ3给出了每个j的波数。每个波数组合j中的每一个波移动四分之一周期,相应的ψi由表1的其他参数给出。
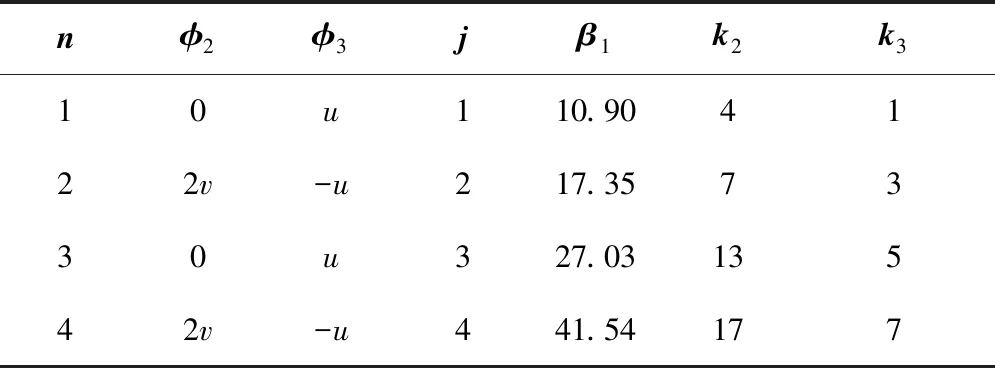
表1 湍流生成参数
1.2 求解器介绍
本研究内容是基于课题组自主开发的CFD求解器NUAA-Turbo2.0进行的,控制方程与数值解法详见参考文献[6]。求解器采用有限体积结构化网格、显式3阶龙格库塔(Runge-Kutta methods)和全隐式双时间步LU-SGS时间推进方法,同时发展了Roe和AUSM-up通量分裂方法、MUSCL、WENO_JS和WENO_ZQ等高精度方法重构界面量。
1.3 研究对象
选取一个经典的平板算例进行验证,参考Naguib实验数据[7]。出口为静压,绝热壁面为非滑移边界,周向为远场边界,跨度方向为周期边界条件。计算域和网格分布如图1所示。网格总量为420万。满足网格无关性要求。以进口边界层厚度δ作为计算参考长度。计算域为8.62δ×2.15δ×5.23δ[8],与实验模型一致,对应流动方向、展向方向和法向分别是网格在流向x和展向方向y上均匀分布;沿法线方向z在靠近壁面处进行加密处理,保证靠近墙的第一层高度z+≤1。频率值[9]模拟采用MPI技术,沿流向分成10个块进行并行计算。

图1 平板算例图
1.4 计算设置
计算采用基于SST 湍流模型的RANS方法进行模拟,然后在定常条件收敛下换用LES方法模拟进行非定常计算。同一研究对象采用同一套结构化网格,采用6阶中心差分格式处理黏性项,除RANS采用WENO 3阶格式外,其余都采用具有5阶精度的WENO_ZQ格式重构界面量。选取的物理时间步长可保证尾迹区CFL数≤1。
2 结果分析和讨论
湍流边界层(TBL)是自然界中广泛存在的一种复杂的流动结构。现有的湍流模型和流动机理主要基于不可压缩的湍流边界层,例如边界层分层理论,发夹涡理论和高低速条状结构。在湍流边界层中,发现湍流边界层没有呈现无序状态,但是相干涡结构维持了边界层的内部运动。根据经典的发夹式涡旋理论,当两个相邻的反向旋涡在下游发展时,将在旋涡头之间形成沿展向连接的涡旋结构,并最终发展成完整的发夹式涡旋结构。WU X H[10]在零压力梯度下对不可压缩湍流边界层进行了直接数值模拟,结果证实了发夹涡旋的存在,并且湍流边界层中的大多数发夹旋涡几乎是对称的发夹结构。
为了便于观察,用图2显示了通过Q准则识别的3D相干结构。不难发现,在湍流边界层的外层有许多发夹状涡流,并且大多数以不对称结构的形式存在。ROBINSON S K[11]指出,雷诺数对湍流边界层中涡旋的结构和状态有很大的影响。HEAD M R和BANDYOPADHYAY P[12]观察并总结了不同雷诺数下零压力梯度湍流边界层的相干涡结构:当动量厚度雷诺数(基于边界层动量厚度的雷诺数)<500时,总体涡旋结构较短,呈马蹄形涡旋或涡旋环。当动量厚度雷诺数>2 000时,涡旋结构呈现细长的发夹涡。结果表明,随着雷诺数的增加,发夹涡破裂并呈现出不对称的藤条结构。

图2 Q准则识别的三维拟序结构
图3显示了不同的雷诺数对发夹状涡旋拓扑的影响[13]。本文中,湍流边界层入口动量厚度雷诺数为400,属于低雷诺数。从图3可以看出,相干涡旋整体结构基本较短,呈现出马蹄形涡旋或涡旋环,与已有结论相符。
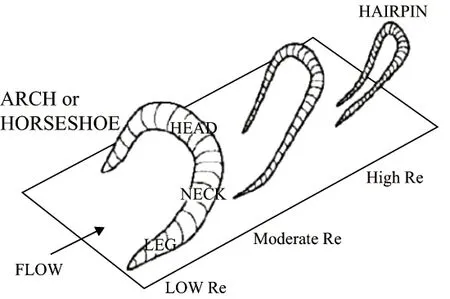
图3 雷诺数对相干涡旋结构的影响
图4为湍流边界层底部x+≈15处的流场云图。从图中可以清楚地看到沿翼展方向有高、低速交替带。这种结构被认为与湍流边界层的维持和发展密切相关。近年来,大量的数值研究证实了这种结构不仅存在于不可压缩流动中,而且存在于可压缩湍流边界层中。

图4 边界层底部的速度带结构
图5显示了流向方向在距进口截面约为8δ处沿法线方向的平均速度剖面。黑色实线表示此LES计算的结果。MORKOVIN M V[14]提出可压缩流边界层中的参数分布可以通过数学关系转换与不可压缩流中的参数分布联系起来。变换后的速度分布仍然满足经典的壁面定律分布,例如线性定律、对数定律和尾迹定律,这就是著名的Morkovin假设。

图5 计算的结果与先前发表的结果之间的比较
可以看出,在黏性底层和对数区域,LES得到的曲线与经典壁面律吻合较好。
线性律:
(4)
对数律:
(5)
以上公式中的参数由下面公式给出:
(6)
(7)
(8)
(9)
在经典的对数律中,k为Von Karman常数[15],其值为0.4~0.41,这里取0.41;C取5.25。动力黏度μw是温度的函数,可以通过Sutherland公式确定:
(10)
3 结语
对于湍流边界层的数值模拟,主要结论如下:在低声速湍流边界层中,流场中的拟序涡总体上表现出较短的整体结构,表现为马蹄形涡或涡旋环,这种结构取决于传入流的动量厚度和雷诺数。密度加权转换后的平均速度分布仍遵循经典的壁面律,例如线性律、对数律和尾迹律。
