基于二次调频小波变换的时变系统物理参数识别

赵宗爽，史治宇，张杰

(1.南京航空航天大学 航空学院，江苏 南京 210016；2.中国航发商用航空发动机有限责任公司，上海 201100)

0 引言

过去几十年中，针对传统时不变系统的动力学参数识别方法研究已十分成熟并逐步形成了一系列理论体系，按照识别过程中是否采用激励数据可将时不变参数识别方法分为试验模态分析(experimental modal analysis,EMA)及运行模态分析(operational modal analysis,OMA)两大类[1]。然而随着现代科技的突飞猛进和新兴领域的迅速崛起，实际工程结构中出现了越来越多的时变问题，譬如航天器中太阳能电池帆板和机械臂的展开问题；火箭和飞机高速飞行过程中，随着质量不断减小结构气动刚度随时间变化的问题；列车过桥时，随着列车位置的移动，车-桥系统的刚度和阻尼随时间变化的问题；随时间变化能自动调节结构参数的智能材料的使用问题等[2]。为了解决这类时变结构的动力学问题，研究时变结构的参数识别方法就显得尤其重要。

目前国内外学者对于时变系统参数识别问题的研究提出了一系列方法，主要可以归为两类：第一类方法主要基于短时时不变假设，应用具有局部时频分析能力的信号处理工具[3-4](短时傅里叶变换(STFT)、维纳分布(WVD)、小波变换(WT))或基于子空间模型进行参数识别，而此类方法在计算量和识别精度上难以兼顾，识别效率比较低。后有学者为解决此类问题引入了线调频小波分析工具[5]，虽有效提高了算法的识别精度和效率，但其仍是基于短时线变假设，对于非线性变化情况的识别并不理想。第二类方法是从信号的整体分解出发，自适应地将信号分解成多个本征模态函数，再对每个分量作参数识别，比较典型的就是希尔伯特黄变换(HHT)[6-8]。该类方法主要基于经验分解，缺乏充分的理论依据，且存在模态混叠、边界效应问题。基于以上识别方法的研究内容，结合时变系统的响应特性，在短时时域区间内通过二次多项式来拟合信号的频率变化，这种非线性的拟合方式相比于短时时不变和短时线变，可进一步增长分析时窗的宽度，降低迭代计算的次数提高计算效率。二次调频小波作为一种广义的小波函数能够很好地实现信号的非线性拟合[9]，同时由于多个调频参数的引入，对于信号在短区间内快变、突变的情况也能够精确刻画并追踪时变特性。

本文首先基于二次调频小波变换(QCT)结合时域滤波方法将多分量信号进行分解，在此基础上进一步推导了二次调频小波基函数的积分运算，通过测量结构加速度响应信号重构得出速度及位移响应信号，将时变系统微分方程转化为线性方程。结合分数阶模糊函数的相关特性[10-12]得出了二次调幅调频信号的相关性理论。在此基础上对激励和响应作自相关得到系统时变参数和响应相关系数之间的关系，进而实现结构时变物理参数的识别。最后通过仿真算例和相关实验验证了本文算法的正确性及实用性。

1 QCT及其函数积分运算

二次调频小波变换是将信号s(t)投影到一族二次调频小波基函数b(t0,a1,a2,a3)(t)上，b(t0,a1,a2,a3)(t)可定义为

b(t0,a1,a2,a3)(t)=w(t-t0)exp{j[a1(t-t0)+a2(t-t0)2+a3(t-t0)3]}

(1)

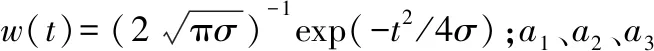
QCTb(t0,a1,a2,a3)=〈z(t),b(t0,a1,a2,a3)(t)〉=

a3(t-t0)3]}dt

(2)

(3)

对上式分部积分，结合基函数满足的两个特性将上式化简可得

(4)

由上式可以得出，对函数f(t)一阶不定积分的二次调频小波变换相当于对f(t)使用基函数的一阶原函数作为基函数进行二次调频小波变换，即

(5)

同理，函数f(t)二阶不定积分的二次调频小波变换可由f(t)使用基函数的二阶原函数作为基函数进行二次调频小波变换得出，即

(6)

2 时变系统参数识别

对于一个K自由度的线性时变动力学系统，其受迫振动可用下列方程来表示：

(7)

其中：M(t)、C(t)、K(t)分别为K×K的时变质量矩阵、阻尼矩阵和刚度矩阵；x(t)、u(t)分别为K×1的位移向量和激励力向量。

结合上节积分推导，时变系统微分方程可转化为线性方程：

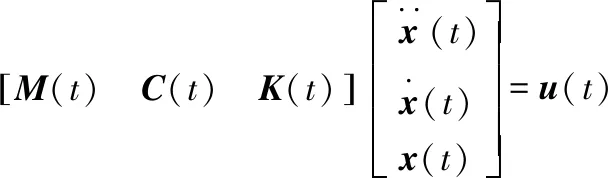
(8)

通过上式便能对确定性激励下的时变系统进行物理参数识别，但对于随机激励仍需对其相关性做进一步研究。分数阶傅里叶变换作为傅里叶变换的广义形式定义为

(9)

Kp(u,t)=

(10)

其中：Fp(u)为信号f(t)的p阶分数阶傅里叶变换；Kp(u,t)为核函数；p为分数阶傅里叶变换的阶数；α=pπ/2。结合其模糊函数的相关理论可得信号的自相关函数为

(11)

在得出以上二次调幅调频信号相关性理论的基础上，可进一步推导随机环境激励下时变系统的物理参数识别算法。

3 仿真算例

4自由度的弹簧阻尼时变结构如图1所示。系统的初始位移和初始速度均为0，结构参数随时间变化之前的设定如下：

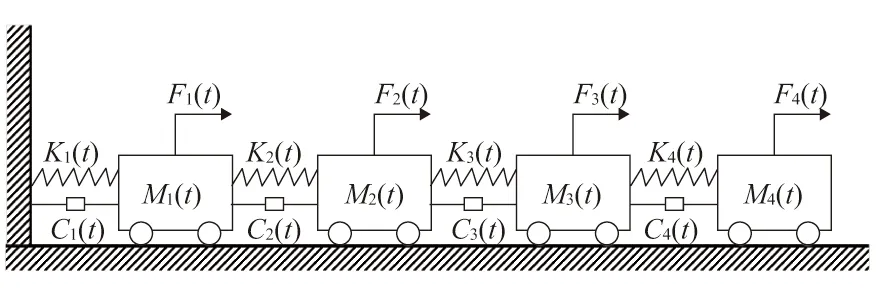
图1 4自由度系统示意图

(12)

对4个自由度均施加高斯白噪声激励，均值为0，方差为100，响应信号由Newmark-β计算，总的采样时间为t=20 s，采样频率1 200 Hz。为充分考察识别方法的有效性和可靠性，设置时变结构的质量系数和刚度系数随时间同时变化，且时变情况为线性变化、周期变化、二次函数变化、快速突变的组合，具体变化情况设置如下：

应用本文提出的算法对结构的时变参数进行识别，质量、刚度识别结果如图2、图3所示，从识别结果可以看出本文算法对于数量级较小的质量识别精度高、误差小，有效避免了与数值较大的刚度一同识别时质量识别误差很大的情况，表明本文算法具有较好的工程应用前景和实用价值。

图2 质量识别结果

图3 刚度识别结果

4 结语

1)本文基于二次调频小波理论，对时变结构响应信号的频率信息进行短时非线性拟合，结合二次调频小波变换将多分量信号分解为单分量的调幅调频信号；

2)提出了函数积分运算的二次调频小波变换计算方法，通过测量得到的时变结构加速度响应，将时变系统微分方法转化为线性方程；同时结合分数阶模糊函数的相关特性，推导了二次调频信号的自相关理论，得出了随机激励下时变系统物理参数的识别方法。

3)仿真算例中4自由度时变结构，质量和刚度参数的变化为线性变化、周期变化、二次函数变化、快速突变4种的组合情况，有效验证了本文所提算法的正确性。