基于稳健高斯滤波的磨损表面多尺度分析

张一兵,黄义涛，许家铭，刘立鹏，胡 瑞

(1.武汉理工大学 机电工程学院，湖北 武汉 430070；2.中车株洲电机有限公司，湖南 株洲 412000；3.南昌工程学院 机械与电气工程学院，江西 南昌 330000)

磨损表面形貌是摩擦副之间相互作用形成的微观形貌，其本质是表面微凸体之间的相互作用导致表面材料变形和剥落而形成凹凸不平的峰谷几何形态[1]，研究表明，由于磨损表面微凸体在大小和高度等方面具有不同的特性，因此组成的表面形貌具有多尺度特性，可从不同的尺度对表面形貌特征进行研究[2-3]。对具有多尺度特性、由不同频率或者波长的谐波组成的表面形貌采用的多尺度研究方法主要有以下几种：小波分析、滤波分析和分形研究等[4-5]。高斯滤波方法是国际标准组织推荐使用的一种滤波方法，在表面形貌多尺度分析中得到了较广泛的应用。Bataille[6]使用高斯滤波法研究了轧辊不同尺度表面形貌随轧制里程的变化规律，结果表明轧辊表面主要存在磨料磨损和粘着磨损，两种磨损分别影响不同频段的形貌；王春水等[7]使用motif和高斯滤波方法研究了AISI 304L不锈钢喷砂表面随尺度变化的规律，得出了最佳评价尺度为80 μm的结论，在此尺度下采用12个表征参数研究了喷砂距离对喷砂表面形貌的影响，结果表明Sku是指导喷砂工艺设计的最佳评价参数。但是高斯滤波方法存在边界效应和异常值引起的滤波基准畸变问题[8-9]，而稳健高斯滤波方法可较好地解决这两个问题，并在表面形貌多尺度分析方面得到应用。Marteau等[10]基于稳健高斯滤波方法，研究了喷砂和抛光对表盘表面形貌的影响，指出两种加工方式影响表面不同频段的形貌，并将两种加工产生的形貌特征从盘表面形貌中分解出来。由于磨损表面形貌的随机性高于加工表面，而磨料磨损和粘着磨损是常见的两种类型，并且两者的磨损形貌特征在不同尺度范围内存在较大的差异，因此需要采用稳健高斯滤波方法研究磨损表面中磨料磨损和粘着磨损形式下表面形貌的尺度特征，并将两种磨损形式的表面形貌从磨损表面分解出来，用于研究不同磨损形式对磨损进程的影响。

1 磨损表面多尺度滤波分析

1.1 磨损表面稳健高斯滤波

磨损表面三维形貌z(x,y)数据是由低频基准信息w(x,y)和高频粗糙度形貌信息(简称高频形貌信息)r(x,y)组成，对表面形貌数据进行稳健高斯滤波的过程，实际上是将表面形貌数据同高斯权函数和稳健权函数进行卷积运算的过程，滤波后得到式(1)所示的表面低频基准w(x,y)信息[11-12]，表面的高频形貌信息r(x,y)则可由原始轮廓信息减去低频基准信息得到，如式(2)所示。

ρ(ξ,η)dξdη

(1)

r(x,y)=z(x,y)-w(x,y)

(2)

式(1)中的三维高斯权函数的数学模型为：

(3)

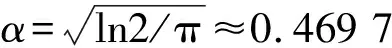
(4)

式中：c为调整参数；v为迭代估计残差，v=r/s，r为观测误差，s为尺度参数(这里以中位绝对离差作为尺度参数)。

1.2 基于稳健高斯滤波的多尺度分析方法

基于稳健高斯滤波方法，采用截止波长为尺度变量，对表面形貌数据进行稳健高斯高通滤波，得到对应于不同尺度的表面高频形貌信息，再对得到的高频形貌信息进行表面形貌特征的表征和分析，研究不同磨损形式表面与滤波尺度之间的关系。分析方法如下：①依据采样定理，由采样频率和采样尺寸确定截止波长的取值。因为测量仪在X和Y方向的采样频率为375 Hz和200 Hz，采样面积尺寸为4 mm×3 mm，所以截止波长的取值范围为0.02～3.00 mm，在此范围内分别取截止波长λ为：0.02，0.03，0.06，0.10，0.15，0.20，0.25，0.30，0.35，0.40，0.50，0.65，0.80，1.00，1.30，1.80和2.50 mm(由于摩擦运动轨迹方向为Y方向，因此只考虑X方向，式(3)中x和y方向的截止波长取λxc=λyc=λ)；②采用不同截止波长对表面形貌进行稳健高斯高通滤波,得到一组高频形貌信息；③选择算术平均高度Sa对滤波后的高频形貌信息进行表征，用于分析表面不同尺度的特性。

2 销-盘摩擦磨损试验

2.1 试样制备

摩擦磨损试验采用销-盘摩擦副接触试验方式。销试样的几何尺寸为：小径φ4×大径φ10×长度26 mm,表面粗糙度为Sa=0.780～0.852 μm，材料为Cr12MoV；盘试样的几何尺寸为：φ58×8 mm，表面粗糙度为Sa=0.612～0.869 μm，材料为35钢。

2.2 试验方法与试验

在XP-2型数控摩擦磨损试验机上进行摩擦磨损试验，得到磨合期、稳定磨损期和严重磨损期的盘试样表面形貌数据。在试验中盘试样固定在试验机夹具上，销试样在载荷作用下与盘表面相接触并进行回转运动。试验载荷为80 N,试验速度为0.21 m/s。试验前在盘试样表面需要采集数据的位置做好标记，然后添加0.04 ml的混合润滑剂开始试验(混合润滑剂：600XP150齿轮油和W60金刚石研磨膏质量比为15:1)。

选择磨损试验时间10.0 min，45.0 min，100.0 min，145.0 min，175.0 min和212.5 min为表面形貌数据采集时间点，使用自行研制的LSTM-1型磨损表面三维形貌测量仪采集盘试样磨损表面两个对称位置处的数据。采样区域为4 mm×3 mm，X方向采样频率和Y方向采样频率分别为375 Hz和200 Hz(采样间距分别为2.67 μm和5 μm)。每次采集完数据后，再使用原摩擦副继续进行下一个时间段的磨损试验，试验期间不再添加润滑剂。

图1为磨损试验中摩擦系数随时间变化的曲线。由图1可知，当试验时间在0～45.0 min之间时，摩擦系数波动较大，说明试验处于磨合期；试验时间在45.0～145.0 min之间时，摩擦系数较稳定，处于稳定磨损期；当试验进行到145.0 min之后，摩擦系数开始出现大的波动且急剧上升，说明试验进入严重磨损期。

图1 磨损试验中摩擦系数随时间变化的曲线

3 试验结果与分析

3.1 试验进程中表面形貌的变化规律

图2为盘试样表面某一标记位置在不同磨损时间点测得的表面形貌图。从图2可知，盘试样原始表面(时间为0 min时的表面)的纹理均匀，表面粗糙度Sa为0.66 μm；当磨损试验进行到10.0 min时，在磨损表面，波峰变得平缓，出现尺寸较大的沟槽和凹坑，表面粗糙度增大至3.68 μm；当磨损试验进行到45.0 min时，表面的峰谷均匀相间，峰和谷都较为宽大，呈现出明显的犁沟特征，表面粗糙度增大至7.38 μm；当磨损试验进行到100.0 min时，表面粗糙度为5.31 μm，表面的峰变得更加平缓，谷没有太大变化；当磨损试验进行到145.0 min后，表面粗糙度为6.79 μm，表面形貌与之前相比较峰的变化不大，但是沟槽增多；当磨损试验进行到175.0 min时，表面粗糙度为8.68 μm，表面的峰区域减少，沟槽增大增多，并且出现了较多的凹坑；当磨损试验进行到212.5 min时，表面粗糙度为9.52 μm，整个表面谷的比例增大，表面的峰变得不连续。

图2(a)为具有磨削规律纹理特征的盘试样原始表面形貌图。当磨损试验时间小于45.0 min时，摩擦副处于磨合期，由于试验中只添加了0.04 ml的混合润滑剂，表面处于边界润滑状态，由相互接触的微凸体组成的摩擦表面峰较尖锐，接触应力较大，容易发生变形和部分粘着现象，因此表面的峰变得平缓，同时表面出现凹坑；随着试验的继续，相接触的峰逐渐被挤压和磨损，表面凸起的峰变得更加平缓。另一方面，销试样表面微凸体和混合润滑剂中金刚砂颗粒的硬度都大于盘表面的硬度，会在盘试样表面产生划痕和犁沟，因此在该阶段主要发生磨料磨损和粘着磨损。磨损试验在45.0～145.0 min时间段时，摩擦表面的峰经过磨合阶段后已趋向于一个变化平缓的稳定磨损期。当摩擦表面的润滑剂不足以将表面相互隔离，盘表面起支撑作用的峰被磨平到一定程度时，销表面较高的峰和表面间的磨屑会再次加深盘试样表面的沟槽，因此在该阶段主要发生磨料磨损，如图2(e)和图2(h)的测量形貌和实际表面所示。当磨损试验在145.0～212.5 min时，摩擦表面的润滑油已经消耗殆尽，摩擦加剧、表面温度增高，在盘试样表面发生粘着，进而因粘着点的剪切和撕裂作用，在摩擦表面留下凹坑和瘢疤,说明此时摩擦副处于严重磨损期。从测量的表面形貌图2(g)和212.5 min的表面照片图2(i)中，可观察到摩擦表面由原来连续的峰变为断续的形式，并存在较多的沟槽和凹坑，表明此阶段发生了磨料磨损和粘着磨损。由以上分析可知，盘试样表面主要发生磨料磨损和粘着磨损，两种磨损形式在不同阶段可能具有不同的磨损率，为了研究两种磨损形式的磨损率，应设法将两种不同磨损形式的表面，从采集到的盘试样表面数据中分离出来，分别研究其变化规律。

图2 盘试样表面在不同磨损时间的测量表面形貌图及145.0 min和212.5 min的实物表面

3.2 磨损表面的多尺度分析与分解

利用稳健高斯滤波方法，采用不同的截止波长λ值，对盘试样磨损表面滤波后得到的高频形貌信息进行计算得到粗糙度Sa值，由此得到图3所示包含7个磨损试验时间的λ-Sa曲线图。由图3可知，Sa的变化趋势都是随着λ增大先增大，然后在λ=1.0 mm附近趋于稳定，表明在波长范围为0.02～1.00 mm时，Sa随截止波长的增大变化较大，因此需要对该频段的表面形貌信息进行深入分析。

图3 不同磨损时间盘试样表面Sa随λ变化曲线

针对图3中λ范围为0.02～1.00 mm的λ-Sa曲线，利用对数坐标变换得到双对数坐标下的λ-Sa散点和拟合直线图，如图4所示，其中盘试样原始表面的λ-Sa曲线在整个波长范围内为线性关系，说明经过磨削加工的盘试样表面具有分形特征，整个磨削表面形貌具有相同的多尺度结构。当磨损试验开始后，不同时间所对应的λ-Sa曲线以λ=0.20 mm为分界线，表面形貌中的高频段(λ=0.02～0.20 mm，简称表面高频段)和低频段(λ=0.20～1.00 mm，简称表面低频段)呈现两种不同斜率的线性阶段，说明磨损表面具有双分形特征，在分形理论中表明该表面具有两种不同的多尺度结构。

图4 不同磨损时间盘试样表面在双对数坐标下的λ-Sa散点图及拟合直线(λ范围为0.02～1.00 mm)

分形维数是描述具有分形特征系统的复杂性和相似性的参数，因此可通过计算盘试样表面形貌的高频段分形维数(DH)和低频段分形维数(DL)，对两个频段中不同磨损时间的形貌结构进行分析。参照文献[6]和文献[13]中由赫斯特指数计算分形维数的方法可知，图4中λ-Sa曲线的斜率为赫斯特指数，因此，分形维数D为：

D=3-赫斯特指数

(5)

图5为不同磨损时间盘试样表面高频段和低频段分形维数的柱状图，由图5可知：

图5 不同时间磨损表面高频段和低频段的分形维数

(1)盘试样原始表面高频段分形维数DH0和低频段的分形维数DL0相等，约为2.60。这表明磨削加工后的盘试样表面高频段和低频段具有相同的多尺度结构。

(2)不同磨损时间表面高频段分形维数DH都相近且等于原始表面高频段分形维数。这表明经过摩擦磨损试验后，盘试样表面的高频段形貌具有与原始表面相似的多尺度结构，说明摩擦磨损过程对高频段表面形貌的改变遵循与磨削工艺相似的作用机制，通过分析试验方法和表面形貌显微观察可知，这种作用机制是磨料磨损。

(3)不同磨损时间表面低频段分形维数DL相近，并且都小于原始表面低频段分形维数。这说明磨损后的低频段和高频段的表面形貌具有不同的多尺度结构。

利用波形的叠加特性和稳健高斯滤波方法，以λ=0.2 mm为分界点，将采集到的磨损表面形貌数据分解为高频段和低频段两种表面形貌，得到不同多尺度结构的表面特性。通过对磨损试验时间在10.0～212.5 min范围内采集的盘试样表面形貌分解后可知，分解后的低频段表面形貌之间具有类似的结构特征，而高频段表面形貌具有另一种不同的结构特征。

图6为磨损试验时间为212.5 min时，由盘试样表面形貌数据分解得到的高频段和低频段形貌图。从图6可知，高频段形貌的纹理结构与未磨损的盘试样表面相似，属于同一种多尺度结构，由此与前面磨损试验后表面的高频形貌是由磨料磨损造成的分析结果一致。在分解后的低频段表面形貌中，峰谷尺寸较大、存在明显的凹坑和瘢疤特征，呈现出典型的粘着磨损标志，可知低频段的表面形貌是由粘着磨损造成的。

图6 磨损时间为212.5 min的盘试样表面形貌及其分解的高频段和低频段表面形貌

3.3 分解表面磨损率变化规律分析

按图6所示的分解方法，将盘试样在磨损试验时间为10.0 min、45.0 min、100.0 min、145.0 min、175.0 min、212.5 min时采集的表面形貌数据，以截止波长λ=0.2 mm为分界点将表面分解为含高频段信息的磨料磨损表面和含低频段信息的粘着磨损表面，再应用积分法(以212.5 min的盘试样磨损为参考，采用称重法得到的磨损量为158.2 mg，采用积分法计算得到的磨损量为141.9 mg，误差为10.3%)分别计算不同磨损时间的磨损率以及不同磨损形式在总的磨损率中所占的百分比，如图7所示。由图7(a)可知，磨损率曲线包含磨合期、稳定磨损期和严重磨损期3个阶段：

图7 盘试样各磨损时间的粘着磨损率和磨料磨损率以及占总磨损率的百分比

(1)在0～45.0 min范围内，磨料磨损率变化较小，保持在0.56 mg/min左右，而粘着磨损率在10.0 min时为0.07 mg/min，之后略有下降。两种磨损形式的磨损率都大于各自稳定期的磨损率，说明摩擦副表面在磨损初期磨料磨损和粘着磨损都较为剧烈。

(2)在45.0～145.0 min范围内，两种磨损形式的磨损率都是先以较大幅度下降，然后趋向稳定，其中磨料磨损率稳定在0.23 mg/min，粘着磨损稳定在0.01 mg/min，两种磨损形式的磨损率都保持在稳定值，说明摩擦副逐渐转变为稳定期，表面的磨损较轻微。

(3)当磨损试验时间超过145.0 min时，磨料磨损率和粘着磨损率都以较快的速度上升，分别在212.5 min处达到最大值0.63 mg/min和0.16 mg/min，此时摩擦副表面的磨损进入严重磨损期。

图7(b)为盘试样表面粘着磨损率和磨料磨损率相对表面总磨损率的百分比随时间变化的曲线，其中磨料磨损率所占百分比在10.0～100.0 min的时间内，由88.68%上升到96.11%后，开始保持一段相对稳定时期。在145.0 min之后，磨料磨损率所占百分比开始下降，到212.5 min时达到79.27%。粘着磨损率所占百分比在磨损时间为10.0 min时为11.32%，之后一直下降，在100.0 min时下降至3.89%并趋于稳定，在145.0 min后再次增大，并在212.5 min处达到最大值20.73%。

由图7可知，磨损率变化曲线与图1所示摩擦系数变化曲线呈现的3个阶段基本一致，磨料磨损在试验全程中所占比例都较大，而粘着磨损在磨合期和严重磨损期具有相对较大的比例。虽然积分法计算得到的磨损量与称重法存在一定的误差，但能够说明磨损率变化的相对趋势。

4 结论

采用稳健高斯滤波方法对销-盘摩擦磨损试验过程中，不同时间点的盘试样表面形貌进行了多尺度分析。根据磨料磨损和粘着磨损表面形貌的尺度特征，应用稳健高斯滤波方法对采集的磨损表面形貌数据进行了分解，并分析了分解表面磨损率的变化规律，得到以下结论：

(1)采用稳健高斯滤波和多尺度分析得到的磨损表面粗糙度Sa随滤波截止波长λ变化的双对数坐标拟合直线斜率，以及计算得到的表面分形维数，可以识别和分解磨损试验表面形貌数据中不同磨损形式的特征表面。分解的分界点是λ-Sa双对数坐标拟合直线斜率发生转折处的截止波长。

(2)利用分解后的磨损试验表面形貌数据，计算不同磨损形式的磨损率及其在总磨损率中的百分比，将有助于定量分析磨损表面中不同磨损形式在磨损进程中的变化规律。