某水电站地下厂房区地应力场反演

程王润，张文春，刘 英

吉林建筑大学 测绘与勘查工程学院,长春 130118

0 引言

地应力或原岩应力即储蓄在岩体中未受扰动的应力,它不仅是影响岩体力学行为的主要控制因素,同时也是引起岩体变形和破坏的力源之一[1].在实际工程中,初始地应力是地下工程建设的主要计算参数之一,合理获取地应力的大小与方向是地下工程设计工作的重中之重.但是由于实际工程中有诸多限制因素,能获取的实测点数据相对有限,而少数测点的数据不足以支撑较大区域的工程地应力场分析[2].因此,如何在数量有限的实测数据基础上去反演并且分析工程区的初始地应力场,对于地下工程具有重大的实际意义[3].

目前,地应力场反演方法众多,主要有应力函数法、位移函数法、神经网络法、回归分析法、遗传算法等[4].20世纪80年代初,郭怀志教授等人提出了有限元数学模型回归分析方法.20世纪90年代中期, 朱伯芳院士在该方法的基础上进行了修订[5].从理论方面分析了将自重应力作为已知量的地应力反演.本文采用多元线性回归分析,考虑岩体自重、X向构造应力、Y向构造应力等3种工况作用.进行地应力场反演.

1 多元线性回归分析方法

(1) 计算原理. 按照多元线性回归分析的原理,将厂房区地应力实测点的6个应力分量回归值作为因变量,计算得出的对应6个应力分量为自变量[6],考虑岩体自重以及构造应力的作用,对应的回归方程应为:

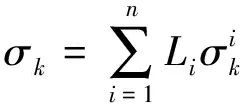
(1)

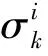
假设有m个实测点,则最小二乘法的残差平方和为:

(2)

由最小二乘法可知[6],要使残差平方和最小,对应的法方程式为:

(3)

由以上方程,求得待定回归系数L=(L1,L2,…,Ln)T,则计算区域内任一P点的地应力回归值为：

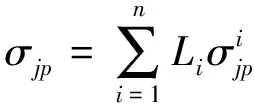
(4)

式中,j=1,2,…6,对应6个应力分量.

对于以上结果的合理性可进行显著性检验,首先给出实测应力分量的平均值:

(5)

式中,m为实测点数目;n为反演过程中考虑的工况个数.

(2) 复相关系数. 为检验回归效果，引入复相关系数，公式如下：

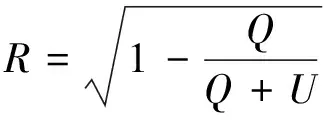
(6)

式中,U表示回归平方和;Q表示残差平方和,其计算公式如下:

(7)

(8)

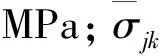
(3)F检验.F检验用于检验数据的回归效果，公式如下：

(9)

对于以上检验,当复相关系数R在0和1之间,越接近1,回归效果越好.当检验所得到的F>Fa(n,mn-n-1)时,则表示这n个自变量的总体效果显著[7].

2 工程概况

某水电站位于辽宁省.厂区建筑物主要由地下厂房、主变洞、进厂交通洞、通风洞等建筑物组成.厂房顶拱高程为264.8 m,底板高程为209.5 m,开挖尺寸为222.5 m×27.5 m×55.3 m(长×宽×高),属大型地下洞室.根据地应力测试结果,最大水平主应力值为10.91 MPa～13.94 MPa,最小水平主应力值为7.68 MPa～9.28 MPa,中间主应力为10.26 MPa～12.22 MPa;最大水平主应力优势方向为NE 79°,地下厂房区为中等地应力场.

厂房区主要有f 1,f 1,f 3,f 4,f 6,f 7,f 8等7条小断层和挤压破碎带J 4和J 1.其中f 3和f 4在地下厂房内出露,其余断层和挤压破碎带均分布于地下厂房外围.裂隙主要发育NEE,NWW和NW3组.其中,NE 70°～85°,SE∠65°～85°,结构面以平直光滑为主,部分平直粗糙; NW 310°～330°,NE(SW)∠75°～85°,以起伏粗糙为主,部分平直粗糙; NW 290°～310°,SW∠60°～85°,结构面以平直光滑为主,部分平直粗糙.

目前，地下厂房轴线选定方向为NW 295°,与第一组NE 70°～85°裂隙夹角为30°～45°;与第二组NW 310°～330°裂隙夹角为15°～35°;与第三组NW 290°～310°裂隙夹角为5°～15°.右侧避开了规模较大的断层f 1和f 2以及挤压破碎带J 4对地下厂房的切割,同时避开了左侧出水量较大断层f 8对厂房的切割.选定的厂房位置虽右侧受到了断层f 4的切割，但其规模较小，宽度仅为0.01 m～0.05 m，且倾角为80°，对洞室围岩稳定影响较小(故本文忽略断层影响),地下厂房工程地质条件总体良好,适合布置地下厂房等大型洞室.

3 初始地应力场反演

3.1 三维地质模型的建立

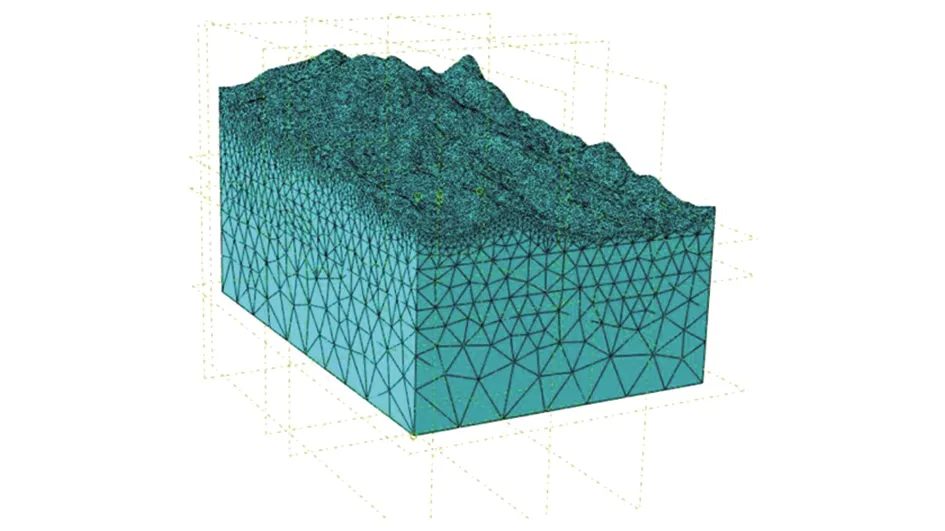
图1 三维数值计算网格Fig.1 3D numerical calculation grid

综合分析该水电站地下厂房区范围、地应力实测点的坐标分布以及相应水文地质资料和地形情况,运用笛卡尔坐标系建立坐标轴.平行于厂房轴线方向为X轴,垂直于厂房轴线方向为Y轴,垂直于XY所在平面且经过其交点的为Z轴.

整个计算区域X轴方向选取1 000 m,Y轴方向选取

1 500 m,Z轴方向地下取高程-150 m,至地表最高点高程900 m.计算区域确定后利用Rhino软件建立三维地质模型,然后导入大型有限元分析软件ABAQUS进行参数设置以及网格划分[8].整个三维地质模型采用四面体网格进行划分,单元类型C3D10M,一共划分478 449个单元,678 947个节点.计算网格如图1所示，具体岩体力学参数见表1.

表1 地下洞室围岩物理力学参数Table 1 Physical and mechanical parameters of surrounding rock of underground cavern

3.2 实测地应力分析

本次回归分析共有4个钻孔，即ZK309,ZK310,ZK310-1,ZK312.4个测点的实测数据见表2.

表2 各测点实测主应力值Table 2 Measued principal stress values at each measuring point

3.3 位移边界条件

本文一共考虑3种工况,如图2所示.

(1) 自重应力模型. 模型底部进行X,Y,Z3个方向的位移约束;对平行于厂房轴线方向边界施加Y向约束,X,Z方向自由;对垂直于厂房轴线方向边界施加X向约束,Y,Z方向自由.

(2)X向构造应力模型.模型底部所有节点进行Y,Z两个方向的位移约束,X方向自由;对X轴方向边界进行Y方向约束,X,Z方向自由;对Y轴方向边界,一侧取X轴方向约束,另一侧加载均布荷载σs1=1 MPa,方向沿模型沿Y轴法向水平加载.

(3) 向构造应力模型. 模型底部所有节点进行X,Z两个方向的位移,Y方向自由;对Y轴方向边界进行X方向约束,Y,Z方向自由;对X轴方向边界,一侧取Y轴方向约束,另一侧加载均布荷载σs2=1 MPa,方向沿模型沿X轴法向水平加载[9].

(a) 重力荷载模型边界条件

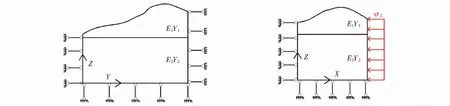
(b) X向构造应力模型边界条件

(c) Y向构造应力模型边界条件图2 各工况模型边界条件Fig.2 Boundary conditions of each working condition model

根据上述3种工况利用有限元软件ABAQUS建立如下3个有限元模型,如图3所示.

(a) 自重应力荷载有限元模型 (b) X向构造应力荷载有限元模型 (c) Y向构造应力荷载有限元模型图3 各工况有限元模型Fig.3 Finite element model of each working condition

4 地应力回归计算结果

初始地应力场主要由自重应力和构造应力组成.本次模型的岩体自重应力以体力形式施加,模型边界按上述分析施加.利用有限元软件ABAQUS,得到地下厂房区在自重应力下的主应力云图(如图4所示)、X向构造应力下的主应力云图(如图5所示)、Y向构造应力下的主应力云图(如图6所示):

(a) 自重应力下的最大主应力云图

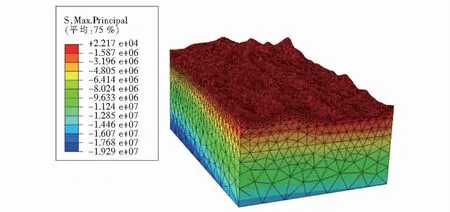
(b) 自重应力下的最小主应力云图

(a) X向构造应力下的最大主应力云图

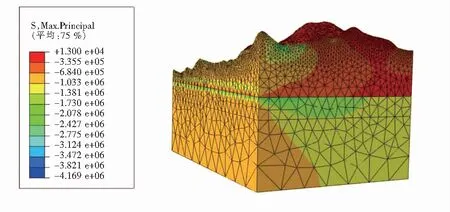
(b) X向构造应力下的最小主应力云图

(a) Y向构造应力下的最大主应力云图

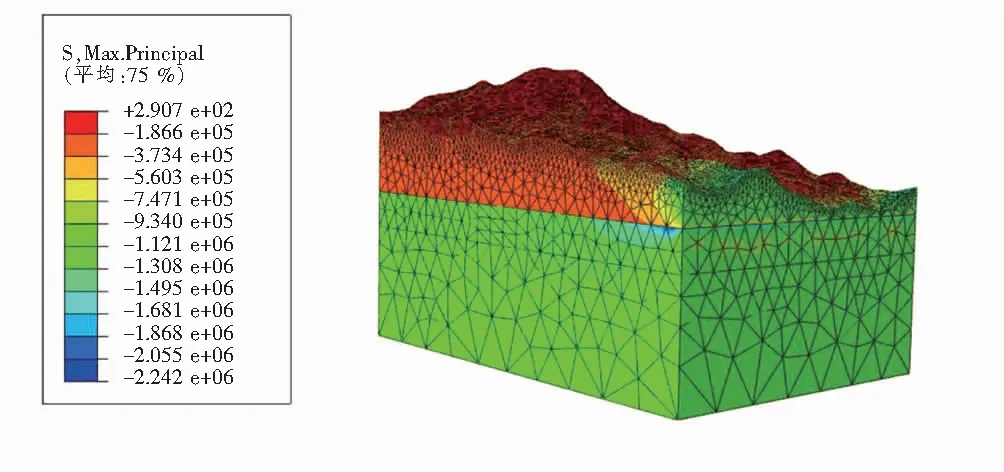
(b) Y向构造应力下的最小主应力云图

经过对初始地应力场多元线性回归分析，得到回归系数:L1=-1.788 5,L2=-4.787 4,L3=-5.372 9,观测误差ek=0.401 41.该电站地下厂房区的地应力场的回归结果为:

σ=-1.788 5σw-4.787 4σsl-5.372 9σs3+0.401 41

(10)

式中,σw为岩体自重应力引起的应力场,MPa;σs1为垂直于Y轴X向荷载引起的构造应力场,MPa;σs2为X轴Y向荷载引起的构造应力场,MPa;ek为观测误差,MPa.

实测应力分量与计算应力分量进行对比,见表3.

表3 各实测值与回归值比较Table 3 Comparison of measured values and regression values

经检验,复相关系数R=0.89,属于强相关,F检验中,显著性水平为α=0.05，检验通过,即表明本次回归计算所涉及的自变量整体是显著的.

5 结论

(1) 本文采用多元线性回归分析方法,考虑岩体自重、X向构造应力、Y向构造应力3种工况作用，对地应力的实测值和回归值进行分析,反演得到的初始应力场可以较好地反映地下厂房区地应力分布特征,结果具有较好的可靠性.

(2) 地下厂房区的地应力基本分布规律:最大水平主应力值为10.91 MPa～13.94 MPa,最小水平主应力值为7.68 MPa～9.28 MPa,中间主应力为10.26 MPa～12.22 MPa;最大水平主应力优势方向为NE 79°,地下厂房区为中等地应力场.

(3) 测区内最大水平主应力值(SH)>铅直应力值(Sv)>最小水平主应力值(Sh),最大水平主应力近NE～EW向,从地应力角度考虑,当最大水平主应力方向与地下厂房、隧洞等的轴线方向夹角为0°～30°时,有利于地下工程的稳定.