基于变论域模糊PID的供热系统设计和仿真

吕宝传，高晓红，董帅帅

吉林建筑大学 电气与计算机学院，长春 130118

0 引言

在太阳能供热控制系统中对换热器的二次网供水温度[1]控制要求比较高，如果控制不好会影响用户的供热温度，因此要保证用户稳定的供热量．针对温度控制系统的热惯性、非线性、时滞性[2]难以精确建立数学模型等特点，传统PID达不到系统控制要求，模糊控制针对非线性，时滞性系统模糊控制不需要精确的数学模型，但稳态误差较大，模糊PID可以根据模糊控制规则表对比例、积分、微分3个参数进行自整定，提高系统的动态性能和稳定性，但输入输出的模糊论域都是固定不变的，导致系统控制精度不高.文献[3]使用变论域模糊PID对永磁同步电机进行转速控制，使系统超调量减少，控制精度更高.文献[4]使用变论域模糊PID控制压铸机压射速度，使系统能精准控制电液伺服阀，响应速度快，无超调.变论域模糊PID在模糊PID的输入输出模糊论域增加动态伸缩因子，可动态调节输入输出模糊论域，具有自适应能力强，控制精度高等特点.为提高供热控制系统温度精度，使用变论域模糊PID控制器根据二次网供水温度偏差和偏差变化率实时调整输入输出的模糊论域[5]，并用Matlab中的Simulink仿真结果分析，验证变论域模糊PID控制具有更好的动态调节能力[6]和更好的自适应性.

1 太阳能供热系统原理

储水箱提供一次网恒定的供水温度，由二次网供水的供水温度传感器T3将采集到的温度反馈到PLC控制器中，换热器二次网供水温度T3是被控制量，一次网供水的流量为控制量，经过变论域模糊PID运算后，输出信号控制变频器的频率，再由变频器控制水泵的转速[7]，从而改变换热器一次网循环水流量，实现二次网供水温度的精确调节，并使二次网供水温度保持不变，提高供暖用户的供热量和供热效率．太阳能供热系统原理图如图1所示.

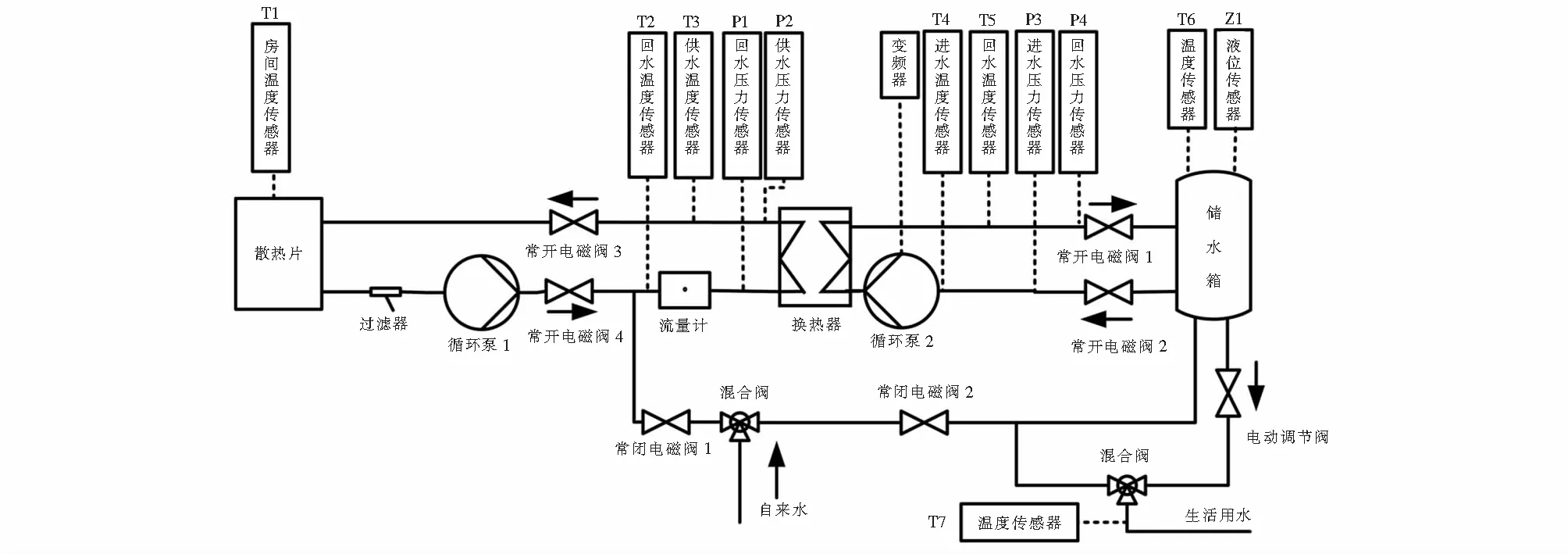
图1 太阳能供热系统原理Fig.1 Principle of solar heating system

2 变论域模糊PID控制器设计

2.1 数学模型建立

对于供热温度控制系统中的换热器热交换过程，需要对一次网水流量和二次网的供水温度建立数学模型，换热器热交换的数学模型[8]可以用二阶惯性环节和纯滞后环节表示，其传递函数：

(1)

式中，K为放大系数6.4；t1为惯性时间常数5.77 s；t2为惯性时间常数0.72 s；τ为滞后时间2 s；s为复变量.

根据换热器的具体参数，得到传递函数：

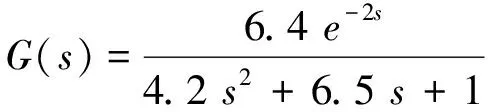
(2)

2.2 变论域伸缩因子设计

根据文献[9]采用基于模糊推理选择伸缩因子方法，偏差E、偏差变化率EC的输入伸缩因子和P，I，D这3个参数的输出伸缩因子可根据输入偏差和偏差变化率分别调整输入量E，EC和输出量P，I，D的模糊论域，实现输入输出量的自适应调整.变论域输入伸缩因子采用2个双输入单输出结构，输出伸缩因子采用1个双输入三输出结构，输入伸缩因子分别为α(e)和α(ec)，输出伸缩因子分别为β(P)，β(I)，β(D)．控制系统输入量偏差E和偏差变化率EC的模糊论域分别为[-E，E]和[-EC，EC]，输出量P，I，D的模糊论域分别为[-P，P]，[-I，I]和[-D，D]．当控制系统输入输出变量分别引入伸缩因子α(e)，α(ec)，β(P)，β(I)，β(D)，其输入输出的模糊论域分别为[-α(e)E，α(e)E]，[-α(ec)EC，α(ec)EC]，[-β(P)P，β(P)P]，[-β(I)I，β(I)I]，[-β(D)D，β(D)D]．输入变量E和EC的模糊论域[-6，6]，划分7个模糊子集{NB，NM，NS，ZE，PS，PM，PB}．α(e)和α(ec)伸缩因子的模糊论域分别为[0，2.1]和[0，1.3]，划分5个模糊子集{VS，S，M，B，VB}；β(P)，β(I)和β(D)的模糊论域分别为[0，50]，[0，13]和[0，60]，划分7个模糊子集{GS，VS，S，M，B，VB，GB}.输入输出变量伸缩因子控制规则见表1，表2.

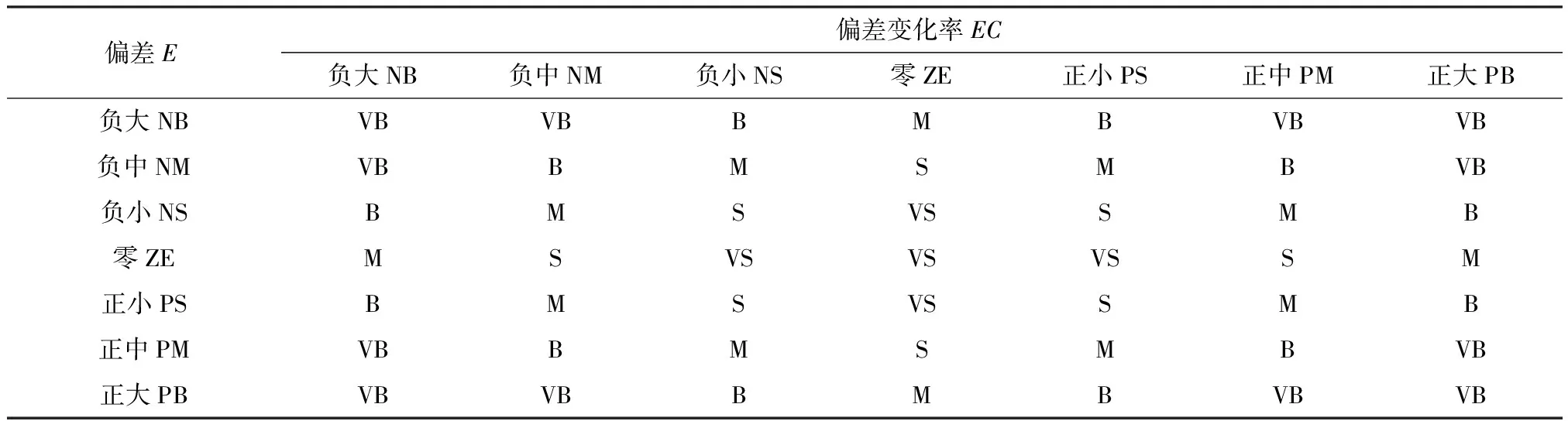
表1 α(e)和α(ec)伸缩因子模糊控制规则Table 1 Fuzzy control rules of flex factors α(e) and α(ec)

表2 β(P)，β(I)和β(D)伸缩因子模糊控制规则Table 2 Fuzzy control rules of flex factors β(P)，β(I) and β(D)

2.3 模糊PID控制器设计

模糊PID控制器采用双输入三输出[11]结构，输入量偏差E和偏差变化率EC的模糊论域[-6，6]，物理论域分别为[-40，40]和[-10，10]，输出量ΔKP，ΔKI，ΔKD的模糊论域[-3，3]，物理论域分别为[-2，2]，[-3，3]和[-0.9，0.9]，输入量化因子KE=6/40=0.15，KEC=6/10=0.6．输出比例因子UP=2/3=0.6，UI=3/3=1，UD=0.9/3=0.3．输入输出划分7个模糊子集{NB，NM，NS，ZE，PS，PM，PB}，隶属度函数采用对称均匀的三角形[12]形式，输入输出模糊规则[13]见表3，模糊推理采用Mamdani算法[14]，解模糊化采用面积重心法，得到输出量的精确值.

模糊PID参数计算公式[10]：

(3)

式中，kP，kI，kD为基准量，本文分别为9，10，7.2；ΔKP，ΔKI，ΔKD为模糊PID的输出变量；KP，KI，KD为经模糊PID修正后参数.

表3 KP，KI和KD模糊控制规则Table 3 Fuzzy control rules of KP，KI and KD

续表3

3 仿真和分析

3.1 变论域模糊PID仿真

对太阳能供热控制系统采用Matlab仿真实现，使用Simulink搭建供热控制系统，Saturation表示模拟量输出的数字量最小值0和最大值27 648，变频器表示将变论域模糊PID控制器的输出转化为0 Hz～50 Hz，从而实现换热器的热交换，PID参数设置为kP=9，kI=10，kD=7.2．设二次网供水温度为40 ℃，开始仿真，使用示波器观察系统输出波形，将传统PID、模糊PID和变论域模糊PID进行对比.

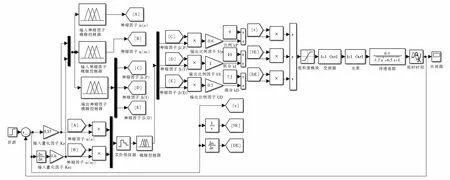
图2 变论域模糊PID仿真Fig.2 Simulation of variable domain fuzzy PID

3.2 变论域模糊PID仿真分析

变论域模糊PID的阶跃响应曲线如图3所示.通过计算上升时间、超调量、调节时间和稳态误差4个参数的对比分析结果见表4.

表4 阶跃响应曲线参数Table 4 Parameters of step response curves

传统PID的上升时间短，超调量大，调节时间过长，稳态误差有较小的震荡，系统响应时间长，在96 s才趋于稳定状态，响应曲线震荡较大；模糊PID上升时间与传统PID相同，超调量减少5.9 %，调节时间减少9 s，稳态误差减少0.1 %，与传统PID相比响应速度加快，稳态误差降低，但超调仍较大，响应曲线震荡较小；变论域模糊PID上升时间相比模糊PID增加1s，超调量减少8.47 %，调节时间减少27 s，稳态误差基本为0，与前两种算法相比响应速度快，超调量小，响应曲线平稳没有震荡，能够快速达到设置温度值，控制精度相对比前两种算法分别提高了0.11 %和0.01 %，实现了温度的精确控制.

当3种控制都趋于系统稳定时，在时间为100 s时，给控制系统温度为5 ℃的干扰，抗干扰阶跃响应曲线如图4所示，当系统受到外界温度干扰时，传统PID有较大幅度震荡，经72 s系统趋于稳定，抗干扰能力差，模糊PID经53 s系统趋于稳定，系统有小幅震荡，抗干扰能力较差；变论域模糊PID经23 s系统趋于稳定，震荡幅度小，曲线较平稳，用最短的时间恢复稳态，具有较强抗干扰能力.

图3 阶跃响应曲线Fig.3 Curves of step response

图4 抗干扰阶跃响应曲线Fig.4 Curves of anti-interference step response

4 结论

针对太阳能供热控制系统中温度控制精度不高、抗干扰能力差、响应速度慢等问题，使用变论域思想结合模糊PID算法，利用输入输出量伸缩因子的收缩和扩大改变系统的模糊论域，设计基于模糊推理选择伸缩因子的变论域模糊PID控制器．利用MATLAB仿真，结果表明变论域模糊PID控制器系统的动态响应增加，系统抗干扰能力增强，系统稳定性提高，提高了系统温度控制精度，有较好的控制性能，提升了系统供热精度和能源的利用率，满足控制系统要求.