基于量子计数的贝叶斯二元分类算法
2021-12-22陆春悦郭躬德
陆春悦,郭躬德,林 崧
(福建师范大学计算机与网络空间安全学院,福建 福州 350117)
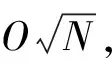
贝叶斯分类算法是一种常见的机器学习算法,它利用贝叶斯定理与联合概率模型进行分类预测,被广泛应用于文本分类. Shao[11]在2020年提出了基于块编码的量子贝叶斯分类算法(简记为Shao算法). 该算法将块编码与贝叶斯分类相结合,实现了指数级加速. 然而,该算法仅仅适用于厄米矩阵. 本文针对这一问题进行研究,提出了一种基于量子计数的贝叶斯二元分类算法. 该算法通过量子计数与相位估计,快速得到能够反映待分类数据属于第k类别概率的相关值,获取待分类数据所属类别. 本文所提算法在低维特征空间中与经典算法相比有着指数级加速,也可应用于更为普遍的数据集.
1 背景知识
1.1 朴素贝叶斯分类算法

(1)
(2)
因此,贝叶斯分类过程要求计算概率,
(3)

(4)
显然,后者是算法的主要步骤.这样,经典贝叶斯分类算法所需的时间复杂度为O(NM2+M2).因此,如何高效地执行该步骤,是提高整个算法效率的关键.在第2节中,本文为该步骤设计了相应的量子算法.与经典贝叶斯二元分类算法相比,该量子算法能够指数级地降低时间复杂度.
1.2 量子计数
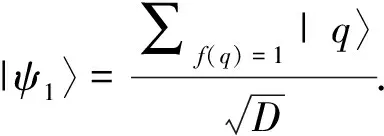
(5)


(6)
进一步,对G算子进行相位估计可得整个系统空间量子态为:
(7)
然后,在计算机上对寄存器|2θ〉进行测量,可以获得θ的估计值,从而得到问题的解的个数D.
2 基于量子计数的贝叶斯二元分类算法
本节所提出的量子贝叶斯二元分类算法,主要分为4个步骤:制备量子初态;量子计数;量子测量得到相关概率;通过后续简单的计算,确定测试样本的类别.整个量子算法电路图如图1所示.
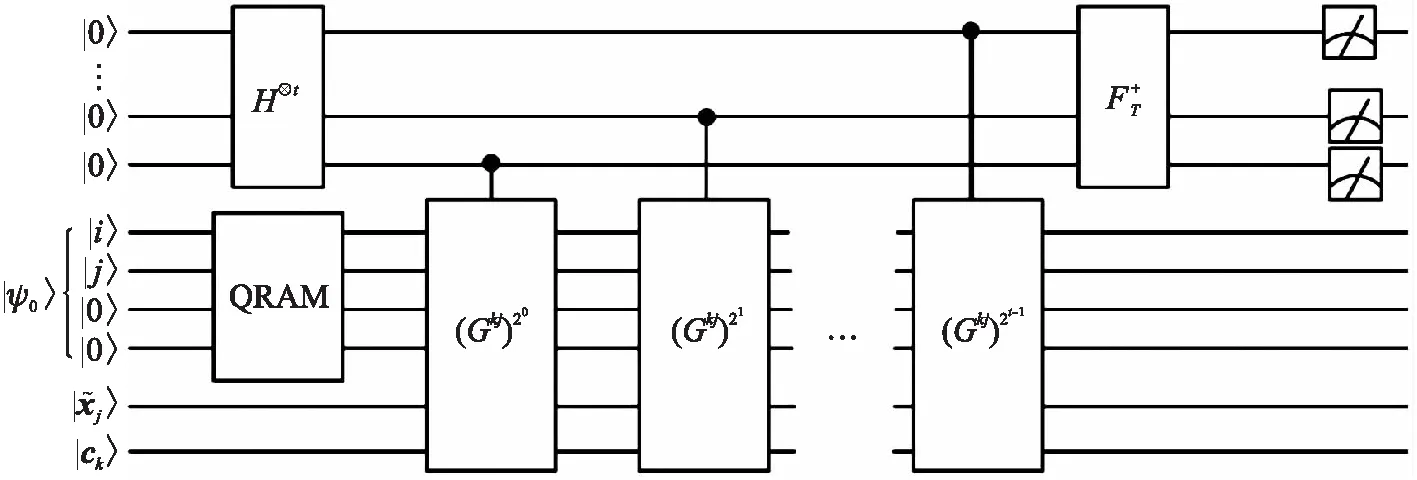
图1 量子贝叶斯二元分类算法的整体量子电路图Fig.1 The overall quantum circuit diagram of quantum Bayesian binary classification algorithm
步骤1:制备量子初态
考虑M维向量,将该经典数据映射到量子态,需要log2M个量子比特来存储该数据.这里,利用量子随机访问存储器[16](quantum random access memory,QRAM)来并行访问数据,并以相干量子叠加方式进行内存访问.假设R是一个地址寄存器,它包含叠加的地址(为叠加地址的振幅),QRAM将返回1个属于该地址寄存器的叠加量子态.如式(8)所示:
∑αφα|α〉R→∑αφα|α〉R|Dα〉dr.
(8)
本算法需要O(logMN)次操作来访问数据,N为训练数据样本数,如式(9)、(10)所示:
(9)
(10)
步骤2:量子计数


图2 量子黑盒电路图Fig.2 The quantum oracle circuit diagram
(11)
此时,便实现了类似于Grover的黑盒操作.
(12)
构造与之对应的Gkj算子,
Gkj=(2|χN〉〈χN|-IN)O,
(13)

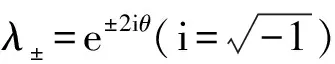
那么,在Gkj算子的本征态空间上重新描述|ψ〉,可得:
(14)
然后借助辅助粒子进行相位估计[3],可得:
(15)
步骤3:投影测量

步骤4:计算类别

3 复杂度分析
这一节中,对上述量子算法的时间复杂度进行简要分析.各步骤的时间复杂度如表1所示.

表1 复杂度分析Table 1 The complexity analysis


4 结论

