基于Fisher判别的接触式轮廓仪自动标注分析

王 军

基于Fisher判别的接触式轮廓仪自动标注分析

王 军

（安徽财贸职业学院公共教学部，安徽 合肥 230601）

针对接触式轮廓仪的自动标注问题，运用Fisher判别法、一元回归分析等方法建立了被测工件在水平状态和倾斜状态下的轮廓线中槽口宽度、圆心间距离、斜线与直线夹角、圆半径等参数值的数学模型，根据平面向量旋转方法对倾斜状态下被测工件轮廓线进行校对和修正，并利用配对T检验法分析2种测量状态下被测工件各项参数计算值之间的差异，完成了不同测量状态下接触式轮廓仪自动标注分析的研究过程。

Fisher判别分析；配对T检验法；回归分析；平面向量旋转

接触式轮廓仪是对物体的轮廓以及二维尺寸和位移进行测量的一种仪器，可以通过将测针从待测物体表面划过的方法来获取以普通方法难以获得的精确参数，传感器在被测物体表面做匀速滑行时，前端触针可感受到物体表面的几何变化，在X和Z方向分别进行采样后经过一系列处理转换成数字信号储存在系统的存储器中，测量结果具有可靠、稳定、重复性好等特点。但因接触式测量需直接与物体表面进行接触，针尖会在被测工件表面留下划痕，容易因接触而造成针尖和工件原始形貌受到磨损，测量误差必定存在。如何判断、校正和修正不同状态下被测工件测量参数以及比较不同状态下被测工件各项参数值之间的差异性成了研究学者讨论的问题。

为此黄富贵等[1]提出了工件边缘轮廓参数的提取与精度评定方法；孙艳玲等[2]提出测量力的数学模型对接触式表面轮廓测量仪测量力做了线性可控研究；孙艳玲等[3]分析了大量接触式轮廓测量过程中非线性误差产生的原因，运用多项式拟合误差补偿算法对接触式表面轮廓测量仪的误差做了分析与补偿；尤越等[4]提出一种基于Matlab的非球面光学元件面形参数的新方法。这些方法更多倾向于测量方法的改进和测量数据的误差分析与补偿，为本研究提供了一定的理论方法支持，但如遇到不同状态下工件海量数据处理和修正方法并未提及。

本文基于2020年全国大学生数学建模D题中给出的不同状态下被测工件测量数据，利用Fisher判别和回归分析，建立了计算被测工件轮廓线中槽口宽度、圆心间距离、斜线与直线夹角、圆半径等参数值的数学模型，利用配对T检验法分析2种测量状态下被测工件各项参数计算值之间的差异，并建立校正模型对其进一步地修正。

1 水平状态下接触式轮廓仪自动标注分析

1.1 数据预处理

为保证计算的准确性，结合水平状态下被测工件的数据，进行数据清洗、噪音过滤，剔除异常数据和缺失性数据，最终以被测工件水平状态下139 985条数据作为有效数据进行问题讨论。

1.2 水平状态下被测工件轮廓线中各项参数值的数学模型与求解

观察被测工件在水平状态下的轮廓线，该轮廓线由24个线段和圆弧构成，为找到线段和圆弧的分界点，采取Fisher判别对水平状态下被测工件的数据进行分类处理，以2类为例，设有A、B 2类观察对象，令A={1,2,…,x}为A类的判断指标，B={1,2,…,x}为B类的判断指标，构造线性组合：

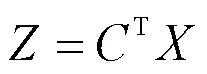
Fisher判别为尽可能地分开样本，使各类类间差异性尽可能大，同时类内离散度尽可能小。为此设判别函数：

其中A、B分别为A、B 2类的样本均值，A、B分别为A、B 2类的离散度矩阵，求出最优投影方向：

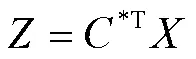
在被测工件轮廓图中各个线段和圆弧中间取部分数据，分别以此为训练集，标为1，2，3，…，24组，在分界点的邻域中的数据不取分组，利用Fisher判别判断分界点的邻域中数据的归类，在Matlab软件中编程求解，得到水平状态下被测工件轮廓线中各分界点分布情况，见表1。

表1 水平状态下被测工件轮廓线中各分界点分布表

序号XZ 146.595892371385-1.77086065 249.881439135836-2.066344119 350.5024262497722-3.765033665 451.9261487608082-3.813180337 552.5194021842234-2.131027001 657.7561856241473-2.13350831 758.2508282865925-3.969414726 859.0627722952317-3.990261059 959.6097363810847-2.187914377 1064.8647403414056-2.268426393 1165.3078362561049-3.93557546 1266.1533282865925-3.949917937 1366.6206612968921-2.316972668 1471.9781288645574-1.73421356 1576.7500221339145-0.787872156 1681.1616396809662-1.645686414 1784.8569115098883-1.878285278 1886.4270229349622-2.030265697 1987.7565452010095-1.552391698 2089.6644048852199-1.775289293 2194.9603541532444-2.628246141 22101.087906430329-2.693894637 23107.172045532044-0.980010892 24113.356269680811-0.894240548 25118.123985877831-1.786456207

根据被测工件分界点数据，将水平状态下被测工件的数据进行拆分，分成24个子表，利用子表数据依次计算被测工件中的各项参数值。

为计算被测工件轮廓图中斜线与水平直线之间的夹角以及水平直线的长度和槽口的宽度，选取24个子表中线段类的数据表，做一元线性回归分析，得到13个线段所对应的直线方程，见表2。

表2 水平状态下被测工件轮廓线中各线段的回归方程表

序号回归方程 1y=-1.434-0.07x 2y=134.782-2.743x 3y=-149.015+2.796x 4y=-1.900+0.02x 5y=212.917-3.723x 6y=-197.026+3.269x 7y=-1.727-0.01x 8y=240.061-3.736x 9y=-235.664+3.503x 10y=-2.445+0.100x 11y=-16.041+0.199x 12y=14.600-0.200x 13y=-2.420-0.180x

计算被测工件轮廓图中2个线段的夹角和线段与水平直线的夹角时，利用表2中的回归方程，例如设两直线的回归方程为：

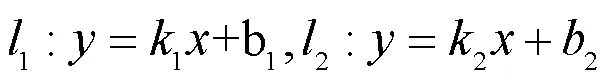
把被测工件轮廓线的各项参数值标在水平状态下被测工件轮廓图中，见图1。

表3 水平状态下被测工件轮廓线中各项参数值分布表

参数指标数值参数指标数值参数指标数值参数指标数值参数指标数值 x12.637963048x83.695271829r10.74391079c17.490733138∠2110.8255455 x25.23678344x91.329522266r20.16526132c26.900376865∠3103.8890537 x31.853550757x105.295949268r30.49282198c320.10204639∠4106.4361396 x45.25500396x116.127552277r40.99361252c42.924792039∠5105.5577963 x51.755920955x126.084139102r51.21045682c59.426842509∠6111.6430267 x65.357467568x136.184224149r64.00874159c612.24750131∠7171.4557633 x79.183510816z0.898814258r73.99345037∠1114.0342253∠8173.8940412

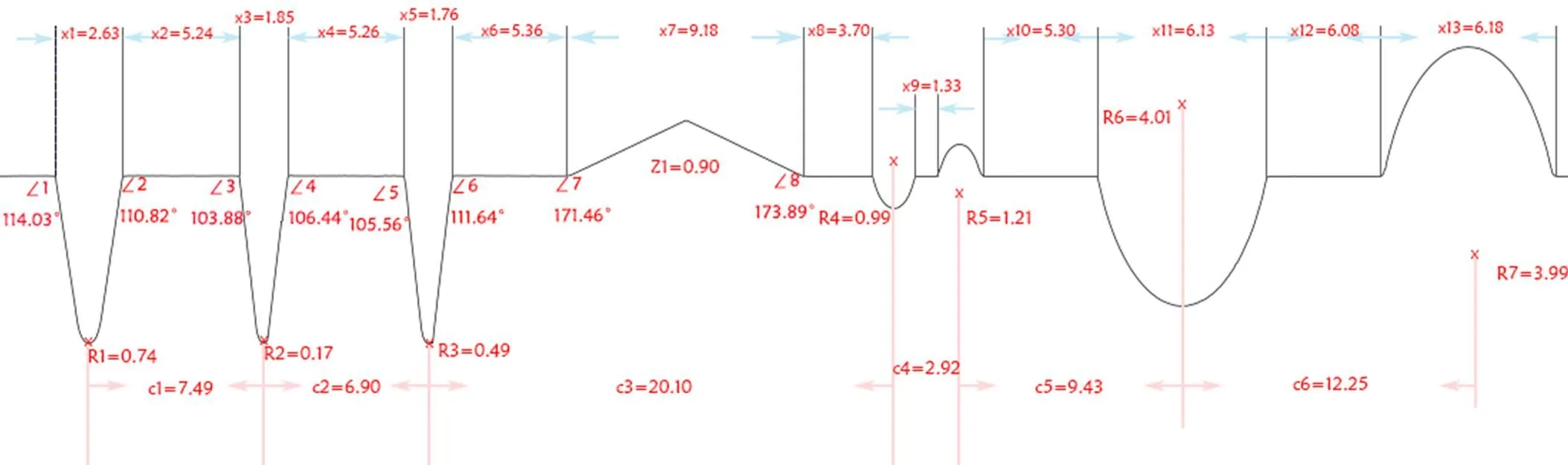
图1 水平状态下被测工件轮廓线中各项参数值分布图

2 倾斜状态下接触式轮廓仪自动标注分析

2.1 倾斜状态下被测工件轮廓线中各项参数值的求解

对倾斜状态下被测工件数据进行处理，剔除无效数据和异常数据，并在此基础上计算该被测工件的倾斜角度和水平位移。对处理后的数据绘图和水平状态下测量的轮廓线相比较，比较水平状态和倾斜状态下被测工件的轮廓线，发现倾斜状态下的轮廓线左端有一定的向上倾斜。

利用1.2中Fisher判别分析原理对倾斜状态下被测工件数据进行各个线段和圆弧的分界点的处理，得到表4。

计算被测工件轮廓线的倾斜角度时，鉴于工件自身属性，不考虑分界点中2点之间的数据，使用分界点的数据计算工件的倾斜角度，以2点为例，假设已知固定点(0,0)，再在2个工件中确定2个相对位置相同的点，分别设为(1,1)，(2,2)。将3个点分别相连，并计算出3条直线的长度：

表4 被测工件在倾斜状态下的线段和圆弧的分界点统计表

序号XZ 148.78316600644051.403380125 252.26921603888960.949647859 352.8819850235423-1.721918776 453.7982450424055-2.0125782 555.14414787702080.53368709 660.1595809522166-0.473671481 760.4046236115269-2.312455991 861.0771158312883-2.983671385 962.1167635978751-0.473207064 1067.0100852131491-0.97688334 1167.4301879273466-3.362005744 1268.1112465329891-3.847416843 1369.1507675174781-1.322296007 1474.1162180177504-1.899586855 1579.1827265227793-1.570421495 1683.9525269257363-3.169843738 1787.0720414333876-3.716071109 1888.8432481227465-3.835922966 1989.8226362320414-3.907635848 2091.5370061277093-4.031136859 2196.61365107078224.991381133 22103.7096786537270-5.861271216 23108.7225209468370-6.374395626 24115.8119452639940-7.10620431 25119.6878441607650-7.865819837

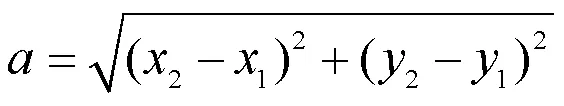
计算被测工件在测量时的平移位移，通过计算被测工件在水平状态和倾斜状态下对应的相应分界点的水平距离差，并求出平均数作为水平移动的位移，得到倾斜状态下被测工件向右平移了=1.9294104980141595。

2.2 倾斜状态下测量工件参数值校正模型的建立与求解

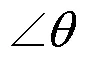
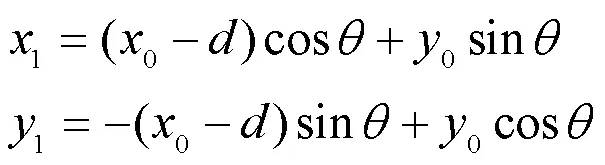
即可求解出校正后点的坐标，利用Matlab软件处理，将未校正被测工件所有点的数据代入计算后即可得出近似水平的结果，再利用1.2中的求解方法，计算出被测工件校正后轮廓线中各项参数值，具体指标数值见表5。

将被测工件校正后轮廓线中各项参数值标识在轮廓线上，见图2。

表5 被测工件校正后轮廓线中各项参数值统计表

参数指标数值参数指标数值参数指标数值参数指标数值参数指标数值 x12.904559199x83.16387859r10.73135887c19.45753671∠2110.2685124 x25.10338938x90.98046948r20.198664611c27.032228467∠3103.9874519 x31.940832011x105.15802552r30.410525473c319.97355677∠4107.5843571 x44.917442518x117.14896601r41.014522923c42.796983412∠5105.3485845 x52.167337829x125.03718485r51.022462746c59.54506568∠6109.3489557 x64.998449302x137.12463898r64.00828736c612.23622337∠7170.5948513 x714.91643697z0.91584585r74.024524599∠1110.1542648∠8169.8549852

图2 被测工件校正后轮廓线中各项参数值分布图

3 不同状态下被测工件轮廓线中各项参数值差异性比较

针对水平状态和倾斜状态下被测工件轮廓线中的各项参数值，采用配对样本T检验法比较2种测量状态下各项参数计算值的差异，得到比较结果，见表6，依据分析结果认为校正后轮廓线的各项参数值和水平状态的参数值有差异，但不明显，所建立的校正模型不失有效性和科学性。

表6 2组数据配对样本T检验结果

配对1平均值标准差标准误差平均值95%的置信区间下限95%的置信区间上限T自由度显著性 水平&校正0.93161.52960.25860.43230.6186360340.729

4 评价与推广

针对接触式轮廓仪的自动标注问题，使用了Fisher判别分析、一元线性回归分析、Matlab软件等对数据进行处理，得到了不同状态下工件的轮廓图各个部分参数值，利用平面向量旋转方法对工件在倾斜状态下的工件进行了校正，用配对T检验法比较了2种测量状态下工件各项参数值的差异，检验了校正模型的有效性和科学性。在模型的改进中可以智能优化算法，比如引入遗传算法和粒子算法去优化模型，这些情况都会影响模型的准确性，这也是所建模型的改进方向。

[1] 黄富贵, 苏建平. 基于图像测量技术的薄壁零件轮廓参数测量方法[J]. 工具技术, 2006, 35(6): 61-63.

[2] 孙艳玲, 常素萍. 接触式表面轮廓测量仪测量力线性可控的研究与实现[J]. 计量学报, 2014, 40(6A): 32-38.

[3] 孙艳玲, 梁煜恒, 常素萍. 接触式表面轮廓测量仪的非线性误差分析与补偿[J]. 计量技术, 2015(5): 10-13.

[4] 尤越, 王乔方, 字正华. 一种基于Matlab的非球面光学元件面形参数测试技术[J]. 红外技术, 2014, 36(4): 331-335.

Automatic Marking Analysis of Contact Profilometer Based on Fisher Discriminant

WANG Jun

（Department of Public Education, Anhui Finance & Trade Vocational College, Hefei 230601, China）

In view of the problem of automatic marking of contact profilometer, the mathematical models of notch width, distance between centers of circles, angle between oblique line and straight line, radius of circle and other parameters in the contour line of measured workpiece in horizontal and inclined state are established by using Fisher discriminant method and one variable regression analysis. The contour line of workpiece under inclined state is calibrated according to plane vector rotation method. In addition, the paired T-test method is used to analyze the difference between the calculated values of various parameters of the workpiece in the two measurement conditions, The research process of automatic annotation and analysis of contact profilometer in different measurement states is completed.

Fisher discriminant analysis; paired T-test; regression analysis; plane vector rotation

10.15916/j.issn1674-3261.2021.06.004

F724.2

A

1674-3261(2021)06-0368-05

2020-11-06

安徽高校自然科学研究项目(KJ2019A1203)；安徽高校自然科学研究项目(KJ2019A1205)；安徽省高校优秀青年人才支持计划项目(gxyq2020144)

王军(1981-)，男，安徽淮北人，副教授，硕士。

责任编辑：孙 林