考虑偏载啮合的齿轮系统接触分析及其啮合刚度求解

许月强，张 昊

考虑偏载啮合的齿轮系统接触分析及其啮合刚度求解

许月强，张 昊

（辽宁工业大学 机械工程与自动化学院，辽宁 锦州 121001）

齿轮运转过程中发生偏载是引起齿轮转子系统异常振动的原因之一，有限元法能够较为准确地模拟齿轮偏载啮合过程，进而通过接触面应力状态分析其偏载带来的影响。为了研究偏载对于齿轮啮合接触力及其齿轮啮合刚度的影响，基于SolidWorks参数曲线方程建模，联合运用Hypermesh和AnsysWorkbench对模型有限元仿真，得到了不同偏载角度下啮合齿轮接触面应力分布及其时变啮合刚度变化曲线。结果表明，齿轮偏载作用下，接触形态随偏载角度加大更多地偏向于角接触，接触面积逐步减小；接触应力集中，接触应力最大值与均值在不同偏载状态下数值不同，整体逐渐增大；实际啮合刚度与理论啮合刚度曲线基本吻合，有限元法更贴合实际；接触刚度随偏载角度增加，整体刚度曲线升高。

齿轮偏载；有限元仿真；接触应力；时变啮合刚度

齿轮偏载表现为直接改变齿轮接触状态，接触状态变化进而导致齿轮工作性能的改变。在实际啮合过程中，总会存在因安装误差或运转失配等导致的齿轮啮合偏载。时变啮合刚度是研究齿轮接触区域应力变化必不可少的内部参数激励之一，是齿轮动力学研究的理论基础。因此研究齿轮偏载下齿轮传动动力学响应及其时变啮合刚度求解，对于转子机械具有很强的工程实际意义。

关于齿轮接触状态分析和时变啮合刚度求解，国内外许多学者或基于弹性材料力学、或基于有限元法对其进行了大量研究。如Lias等[1]研究了齿面接触偏差下啮合力变化曲线，接触面积状态变化，提出接触偏差越大应力越大，接触面积呈现“笋形”分布。Jiang等[2]建立了8自由度的啮合失配齿缺陷螺旋齿轮副模型，通过对不同摩擦系数模型和啮合副失配的螺旋齿轮副实例的仿真，得到了啮合刚度沿接触线的变化规律，提出了一种改进计算时变摩擦力和动态啮合力的计算方法。Hassan[3]在其最近的研究中使用叠加模态法对三段齿轮齿的二维有限元模型进行了仿真分析，推导计算了直齿圆柱齿轮的瞬态应力，利用Lanczos提出的块体固有频率模型确定了齿根处的应力分布。Saxena等[4]运用势能法，开发了一种研究轴向偏差和滑动摩擦对齿轮时变啮合刚度影响的有限元仿真程序，探究考虑滑动摩擦的正齿轮啮合失配运动特性。何育民等[5-6]采用准静态法求解了齿轮啮合刚度，同时还研究了不同重合度对齿轮综合啮合刚度影响，揭示了理论啮合刚度与实际啮合刚度不同步现象。李添翼等[7]通过有限元仿真和试验台实验对比，求解齿轮啮合刚度，对比得出有限元法模拟是最贴近真实工况的方法。白恩军等[8]基于有限差分法，分析研究了齿轮轴变形下一对斜齿轮传动系统接触特性，观察其载荷分布情况。王涛等[9]提出一种动态啮合刚度计算方法，给出了转速对于动态啮合刚度影响，转速不同，动态啮合刚度不同。蒋建政等[10]提出3种不同啮合刚度直齿圆柱齿轮计算模型，研究了3种模型在高速、低速2种工况下的啮合力和传递误差动态变化规律。

本文针对多点啮合转子实验平台齿轮系统，基于参数曲线方程建立一对不同偏载角度下的直齿圆柱齿轮啮合模型，采用Hypermesh划分网格，通过ANSYS workbench接口导入分好的网格进行静态动力学计算，得到其啮合接触应力沿齿宽方向的分布状态以及动态啮合刚度曲线，以此来分析齿轮偏载作用对齿面啮合接触应力和时变啮合刚度曲线的影响。

1 齿轮偏载动力学建模

1.1 参数化建模

模型选取实验用多点啮合齿轮轴承转子系统多物理场监测平台的一对输入齿轮和输出齿轮，基于实验相似原理，按比例建立的实体单元模型。借助Solidworks参数曲线方程建模工具，建立装配了不同轴向偏载角度下精确的直齿啮合齿轮副三维有限元模型，齿轮相关具体参数如表1所示。

表1 齿轮副参数

齿轮副主动轮从动轮 模数1010 齿数3026 压力角2020 齿宽3030 轴孔直径4040 变位系数0 中心距280 重合度1.7423

参数曲线方程为：

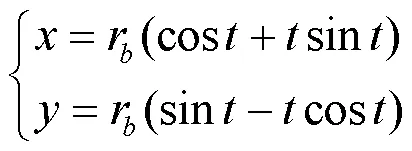
式中：r表示基圆半径，∈[0，π/2]。

图1 轴向偏载三维建模

1.2 网格划分

Hypermesh网格划分，基于2D网格到3D网格映射的方法，其中2D网格单元采用2∶1型网格过渡，单元采用六面体单元，单元尺寸0.5 mm。最终生成全局网格如图2(a)所示，模型共划分150 592单元，165 378节点。为保证齿面接触精度和求解精度，减少仿真计算时间，将齿轮分为轮毂部分和轮齿部分两部分，轮毂部分采用疏化划分，轮齿部分局部网格加密。轮齿加密网格如图2(b)所示。

图2 网格划分

1.3 有限元求解

首先，将齿轮副网格模型通过Workbench的Finite Element Modeler有限元网格模块导入，再次，建立静力学模块，使之两者Model模块模型互联共享。在工程属性模块下，赋予齿轮副材料属性，材料类型见表2所示。

表2 材料类型

材料密度/(kg·m-3)弹性模量/GPa泊松比μ Steel78502×10110.3

在主动轮轴心处添加大小为电机额定输出转矩的扭矩=70 N·m，从动轮轴孔处施加固定约束。约束定义与载荷加载如图3所示。

图3 约束与载荷

2 齿轮啮合接触应力分析

齿轮啮合时，轮齿间啮合接触力，沿主动轮和从动轮间的啮合线传递[12]。如图4所示，垂直于啮合接触面的力F存在两个分力，即切向分力F和径向分力F。

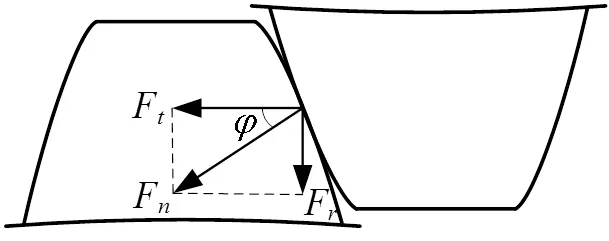
图4 啮合接触力

从图4中可知：

定义局部坐标系，齿轮轴线方向为坐标系的Y轴，齿轮径向为坐标系的X轴。仿真结束后提取啮合接触面区域，实际参与啮合的节点应力值及其位移，绘制了非偏载和偏载状况下接触应力t沿齿宽

方向随位移变化等高曲线，如图5所示。

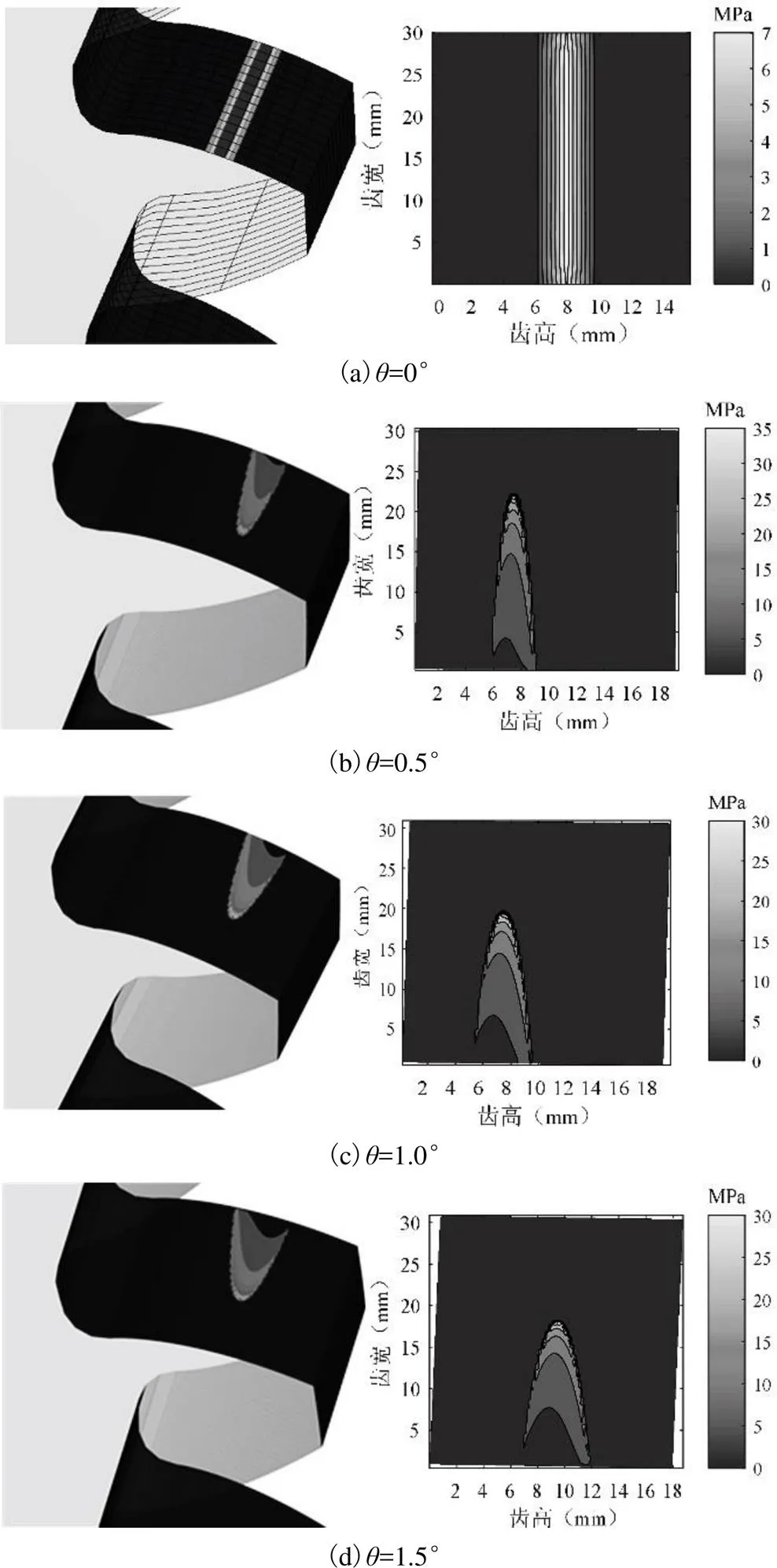
图5 接触应力-位移变化

由图5可见：应力沿齿宽方向（Y方向）和齿轮径向（X方向）分布情况，以及各偏载角度下实际接触面积分布变化。随着偏载角度增大，可见接触应力集中于角接触点上，此时该点应力值最大，最大值位置沿齿宽向齿端一侧变动；接触应力在无偏载状态下沿齿宽呈现均匀分布；在偏载状态下，应力分布不均匀，从开始啮合时的两齿轮角接触点处应力最大，向齿端边缘逐渐减小，于齿端一侧的齿腹边缘处消失，并且偏载角度越大，齿宽方向应力分布的长度越短；同时，图中的colorbar显示偏载作用下的应力最大值比无偏载作用下的应力最大值增大4倍左右。实际接触面积的变化显示：在无偏载状态下，接触形态沿齿宽呈现条形分布，偏载状态下沿齿宽呈现近似“笋形”分布，并且接触面积随偏载角度增大而减小。此外，在每张偏载角度下的应力-位移图齿高方向两侧，均出现了微小的白色三角形区域，该区域在齿宽方向所呈现的最小锐角恰好等于各自的偏载角度。

啮合等效应力通常可用接触面法向载荷因子来反映，具体接触区域的齿面和齿根处载荷因子计算公式如式(3)、式(4)所示。

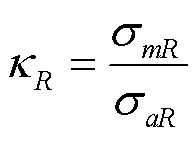
提取齿根齿面等效应力，根据式(3)、式(4)绘制了不同偏载角度下接触载荷因子变化曲线如图6所示。由图6可见，不同偏载角度下的载荷因子，无论是齿面载荷因子值，还是齿根载荷因子值都明显高于无偏载状态相应载荷因子值，且随偏载角度的增大，齿面载荷因子值不断增大，齿根载荷因子值趋势增大。这反映了应力均值随偏载角度增大而增大，结果或将加剧齿轮啮合运转时异常振动，长时间运转可能加快齿轮疲劳断裂。

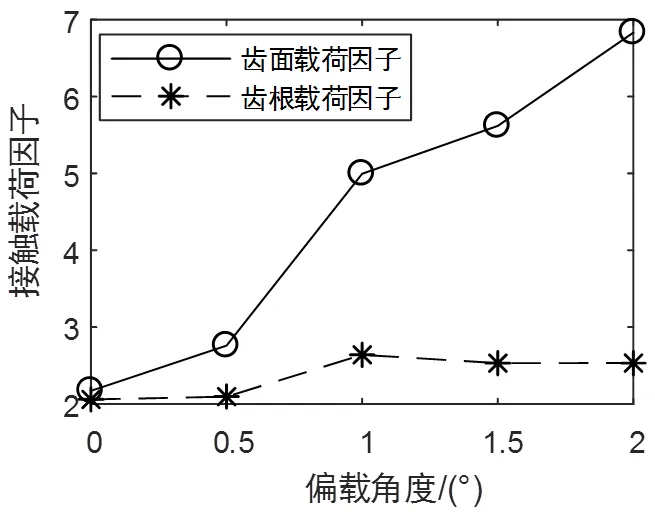
图6 接触载荷因子随偏载角度变化曲线

图7给出了有限元仿真结果拿到的实际啮合接触齿宽、啮合面压力最大值与偏载角度的关系。由图7可见，随偏载角度增大，实际接触齿宽宽度'，在偏载0°～1.5°内，由原来无偏载下的实际接触齿宽30 mm减小到偏载1.5°后的17 mm；同时，随着一定限制内的偏载角度的逐渐加大，啮合面上的接触应力最大值逐渐加大，具体数值由438.5 N增大到589.8 N。

3 动态啮合刚度求解

3.1 动态啮合刚度计算

有限元法将单齿啮合刚度直接定义为轮齿啮合线上发生单位挠度变形所需的载荷值[13]，如式(5)所示。

图7 不同偏载接触应力沿齿宽分布

式中：F为齿面接触力的法向分力，为单齿综合弹性变形。

齿面接触力可近似由电机扭矩和齿轮基圆半径计算，如式(6)所示。

单齿综合弹性变形，包括轮齿弯曲变形位移δ和局部赫兹接触变形δ。多对轮齿参与啮合时，出现单齿啮合区和双齿啮合区交替变化，并在双齿啮合区发生刚度耦合效应[14]，故一对啮合齿轮的轮齿综合弹性变形计算如式(7)所示。

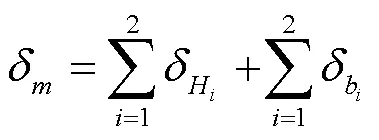
综上，有限元法下的齿轮时变综合啮合刚度计算如式（8）所示。

式中：为同时发生啮合时最大啮合齿数。

石川公式[15]将轮齿简化为一个由梯形与矩形组成的悬臂梁，啮合过程中，单齿所受的载荷引起的啮合线方向综合弹性变形量计算用式(9)表示。

式中：12为沿啮合线方向的综合弹性变形量，δ为矩形部分的弯曲变形量，δ为梯形部分的弯曲变形量，δ为剪切变形量，δ为基体倾斜变形量。

故石川法下的齿轮时变综合啮合刚度计算如式(10)所示。

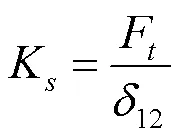
3.2 时变啮合刚度对比分析

提取啮合节面上发生的位移，该位移为某时刻综合接触变形值，根据公式(5)～(10)，计算出有限元仿真下的不同偏载角度的啮合刚度曲线。

如图8所示为无偏载状态下采用有限元法和石川公式法得到的啮合刚度对比图。由图8可见：有限元法计算得到的刚度曲线的单齿啮合区刚度值，高于相应位置的由石川公式计算得到的刚度值；两种方法所得的最大刚度值差别不大。

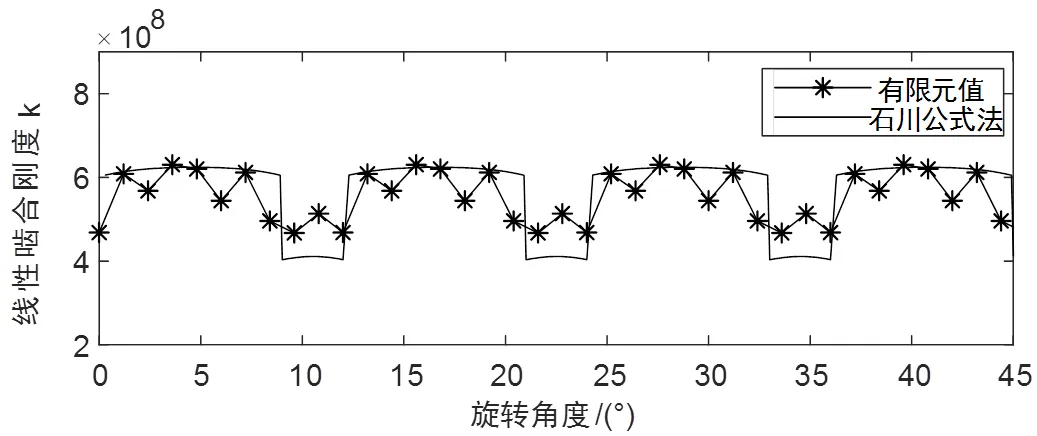
图8 时变综合啮合刚度对比

将上述2种方法与ISO标准[16]作相对误差比较，如表3所示。由表3可见，通过啮合刚度对比及其误差比较，发现有限元法所得到时变啮合刚度平均值相比石川法所得结果的误差更大，且误差比较更加贴近ISO标准。

表3 啮合刚度误差比较

ISO有限元法石川公式法 时变啮合刚度平均值5.9707e+08 N/m5.5295e+08 N/m5.1370e+08 N/m 与ISO标准相对误差—7.39%13.96%

针对齿轮偏载，基于同样的动态啮合刚度计算提取方法，仿真得到不同偏载角度下的时变啮合刚度曲线，如图9所示。由图9可见：随着偏载角度的不断增大，整体刚度曲线升高，同时出现单齿啮合区宽度增宽，双齿啮合区宽度减小现象。对曲线进一步处理得到不同偏载角度下最小啮合刚度、最大啮合刚度和平均啮合刚度，如表4所示。由表4可见，3种啮合刚度值随偏载角度增大，不断增大。

图9 不同偏载的时变啮合刚度

表4 不同偏载下各啮合刚度值比较

偏载角度/(°)最小啮合刚度（N·m-1）最大啮合刚度（N·m-1）平均啮合刚度（N·m-1） 0°4.683e+86.306e+85.5295e+08 0.5°4.736e+86.431e+85.6603e+08 1.0°5.103e+86.589e+85.7497e+08 1.5°5.153e+86.958e+85.9828e+08

4 结论

(2)基于有限元法，利用ANSYS Workbench静力学分析模块，模拟仿真分析得到的齿轮啮合刚度值更加贴近工况实际。

(3)通过对不同偏载角度下，齿轮啮合时变啮合刚度变化曲线分析得到，齿轮偏载会带来时变综合啮合刚度值的增加，造成啮合刚度曲线升高；同时，随偏载角度的增加，出现单齿啮合区域宽度增加，双齿啮合区宽度减小。

[1] Lias M R, Rao T V, Awang M, et al. The stress distribution of gear tooth due to axial misalignment condition[J]. Journal of Applied Sciences, 2012, 12(23): 2404-2410.

[2] Jiang H, Shao Y, Mechefske C K, et al. The influence of mesh misalignment on the dynamic characteristics of helical gears including sliding friction[J]. Journal of Mechanical Science and Technology, 2015, 29(11): 4563-4573.

[3] Hassan A R. Transient stress analysis on medium modules spur gear by using mode super position technique[J]. Eng Technol, 2010, 4: 204-211.

[4] Ankur Saxena, Anand Parey, ManojChouksey. Dynamic Analysis of Multi-mesh Geared Rotor System Using Modal Analysis[C]. 2016 Prognostics and System Health Management Conference. IEEE, 2016.

[5] 何育民, 郝安帮. 基于ANSYS workbench齿轮啮合刚度计算及动力学仿真[J]. 沈阳工业大学学报, 2020, 42(2): 191-196.

[6] 何育民, 郝安帮. 实际重合度对啮合刚度及齿轮动态响应影响研究[J]. 机械传动, 2018, 42(11): 52-57.

[7] 李添翼, 武志斐, 王铁, 等. 基于Workbench的齿轮啮合振动分析[J]. 科学技术与工程, 2017(24): 54-59.

[8] 白恩军, 谢里阳, 佟安时, 等. 考虑齿轮轴变形的斜齿轮接触分析[J]. 兵工学报, 2015, 36(10): 1975-1981.

[9] 王涛, 唐增宝. 齿轮传动的动态啮合刚度[J]. 华中理工大学学报, 1992, 20(3): 39-44.

[10] 蒋建政, 陈再刚, 翟婉明, 等. 基于不同啮合刚度计算模型的直齿圆柱齿轮传动系统动力学特性研究[J]. 中国科学: 技术科学, 2018, 48(8): 57-65.

[11] 中华人民共和国国家质量监督检验检疫总局, 中国国家标准化管理委员会. 圆柱齿轮检验实施规范: 第3部分 齿轮坯、轴中心距和轴线平行度的检验: GB/Z 18620.3-2008[S]. 北京: 中国标准出版社, 2008.

[12] Ameen A H. Effect of shaft misalignment on the stresses distribution of spur gears[J]. Eng. & Tech. Journal, 2010, 28(7): 1321-1339.

[13] 朱孝录, 鄂中凯. 齿轮承载能力分析[M]. 北京: 高等教育出版社, 1992.

[14] 李安民. 齿轮传动时变啮合刚度计算及其动态特性仿真分析[D]. 郑州: 郑州大学, 2019.

[15] 韩清凯, 翟敬宇, 张昊. 机械动力学与震动基础及其数字仿真方法[M]. 武汉: 武汉理工大学出版社, 2016.

[16] 成大先. 机械设计手册[M]. 6版. 北京: 化学工业出版社, 2016: 15-107.

Contact Analysis of Gear System Considering Mesh Misalignment and Its Meshing Rigidity Solution

XU Yue-qiang, ZHANG Hao

（College of Mechanical Engineering and Automation, Liaoning University of Technology, Jinzhou 121001, China）

Misalignment occurring during gear operation is one of the causes of abnormal vibration of gear rotor system. The finite element method can accurately simulate the meshing process of gear with misalignment, and then the influence of misalignment through the stress state of contact surface is analyzed. In order to study the influence of misalignment on the gear meshing contact force and gear meshing stiffness, this paper based on Solid Works parametric curve equation modeling, is combined with Hyper mesh and AnsysWorkbench to simulate the model by finite element method. The stress distribution of the contact surface of the meshing gear and the variation curve of the meshing stiffness under different misalignment angles were obtained. The results show that the contact morphology tends to angular contact more with the increase of misalignment Angle, and the contact area decreases gradually. The contact stress is concentrated, and the maximum value of the contact stress is different from the mean value under different misalignment conditions, and the whole contact stress increases gradually. The actual meshing stiffness curve is basically consistent with the theoretical meshing stiffness curve, and the finite element method is more consistent with the actual meshing stiffness curve. The overall stiffness curve increases with the increase of misalignment Angle.

gear misalignment; finite element simulation; contact stress; time-varying mesh stiffness

10.15916/j.issn1674-3261.2021.06.002

TH132.4

A

1674-3261(2021)06-0357-05

2021-01-17

国家自然科学基金项目(51705064)

许月强(1994-)，男，河北石家庄人，硕士生。

张 昊(1985-)，男，辽宁葫芦岛人，副教授，博士。

责任编辑：陈 明