基于矢量拟合的主从控制微电网稳定性分析
2021-12-20王蓉殷彪高阳刘彬王杨宋子宏
王蓉,殷彪,高阳,刘彬,王杨,宋子宏
(1. 国网四川省电力有限公司技能培训中心,四川省成都市 610072;2. 四川大学电气工程学院,四川省成都市 610065)
0 引言
中国提出了到2060 年实现“碳中和”的战略目标,这将极大推动可再生能源技术的发展,以风能、太阳能为代表的分布式电源(distributed energy resource, DER)在现代电力系统中的占比将持续上升[1-2]。同时,传统集中式供电网络的缺点也逐渐凸显。与长距离输配电的传统电源相比,DER 在一定程度上更适合分散的电力需求和资源分配。而含有DER、储能单元和负载的微电网作为传统大电网的重要补充,对利用和发展可再生能源、提高供电可靠性具有重要意义。
然而,微电网在促进节能减排、提高供电可靠性的同时也给电力系统的安全稳定运行带来了挑战。近年来,微网示范工程出现了严重的谐波共振现象和逆变器无故障跳闸事故[3]。因此亟需对微电网稳定分析方法开展相关研究。目前常用的定量分析方法可归纳为基于状态空间模型的特征值分析法[4-9]和基于阻抗的稳定性分析法[10-13]。文献[4]通过建立准确的状态空间模型研究了系统参数与振荡模态之间的关系;文献[10]基于导纳模型分析研究了微电网的稳定性。然而,上述研究主要针对下垂控制的微电网,对主从控制的微电网还缺乏深入的研究。此外,考虑到DER的控制结构和参数是厂家重要的知识产权,一般情况下难以获取其技术细节,基于上述方法的稳定性分析就难以实施。
针对上述问题,本文利用量测阻抗对主从控制微电网的稳定性进行了分析,提出了基于矢量拟合法的微电网稳定分析方法。为提高微电网稳定性,提出了DER 控制参数优化设计方法及在DER 电流环中加入阻尼控制器的微电网阻尼控制方法。
1 基于矢量拟合法的稳定分析方法
1.1 基于主从控制的微电网
微电网是指由分布式电源、负荷、能量转换装置、保护控制装置等组成的能量自治系统。通过闭合/断开并网开关,微电网可以在并网和孤岛两种模式下运行。根据各分布式电源所发挥的作用不同,微电网控制模式可以分为主从控制、对等控制等。本文主要讨论基于主从控制的微电网,其典型结构如图1 所示。

图1 基于主从控制的微电网典型结构Fig. 1 Typical structure of master-slave-control microgrid
所谓主从控制是指微电网以某一DER 为主电源,在孤岛运行时采用V/f 控制为微电网提供电压和频率参考。在并网模式下,微电网通过公共耦合点(point of common coupling, PCC)与主网相连进行能量交互。此时微电网的电压和频率由主网支撑,所有DER 均采用恒功率PQ 控制。在孤岛模式下,微电网与主网断开连接,主电源采用V/f 控制以支撑微电网的电压、频率,从电源仍采用PQ 控制,主、从电源共同为本地负荷供电。PQ、V/f 控制结构图见附录A 图A1。
1.2 矢量拟合法
目前常用的稳定性分析方法有Nyquist 图[14]、基于状态空间模型以及阻抗模型的稳定性分析方法。Nyquist 图只能提供系统是否稳定的定性判断。基于状态空间、阻抗模型的稳定性分析方法因可以对系统稳定性进行定量分析而得到广泛应用。但是,基于状态空间和阻抗模型的稳定性分析方法需要建立系统的精细化模型,而DER 模型的控制结构和参数等详细信息难以获取,便无法建立系统精细化模型用以稳定性分析。为此本文提出了一种基于矢量拟合的稳定性分析方法,无需DER 模型详细参数即可定量分析系统的稳定性。该方法将DER 视为黑盒模型,通过注入扰动测量其阻抗[15-17],基本思路是:在DER 稳态工作点叠加频率为f的小信号扰动电压会激发对应响应电流,通过傅里叶变换、对称分量法处理所得扰动电压与响应电流之间的比值即为DER 在频率f下的阻抗。在获取DER 量测阻抗的基础上根据系统拓扑结构、线路参数等已知信息即可计算系统的聚合阻抗。而系统的稳定性取决于系统聚合阻抗,通过计算聚合阻抗的零点,就可以得到系统的振荡模态,包括振荡阻尼和振荡频率[18-20]。
要计算聚合阻抗的零点首先要将离散的量测数据拟合为频域函数。目前已有学者提出了矢量拟合[21]、矩阵束[22]、Loewner 矩阵[23]等拟合技术。其中矢量拟合法应用更为广泛,因此本文选用矢量拟合法进行微电网稳定性分析。
矢量拟合旨在通过离散的测量阻抗数据确定与之相匹配的频域离散函数f(s):

式中:ak、bk分别为f(s)的留数、极点;c、d为实系数。设置一组初始极点bk0并构建辅助函数α(s):


式中:a、b、c通过α(s)计算求得,具体公式请参见文献[24]。
由式(10)可知,等式两端初始极点bk0相互抵消,zk0成为新的极点,重复上述过程直到收敛,即可求得极点bk。进一步地,可通过如式(4)所示最小二乘法得到c、d,其中Bk和式(7)相同,Ak和x变为:
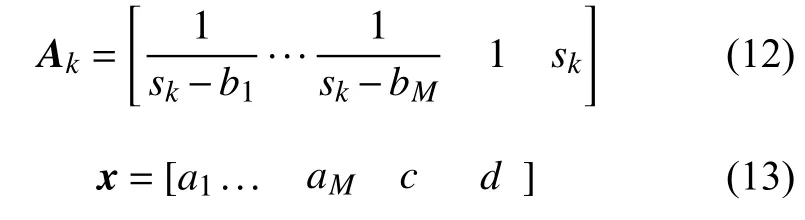
通过上述方法即可获得系统聚合阻抗表达式。
1.3 基于矢量拟合法分析稳定性的步骤
基于矢量拟合的稳定性定量分析方法步骤如下。
步骤1:通过注入扰动测量DER 等黑盒模型的频率响应。
步骤2:根据系统拓扑结构建立微电网阻抗网络模型,计算系统的聚合阻抗Ztotal。
步骤3:对Ztotal使用矢量拟合技术后求解零点,理论上可以得到拟合范围内的所有振荡模态。
2 算例分析
本文在MATLAB/Simulink 平台上建立了基于主从控制的微电网仿真测试模型,该模型包括一个主电源(DER 1)和两个从电源。微电网测试模型如图2 所示。系统额定电压为380 V,额定功率为100 kVA,额定频率为60 Hz。线路参数:R/X为0.5292/0.084。PQ、V/f 控制参数如表1 所示。
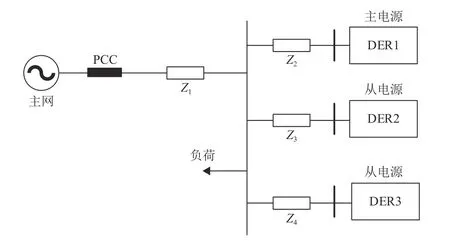
图2 微电网测试模型Fig. 2 Microgrid test model

表1 PQ、V/f 控制参数Table 1 Parameters of PQ and V/f control
2.1 并网模式下微电网稳定性分析
并网模式下,所有DER 均采用PQ 控制,控制参数如表2 所示。负荷阻抗为3.5 Ω。
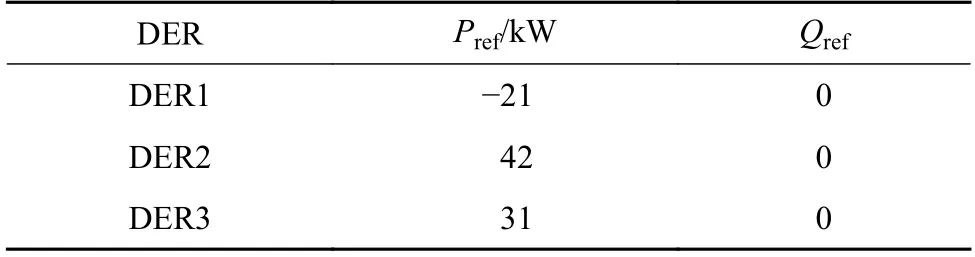
表2 并网模式下的DER 控制参数Table 2 Control parameters of each DER under gridconnected mode
2.1.1 稳定性分析
本文通过改变线路参数分析了微电网稳定性。在3 s 时将线路阻抗Z1由0 Ω 增大至(0.0378+j1.8850) Ω 触发振荡,振荡电流波形见附录A 图A2。利用矢量拟合法求得系统聚合阻抗零点,在右半平面存在一对共轭零点(λ1,2=1.8337±j616.52),表明系统是不稳定的。对应振荡频率和阻尼分别为:98 Hz、−1.83 s−1,与时域仿真结果相吻合。
为了进一步验证算法有效性,本文建立了系统状态空间模型,求得系统聚合阻抗在d-q坐标系下的零点见附录A 图A3,在右半平面存在一对共轭零点(λ1,2=1.79±j240.30),表明系统是不稳定的。对应在abc 坐标系下系统振荡频率和阻尼分别为:98 Hz、−1.79 s−1,与本文算法结果相近,验证了本文算法的有效性。
2.1.2 线路参数对微电网稳定性的影响
本文通过改变Z1探究了线路参数对微电网稳定性的影响:保持Z1电阻R=0.0378 Ω 不变,将电感从1.0 mH 增大至6.0 mH,变化步长为0.1 mH。图3 给出了微电网聚合阻抗主导零点随线路参数的变化情况。本文所有聚合阻抗零点示意图中,红色表示主导零点位于复平面右半平面,蓝色表示主导零点位于复平面左半平面。

图3 系统聚合阻抗主导零点随线路参数变化情况Fig. 3 Variation of dominant zeros of system aggregation impedance with line parameters
2.2 孤岛模式下微电网稳定性分析
孤岛模式下,主电源采用V/f 控制为微电网提供电压和频率支撑,其余从电源均采用PQ 控制,从电源控制参数如表3 所示。
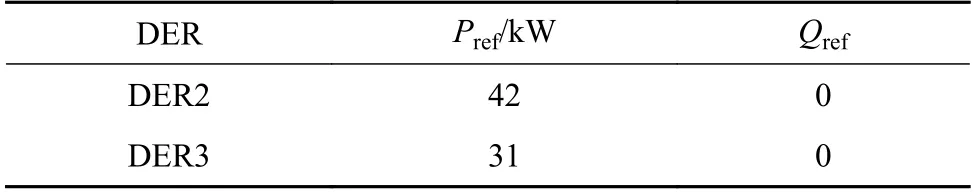
表3 孤岛模式下的DER 控制参数Table 3 Control parameters of each DER under isolated mode
2.2.1 稳定性分析
本文通过改变负荷参数分析了孤岛模式下微电网稳定性。保持负荷电阻R=2 Ω 不变,在3 s时将负荷电感由4 mH 增大至7.5 mH 触发振荡,振荡电流波形见附录A 图A4。
利用矢量拟合法求得系统聚合阻抗表达式,进而求得聚合阻抗零点,在右半平面存在一对共轭零点(λ1,2=20.6±j594.09)表明系统是不稳定的。对应振荡频率和阻尼分别为:94.6 Hz、−20.6 s−1,与时域仿真结果一致。
为了进一步验证算法有效性,本文建立了系统状态空间模型,求得系统聚合阻抗在d-q坐标系下的零点见附录A 图A5,在右半平面存在一对共轭零点(λ1,2=19.63±j217.94),表明系统是不稳定的。对应在abc 坐标系下系统振荡频率和阻尼分别为:94.6 Hz、−19.63 s−1,与本文算法结果相近,验证了本文算法的有效性。
2.2.2 负荷参数对微电网稳定性的影响
本文通过改变负荷参数探究了负荷对微电网稳定性的影响:保持负荷电感L=6.69 mH,将负荷电阻从1 Ω 增大至10 Ω,变化步长为1 Ω,微电网聚合阻抗主导零点随负荷参数的变化情况如图4 所示。

图4 系统聚合阻抗主导零点随负荷参数变化情况Fig. 4 Variation of dominant zeros of system aggregation impedance with line parameters
可以看出,随着负荷电阻增大,系统主导零点逐渐移动到左半平面,能够保持稳定。为进一步验证上述结论,在t=2 s 时,将负荷电阻从4 Ω减小至3 Ω,电流波形见附录A 图A6。时域仿真结果与本文算法结果一致,验证了结论的有效性。
2.3 微电网稳定性控制方法
2.3.1 DER 控制参数优化设计
以2.1.1 节中并网运行模式下因线路参数发生变化使得系统出现的振荡失稳现象为例,通过改变电流环控制参数探究了电流环参数对微电网稳定性的影响:分析比例系数P的影响时,保持积分系数I为30 不变,将P从0.1 增大至1.1,变化步长为0.2;分析比例系数I的影响时,保持积分系数P为0.1 不变,将I 从10 增大至35,变化步长为5。不同控制参数下系统聚合阻抗主导零点如图5 所示。
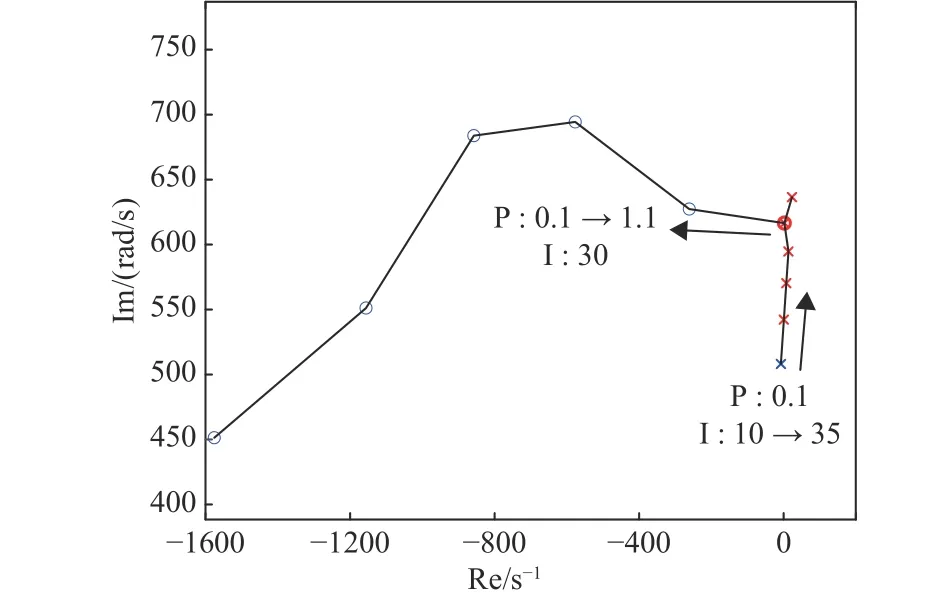
图5 系统聚合阻抗主导零点随控制参数变化情况Fig. 5 Variation of dominant zeros of system aggregation impedance with line parameters
可见,DER 输出阻抗及微电网稳定性受DER控制参数影响。可以通过矢量拟合法求得不同控制参数下系统阻抗主导零点,进而选择使主导零点位于复平面左半平面的控制参数以保证系统稳定运行。例如,将2.1.1 节中DER 电流环Kp参数由0.1 改变为0.3,3 s 时线路阻抗Z1由0 Ω 增大至(0.0378+j1.8850) Ω,微电网仍能稳定运行,微电网仿真电流波形见附录A 图A7。与附录A 图A2相比,控制参数优化后微电网稳定性更优。
2.3.2 附加阻尼控制器
由2.1—2.2 节的分析可知,当线路阻抗、本地负荷等参数发生变化时,系统可能出现振荡失稳现象。为此,可如图6 所示在DER 电流环中加入基于带阻滤波器(band-stop filter, BSF)、带通滤波器(band-pass filter, BPF)、高通滤波器(high-pass filter, HPF)及比例微分(proportion differentiation,PD)控制的阻尼控制器(damping controller, DC)抑制上述振荡现象的发生[25]。

图6 附加阻尼控制器的电流环控制结构Fig. 6 Current loop control structure of supplementary damping controller
本文以2.2.1 节中孤岛运行模式下因本地负荷参数发生变化使得系统出现的振荡失稳现象为例,通过保持DER 初始控制结构、负荷电阻(R=2 Ω)不变,在3 s 时将负荷电感由4 mH 增大至7.5 mH触发振荡,3.2 s 时在电流环中加入阻尼控制器,验证了阻尼控制器的有效性。微电网电流波形如图7 所示。本例中PD 控制参数设置为P=0.1、D=0.001。
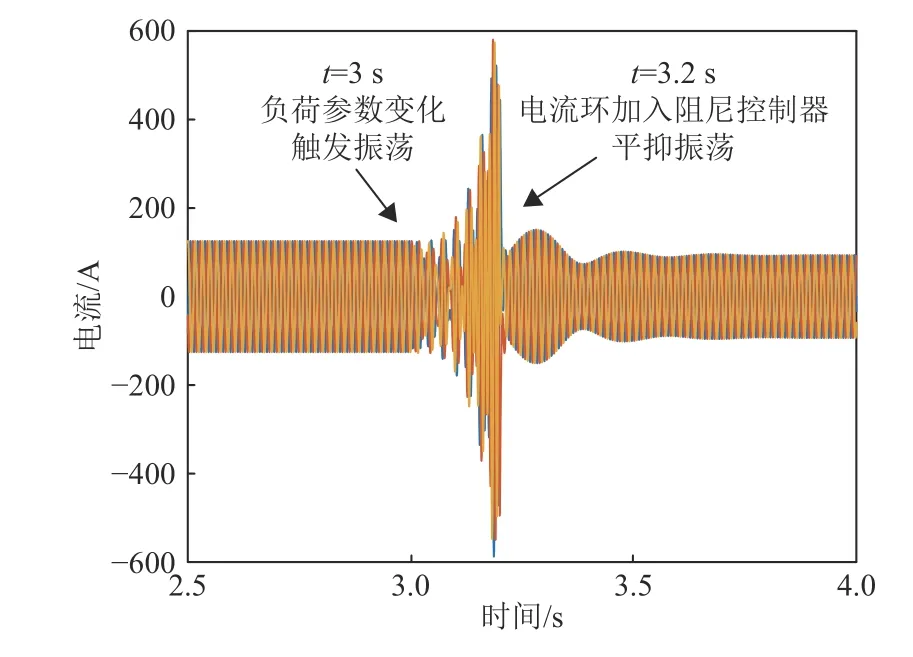
图7 微电网电流波形Fig. 7 Current waveform of microgrid
利用矢量拟合法求得电流环加入阻尼控制器后系统聚合阻抗零点见附录A 图A8。可见,加入阻尼控制器后系统聚合阻抗零点全部位于复平面左半平面。时域仿真与矢量拟合法分析表明附加阻尼控制器具有较好的振荡抑制效果。
3 结论
本文通过矢量拟合法对主从控制微电网进行稳定性分析,表明当线路阻抗、本地负荷等参数发生变化时,系统可能出现振荡失稳现象。本文所提算法简便易行且无需获取DER 内部详细参数即可定量分析微电网稳定性,具有较高的工程实用性,更符合工程实际应用场景。
此外,本文提出的基于矢量拟合法分析结果的DER 控制参数优化设计方法、附加阻尼控制器控制方法,能够有效提高微电网的稳定性。
(本刊附录请见网络版,印刷版略)
