“车−站−路−网”系统中时空分布充电电价的优化
2021-12-20张学军韩鹏
张学军,韩鹏
(山西大学电力与建筑学院,山西省 太原市 030013)
0 引言
随着交通电气化的发展,电动汽车(electric vehicle,EV)将替代燃油汽车成为主要的交通工具。大量EV 的充电需求不仅加大了电力网(power network,PN)的运行负担[1],而且因充电而增加的通行需求对交通网(traffic network,TN)的运行也会产生额外影响[2-3]。EV 对PN 和TN 运行状况的影响的程度必将成为城市承载EV能力的主要制约因素。
EV 的大规模使用,不仅对PN 和TN 的运行产生巨大的影响,同时还使原来不甚相关的PN与TN 间产生了复杂的耦合关联,形成了“车−站−路−网”系统。系统中的关联耦合主要表现在:EV 充电增加了PN 的负荷和TN 的交通流量;充电站(charging station,CS)的配置、充电价格、TN 的结构和拥堵程度对EV 的电能消耗、行驶路径选择和CS 的充电负荷产生影响,从而影响充电负荷和交通流量的时空分布;充电负荷和交通流量的分布反过来又影响CS 充电价格的决策。
EV 充电对PN、TN 和CS 的影响与其在空间和时间2 个维度上分布的充电行为有密切关系。目前研究集中于应用充电价格引导EV 有序充电来优化PN 的运行状况方面。文献[4]假设响应分时电价的EV 的比例为常数,应用遗传算法求出了峰谷电价时段;文献[5-6]考虑充电费用、PN的安全性及用户满意度建立了分时充电电价优化模型;文献[7]建立了分时电价制度和电动汽车调度的主从博弈模型以平抑负荷均方差;文献[8-10]在优化模型中分别应用电量电价弹性矩阵、响应度和负荷转移率描述了EV 驾驶员对电价的响应。
PN 和TN 是现代城市基础设施的重要组成部分。如前述,在EV 的应用和发展所形成的“车−站−路−网”系统中,存在着诸多复杂的时空关联耦合关系,仅考虑EV 与PN 的相互影响,采用不考虑空间位置差异的单一分时充电价格,难以有效地提高城市运行质量和承载EV 的能力。本文从系统的角度出发,考虑系统中各类实体间的相互影响建立模型,研究采用时空分布电价(同一时段内不同充电站的充电价格不同)引导EV有序充电,同时优化PN 和TN 运行的有关问题。
1 “车−站−路−网”系统模型
1.1 交通网络
将城市按功能分为居民区(H)、工作区(W)和其他区(O),TN 可用道路为支路,区域和交叉点为节点的网络来描述,即
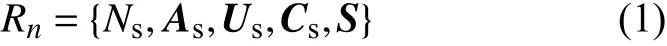
式中:Ns为区域的集合;As为n阶区域邻接矩阵,n为区域数;Us和Cs为与As同阶的矩阵,其元素分别为区域间道路的设计车速(km·h−1)和通行能力(pcu·h−1);S为n维向量,其元素为区域的地理坐标,用来计算区域间有向道路在平面上的角度矩阵和长度矩阵。
As矩阵的元素为
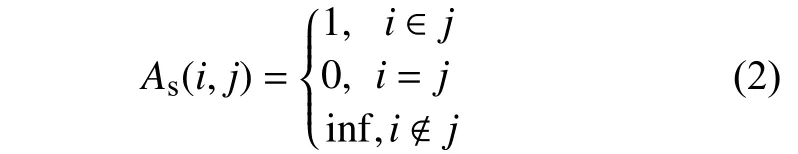
式中:i∈j和i∉j分别表示区域i到区域j有、无邻接道路。
1.2 交通出行
1.2.1 出行空间特征量
出行空间特征量描述了EV 出行目的地的统计特性。本文用图1 所示马尔科夫状态转移图来描述EV 在不同区域间转移的概率分布。图中:H、W、O 分别为前述3 种区域类型;pij(i,j=H,W,O)为EV 从i区转移到j区的概率,且满足式(3)所示关系。
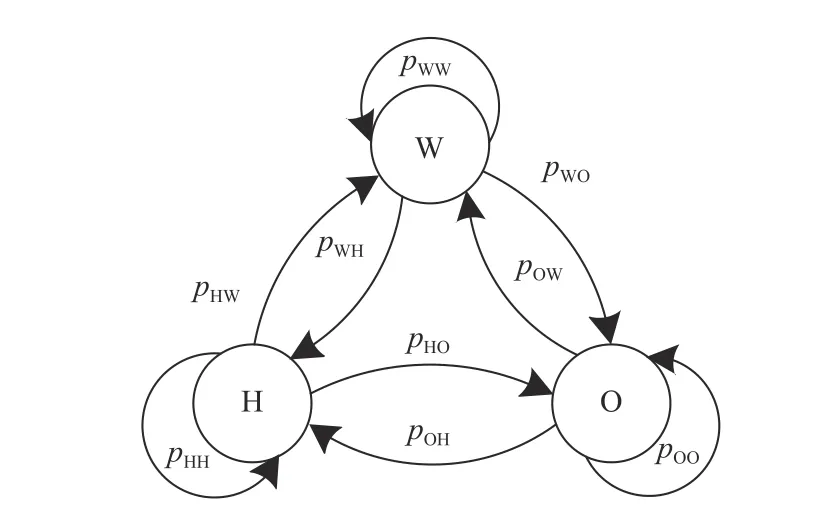
图1 EV 出行状态转移图Fig. 1 EV travel state transition diagram

一种区域类中包含若干区域。为了确定出行的具体目的地,假定区域被选择成为目的地的概率与该区域距当前所处位置的距离成反比,即
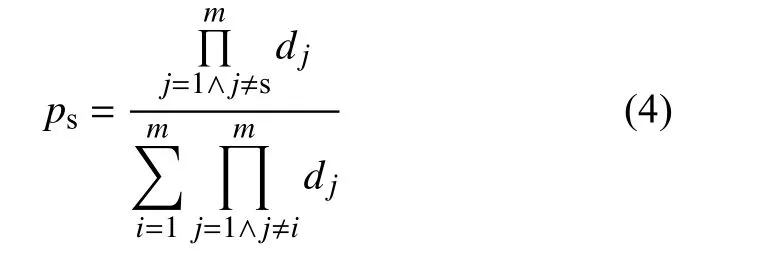
式中:ps为区域s 被选中的概率;m为目的地区域类中的区域总数;dj为第j个目的区域距当前所处区域的距离,km。
1.2.2 出行时间特征量
出行时间特征量描述了车辆首次出行时刻和在不同区域停驻时长的统计规律。不考虑EV 一天的行程中在H 区的停驻,文献[11]的研究表明:车辆首发时刻服从伽马分布,W 区和O 区的停驻时长服从广义极值分布,参数见表1。

表1 出行时间特征量Table 1 Travel time characteristic scale
1.3 电动汽车
1.3.1 通行速度
采用文献[12]交通流量−速度关系模型:

1.3.2 通行速度和荷电状态
文献[13]给出了一种速度−耗电量关系模型,可用来计算耗电功率和荷电状态(state of charge,SOC),即

1.3.3 充电和充电时间
当SOC 不能满足正在进行中的出行、下次出行的需求或SOC 小于0.3 倍额定值时,EV 寻求充电。充电站和路径的选择见第2 节。EV 从接入充电桩开始至充电结束所需时长为
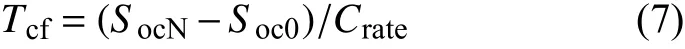
式中:Tcf为充电时长,h;SocN和Soc0分别为额定和当前荷电状态,W·h;Crate为充电功率,W/h。
1.4 充电站和充电负荷
充电站可用先进先出的服务系统来模拟。
充电站的充电负荷可表示为
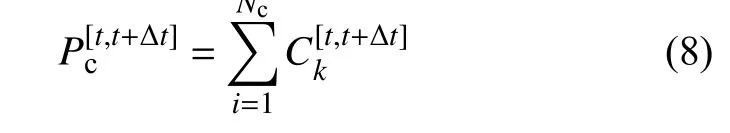
式中:Pc为[t,t+∆t]时段内充电站c 的负荷,kW;Ck为[t,t+∆t]时段内充电站c 的充电桩k的功率,kW;若充电桩k空闲则Ck等于0,否则等于正在充电的EV 的充电功率;Nc为充电站内充电桩的总数; ∆t为仿真步长。
1.5 电节点负荷
假定一个区域由一个PN 节点供电,PN 节点负荷由2 部分组成:

2 驾驶员决策模型
根据人行为的刺激−中间变量−动作模式,可将EV 驾驶员的决策过程分为信息感知、行为决策以及执行修正3 个阶段。
2.1 信息感知
现代信息与通信技术的发展,拓展了EV 驾驶员获得信息的方式和内容。假定EV 驾驶员能实时获得路网结构、充电站位置和道路通行能力等静态信息及SOC、剩余路程、时空分布充电价格、充电站排队长度和交通状况等动态信息。其中交通状况用路段饱和度[12]来表示:

2.2 行为决策
EV 驾驶员基于感知的信息进行通行路径和充电站选择的决策受个体偏好的影响会有较大的差异。偏好具有主观性、抽象性和模糊性等特征,难以用数字确切表达。层次分析法[14](analytic hierarchy process,AHP)用多级标度来量化与决策相关的多因素中两两比较的重要程度,适合于描述不同偏好EV 驾驶员对同一信息的不同响应。
传统的AHP 采用(1—9)标度进行主观评分,难以统一标度标准和保证判断矩阵的一致性。本文采用(0,1,2)三标度法[15]构建间接判断矩阵,给出了EV 驾驶员进行路径和充电站选择决策的AHP 层次结构,如图2 所示。
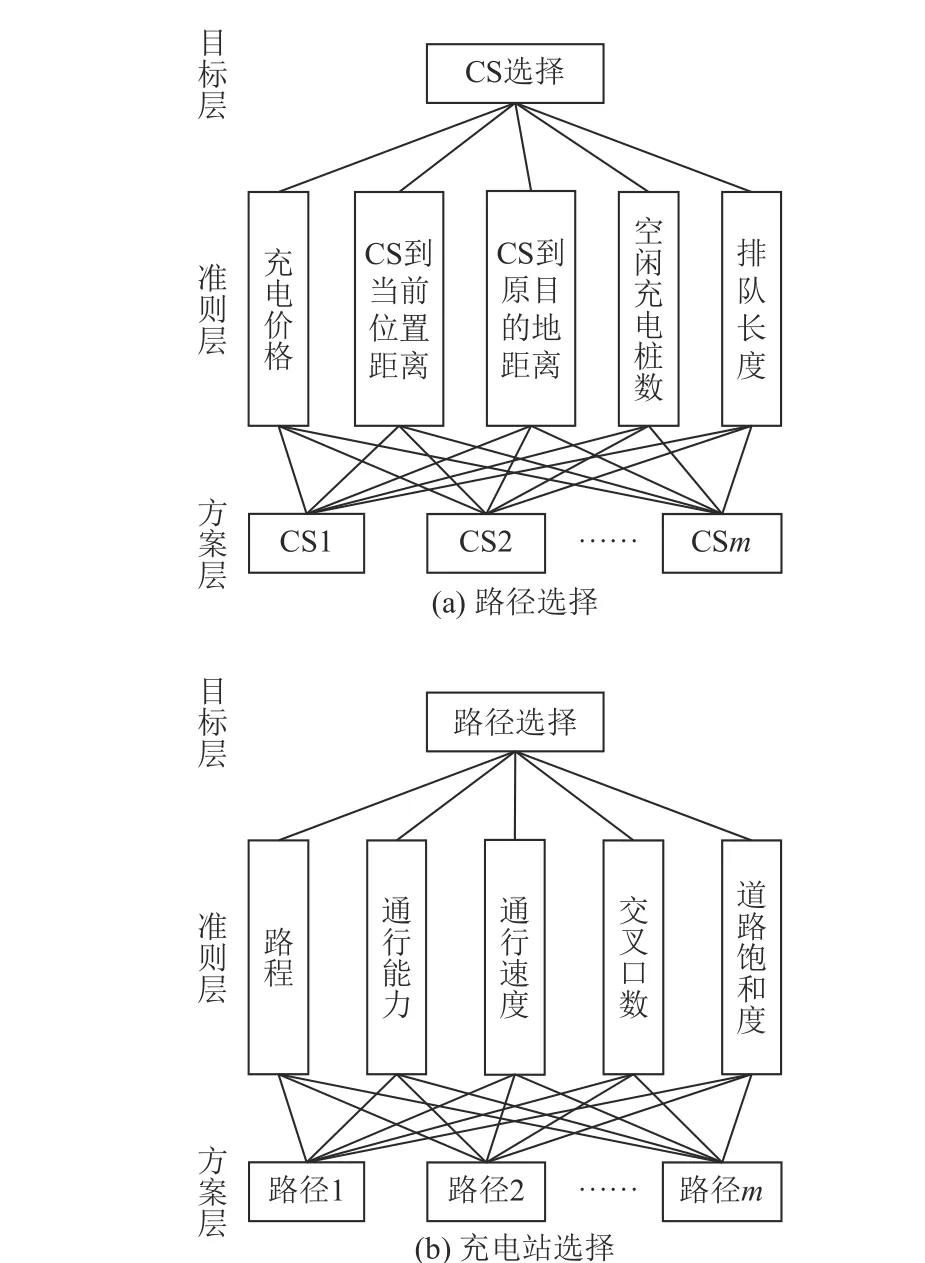
图2 驾驶员决策层次结构图Fig. 2 Driver decision hierarchy chart
在路径选择时,将EV 驾驶员分为:路程优先型、速度优先型和驾驶体验优先型3 种;在充电站选择时,则分为价格优先型、距离优先型和驾驶体验优先型3 种。为每类驾驶员建立不同比较矩阵,就可对驾驶员偏好量化表示。为了进一步细分同种偏好的驾驶员对同一信息响应程度的差异性,在形成判断矩阵时,将准则层、方案层的各比较矩阵最大、最小排序指数之比dm分为5 级:稍微重要、重要、明显重要、强烈重要、极端重要。
EV 驾驶员行为决策的流程如图3 所示。
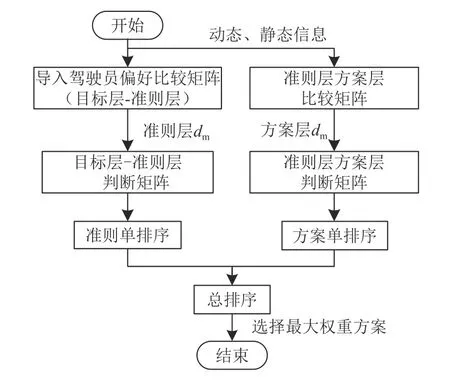
图3 驾驶员行为决策模拟流程Fig. 3 Driver behavior decision simulation process
进行决策模拟时,首先根据不同偏好驾驶员比较矩阵和准则层dm计算目标层−准则层的判断矩阵,并计算权重向量且对n个准则重要程度进行排序。然后对感知的动态、静态信息进行数值比较生成当前环境下的准则层−方案层比较矩阵,根据方案层dm值计算准则层−方案层的判断矩阵,并计算权重向量且对方案重要程度进行排序。最后对两层权重向量进行综合计算,得出对决策目标最高权重的方案。其中,判断矩阵B由式(11)计算,其他部分的计算与传统AHP 一致。
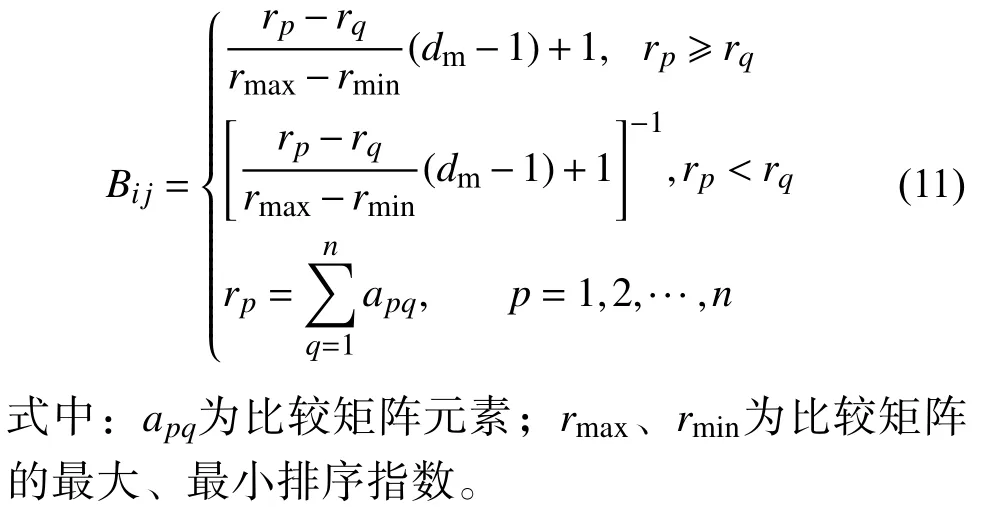
2.3 执行和修正
在决策执行过程中可能感知到信息变化,引发决策修正。但即便是修正了决策,也只能当行驶到TN 节点处才能执行新的决策。因此,将TN 的节点视作有效决策点,驾驶员在其行程中的每个交叉口都会重新感知信息并对决策做必要的修正。
3 时空分布电价优化模型
3.1 优化变量
优化变量为时空分布充电电价。根据消费心理学,价格的变化超过一定的阈值才会引起消费者的有效响应。本文将充电电价分为低、较低、中、较高、高5 个档次,而不是具体的数值。这样,一方面可避免优化结果中出现区分度不高的价格,另一方面便于管理部门结合当地的经济水平制定能充分调动EV 用户响应电价的积极性的分档电价。
3.2 优化模型
1)目标函数。
①PN 有功网损最小:

②TN 拥堵程度最小。
用交通指数(traffic performance index,TPI)[16]描述路网整体的拥堵状况,路网拥堵程度最小的目标表示为

3.3 模型求解
本文优化模型采用带精英策略的非支配排序遗传算法(non-dominated sorting genetic algorithm-II,NSGA-II)求解。为了得到Pareto 解集后从中选出最优折衷解,应用模糊隶属度函数评价解集中对应的各个目标函数满意度。满意度函数如式(15)所示:

优化模型求解流程如图4 所示。
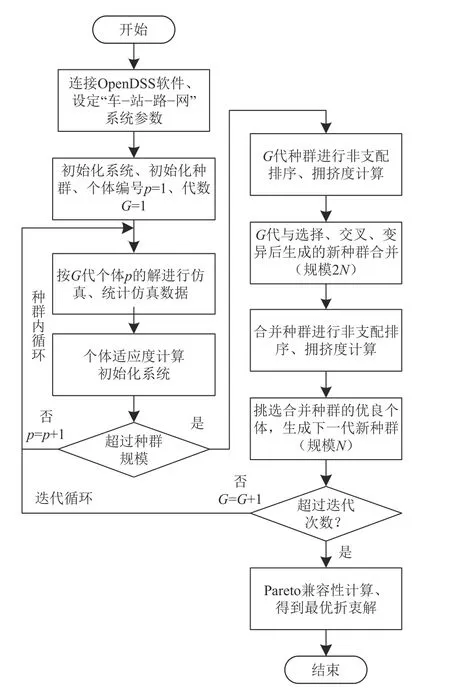
图4 最优充电电价求解流程Fig. 4 Solve loop of optimal charging price
4 算例分析
4.1 基础数据
“车−站−路−网”系统算例如图5 所示。
其中EV 数量为12000 辆,驾驶员路径选择的3 类偏好占比为50%、30%、20%;充电站选择偏好3 类占比为45%、45%、10%;dm的5 级比例为10%、15%、20%、25%、30%;车辆第3次转移目的地为始发区;区域分类和流量−速度关系模型参数如表2、表3 所示;出行空间特征量的相关参数如表4 所示。

表2 区域分类及充电站配置Table 2 Regional classification and charging station configuration

表3 流量−速度关系模型回归参数Table 3 Regression parameters of flow vs. velocity relationship model

表4 出行空间特征量Table 4 Travel spatial characteristic scale
PN 采用IEEE 37 节点配电网模型,各CS 容量统一,CS 与PN 节点的关联如图5 所示,各类区域基础负荷乘数因子曲线如图6 所示。
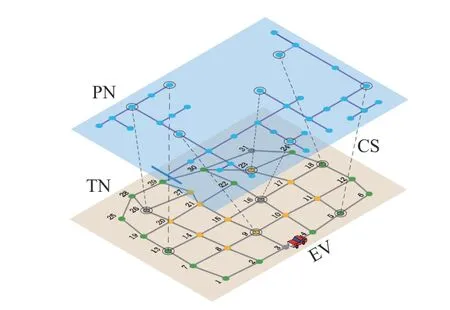
图5 算例系统结构Fig. 5 Structure of the example system
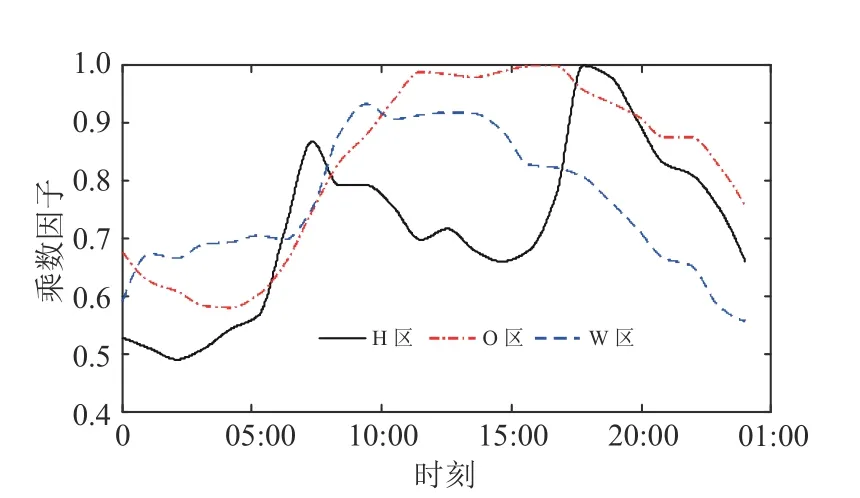
图6 基础负荷乘数因子曲线Fig. 6 Regional base load multiplier factor curve
4.2 电价优化结果
时空分布电价优化结果如图7 所示,由图7可知同一时间不同充电站的充电电价有较大的差异,正是这样的不同强化了电价引导有序充电的作用。
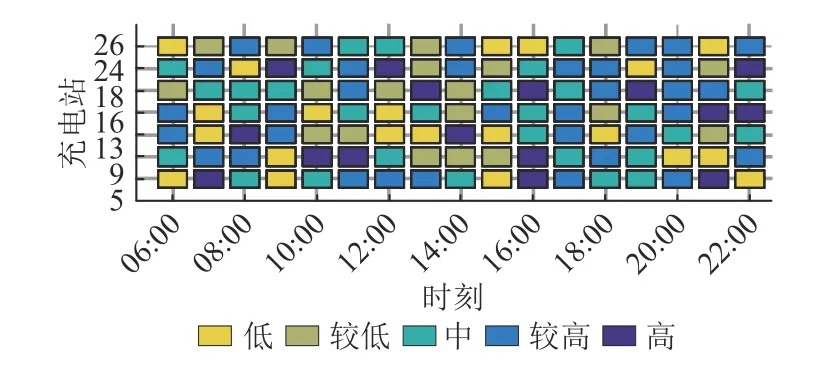
图7 时空分布充电电价优化结果Fig. 7 Optimization results of spatial-temporal distributed charging price
4.3 优化结果分析
以下通过与无序充电方式下PN 和TN 运行状况的比较说明时空分布电价优化模型的有效性。
4.3.1 电网运行状况分析
2 种方式下各CS 充电负荷曲线如图8 所示。
由图8(a)可知:空间分布的不同导致无序情境下出现CS9 的和CS26 充电车辆分配极度不均匀的现象。在时空分布优化方式下,优化模型协调CS 在空间上对EV 负荷的自然吸引力与电价对EV 驾驶员的吸引力,使图7 中CS9 和CS26的电价水平与其余CS 的电价水平在时间与空间上相互配合,而非由于EV 负荷稀少或集中使电价一直维持在低档次或高档次。
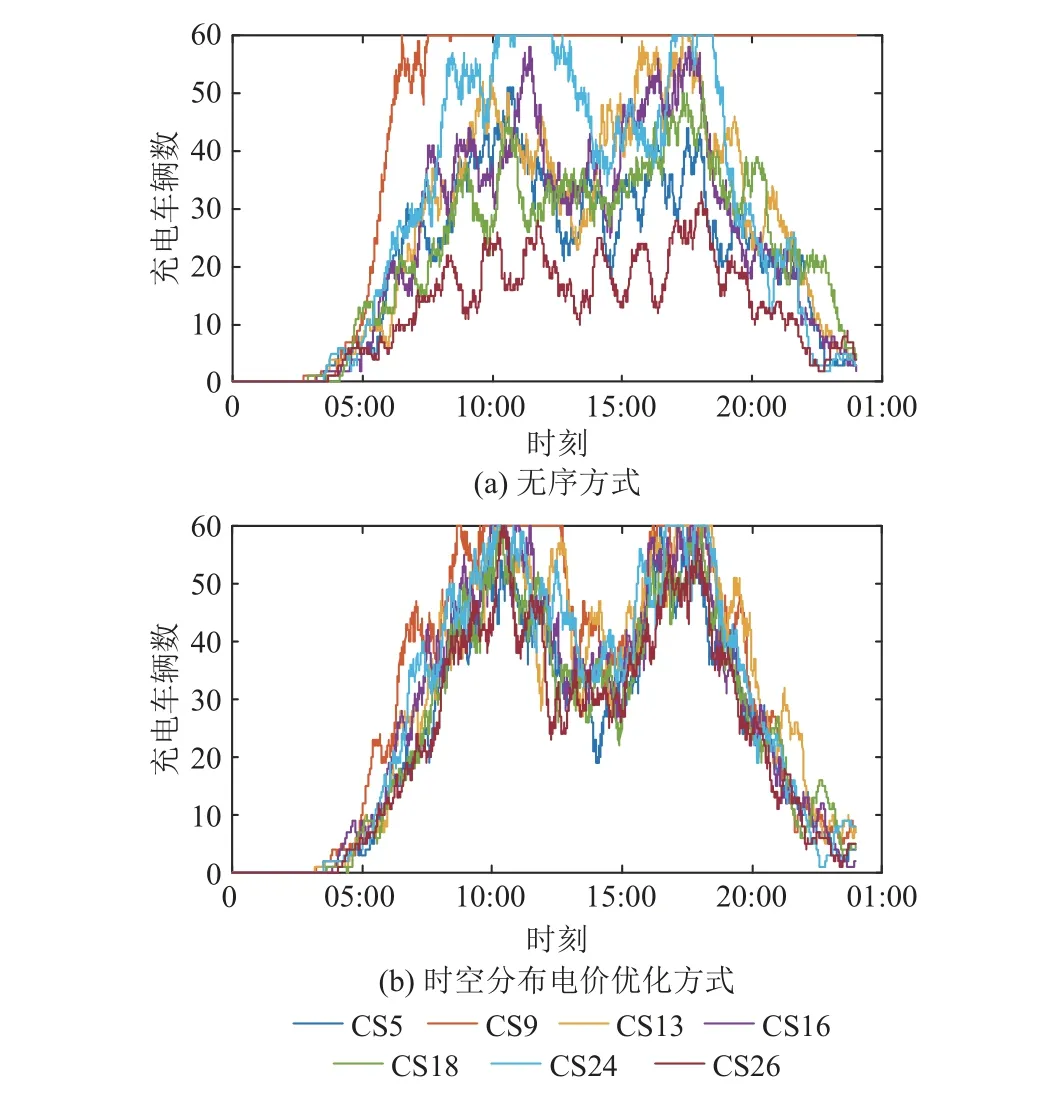
图8 充电车辆数变化Fig. 8 Change in the number of charged vehicles
这样,充电电价与充电负荷在时间和空间2个维度上的配合使各CS 充电车辆总数的标准偏差由图8(a)的155.7701 降至图8(b)的104.2283,缓解了高充电负荷对电网安全的冲击,配电网中负荷的时空分布更为合理,提高配电网整体运行质量。同时,也提高了CS 设备的使用率。
无序方式和时空分布电价优化方式下PN 有功网损和最大电压偏差分别如图9、图10 所示。可见,通过电价引导有效降低高峰期电网的损耗和电压偏差。
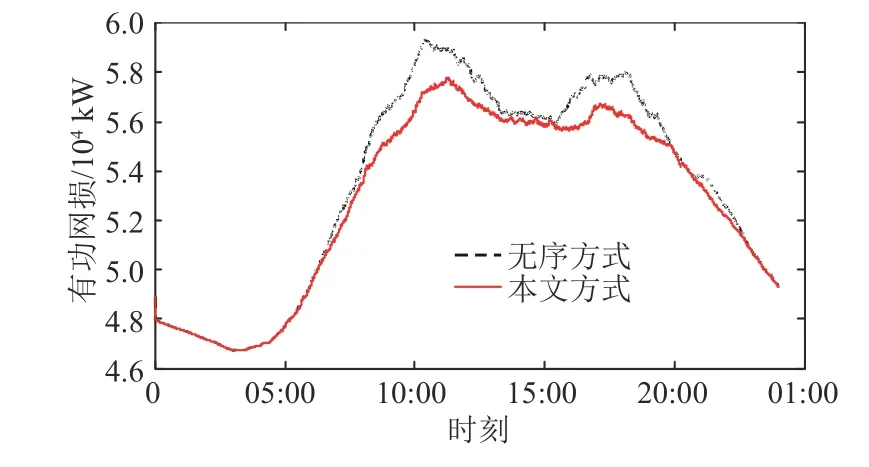
图9 电网有功网损变化Fig. 9 Variation of active power loss in power grid
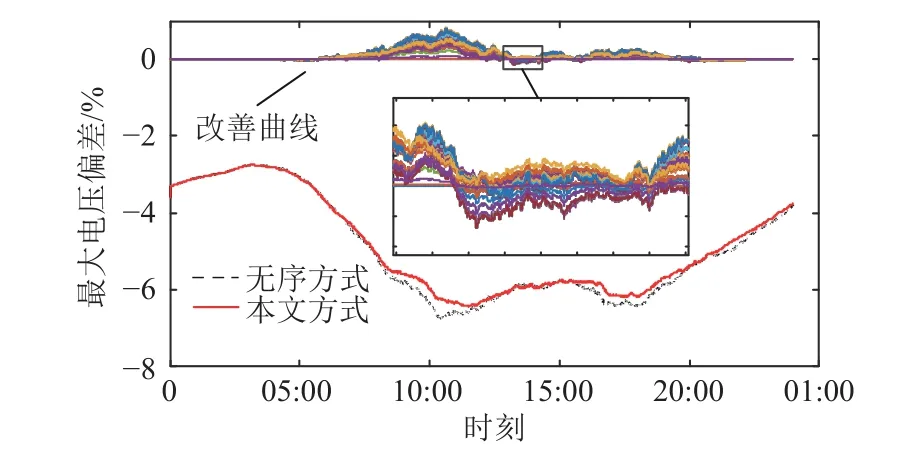
图10 最大电压偏差曲线和电压偏差改善曲线Fig. 10 Maximum voltage deviation curve and voltage deviation improvement curve
在图10 中观察到部分时段2 条曲线有轻微交叉,说明时空分布电价将高负荷充电站流量被吸引至其他电价较低的充电站,使部分低价CS 负荷增加。用无序方式下PN 所有节点的电压偏差值减去时空分布电价优化方式下PN 所有节点的电压偏差值得到的图10 上部所示的电压偏差改善曲线。可知EV 负荷的时空挪移对部分PN 节点的电压有轻微的不利影响,但PN 电压仍运行在允许范围内。
4.3.2 交通网运行状况分析
图11 表示了2 种方式下道路全天总流量。可见,采用时空分布电价优化后车流在空间上的分布由极端变为均衡,各道路车流量总标准偏差由360.1367 降为235.9438,交通流量在空间分布上的离散程度明显减小。
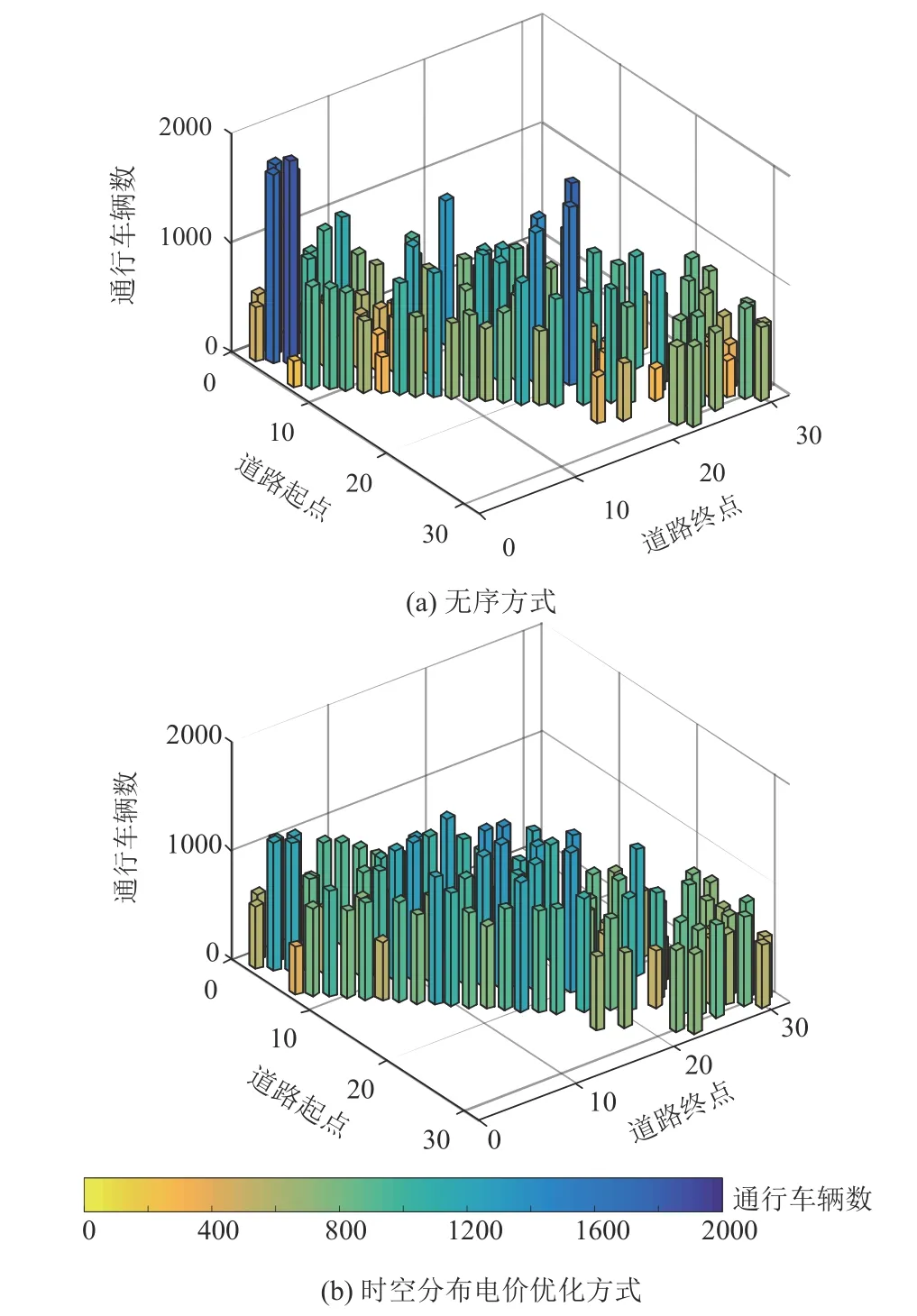
图11 道路通行流量Fig. 11 Statistics of road traffic flow
TPI 是评价TN 拥堵程度的指标,分为5 级,级差为2,TPI 等级由低到高分别对应路网拥堵情况中的非常畅通、畅通、轻度拥堵、中度拥堵、严重拥堵。图12 为无序方式、时空分布电价优化方式TPI 的变化曲线。
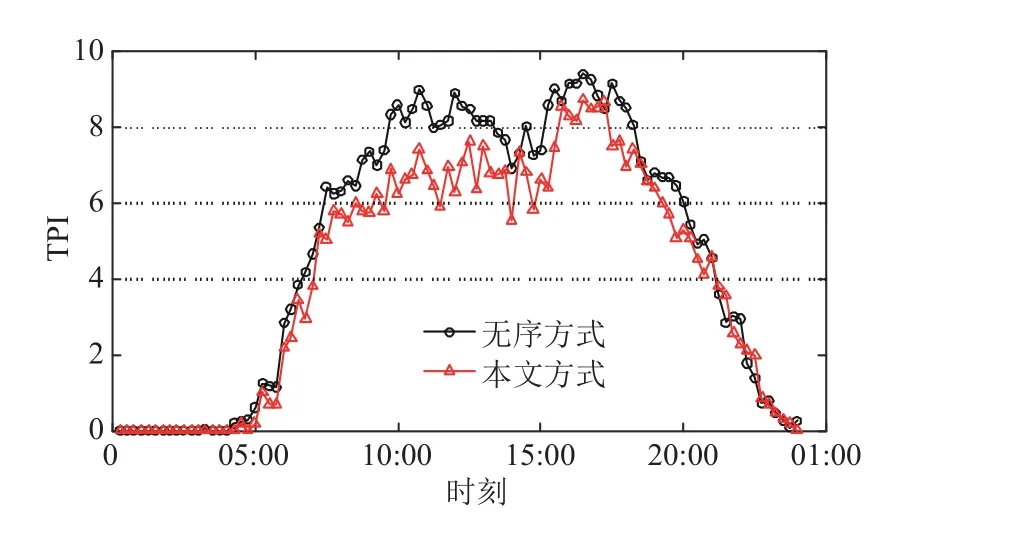
图12 交通网拥堵程度变化Fig. 12 The change of traffic performance index in transportation network
可知:在采用时空分布优化电价后,各统计点处CS 电价分布的空间差异影响寻求充电的EV 驾驶员决策,使TN 发生严重拥堵的统计点数由29 降低至7,中度拥堵点数由22 升至31,轻度拥堵点数由7 升至18。不仅减少了TN 发生恶劣拥堵的情况,且各等级内的拥堵程度也有改善。
5 结论
1)从“车–站–路–网”系统的角度出发,同时考虑EV 对PN 和TN 的影响,能较全面地研究交通电气化情景下PN 和TN 的协同规划和运行控制等有关的问题。
2)采用时空分布充电电价来引导EV 的出行和充电,能从时间和空间2 个维度上优化PN 的充电负荷分布和TN 的交通流量分布,对提高PN 和TN 的运行质量和城市承载EV 的能力有积极意义。
3)驾驶员是EV 出行和充电的实际控制者,在相关研究中应考虑驾驶员行为决策的个体差异性。采用AHP 量化模拟驾驶员的决策过程,能比较精细地刻画影响不同类型驾驶员决策的因素,有助于得到更符合实际的结果。
