考虑场景聚类的配电网−天然气联合系统双层随机运行优化

唐海国，张志丹，康童，张帝，张聪，罗波

（1. 国网湖南省电力公司电力科学研究院，湖南省 长沙市 410007；2.湖南大学电气与信息工程学院，湖南省 长沙市 410082；3.国网湖南省电力有限公司检修公司，湖南省 长沙市 410007）

0 引言

为应对化石能源对全球气候变化带来的挑战，我国大力推动间歇性新能源的发展[1]。然而，由于间歇性新能源发电具有强随机性和不确定性的特征，给电网安全运行带来了极大的挑战，进而我国弃风弃光等问题日益严重[2]。配电网与天然气网相互耦合、相互联合系统可以达到提高能源效率的目的[3-4]。因此，研究考虑风电接入的配电网−天然气网联合系统运行优化方法具有重要意义。

目前，针对配电网−天然气网联合系统运行优化的研究主要关注环境友好性和效益性。文献[5]提出可以通过电转气机组的电转气（power to gas，P2G）功能将电能转为天然气，并通过燃气机组将天然气转为电能，建立了基于稳态流的电气耦合系统环保运行优化模型。文献[6]针对天然气调压站及其液化全过程，提出了考虑天然气压力能的配电网−天然气网耦合系统调度优化模型。文献[7]针对天然气系统中气量供应不足以及天然气网络传输容量有限的情况，构建了多源配电网与天然气网协同运行优化模型，并通过粒子群算法求解所提非线性规划模型。文献[8]考虑系统发电的能源成本和碳交易成本，建立了电气互联综合能源系统和单纯火电机组电力系统的低碳经济模型。但现有文献大多假设综合能源系统内的间歇性发电机组出力为固定值，因而运行优化策略难以有效应对间歇性发电机组的波动性。

现有针对含风电综合能源网运行优化的报道大多采用随机规划的数学方法，通过海量功率来刻画间歇性能源的不确定性。文献[9]采用Monte Carlo 模拟方法生成表示风电和负荷不确定参数的场景，并构建了一种基于场景间距离的场景约简算法以在一定程度上削减场景，从而建立基于场景削减的天然气和电网运行的两阶段随机运行优化模型。文献[10]基于间歇性电源的概率密度分布，通过改良版的多线性Monte Carlo 抽样方法抽取间歇性电源出力场景，建立了考虑间歇性电源多随机场景的配电网−天然气网系统概率潮流模型。文献[11]通过预留系统备用的方式，建立了考虑风电备用优化的多区域配电网−天然气网系统日前调度模型，并提出了参数自适应的交替方向乘子法（alternating direction method of multipliers，ADMM）算法以有效求解模型。文献[12]以机会约束的形式考虑风电随机波动场景，并通过Bernstein 近似理论将其转化为确定性运行优化问题。然而，由于Bernstein 近似理论只能针对某些特定的机会约束形式，需进一步探索其普适化转化方法。文献[13]提出可以通过引入天然气定价的调整机制来提高网络接入间歇性电源的能力。文献[14]提出温控负荷调节的方法来降低综合能源系统的运行成本，同时有利于消纳间歇性能源。文献[10-14]基于随机规划数学模型具有应对间歇性能源随机性的能力，但随机抽样所考虑的无数随机场景大大增加了求解综合能源系统运行优化模型的难度。文献[15]提出了核密度聚类算法将海量风电场景聚类为少数风电场景以表征风电不确定性，降低了配电网−天然气系统模型求解规模和难度。然而，该方法需主观事先假设风电聚类场景数目，而聚类场景数目会极大地影响聚类效果和运行优化方案。

为了表征风电出力随机性并合理权衡聚类场景数目对系统运行优化模型求解的影响，本文在降维数据的基础上构建了基于分层聚类算法的风电随机场景选取方法，并提出最优聚类类数的确定标准以有效划分风电场景类数。此外，本文提出了基于分层场景聚类法的配电网−天然气网耦合系统双层随机运行优化方法，从中长期和短期（包括日前和日内实时两个阶段）应对风电不确定性。

1 整体框架

间歇性电源机组出力易受多种环境因素的影响，其发电功率表现为较强的随机性和波动性。以我国某间歇性电源机组运行功率为例(见图1)，其出力在一年内呈现极强的波动和不确定。

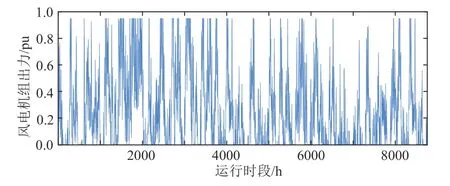
图1 间歇性电源机组出力Fig. 1 Output of an intermittent power generating unit

系统决策者在制定运行优化策略时，若仅考虑风电预测场景而不考虑风电波动，得到的运行策略极可能因为风电波动而无法在实际中应用。然而，若将所有的风电场景带入运行优化模型，则模型会因为海量的风电场景而不可行。

针对以上问题，本文所提方法包括2 个方面。1）在典型风电场景选取方面：基于分层聚类法，将海量的风电场景聚类为若干有代表性的典型场景，以科学合理权衡聚类场景的数量与聚类效果，主要包括3 个部分，基于主成分分析法的数据降维、对风电场景聚类分析、最优聚类类数的确定。2）在运行优化方面：在风电聚类场景的基础上，从中长期、日前和实时3 个时间尺度，构建了基于场景聚类的配电网和天然气网多时间尺度双层随机运行优化模型。

需要指出的是，风电场景的聚类与配电网−天然气耦合系统运行优化这两部分具有密切联系，风电场景聚类的优劣将极大地影响耦合系统运行优化阶段的策略。若风电场景的聚类类别数过少，则聚类后的风电场景往往不具典型性，因而基于聚类场景所得到的运行优化策略极可能不可行。相反地，若风电场景的聚类类别数过多，将给耦合系统运行优化带来计算困难，难以满足实际工程的计算时间要求。本文所提的配电网−天然气联合系统双层随机运行优化整体框架可参考图2。

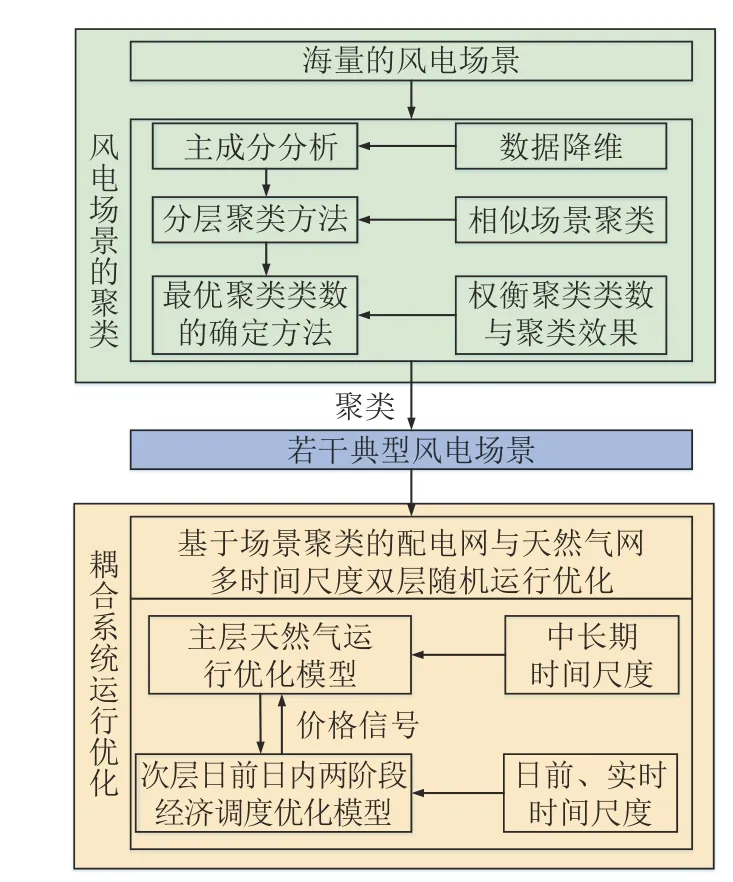
图2 整体框架示意图Fig. 2 Schematic diagram of overall framework

2 基于分层聚类的风电场景生成

2.1 基于主成分分析法的数据降维

当风电场景数较多时，难以直接对风电原始数据进行聚类，因此本文首先基于主成分分析法对海量的风电场景进行数据降维，提取重要的特征数据，以提高聚类效率。

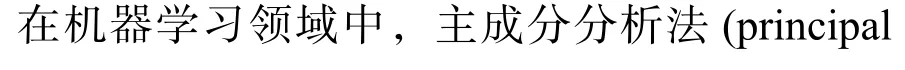
单个特征保留程度指标数值 ϖt越大，则说明其对应的主成分分量zt包含越多的风电出力数据内部信息。相似地，特征保留程度指标数值ϖˆt越大，则说明前t个主成分分量z1,z2,···,zT1包含的风电出力数据内部信息越充足。因此，可以通过特征保留程度指标 ϖˆt选取合适的降维维度以权衡计算复杂度和原始数据信息保留程度的矛盾。

2.2 基于分层聚类的风电场景聚类分析

式中：na和nb分别为场景类Ga与场景类Gb的场景数量。

基于以上定义，本文给出分层聚类的具体流程如下文所述。

1）将每个风电场景分为一类，则得到N类风电场景，每类风电场景可表示为

6）场景类数量减少1，即N−1。

以上为一次完整的聚类流程，每次迭代总场景数量均减少1，不断重复上述聚类，直至所有的风电场景合为一类，其分层聚类直观示意如图3 所示。

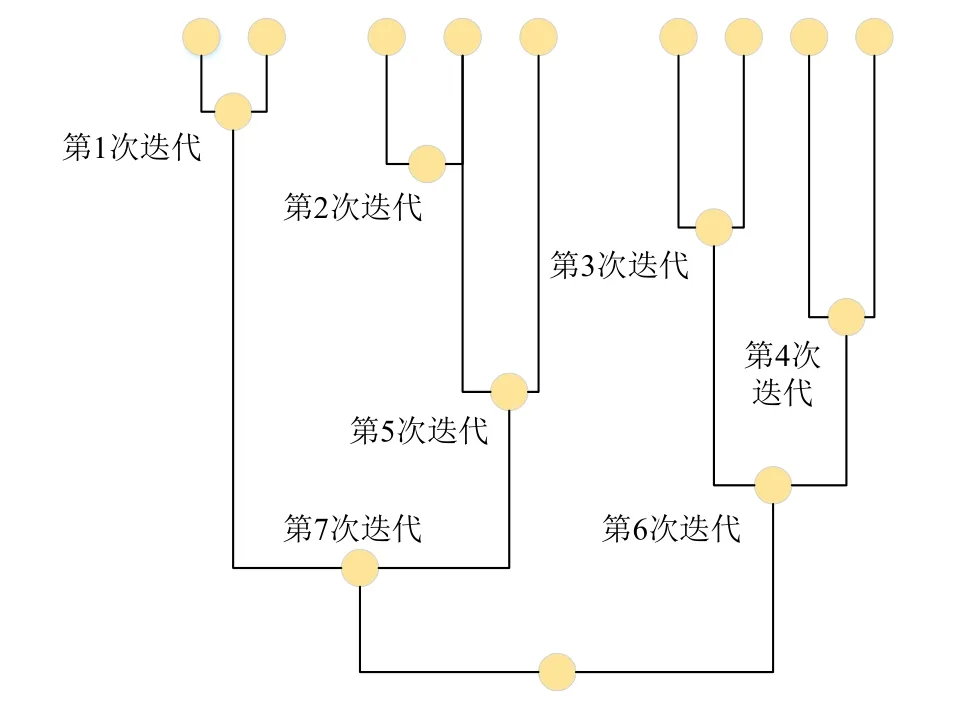
图3 分层聚类直观图Fig. 3 Pictorial diagram of hierarchical clustering

2.3 最优聚类类数的确定

由于聚类类数会对聚类质量和运行优化效率有较大影响，若聚类类数较少，则聚类后的场景可能难以充分代表所有场景；若聚类类数较多，则由于场景间特征不明显而不具代表性，同时也给后续系统运行优化模型带来求解困难。因此有必要合理选取最优聚类类数以合理权衡聚类场景的数量与聚类效果。首先，为了定量评估聚类后每一类风电场景内部的紧凑程度，本文定义类内的集中度Br为该类中所有风电场景与该类中心场景Zr的欧几里得距离：

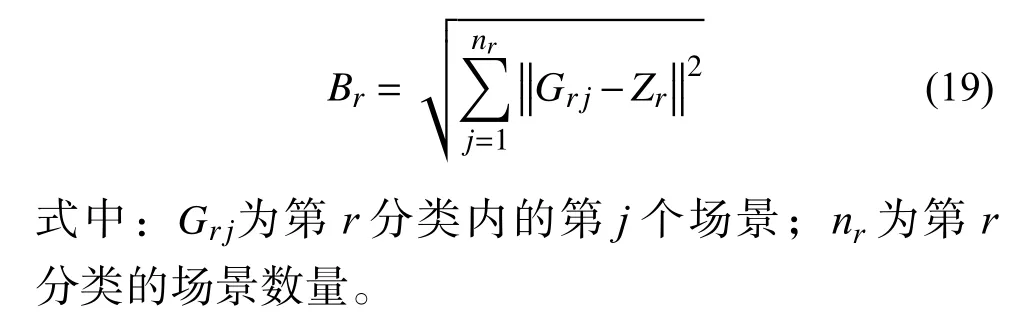
此外，为了定量评估聚类后类与类场景之间的分散程度，本文定义类间的分散度B为每类中心点与所有场景中心点Z的欧几里得距离：

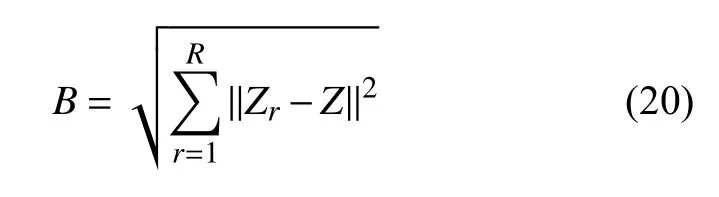
式中R为分类的总数量。

为了综合考虑类内集中度指标Br与类间分散度指标B，本文进一步提出了综合聚类指标O(R)：

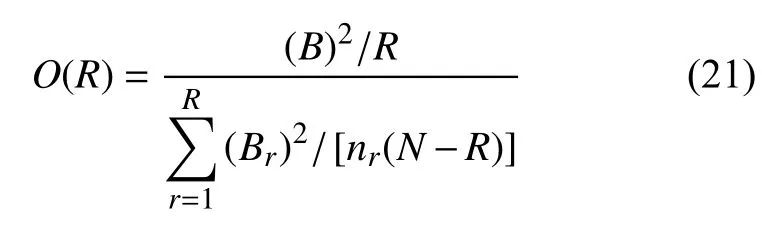
因此，综合聚类指标O(R)表征为类间分散度指标B与类内集中度指标Br的比值。若综合聚类指标O(R)越大，则意味着各类内部场景越紧凑，类与类之间的区别界限越明确，因此代表着聚类的效果越佳。反之，则意味着各类内部场景越分散，类与类之间的区别界限越模糊，聚类的效果越差。因此，通过比较不同聚类数情况下的综合聚类指标O(R)，可以有效地选取最优聚类类数R，避免人为主观选取R所带来的盲目性。

3 考虑场景聚类的配电网和天然气网多时间尺度随机运行优化模型

为了使本文模型更具普遍性，本文以典型配电网−天然气网联合系统(如图4 所示)为例建模，该联合系统主要包括配电网系统、天然气网系统以及衔接两系统的燃气发电机，配电网包含火电机组、风电场以及配电网内的电力负荷，而天然气网包含天然气生产机组和天然气负荷。在未来高比例风电并网下，配电网与天然气网的联合协同运行，可提高网络应对风电出力不确定性的能力，进而促进风电的消纳。

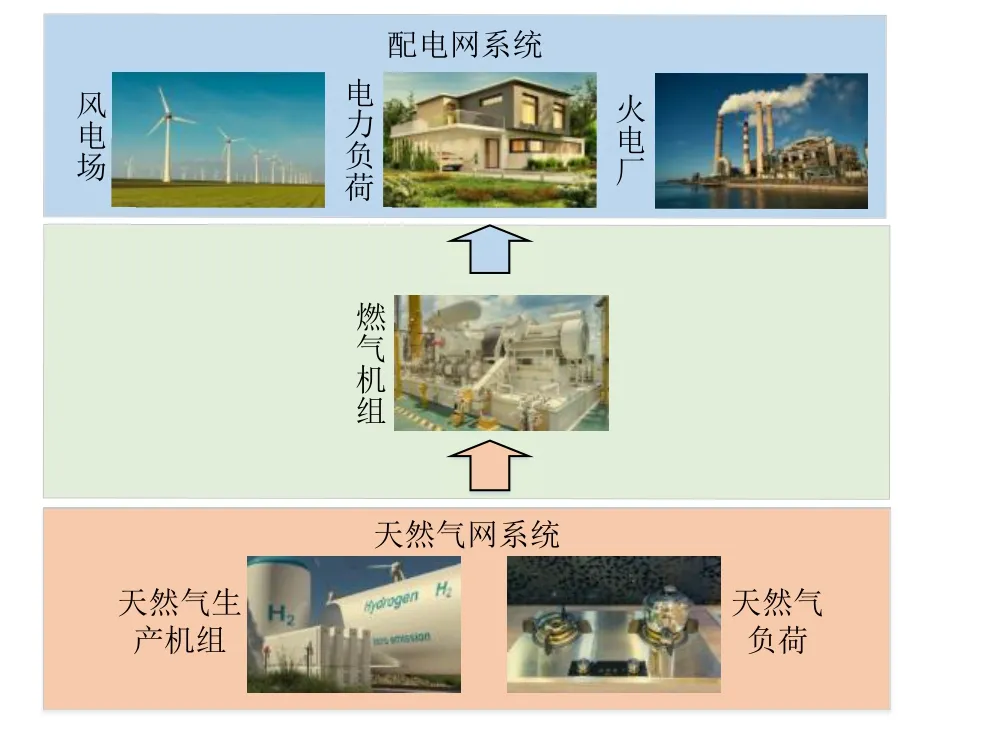
图4 配电网−天然气网Fig. 4 Integrated distribution network with natural gas network

当前研究表明，随着时间尺度从中长期到短期的缩短，风电预测误差逐步减小。因此，本文建立了基于场景聚类的配电网和天然气网联合系统双层随机运行优化模型以充分消纳风电，其中，主层优化模型为中长期运行优化时间尺度，主要调整中长期的天然气价格以使得综合能源网络总运行成本最优，而次层优化模型则为日前和日内实时两阶段经济调度优化，优化目标包括配电网火电机组的发电成本、天然气网产气成本，以及日内实时阶段的运行成本，其结构模式如图5 所示。

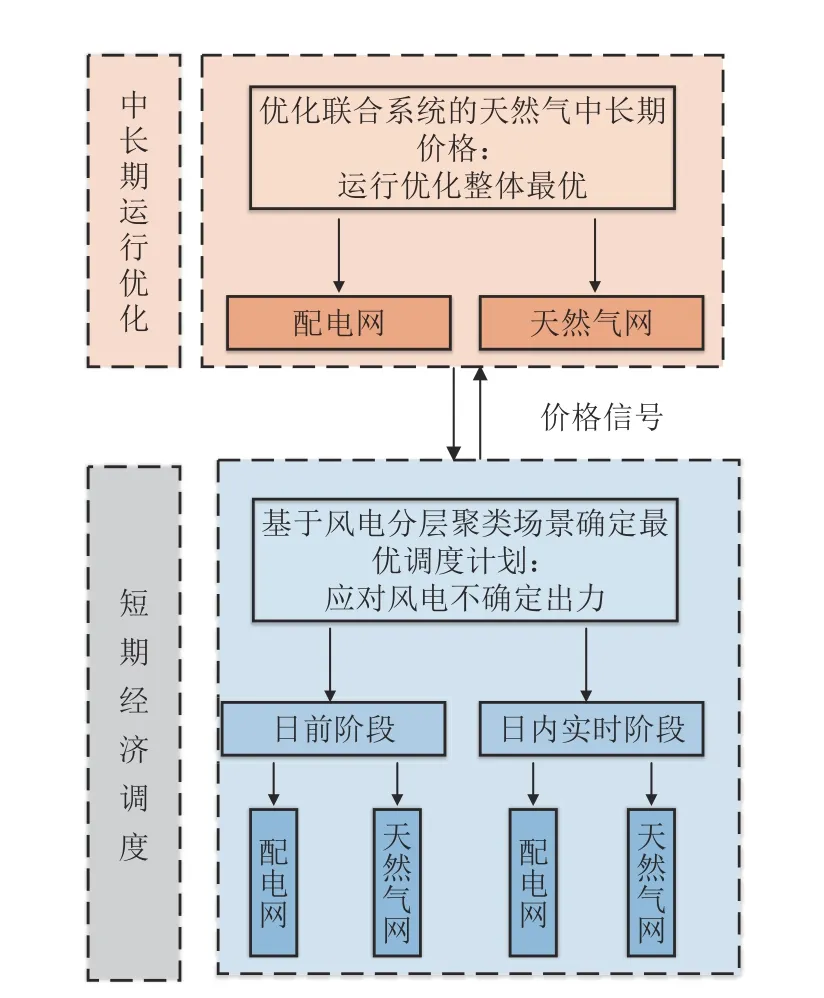
图5 双层运行优化模型Fig. 5 Optimization model of bi-level operation

3.1 主层天然气价格运行优化模型

3.2 次层日前−日内两阶段经济调度模型

以应对日内实时风电不确定性，同时使得联合系统实时再调度成本最小，包括配电网中的火电机组发电功率调整成本、燃气机组发电功率调整成本、切负荷成本、弃风成本以及天然气网中的天然气生产机组发电功率调整成本和切气负荷成本。因此，次层模型的目标函数可表示为

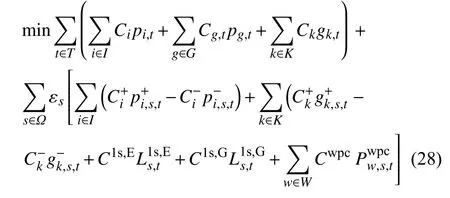
为了便于表示，本文将火电机组I和燃气机组G统称为可调度电力机组U，用集合可表示为U=I∪G。

联合系统日前−日内两阶段经济调度模型的约束包含日前发电调度约束和实时发电调度约束，其中，联合系统日前发电调度模型需满足的约束如下文所述。

1）可调度电力机组的出力约束：

联合系统实时发电调度模型需满足的约束如下文所述。

8）可调度机组的功率调节范围约束：

4 双层调度模型求解

区别于传统单层运行优化问题，本文所建模型是一个带有平衡约束的数学优化问题(mathematical optimization with equilibrium constraints，MOEC)，在数学本质上为斯塔科尔伯格博弈优化问题[17]，在求解算法上为NP-hard 问题，求解难度较高，难以通过传统单层数学优化算法求解。

为了有效求解所建模型，本文通过引入拉格朗日因子，并利用KKT 条件将下层的线性运行优化问题以KKT 约束形式表征，进而将与上层优化模型合并，从而将双层优化模型合并转化为单层优化问题。

为了便于理解和推导，本文将所提的斯塔科尔伯格博弈模型可分为主层模型和次层模型，其一般形式可表征如下：

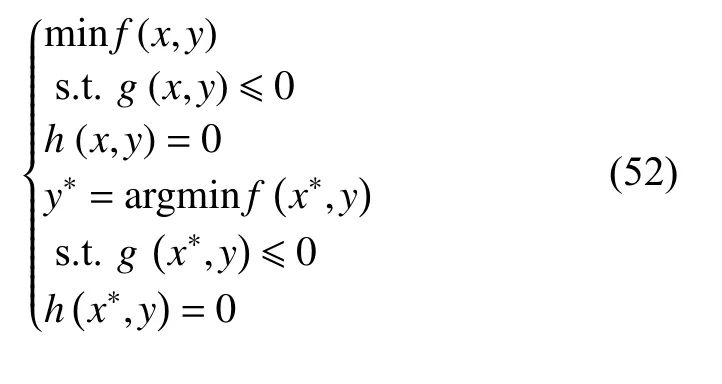
式中：x、y分别对应于主层和次层优化模型的决策变量；f(·)对应于主层优化目标；g(·)、h(·)分别对应于主层优化的不等式约束和等式约束；f(·)对应于次层优化目标；g(·)、h(·)对应于次层优化的不等式约束和等式约束。

因此，在斯塔科尔伯格博弈双层优化模型中，主层模型为同时融合主层模型与次层模型全部变量的决策优化，而次层则为在主层决策变量给定下的运行优化，2 层之间相互制约、相互依赖。对此，本文用 γ、 α分别表示斯塔科尔伯格博弈双层优化模型(式(52))的次层优化模型不等式约束和等式约束的对偶变量。

根据KKT 最优性条件，次层模型的最优解等价于以下方程解：

因此，通过引入朗格朗日因子和利用KKT条件，可将本文所提斯塔科尔伯格博弈优化模型转为单层数学规划问题，进而可调用目前高性能的数学优化求解器求解。

5 算例分析

为了验证所提基于场景聚类的配电网−天然气网随机运行优化模型的有效性，本文在修正的IEEE 14 节点配电网[18]和天然气网耦合系统基础上编程仿真。该耦合系统包含3 台火电机组，2台燃气机组，2 台天然气生产机组和1 个风电厂，耦合系统机组具体参数见表1 和表2。

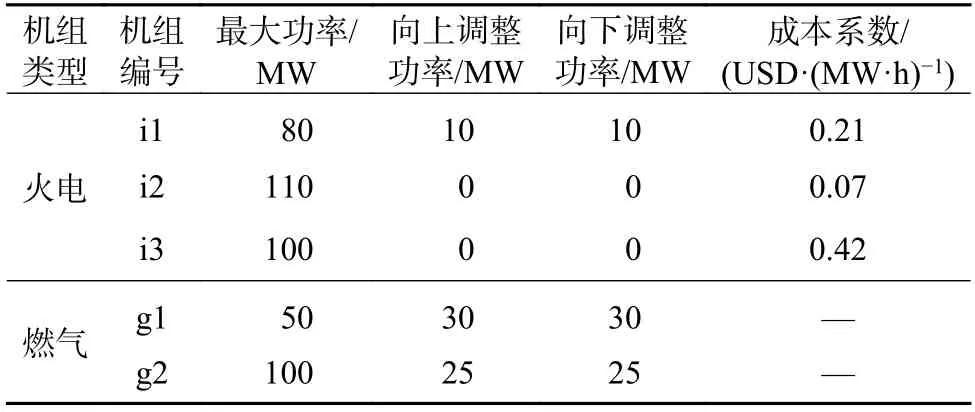
表1 配电网机组参数Table 1 Parameters of generating sets in distribution network

表2 天然气机组参数Table 2 Parameters of generating sets in natural gas network

配电网系统中风电机组典型日的预测出力曲线、电负荷曲线以及天然气网系统的气负荷曲线如图6 所示，其中基准电负荷值为500 MW，基准气负荷值为100 km3/h，基准风电出力值为300 MW。

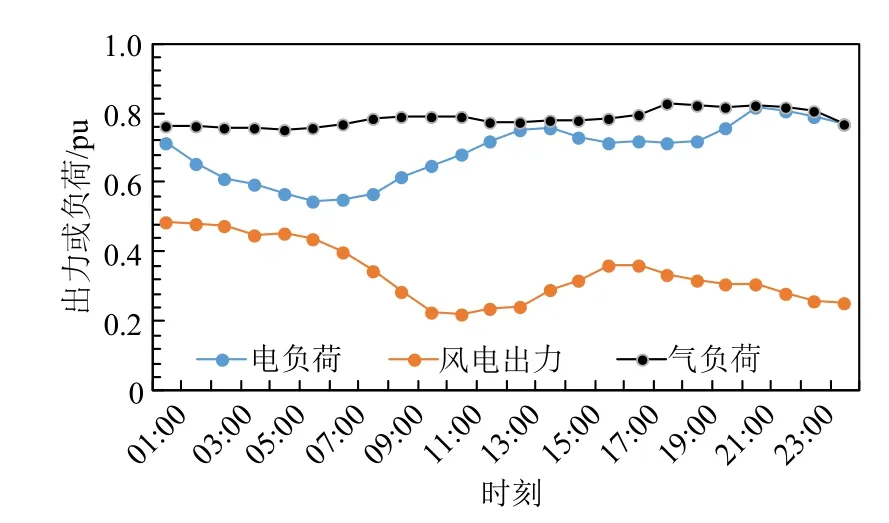
图6 电负荷，气负荷和风电预测出力的标幺值曲线Fig. 6 Per unit value curves of electrical load, gas load and predicted output of wind power

为了更真实客观地表征风电的实际出力，本文取西北电网某实际风电场历史出力进行分析。根据风电出力历史数据可知，由于风电机组出力受环境因素影响较大，具有较强不确定性和随机性，风电的实际出力将在其典型日出力附近随机波动，如图7 所示。

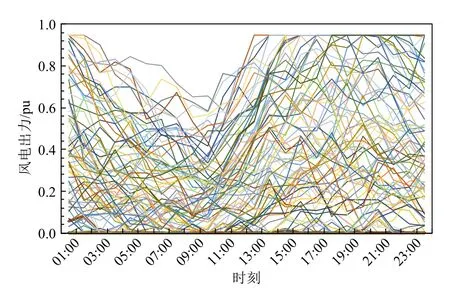
图7 风电随机出力场景Fig. 7 Wind power random output scenarios

为了验证所提分层聚类算法的有效性，本文在Jupyter Notebook 环境下编写PCAM 数据降维算法、聚类算法及相应评估程序，并在GAMS 运筹优化软件中编写随机运行优化程序，通过调用Cplex 商业数学求解器求解KKT 转化后的模型，其中算法的相对求解精度设置为10−5。计算机软件环境为Windows 10，内存RAM 为16 GB，处理器CPU 为Intel(R) Core ™ i7，主频为3.20 GHz。

5.1 场景生成分析

由于风电场景数过多，直接进行聚类将带来维数灾难问题。因此本文先对风电场365 天每天24 h 维度的历史数据进行降维处理，提取数据的关键特征，特征保留程度与保留特征维数的关系如图8 所示。

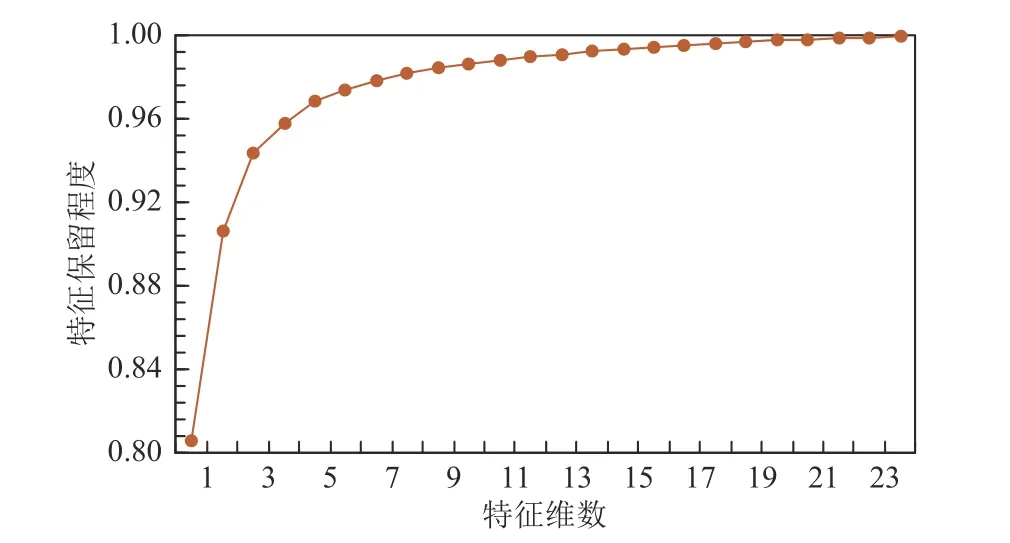
图8 特征保留程度与保留特征维数的关系Fig. 8 Relationship between the feature preserving degree and the dimensions of preserved features

从图8 可看出，随着特征维数的增多，特征保留程度数值越大，降维后的数据包含越多原始数据特征和信息。当特征维数取为24 h，由于降维后的风电出力数据与原始风电出力数据维度相同，此时特征保留程度为100%，然而此时数据维数和计算复杂度也最高。可以观察到，当保留特征维数取为3 维时，可以有效保留95%的数据信息，再往后增幅并不明显，因此本文保留3 维特征维数以合理权衡计算复杂度和数据信息保留精度。

为了验证所提分层聚类算法的聚类效果，本文将其与目前先进的密度聚类算法[15]进行对比，并通过综合聚类指标O(R)评估其优越性，如图9所示。

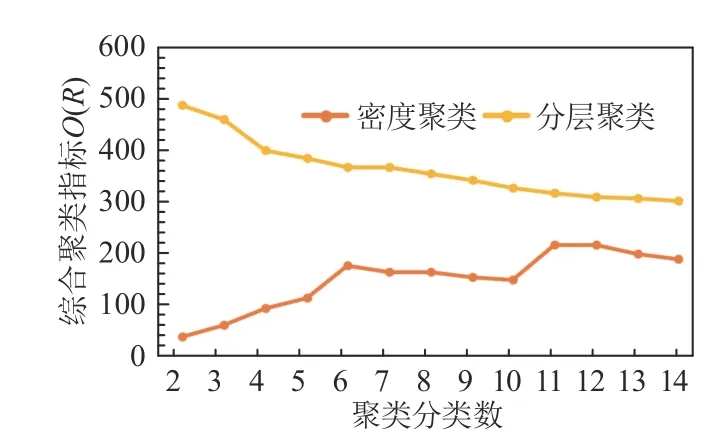
图9 综合聚类指标Fig. 9 Comprehensive clustering index

由图9 可知，当聚类分类数取为11 时，密度聚类算法的综合聚类指标O(R)取到最大值，其数值约为230，此时密度聚类算法的聚类效果最优。相比之下，本文所用的分层聚类算法综合聚类指标O(R)整体优于密度聚类算法，因此分层聚类算法聚类效果更优。另外，当聚类分类数取为2 时，分层聚类算法的综合聚类指标O(R)取到最大值，其数值约为500，因此本文取分类数为2 类。

为了更加清晰直观地展示分层聚类算法在不同分类别数下的聚类情况，本文分别以2、3、4、5 类别数为例展示场景分类，如图10 所示。从图10 可以看出，当取2 类别数时，已经呈现明显的聚类及其分界线。当取3 类别数时，虽然也呈现较为明显的分界线，但类别间的距离有所增加，因而综合聚类指标O(R)并不是最优。当类别数进一步增加时，例如4 类别数和5 类别数，此时类别间的界限逐渐模糊，甚至类别间出现部分交叉融合。

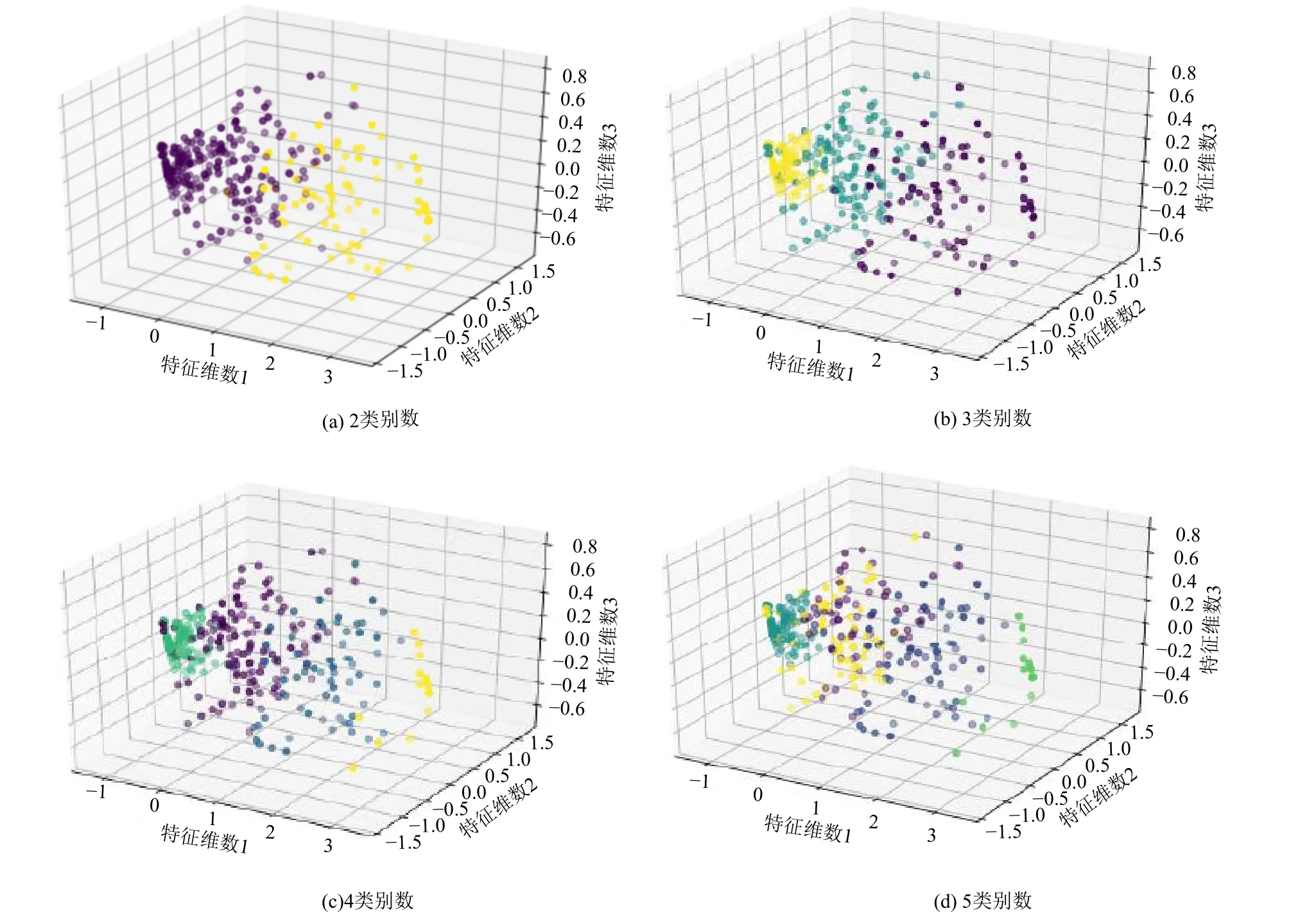
图10 不同场景类数下的分类结果Fig. 10 Classification results under different scenario classes

在2 分类数下，分层场景聚类算法所得到的代表性聚类场景如图11 所示，这2 个场景将代表风电出力场景嵌入联合系统双层运行优化模型中，以获得最优调度策略。

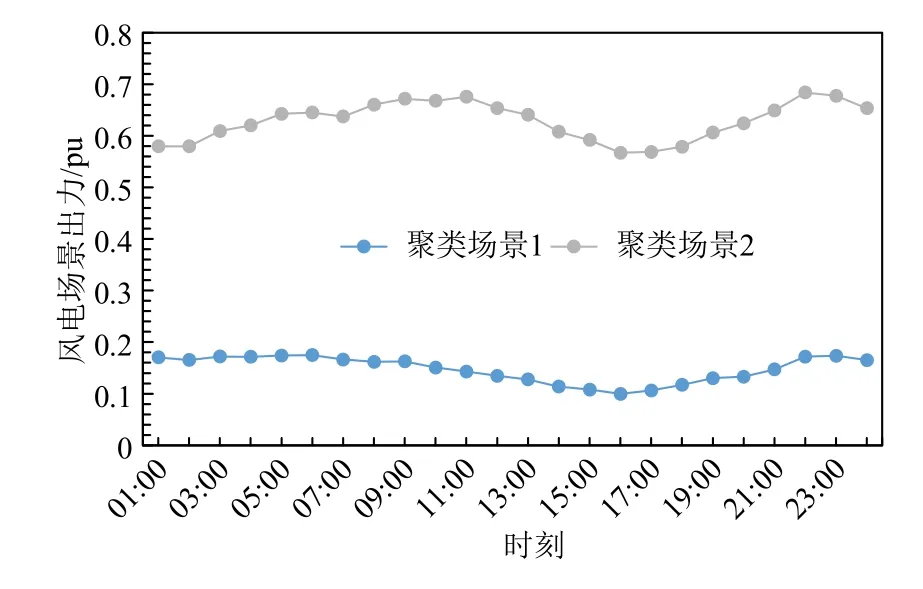
图11 分层聚类场景Fig. 11 Scenarios of hierarchical clusterings

5.2 调度结果对比

为了验证所提方法的有效性和优越性，本文将所提基于分层场景聚类的双层调度优化方法与确定性调度模型、经典随机优化调度模型对比，其调度出力如图12 所示，结果对比见表3。

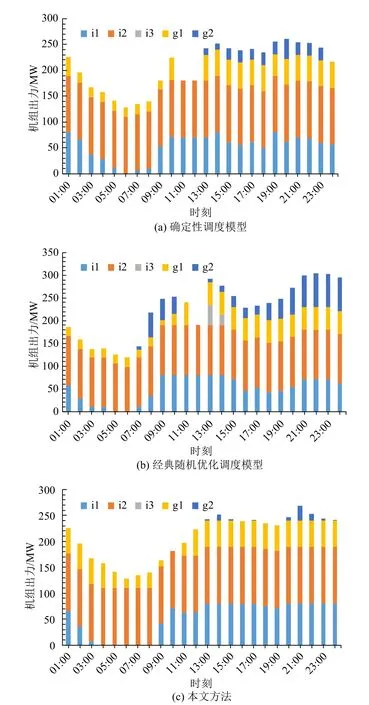
图12 发电机组发电功率Fig. 12 Generated output of generating sets

从表3 可看出，确定性调度方法假设可以得到准确的风电预测出力场景并对其进行优化，虽然日前运行成本最低，但由于其无法充分考虑风电不确定性和随机性，在风电波动严重时，将导致最多的切负荷和弃风，同时无法保证系统在风电波动最严重时的安全性。相比之下，本文所提的运行优化模型通过分层聚类方式考虑风电波动，在调度成本基本不变情况下，通过调整机组出力有效地应对风电波动场景，因而切负荷量和弃风量也显著减少。与经典随机优化运行模型相比，本文所提模型在总弃风切负荷量接近的情况下，大大地降低运行优化成本。综合而言，本文所提的方法可以在不明显增加运行成本的前提下，充分考虑风电不确定性，有效地减少切负荷量和弃风量，具有较强的工程应用价值。

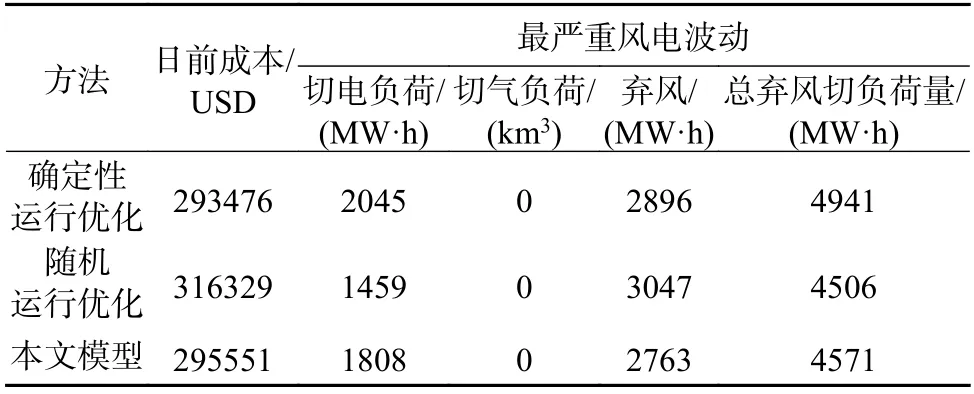
表3 不同调度方法的对比Table 3 Comparison of different scheduling methods

5.3 陡坡峰风况对调度策略的影响

需要注意的是，最严重的风电波动在实际中发生概率不大，更常见的是陡坡峰风况，即具有相邻时段具有较陡的风电波动。为了分析日常陡坡峰风况对确定性运行优化模型、随机运行优化模型和本文所建优化模型的影响，本文从西北风电数据中选取5 个典型陡坡峰风况场景进行分析，如图13 所示。在此5 个典型场景下各个调度模型策略所对应的切电负荷、切气负荷以及弃风量见表4。

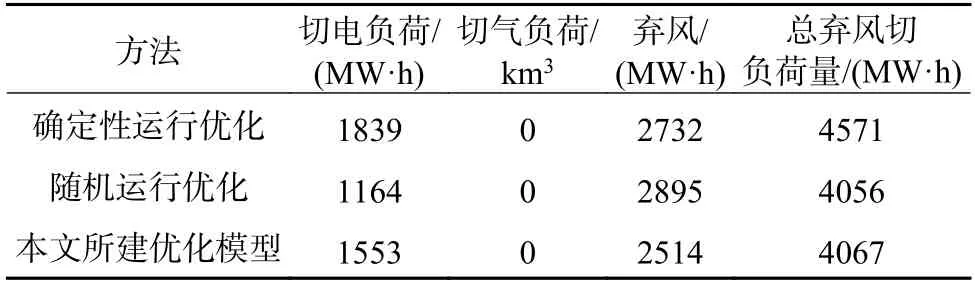
表4 陡坡峰风况下不同调度方法的对比Table 4 Comparison of different scheduling methods under peak wind conditions with steep slopes

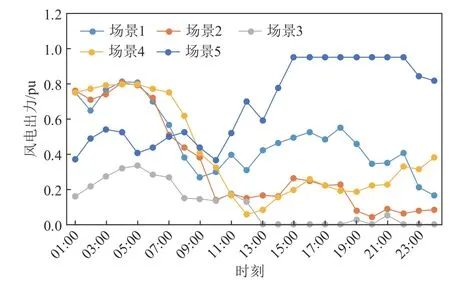
图13 典型陡坡峰风况场景Fig. 13 Typical peak wind scenarios with steep slopes

从表4 可看出，在陡坡峰风况下，与其他调度模型相比，确定性调度测策略所对应的切电/气负荷、弃风量均为最高，总弃风切负荷量较本文所建模型高11.03%；内嵌海量场景的经典随机运行优化模型由于其考虑了大量的风电波动场景，可以有效应对陡坡峰风况，所导致的切电/气负荷、弃风量最低。虽然本文所提模型的整体弃风、切负荷比经典随机运行优化模型稍高，但差异不明显，且本文所提模型所需场景远小于经典随机运行优化模型，因此在一定程度上验证了聚类场景的代表性以及所提运行优化模型的优越性。

5.4 不同风电渗透率下的结果对比

不同的风电接入容量会对最优调度策略产生不同影响。为了对比不同风电接入容量对所提调度优化模型的影响，本文定义风电渗透率为

从图14 可以看出，随着接入系统的风电渗透率不断升高，目标函数（即运行优化的总成本）逐渐上升，最后趋于稳定并稍微有所上升。这是由于在风电渗透率较低时，风电出力的占比较低，柴油机组、燃气机组等可控机组可以通过调节功率应对风电波动，因而总运行成本较低。然而，在可控机组容量不变的情况下，随着风电的不断接入，系统无法消纳多余的风电，因而造成更严重的弃风和切负荷，进而导致总运行成本逐渐增加。

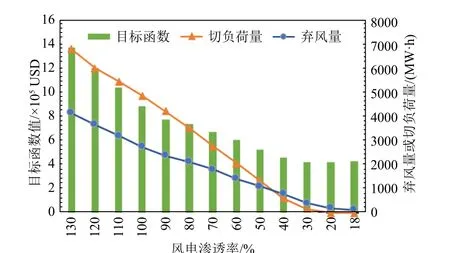
图14 不同风电渗透率下的指标对比Fig. 14 Comparison of indicators under different wind power permeability

需要指出的是，当风电渗透率低于某个阈值时，在本文算例中对应为30%左右，若再进一步降低风电渗透率，总运行成本将有所上升，这是由于在风电渗透率过低时，风电出力的占比极低，主要由需要消耗化石燃料的柴油机组、燃气机组提供电力，此时发电成本将逐渐上升，进而导致总运行成本增加。因此，在可控机组容量不变的情况下，该配电网−天然气耦合系统存在最佳的风电渗透率（约为30%）使得总运行成本最小，约为423559USD。

5.5 求解时间对比

为了进一步对比不同调度模型的计算性能，本文测试了不同风电渗透率下的CPU 计算时间，结果如表5 所示。在算法的相对求解精度设置为10−5时，由于经典随机优化方法在风电渗透率为40%～70%时计算时间超过15h 仍然无法得到最优解，因此为了得到可以对比结果，本文将算法的相对求解精度设置降低为10−4。

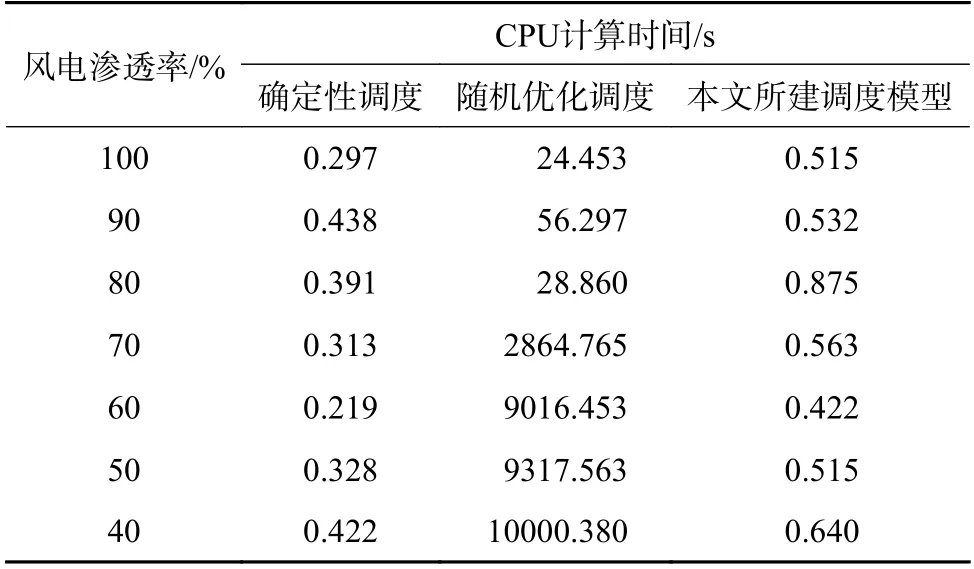
表5 不同调度方法的对比Table 5 Comparison of different scheduling methods

由表5 可知，经典随机优化调度模型由于通过大量场景的方式考虑风电不确定性，求解难度大大增加，平均求解时间超过4473 s，分别为确定性调度模型和本文模型的13002 倍和7712 倍，难以满足实际实时运行调度的需求。与之相比，基于准确风电出力预测场景的确定性调度模型计算时间最短，平均为0.344 s，而本文所提方法所需CPU 时间平均为0.580 s，与确定性模型较为接近，已可以满足日内实时调度要求，为考虑风电大规模接入联合系统的实时在线调度优化提供一种可行方法。

6 结论

为了合理考虑风电随机性的影响，本文从中长期、日前和实时3 个时间尺度，提出了考虑风电场景分层聚类的配电网和天然气网多时间尺度双层随机运行优化策略。算例表明：1）所用的分层聚类算法在各个聚类数情况下聚类性能均表现更优，同时所提的综合聚类指标可以有效地确定最优聚类数；2）本文所提模型在不明显增加运行成本的前提下，充分考虑风电不确定性，有效地减少切负荷量和弃风量；3）配电网−天然气网耦合系统存在最佳的风电接入渗透率；4）所提模型求解时间远短于经典随机优化调度方法，可满足实际调度的时间需求。