基于长短期记忆神经网络和改进型K-means聚类算法的居民峰谷时段划分模型

2021-12-20江兵李国荣孙赵盟庞宗强

现代电力 2021年6期

江兵，李国荣，孙赵盟，庞宗强

（南京邮电大学自动化学院，江苏省南京市 210023）

0 引言

峰谷分时电价作为一种常用的电力需求侧管理手段，通过充分发挥电价杠杆作用，促使用户采取合理的用电方式和用电结构，有利于实现电力负荷“削峰填谷”，提高电力系统稳定性及安全性[1-2]。

峰谷时段的划分是制定峰谷分时电价的基础，划分方法的结果直接影响用户的需求响应程度，从而影响分时电价的实施效果[3-5]。当前我国居民峰谷时段划分主要依据地区负荷的基本特征及工作人员的经验，缺乏相应的理论依据。因此，研究有效的居民峰谷时段划分模型具有十分重要的理论与现实意义[6-7]。

一个科学合理的居民峰谷时段划分模型应满足以下2 个特点：1）长期适用性。时段划分结果应在一个较长的时间范围内适用，如1 季度、半年、1 年等；2）差异性。同一时段负荷数据差异最小化，不同时段负荷数据差异最大化[5]。

当前国内外已有很多关于居民峰谷时段划分的方法。文献[8]采用半梯形隶属度方法对单个典型日的负荷曲线进行分析，通过判断时段所处高峰或低谷的概率来划分峰谷时段；文献[9]提出一种基于用户需求响应的峰谷时段划分方法，即在文献[8]方法基础上，对用户进行电价响应评估，通过评估结果调整峰谷时段划分属性，然而，文献[8-9]都仅考虑用户某一典型日的负荷曲线特点，无法保证时段划分结果的长期适用性；文献[10]提出一种以数据样本集高维化处理和K均值聚类分析相结合的时段划分模型，即对全年的用户负荷数据进行K 均值聚类，通过取平均值的方式获得最终的时段划分结果；文献[11]采用密度聚类的方法对全年带有时点信息的用户负荷数据进行聚类分析，将各时点的最大密度粒区间进行合并，最终形成峰谷时段划分结果。文献[10-11]虽然满足了时段划分的长期适用性和差异性原则，但对全年的每条用户负荷数据都进行聚类分析，将无疑增大算法的迭代次数以及模型实现的复杂程度，不具有很强的实用性。

为了解决传统峰谷时段划分方法因只选取单一典型日而无法在较长时间范围内适用的问题，提出一种基于长短期记忆神经网络（long short-term memory，LSTM）和改进型K-means 聚类算法（Kmeans clustering algorithm）的居民峰谷时段划分模型，利用LSTM 神经网络强大的长时间序列提取能力及改进型K-means 算法出色的聚类性能获得用户最终的时段划分结果。结果表明，相对于经典及当地的时段划分，所提方法的时段划分轮廓系数结果平均值更大，方差更小，更能反映居民用户实际的用电特点及用电规律，有利于挖掘用户侧需求响应潜力，获得更优的削峰填谷效果。

1 居民峰谷时段特性分析

1.1 用户负荷特点

居民用户的负荷具有较强的规律性及相似性，受到季节、日期类型、天气、经济发展水平等多种因素影响[12-13]。但由于居民的峰谷时段划分结果具有长期适用性的特点，需要根据往年的历史负荷数据情况进行长期分析判断，因此在考虑居民负荷影响因素时应选取每年固定且主要的部分。

通过研究发现，符合条件的居民用户负荷影响因素主要包含以下2 点：

1）季节。不同季节的负荷特性存在较大差异，春秋2 季温度适宜，负荷用量较少，夏冬2季由于过热或过冷，用户使用空调等调温设备，负荷用量较大。

2）日期类型。同一季节工作日和节假日负荷存在较大差异，居民在节假日的负荷用量较多，休息日的负荷用量较少，这跟用户在不同日期类型的用电习惯有很大关系。

因此，在对居民用户进行峰谷时段划分时，要充分考虑用户在不同季节和不同日期类型的用电特点和用电规律，才能使时段划分结果更符合用户的实际情况，更好地发挥分时电价的效果。

1.2 峰谷时段特点

如图1 所示，为某一典型日的居民用户负荷曲线分布情况，其中A 点为负荷曲线当日最小值点，B 点为负荷曲线当日最大值点，C 点为介于A、B 之间的某点。

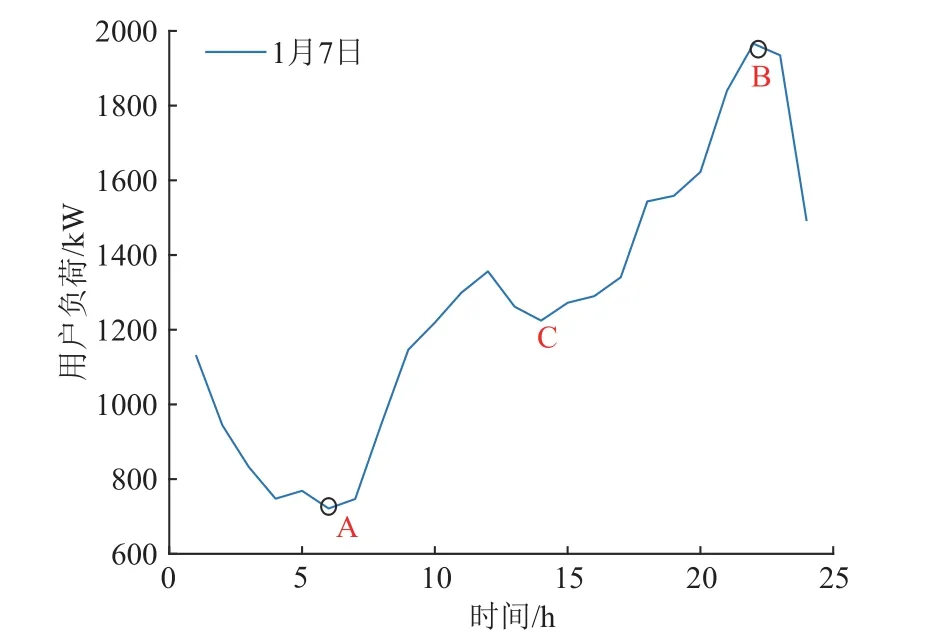
图1 某一典型日居民用户负荷曲线Fig. 1 Residential user’s load curve in a typical day

针对用户某一天的负荷曲线进行峰谷时段划分，基本原理是根据用户当天不同时段负荷的相对使用量来进行评判[10]。即将用户负荷使用量相对较多的时段划分为峰时段，负荷使用量相对较少的时段划分为谷时段，其余的划分为平时段。由图1 可以清楚地发现，最小值A 点一定属于谷时段的范围，最大值B 点一定处于峰时段的范围，且A、B 两点很接近谷、峰时段的中心位置[5]。

但是，在对用户较长一段时间（如1 季度、半年、1 年等）的负荷曲线进行时段划分时，如果仅仅利用某一典型日的划分结果来代表整段时间肯定是不合理的，这是因为用户每天的负荷曲线都会有一定差异，某一天的时段划分结果不能涵盖用户在这段时间内的所有用电信息。

理想的做法是将用户在这段时间所有的负荷数据都进行计算评判，然后选取出现最多的时段划分结果。但由于用户的负荷数据往往比较庞大且会存在一些极端情况，如停电等，传统的数学方法在解决该类问题时比较棘手。因此，本文引入数据挖掘算法中的长短期记忆神经网络算法（LSTM）以及改进型K-means 聚类算法，用以更好地解决居民用户峰谷时段划分问题。

2 居民峰谷时段划分模型

2.1 LSTM 原理

相较于传统的递归神经网络，LSTM 长短期记忆神经网络可以挖掘时间序列之间的隐含规律，解决传统循环神经网络（recurrent neural network，RNN）在训练时梯度消失的问题，使得这种特殊的RNN 网络具备强大的长时间序列特征提取能力[14-15]，很适合解决峰谷时段划分过程中居民负荷特征提取的问题。它的神经元结构如图2 所示。

图2 LSTM 神经元结构Fig. 2 Structure of LSTM neurons

每个LSTM 神经元内部由3 个门控单元组成，分别是遗忘门、输入门以及输出门[13]。

遗忘门决定上一时刻的单元状态有多少要保留到当前单元状态，它的计算公式如下：

其中：ft为遗忘门的输出结果；Wf为遗忘门的权重矩阵；bf为遗忘门的偏置量；ht−1为上一时刻神经元的输出结果；xt为当前时刻网络的输入值；[ht−1,xt]代表把ht−1和xt两个向量连接为一个向量；σ为Sigmoid 函数。

2.2 改进型K-means 聚类算法原理

K-means 作为常见的无监督学习聚类算法，在处理数值型且无标记的居民用户电力负荷数据方面有着出色的能力[16]。但它的缺点也是显而易见的，如K值的确定、初始聚类中心的选择等，都会影响聚类结果[17-20]。本文结合电力用户负荷的特性对K-means 算法进行一定程度的改进，以提高算法在电力负荷聚类中的效果。

K值的确定：当前我国大部分实行峰谷分时电价的地区将每天的时段划分为峰段、平段以及谷段，且取得了良好的效果，本文采用峰、平、谷3 段划分法，即K取值为3。

初始聚类中心的选择：根据本文1.2 节的研究内容，日负荷最大值有较大概率处于峰时段的中心，日负荷最小值有较大概率处于谷时段的中心，平时段的中心有较大概率处于峰谷中心的中间位置。因此，初始聚类中心选择为最小值点、最大值点以及中值点，用以加快聚类速度。

结合电力负荷特性的K-means 聚类步骤如下：

1）输入样本集S={x1,x2,···,xm}，m为样本的数量；聚类的簇数目3；最大迭代次数N；输出簇Ct=∅，t=1,2,3。

2）计算样本集中的最大值和最小值，并记录其出现的位置分别为a、b；计算a与b平均值的取整结果c，则初始的聚类中心µ={a,b,c}；

2.3 模型的建立

图3 为本文所构建的峰谷时段划分模型。模型的执行步骤如下。

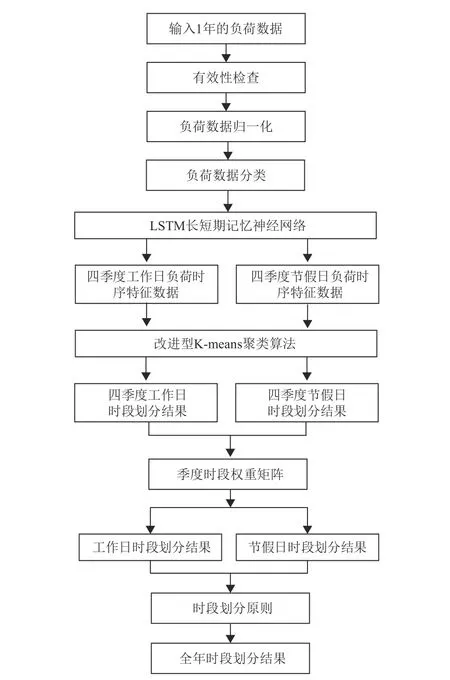
图3 峰谷时段划分模型Fig. 3 Peak and valley time division model

1）首先输入一年的负荷数据，对负荷数据进行有效性检查和归一化处理，确保数据的准确可靠，其中归一化公式如下：

2）根据本文1.1 节分析内容对负荷数据按照不同季节和不同日期类型分类，确保分类数据具有较强的相似性。

3）将分类后的数据共8 组分别加入LSTM进行训练，利用LSTM 神经网络强大的时间序列特征提取能力获得用户4 季度工作日及节假日的负荷特征数据。

4）将用户4 季度的工作日及节假日负荷特征数据分别用改进型K-means 算法进行聚类，输出用户4 季度工作日及节假日的时段划分结果。

5）由于各个季度的用电量有较大差异，因此应该在权重矩阵中得到体现。本文以各个季度中间月份的平均负荷作为依据，确定每个季度的权重系数，公式如下：

6）利用步骤5）计算得到的时段权重矩阵，将4 季度工作日及节假日负荷时段划分结果合并，获得全年的工作日和节假日时段划分结果。

7）通过模型计算出来的时段划分结果还应结合当前已实施时段划分方案的特点，以使模型的输出结果尽可能满足实际的情况，具体包括：

①要尽可能保证用户的总电费支出不要出现大的波动；峰段、谷段2 个集合的时段数相差不要太大，峰段可以尽量缩短，但不能低于6 h；

②不要出现短时间（低于2 h）的孤立时段，如果出现，将孤立时段合并到邻近平时段或谷时段；

③不能确定的时段按照少数服从多数原则进行合并。

2.4 模型的评估

模型最终输出居民用户的全年峰谷时段划分结果，其本质上属于数据挖掘中的聚类问题。因此使用聚类有效性指标来评估模型的最终输出结果。

聚类性能有效性指标主要分为2 种，即有监督评估指标和无监督评估指标。有监督指标需要用户负荷曲线的实际分类情况，由于居民用户负荷的灵活性，没有针对某个用户的标准分类，因此采用无监督指标作为评判的标准[14]。本文采用的是无监督指标中的轮廓系数Silhouette 指标，其公式如下

式中：mk为元素k与不包含该元素的集合中所有元素的平均距离；nk为元素k与所在集合中其他元素的平均距离；Sk是Silhouette 指标下元素k的计算结果，取值范围是[−1，1]，其值越大表明该元素更匹配所属集合而不与其他集合匹配，聚类效果更优。

为了表征某一天的时段划分结果是否合理，本文采用当天所有元素的平均Silhouette 结果作为度量的标准，其公式如下

3 算例仿真

为了验证本文建立峰谷时段划分模型的科学性与合理性，以江苏省常州某小区2200 户居民2017 年全年电力负荷数据为例，进行算例仿真。

首先对该小区居民用户一年的负荷数据进行有效性检查和归一化处理，并按不同季节和不同属性日分类，最终的负荷数据分类情况如附录A中的A1、A2 所示。

将分类后的用户负荷数据重组为1 维的时间序列分别加入LSTM 神经网络进行训练，网络的参数配置如表1 所示。

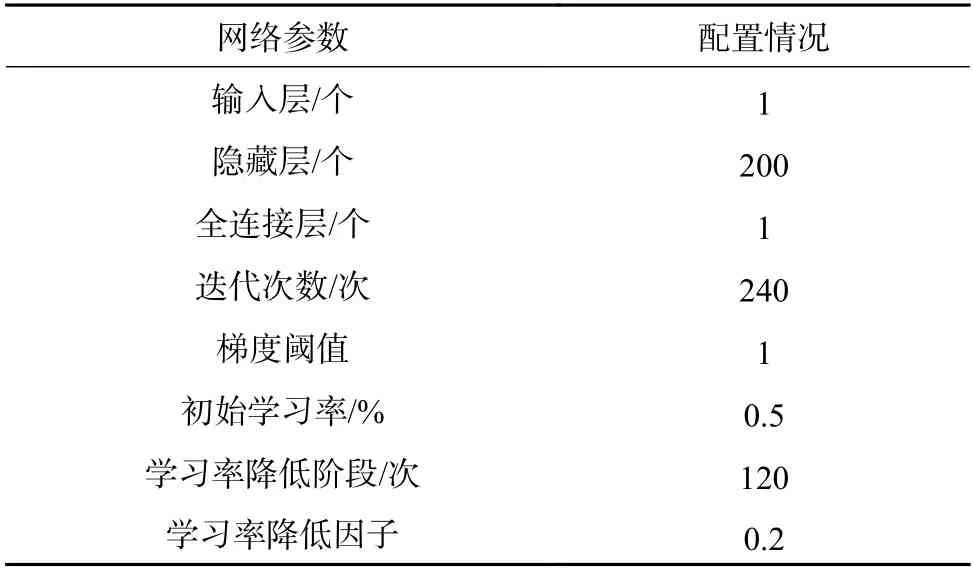
表1 LSTM 神经网络参数配置Table 1 Configuration of LSTM neural network parameters

使用训练好的LSTM 神经网络模型连续预测出24 时段的用户负荷数据，作为当前分类下用户的负荷特征数据。最终获得的居民用户4 季度工作日、节假日负荷特征曲线如图4 和图5 所示。

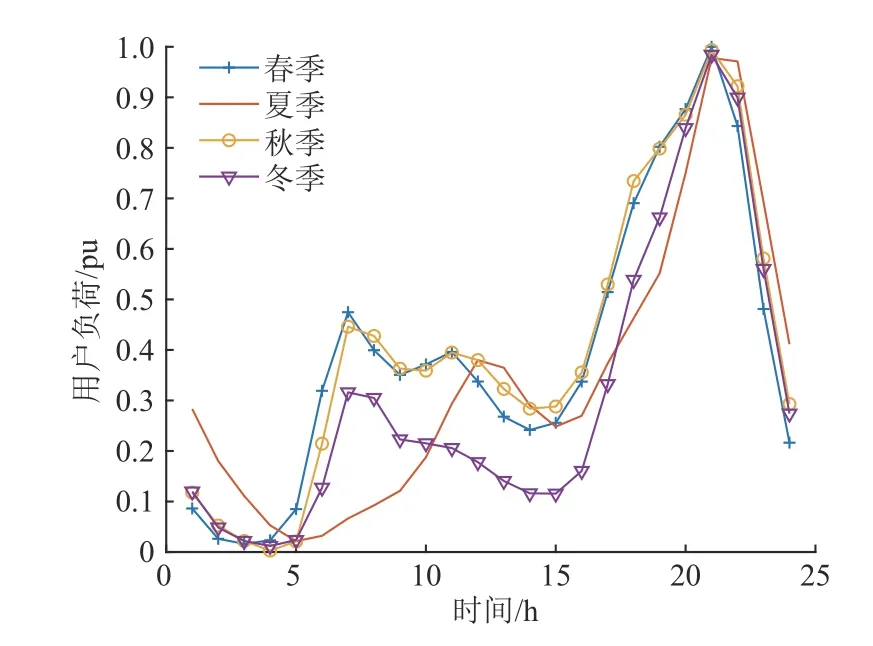
图4 4 季度工作日负荷特征曲线Fig. 4 Workday load characteristic curve in the fourth quarter

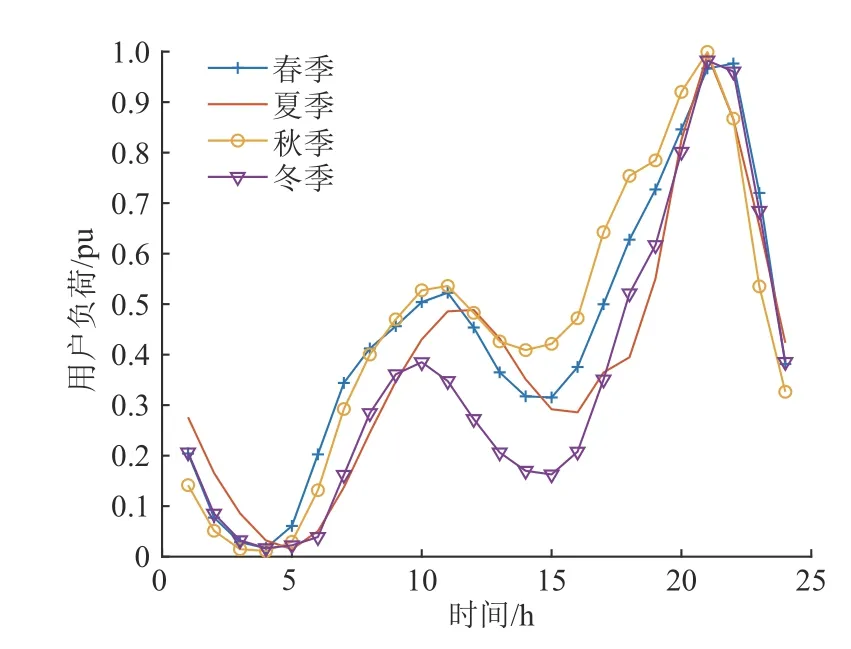
图5 4 季度节假日负荷特征曲线Fig. 5 Holiday load characteristic curve in the fourth quarter

分别对4 季度工作日及节假日负荷特征数据进行改进型K-means 聚类，时段划分结果如表2及表3 所示。

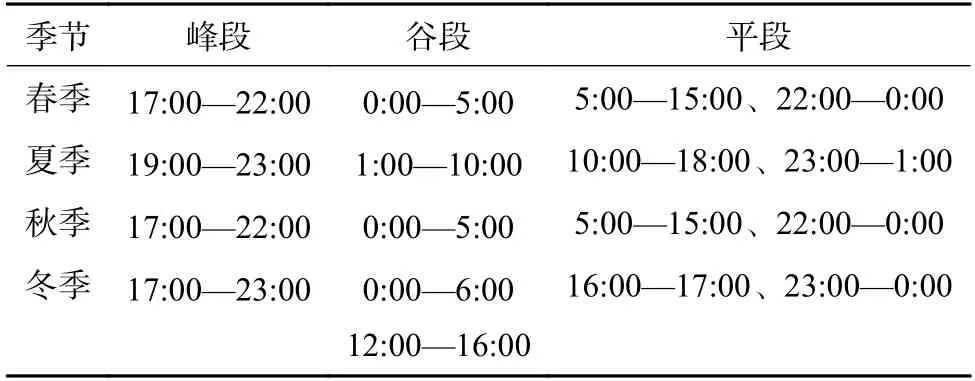
表2 全年工作日时段划分结果Table 2 Time interval division results of annual workday

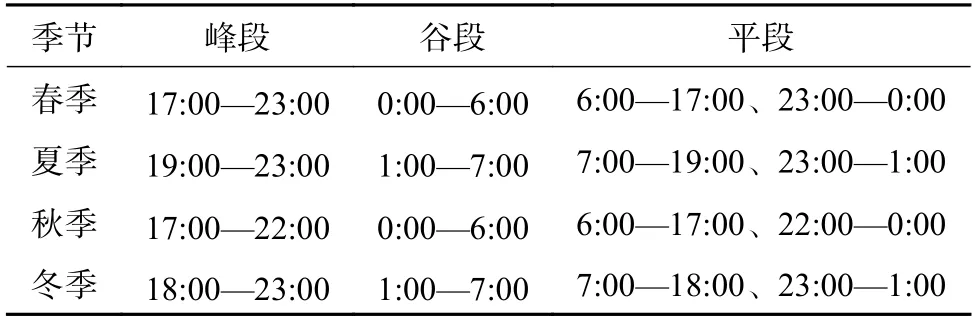
表3 全年节假日时段划分结果Table 3 Time interval division results of annual holiday

由表2 和表3 可知，春秋2 季在工作日、节假日的时段划分基本相同；夏冬2 季在工作日的谷段均有所延长，其中夏季的谷段是连续的，冬季的谷段分成2 个部分；4 个季节在节假日的时段划分比较相近，但存在一定的差异。为了充分考虑到4 季的差异性，分别计算各个季度中间月份（即4 月、7 月、10 月及1 月）的平均负荷作为4 季的权重系数，结果如下：

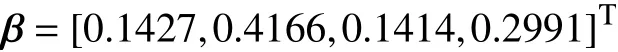
由计算结果可知，春秋2 季的平均负荷较为相近，夏季的平均负荷最高，其次是冬季。利用时段权重矩阵将全年工作日及节假日的结果合并，如表4 所示。

由表4 可知，与工作日时段划分结果相比，节假日的峰平谷时段都相应滞后1 h，这跟居民用户的用电习惯基本一致。根据时段划分原则对上述时段划分结果进行调整，获得用户最终的全年时段划分结果为：峰段(17:00—23:00)，共6 h；谷段(23:00—6:00)，共7 h；平段(6:00—17:00),共11 h。当地时间的时段划分结果为：峰段(8:00—21:00)，共13 h；谷段(21:00—次日8:00)，共11 h。2 者的时段划分对比如图6 所示。

表4 全年时段划分结果Table 4 Annual time interval division results

图6 时段划分方案对比Fig. 6 Comparison of time interval division schemes

如图6 所示，其中加号标记的阶梯线是本文方法的时段划分结果，包含峰、平、谷3 段；圆圈标记的阶梯线为当地的时段划分结果，包含峰、谷2 段；其余的8 条普通曲线是该小区4 季度工作日与节假日的负荷特征曲线，代表小区用户全年的负荷情况。通过曲线可以清楚地发现，在根据当地时间时段划分结果下(圆圈标记)，谷段的21:00—22:00 负荷值基本高于峰段全部负荷值，谷段的7:00—8:00 负荷值要高于部分峰段在14:00—15:00 的负荷值，而本文的时段划分结果(加号标记)出现类似不符合的情况较少，即本文的时段划分结果要优于当地的时段划分结果。

为了进一步验证本文模型的性能，采用经典的模糊半梯形隶属度时段划分方法对相同用户的负荷数据进行时段划分，结果为：峰段(19:00—0:00)，共5 h；谷段(0:00—6:00)，共6 h；平段(6:00—19:00)，共13 h。以该小区每月15 日的全天负荷作为测试数据，分别计算本文时段划分、经典时段划分及当地时段划分结果的轮廓系数Silhouette 值，如图7 所示。

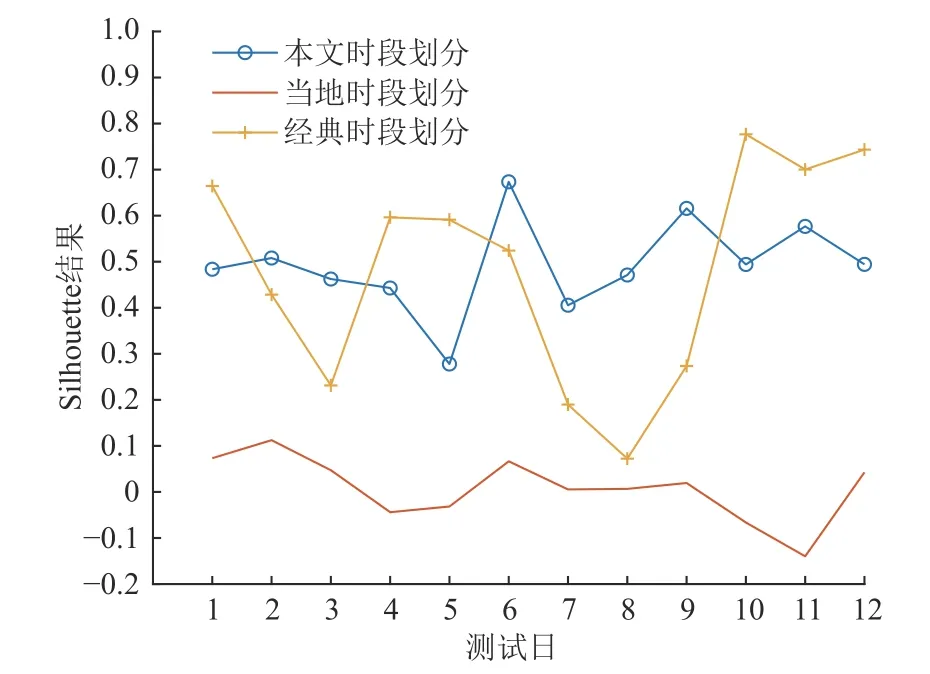
图7 不同时段划分的轮廓系数Silhouette 值对比Fig. 7 Comparison of the value of silhouette coefficients under different time interval division

由图7 可以看出，本文时段划分及经典时段划分结果的Silhouette 值均在0.5 左右上下波动，但经典时段划分的曲线波动比较明显，本文时段划分的曲线波动相对较缓，两者均在当地时段划分曲线之上。通过计算得出，本文时段划分、经典时段划分及当地时段划分的Silhouette 平均值分别为0.4921、0.4826、0.0077，方差分别为0.0103、0.0568、0.0048。相比之下，本文时段划分结果的平均值更大，方差更小，更能反映居民用户实际的用电特点及用电规律，有利于挖掘用户侧需求响应潜力，获得更优的削峰填谷效果。