宽体轻型客车行业的定性与定量销量预测研究

姜亚兰

（上汽集团南京依维柯汽车有限公司，江苏 南京 210009）

一、宽体轻型客车行业销量预测的窘境

宽体轻型客车行业的销量预测一直是行业内市场分析人员无法逾越的一座山。纵观近几年国家信息中心经济咨询中心在轻型车联合会上的报告，机构对于次年的市场容量的预测方法均以定性分析为主，做出对于趋势上升与下降的判断。谢国平2021年5月12日在轻型车联合会上发布名为《从商用车视角看“十四五”规划》的报告，通篇定性分析了规划对于轻型客车市场的影响，只字未提对市场容量进行定量预测。这些放之四海皆准的定性分析并不能让与会者清晰地看到市场未来的增量，各厂家只能雾里看花，彼此估量着对手的实力，并争夺存量市场。大家都迫切希望得到一个明确的数据：来年的蛋糕有多大？

二、宽体轻型客车市场的定性预测

在我国汽车行业，宽体轻型客车从属于商用车行业，指的是从事生产、服务或者被从事社会经济活动的单位、个体所持有的生产工具。近几年，随着宽体轻型客车行业产品技术的发展，产品种类进一步丰富，应用领域持续增加，个性化、高端化产品逐渐获得了更广或的应用空间。这使得宽体轻型客车的市场逐渐向产业链的下游延伸，越来越被个人用户所接受。因此，影响宽体轻型客车市场的因素也变得具有多样性。

从PESTEL模型角度分析，宽体轻型客车市场的变化主要受以下几个因素的影响。

政治方面：我国政治体制稳定，对宽体轻型客车市场的影响力度较小，但稳定的政治体制有利于任何一个行业的持续向好发展。

经济方面：2008年和2019年全球性的经济危机并未带给轻型客车市场较大的负面影响。恰恰相反，大量基础建设资金的投入，给宽体轻型客车作为生产工具这一用途带来了持续10年快速增长的窗口期。

社会方面：随着用户需求和倾向的多样化，产品也呈现出多样化发展的趋势。商用车虽然是生产工具，但在满足基础需求的前提下，对产品功能的兼容性、多元化提出了更高的要求，进而引起了车企对市场进行更加细致的分类。

科技方面：在基础科研层面，随着国内科研技术的发展，宽体轻型客车企业的研发技术不断提高，基于产品的工艺创新层出不穷，极大地丰富了产品的用途，将更多的个人终端用户纳入到了市场中，扩大了市场规模，为市场带了更多的增长动力。在前沿科技层面，由于新能源技术与互联网的发展，带来了汽车行业电动化、智能化、网联化、共享化的发展机遇，为商用车行业未来的增量指明了方向。

环境方面：节能环保的要求成为制约汽车行业发展的瓶颈。随着国家与用户环保意识的增强，市场更加容易接纳对环境友好的产品。

法律方面：首先，在较长一段时间的发展之后，宽体轻型客车行业的政策法规逐渐形成了一套中国标准，国家实施全产业链的质量与安全监管，倒逼企业进行持续的产品改进与技术创新。其次，在国家基于战略层面的考虑，在政策上释出汽车行业核心技术路线的变更意见，商用车行业将紧随乘用车的脚步，快速实现新能源技术路线产品的迭代更新。

综上所述，通过对于宽体轻型客车行业外部环境的分析可知，摆在车企面前的既有机遇也有挑战，既要争取增量市场，也不能放松对存量市场的研究。宽体轻型客车行业目前有三大驱动因素对市场容量的增长起到了正向影响：

一是国家层面对科研与技术开发资源的投入稳定增加，出台对于新技术产品的优惠政策，鼓励以企业为核心的技术进步。

二是宽体轻型客车产品应用的横向与纵向延伸。产品功能开发与市场需求互为依赖，相互促进，应用领域不断拓展：医药医疗、食品安全、农林牧渔、科学研究、军队武警以及许多民营领域都有较强的适应性。宽体轻型客车产品逐步延伸至产业链的下游，拓宽了增量市场。

三是进入宽体轻型客车行业车企与原有企业的竞争与合作促进了市场容量的扩张。2010年以前，宽体轻型客车行业内只有江铃汽车和南京依维柯两家车企，市场容量不足10万辆。2010年至2011年间，上汽、江淮、东风、福建奔驰纷纷进入市场；2015年福田图雅诺上市，取代了原有销量日益萎缩的福田风景，2021年上汽控股依维柯。虽然行业内进入车企众多，客观上带来了一部分市场的增量，同时也加剧行业内的存量竞争。

三、宽体轻型客车市场的定量预测

宽体轻型客车近几年销量呈现持续增长趋势，从公安部发布的上牌保险数据中看到：自2013年以来，宽体轻型客车的年市场容量就在10万辆以上，2018年突破15万辆，2020年达到19万辆。市场销量增幅每三年一个台阶，呈高位、低位、回归的态势。2010年至2020年的复合增长率为9.9%。

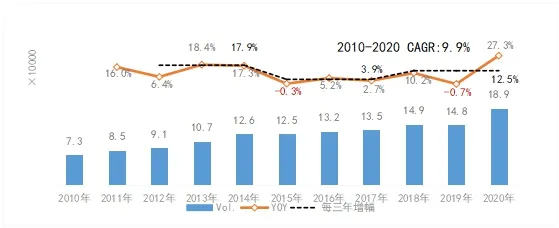
图1 2009年～2020年宽体轻型客车年度销量于同比走势

为了评估数据是否能够套用模型，必须先观察并计算该组数据的离散程度。

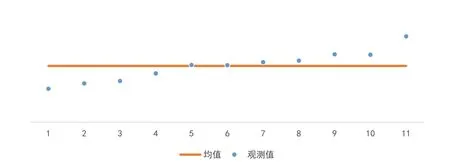
图2 2010年～2020年宽体轻型客车年度销量数据离散程度

从图表上看，2010年～2020年，宽体轻型客车市场销量数据是一组波动较小，具有较高稳定性的数值。总体均值为：123785；总体标准差：31750；离散系数：0.26。离散系数较小，数据的离群程度不高，说明数据间存在较强的规律。因此，我将利用数据序列模型和线性回归模型对这组数据进行拟合，用以预测后面一年的销量。

1.按照时间序列建立关系的定量预测模型

以2009年～2019年的数据为依据，预测2020年、2021年的市场容量，预测结果如表1所示。

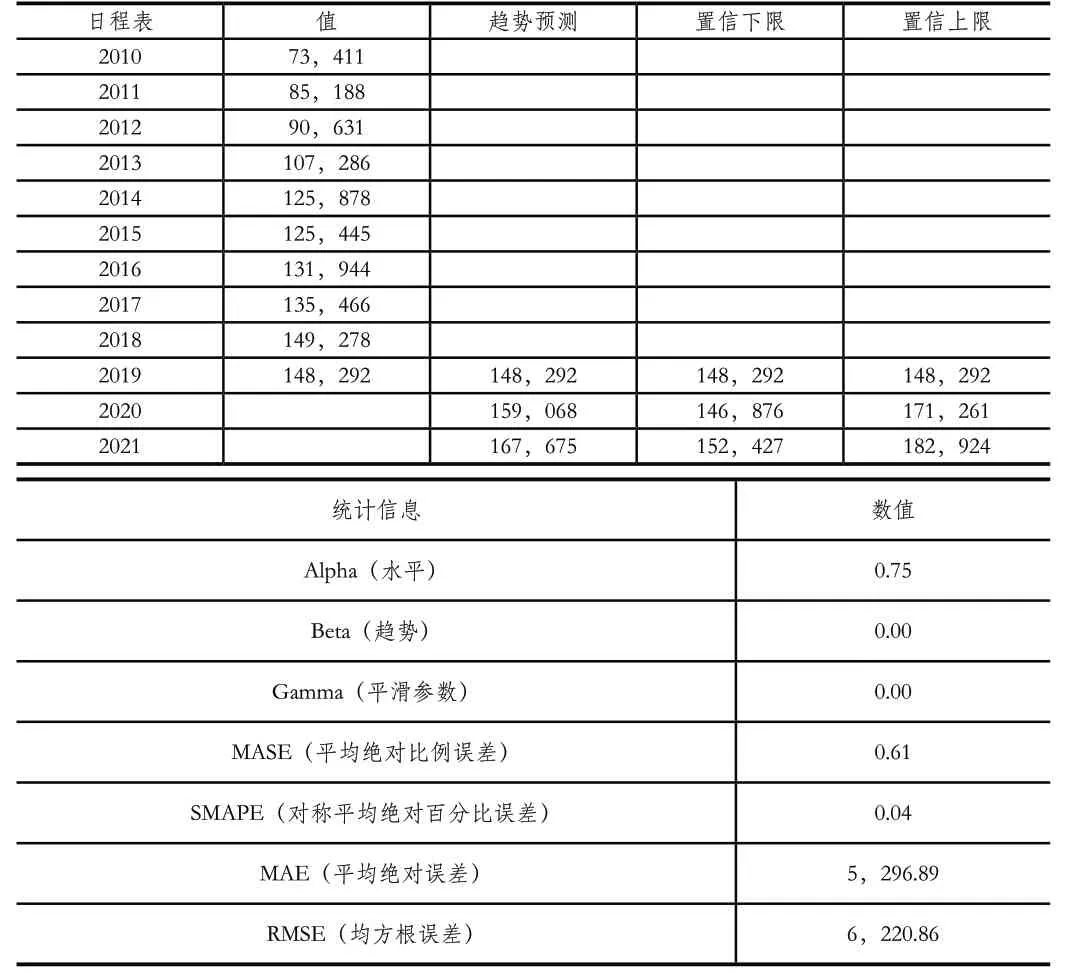
表1 时间序列模型预测值及数据组统计参数

对统计信息数值进行解读如下。

平滑系数：Alpha（水平）为0.75，beta（数据趋势）和gamma（平滑参数）参数等于0，显示这组数据非常平滑，模型的噪声小，预测数据有效性高。

错误指标：MASE（平均绝对比例误差）为0.61＜1；SMAPE（对称平均绝对百分比误差）为4%；表示误差足够小，预测模型有效。

MAE（平均绝对误差）、RMSE（均方根误差）均解释了模型计算拟合值与观测值之间的相差多大的数量。

预测结果如图3所示：2020年，宽体轻型客车市场容量在区间[14.7万辆-17.1万辆]内，区间中值为15.9万辆；2020年实际销量为18.9万辆，与预测上限相差1.8万辆，误差率9.3%；与预测中值相差近3万辆，误差率15.8%。

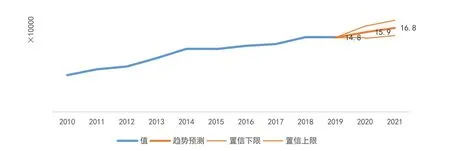
图3 时间序列模型预测2020年、2021年市场容量

2.按照回归模型进行定量预测

影响宽体轻型客车市场容量的指标有：国内生产总值（GDP）、城镇居民消费水平、全社会固定资产投资、工业生产者购进价格指数、第二产业增加值、货币供应量、消费品和原材料新订货单、制造业和商业存货账面价值变动等。

实际预测时，最常运用的是国内生产总值（GDP）。将GDP与宽体轻型客车市场容量建立相关关系，使用一元线性回归模型对次年的宽体轻型客车市场容量预测。为什么使用GDP作为唯一的经济指标建立线性回归模型？因为除了GDP以外，不论是先行指标还是同步指标都无法在当年做出较为准确的预测数值，因此也无法利用该预测数值与宽体轻型客车市场之间的相关关系来为次年的市场容量做出预测。

首先考虑GDP与宽体轻型客车市场容量两组数值之间的相关关系。

通过散点图图4可知：两组数据存在正相关关系，可以采用一元线性回归模型对数据进行拟合。

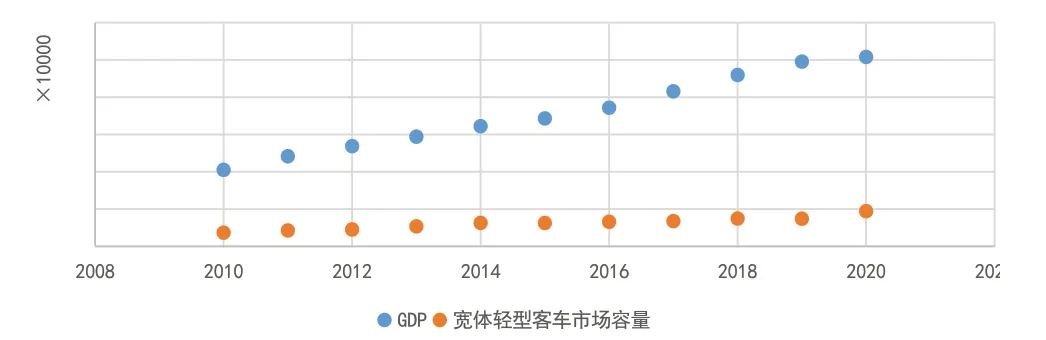
图4 GDP与宽体轻客市场两组数据分布状态

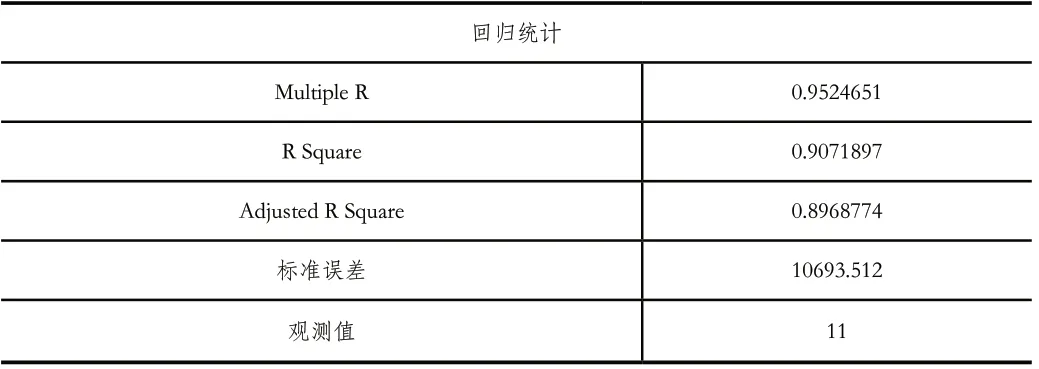
表2 回归模型对两组数据关系的统计值

Multiple R是相关系数，该值为0.95，是非接近于1，表面两组数据的相关性非常强。

R Square指模型拟合的精确度，越接近1，拟合程度越高。本次统计指标为0.91，说明模型的拟合精确度高。

Adjusted R Square是决定系数，是修正后的拟合系数。表示回归的平方和占总偏差平方和的比率，反映了自变量解释因变量变异的比率，其值越接近1说明回归的效果越好。虽然此次采用的是一元线性回归模型，模型的复杂程度不高，修正的R方参考意义不大，但该值接近0.9，再次印证了模型的拟合效果好。

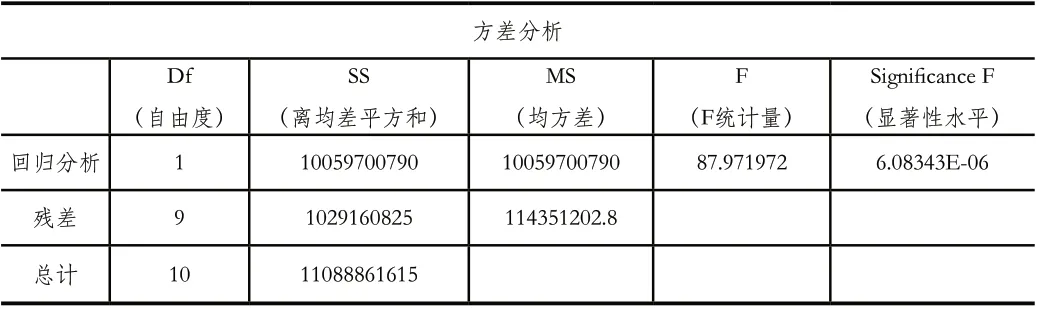
表3 回归模型中两组数据的方差分析

方差分析既变异数分析，用于对两个以及两个以上样本均值差别的显著性进行检验。

自由度解释的是变量的个数。

SS离均差平方和是指拟合值与观测值均值之间差的平方和。

MS均方差是误差平方和除以自由度的商。

F统计量是用来判断线性关系的。

Significance F说的是模型为假的概率。Significance F为6.08343E-06约为0.0006%，明显＜0.05，说明置信度达到了99.99%以上。

Coefficients列对应为模型的回归系数：截距α=13680.86；截距β=0.1543，既可建立回归模型。

P-value指的是参数的P值，作用同上表中Significance F值，说明置信度高达99.99%以上。

按照表4表达一元线性回归模型：Y=13680.86+0.1543X+ε，拟合图形如图5。

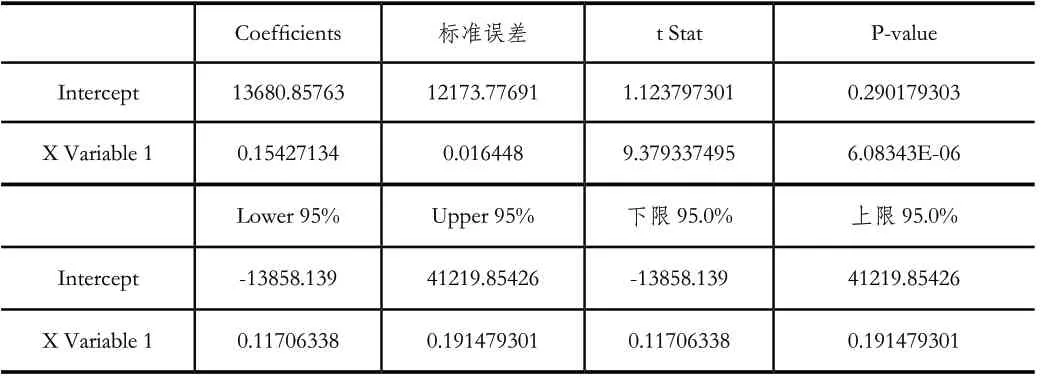
表4 回归模型参数及假设检验

图5 回归方程拟合值与观测值分布图

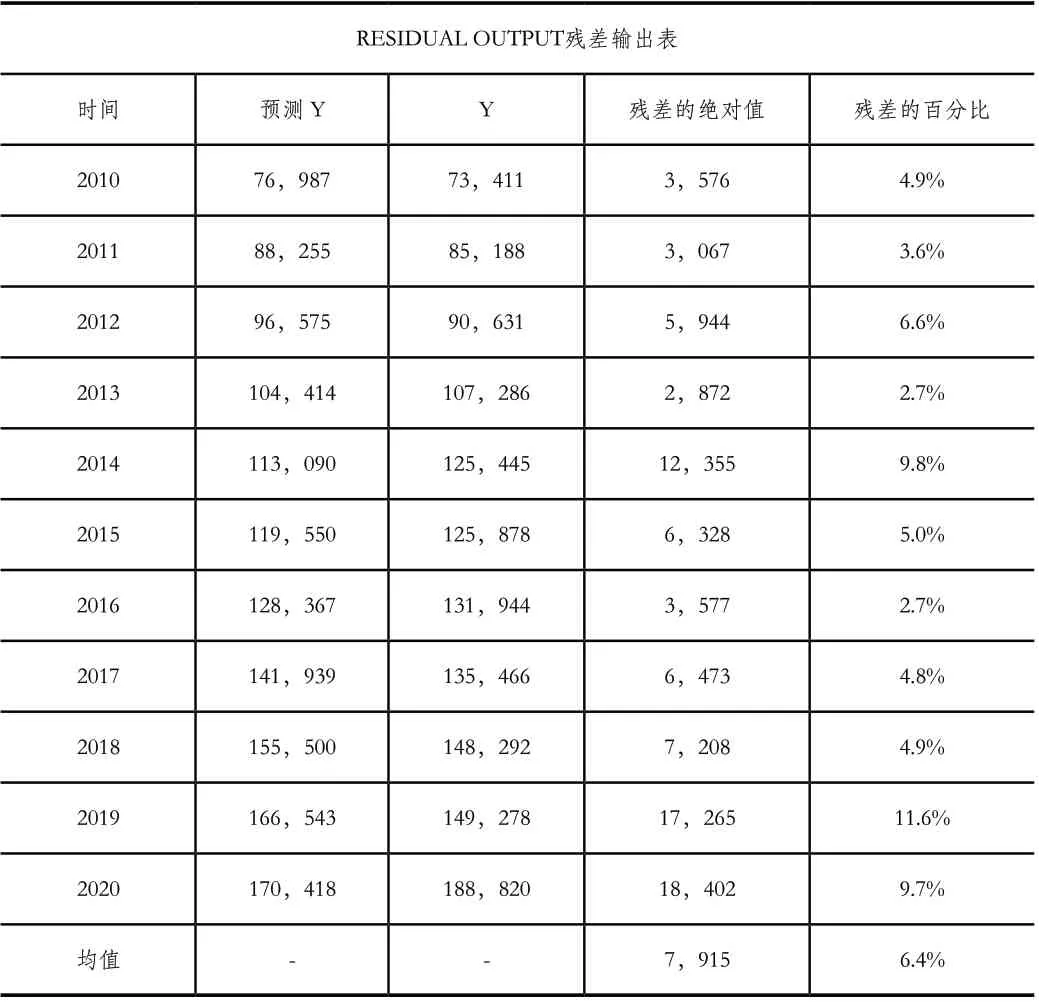
表5 回归方程拟合值与观测值的残差计算

从输出的结果看，以GDP为自变量来测算宽体轻型客车市场容量的一元线性回归方程拟合性较好。由方程Y=13680.86+0.1543X所测算出的宽体轻型客车预测值与实际值平均残差绝对值为7915辆，平均残差百分比为6.4%。残差的意义在于，当我们确定该一元线性回归方程的拟合性较好的情况下，拟合值与实际值之间差值相当于那些无法用数据量化的因素——环境因素对数值产生的影响。残差的百分比所展示的数值可以理解为环境因素对市场的影响力度。

3.两种定性预测方法的总结及实例分析

以上介绍了两种定性预测的方法，均对2020年宽体轻型客车的市场容量进行了预测。受新冠疫情影响，2020年国际国内环境变化剧烈，对于宽体轻型客车市场产生了巨大的影响。业内认为这是历年以来，外部环境因素宽体轻型客车对市场影响力度最大的一次，对于分析如何将定量预测与定性预测的数值结合，给出较为准确的市场销量预测结果具有典型的代表意义。因此，我将以2020年为例，我刚才分别用时间序列与一元线性回归方程对该年度的宽体轻型客车市场容量进行了预测，结果汇总如表6。

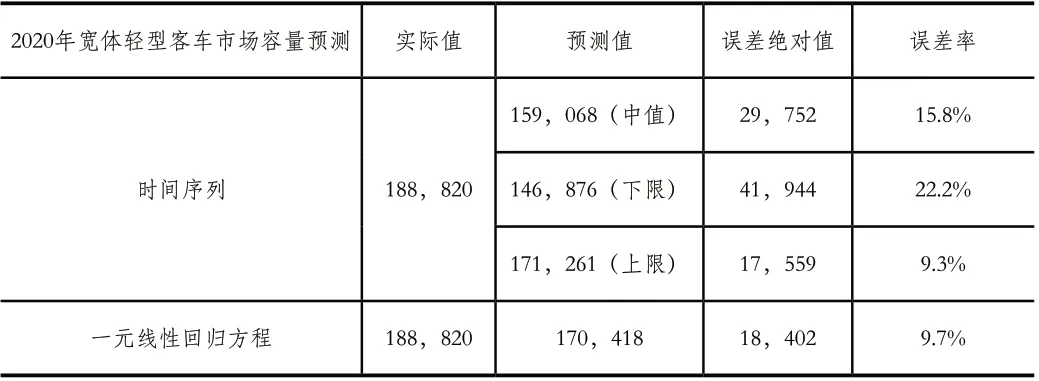
表6 两种模型预测值的误差评估

时间序列模型拟合的预测值（中值）与实际值之间相差近3万辆，误差率为15.8%，明显高于以GDP为自变量的一元线性回归方程所拟合的数值。因为2020年的GDP以及对预测值进行了一次修正。因此在其他条件不变的情况下，GDP对于宽体轻型客车市场销量的影响程度为：170418-159068=11350辆，影响程度为6.0%。

一元线性回归方程所拟合的预测值与实际值之间相差1.8万辆，误差率为9.7%，可以看出在其他条件不变的情况下，除了宏观经济的因素，还有部分行业因素对市场产生了影响。

对照2020年的分月销量可以看出，新冠疫情影响下的宽体轻型客车市场销量呈现前低后高的走势，如图6。

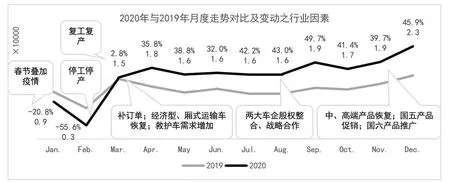
图6 新冠疫情对宽体轻客市场销量的影响

在此总结了一份当时影响销量的重大行业因素：

一月：春节与新冠疫情因素叠加导致的销售停滞，行业销量0.9万辆，同比下降20.8%。

二月：全行业停工停产导致的销售停滞，行业销量0.3万辆，行业内的排名第二、第三家主要车企月均销量不超过600辆。

三月：各单位陆续复工复产，销量恢至1.5万辆。由于救护车需求的爆发性增长，给整个行业来了1500辆的增量。

第二季度：头部省份的经济开始恢复，各车企陆续补足一月、二月被延迟的订单，满足M1类客车和厢式运输车的需求缺口。由于一季度经济停滞导致消费整个社会能力下降，经济型M1类产品替代了原消费者对中、高端产品的需求，给行业带来了1.1万辆的增量，49.8%的增幅。同时，依旧因为疫情，市场对救护车的需求持续增加，不仅为行业增加了2500多辆的增量，更在4月创造了单月销量历史最高点——1.8万辆，同比增幅35.8%。在行业政策方面：生态环境部、工业和信息化部、商务部、海关总署发布《关于调整轻型汽车国六排放标准实施有关要求的公告》，要求自2020年7月1日起，全国范围实施轻型汽车排放标准，禁止生产国五排放标准的轻型汽车。这份公告的发布导致汽油车销量结构增加了两个百分点。

第三季度：宏观经济的全面复苏让宽体轻型客车行业迎来了持续近一年的高速发展期。行业内的各车企均实现了市场的快速扩张。旅游业的复苏——尤其是一线城市的旅游业全面恢复——为商旅通勤市场实现3200辆，118.2%的增长。在本行业内：两家有股权关系的企业加快了战略合作的脚步。为了实现市场的互补性合作，这两家车企在各自擅长的领域加大了技术推广与促销力度，在市场占比最大的经济型市场、专用改装市场均实现了快速增长。由于客货两用市场持续保持增长、商旅通勤、物流运输以及专用改装市场又为整个行业注入了新动能，在四重因素叠加的影响下，9月份再次创下了行业单月销量新高——1.9万辆。

第四季度：宏观经济环境欣欣向荣，购买力的回归导致中、高端产品比例恢复至41.1%，宽体轻型客车市场依旧保持高速增长。在行业政策方面，离实施重型柴油车的国六排放的时间还有9个月，直至12月底，国六车辆的销量占比提高至40%。各车企在推进国六产品下沉的同时开始加快消化国五车辆的社会库存，各种商务政策的力度也相应加大。各车企的相继促销直接将行业12月的零售销量推至2.3万辆的历史最高位。

总结2020年定性影响因素主要是：意外情况——新冠疫情导致3个月的生产销售停滞、救护车及专用车市场需求增加、商旅通勤产品报复性增长、加快物流行业发展扩张；行业政策——排放升级推动经济型产品促销与中高端市场的回归；车企行为——行业中两家车企进行深度战略合作。

四、结论

将上述方法运用到对于2021年的市场预测中去。由时间序列模型判断，2021年宽体轻型客车市场大概率依然为增长趋势，去年的因素依旧会影响本年度的市场需求。下半年是否还有其他定性因素将会对行业产生影响尚且不得而知。但我们依旧可以从一元线性回归方程来为今年的销量做一个大体的判断。在宏观环境保持不变的情况下，IMF对今年中国的GDP增长预测为8.1%。带入方程Y=1368.86+0.1543X计算Y=13680.86+0.1543×（1+8.1%）×1015986.2=183145.63≈18.3万辆。根据上一段的分析，2021年与2020年有着同样的定性因素，所以要在基础预测值的基础上加上相同的误差值1.8万辆，预计销量为20.1万辆。

最后，对于宽体轻型客车市场销量的预测，首先对于次年的市场走势做出增长或下行的判断，然后将权威机构对于GDP的预测带入一元线性回归方程中，计算出基础定量预测值，最后研究对行业可能产生影响的定量因素，在基础定量预测值的基础上增加或减少5%～15%的误差值。