用联想之法破思考之困

林宏

摘要：在初中数学知识学习中，几何是比较重要的知识，也是比较难写的知识点，其具有一定的抽象性，学生在学习过程中，通常会比较的迷茫，不知道怎样去解几何题。但是，在几何教学中，加强联想方法的应用，则可以有效提升学生解题的难度，提高学生的逻辑思维，形成一种联想思维学习方法，进而帮助学方生突破几何学习的困境。基于此，文章对初中数学几何教学中联想方法的应用开展了深入的探究和探索。

关键词：联想法;初中数学;几何教学

中图分类号：A  文献标识码：A  文章编号：（2021）-45-438

1.联想教学内涵

联想教学方法，是人们通过想象想起其他相关的事物和人。在教学过程中，联想教学方法，是在初中数学几何教学过程中，教师通过引导学生读图和读题，使其抓住几何题中的一些关键的信息，然后开展联想，通过顺向、逆向、以及关联联想，将基本知识、方法和模型与几何问题相联系，进而帮助学生破解审题、思路等思考困难。

在联想教学中，通过联想“三部曲”来帮助学生破解思考之困，主要是通过顺向、逆向和关联联想来解决几何问题。顺向联想，是基于条件开展联想，其要解决的是“怎样去想”的问题，是指从己知条件出发，顺向联想所学过的几何定义、性质等基本知识，以此来破解审题之困。而逆向联想，是基于结论开展逆向联想，要解决的是“怎样分析”的问题，是指从结论出发，逆向联想所学过的算法、证法等基本方法，以此来破解思路之困。关联联想，是基于模型开展联想，要解决的是“怎样化归”的问题，是指从题目出发，关联联想所学过的静态模型和动态模型，将陌生问题变位熟悉问题，将未知转为已知，以此来破解添线之困。

2.初中数学几何教学中，联想方法应用策略

2.1基于条件的顺向联想，利用基本知识，破审题之困

在初中几何学习过程中，学生经常会出现拿到题目不知道“怎样去想”的情形，所以在几何教学时我们可尝试引导学生从己知条件出发，顺向联想所学过的几何定义、性质等基本知识，以此来破解学生的审题之困。

例如：如图1，在四边形ABDC中，∠ABC=∠ADC=90°，点E、F分别是AC、BD中点。判断与EF与BD的位置关系，并说明理由。

这是八年级上册直角三角形书后作业改编题，属于几何基础题，但还是有相当一部分学生思路无法形成。教学过程中，教师若能从己知条件出发引导学生进行顺向联想，也许会取得事半功倍的效果.从己知条件∠ABC=∠ADC=90°，点E、F分别是AC、BD中点，结合直角三角形斜边上的中线等于斜边的-半，就会联想到图2，由此连结BF、DE、，在得出BE=DE后引導观察EF、BD的位置，进而就容易联想到得要三角形三线合一这个知识点如图3，由此问题得以解决。

2.2基于结论的逆向联想，利用基本方法，破思路之困

逆向联想，是根据实物的一些实践顺序或者观念逻辑顺序，通过后面的事物联想到另一事物[1]。这种方式的联想，在一定程度上充分认识事物间的关系，同时也是检验推理是不是正确的重要依据。

在初中几何学习过程中，学生经常会出现拿到题目不知道“怎样分析”的情形，所以在几何时我们可尝试引导学生从结论出发，逆向联想所学过的算法、证法等基本方法，以此来破解学生的思路之困。

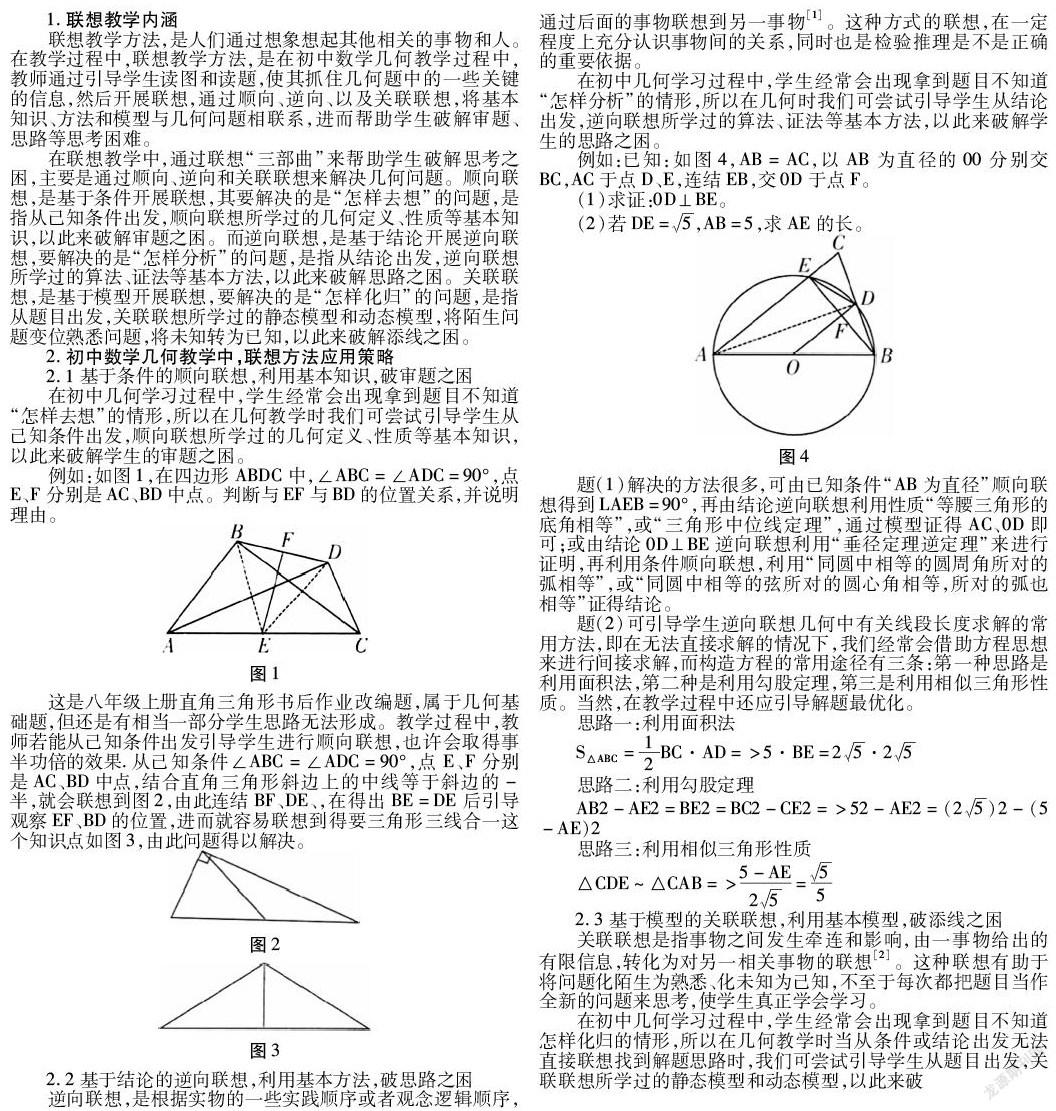
例如：已知：如图4，AB=AC，以AB为直径的00分别交BC，AC于点D、E，连结EB，交0D于点F。

（1）求证：0D⊥BE。

（2）若DE=5，AB=5，求AE的长。

题（1）解决的方法很多，可由已知条件“AB为直径”顺向联想得到LAEB=90°，再由结论逆向联想利用性质“等腰三角形的底角相等”，或“三角形中位线定理”，通过模型证得AC、0D即可;或由结论0D⊥BE逆向联想利用“垂径定理逆定理”来进行证明，再利用条件顺向联想，利用“同圆中相等的圆周角所对的弧相等”，或“同圆中相等的弦所对的圆心角相等，所对的弧也相等”证得结论。

题（2）可引导学生逆向联想几何中有关线段长度求解的常用方法，即在无法直接求解的情况下，我们经常会借助方程思想来进行间接求解，而构造方程的常用途径有三条：第一种思路是利用面积法，第二种是利用勾股定理，第三是利用相似三角形性质。当然，在教学过程中还应引导解题最优化。

思路一：利用面积法

S△ABC=12BC·AD=>5·BE=25·25

思路二：利用勾股定理

AB2-AE2=BE2=BC2-CE2=>52-AE2=（25）2-（5-AE）2

思路三：利用相似三角形性质

△CDE～△CAB=>5-AE25=55

2.3基于模型的关联联想，利用基本模型，破添线之困

关联联想是指事物之间发生牵连和影响，由一事物给出的有限信息，转化为对另一相关事物的联想[2]。这种联想有助于将问题化陌生为熟悉、化未知为己知，不至于每次都把题目当作全新的问题来思考，使学生真正学会学习。

在初中几何学习过程中，学生经常会出现拿到题目不知道怎样化归的情形，所以在几何教学时当从条件或结论出发无法直接联想找到解题思路时，我们可尝试引导学生从题目出发，关联联想所学过的静态模型和动态模型，以此来破解学生的添线之困。文章中提到的数学模型，主要是将特定问题和特定事物的数学结构给反映出来。

例如：如图5，在四边形ABCD中，∠ABC=CADC=∠ACD=45°，BC=2，AB=5，则BD等于（  ）.

这是一道几何综合性问题，很多学生拿到之后会无从下手，事实上，我们只需抓住题干或图形中的关键信息，适当展开静态模型相关的联想很快就能找到解题思路。

比如，根据“等腰Rt△ABC”条件和图形位置特点，引导学生关联联想“旋转形”（图6），可将△ABC以A为旋转中心，逆时针方向旋转90°（图7）或将△ABD以A为旋转中心，顺时针方向旋转90°（图8），求出相关线段长度后借助Rt△BDE或Rt△BCF即可求得答案。

这道试题的总体思路是通过构造直角三角形，利用勾股定理求出BD的长度。

结语

综上所述，在初中数学几何教学中，教师要对联想教学方法重视起来，加强其在几何教学中的应用，引导学生通过联想，破思考之困，提高学生的数学解题能力，同时也提高了初中数学课堂教学的高效性。

参考文献

[1]段雄东，黄慧，马丹.条件联想审题在初中几何题中的运用[J].读与写，2020，17（30）：171.

[2]唐双利.初中数学教学中学生联想思维能力的培养[J].师道·教研，2012（11）：47-47.