发现学习 自主建构 提升素养——以“平面与平面垂直的性质定理”为例

王 娜 (江苏省苏州工业园区星海实验中学 215124)

与传统的学习形式相比，发现学习注重建构而不是接受，主张以小组为单位，团队合作，以探究作为主要方式，让学生亲自参与所学知识体系的建构，自主发现，自主成长．学生能够领悟定理教学中所蕴含的数学思想方法，形成理解和分析问题的学科思维能力是数学核心素养形成的最高表现．[1]因此，数学定理的教学要以学生为本，在教师的引导下开展发现学习，在创造、建构、合作、发现的过程中，培养直觉思维和内在机制，提升学生的数学核心素养．

笔者于2021年5月参加了苏州市高中数学优质课的比赛，课题为人教A版“8.6.3 面面垂直的性质定理”(第一课时)．下面以发现学习为导引，呈现本节课的教学过程．

1 教学内容简介

“平面与平面垂直的性质定理”是人教A版第八章第六节中的内容，是直线与平面位置关系中的最后一节．此时，学生的知识积累、解决问题的方法都较为丰富，所以本节内容充分类比直线与平面垂直性质定理的研究方法，借助创设的辅助线和面，通过特殊位置关系的研究获取性质定理和结论．本节课的重点是平面与平面垂直性质定理的发现与探索过程，难点是研究图形几何性质的一般思路和方法．

2 教学内容预设

本节课设置了学生感兴趣的生活情境——《山河令》主题演唱会的舞台实景图片，让学生直观感知情境中所蕴含的数学问题，通过小组合作研究，抽象出数学模型，提出猜想并严谨论证，培养学生自主探究、团队合作的能力．类比直线与平面垂直性质定理的研究方法，通过直观感知、操作确认、推理证明，获得平面与平面垂直的性质定理，享受由具体实例的直观感受与逻辑推理的严谨论证所带来的数学之美．

3 教学过程

3.1 设置情境——复习中引入

问题1前面我们学习了线面垂直的性质定理，即垂直于同一平面的两条直线平行．我们是如何研究线面垂直的性质的？

生：在线面垂直的条件下，去寻找新的命题．我们添加了新元素(线和面)，新元素与已知的线面具备特殊的位置关系，比如线在面内、线在面外、平行、垂直等，由此获得了性质定理和结论．

师：很好，以上就是线面垂直性质的探究方法．

设计意图复习直线与平面垂直的性质的研究过程，强化研究方法，让学生体会研究线面的平行、垂直的判定定理与性质定理，就是研究元素由少到多、由简单到复杂的过程．类比研究的过程和方法，为学生探究面面垂直的性质做好铺垫．

问题2上节课我们已经学习了面面垂直的判定定理，那么在两个平面互相垂直的条件下，我们又可以研究哪些性质？

设计意图学生通过前面七个定理的探究与学习，具备了一定的数学素养，故本节课采用小组讨论、合作研究的方式：研究的对象由学生提出，内容由学生发现，方法由学生讨论，使其经历“直观感知、操作确认、推理证明”的历程．

3.2 知识构建——合作中生成

教师展示几幅图片，看看这几幅图片能否给学生带来一些启示．

师：刚刚结束的五一小长假期间，我们苏州热度最高的当属“《山河令》主题演唱会”．图2、图3就是演唱会现场的舞台实景．请同学们结合图片看看这对我们研究面面垂直的性质带来哪些启示．

图1

图2 图3

(以小组为单位，相互协作，合作探究．此时课堂气氛活跃．之后由小组代表展示成果．)

设计意图从学生感兴趣的话题切入，使其体会舞台实景中蕴含的数学问题．突出发现与体验，培养学生直观想象、数学抽象等素养．

小组1成果展示：

生：我首先发现了地面与舞台背景面垂直，而在背景面射出的灯光有水平的、斜着的、竖直的，那么就可以把地面和背景面抽象成两个互相垂直的平面，把灯光抽象成直线．

师：你能将上述问题抽象为数学问题吗？

生：如果两个平面α和β互相垂直，直线b在平面β内，那么它与另一个平面α会有怎样的位置关系？

生：我们小组共画出了四种情况，所以我们觉得可以分成四类：图4，b⊂α；图5，b∥α；图6，b与α相交；图7，应该是垂直．

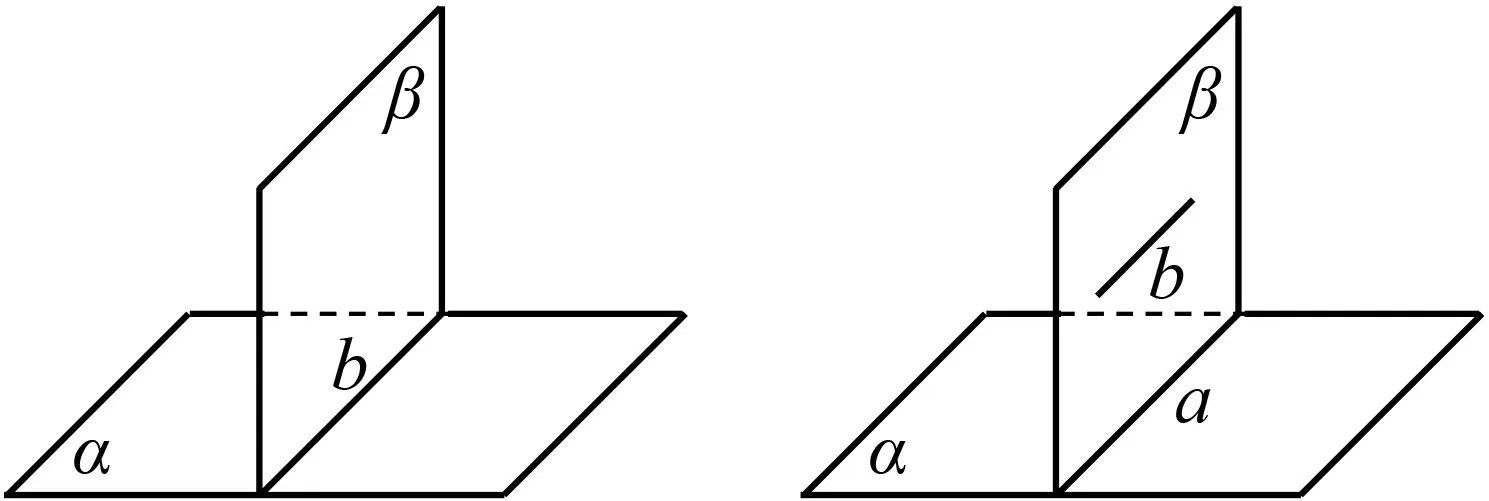
图4 图5

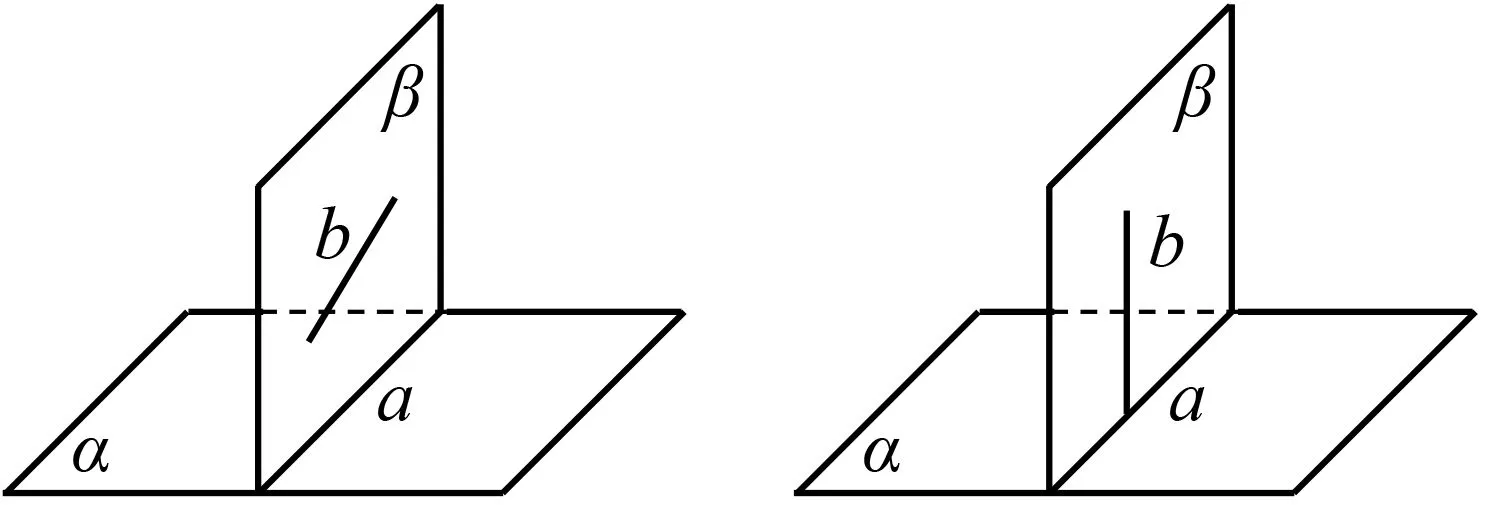
图6 图7

师(追问)：两个平面垂直，当直线b满足什么条件时可以得到特殊的位置关系？

生：图5，b∥a，可证b∥α；图7，b⊥a，猜想b⊥α．

师：那么我们就可以猜想，两个平面垂直，如果一个平面内有一直线垂直于这两个平面的交线，那么这条直线与另一个平面垂直．

设计意图课堂展示的过程是学生感知发现、抽象猜想的过程．通过小组交流，组内成员共享经验，抽象出数学问题，并提出猜想．这一过程体现了“直观感知、操作确认”在发现图形位置关系中的作用，有利于提升学生数学抽象、直观想象等数学素养．

师(追问)：猜想的条件和结论分别是什么？能否用符号语言表示出来？能否证明？

以小组为单位继续讨论，教师巡视，之后投影学生的书写过程并由学生讲解自己的思路．

条件：α⊥β，α∩β=a，b⊂β，b⊥a．结论：b⊥α．

生：要证线面垂直，就要找到面内的两条相交直线与已知直线垂直，而b⊥a，故只要再找到一条直线与b垂直即可．再联想到条件α⊥β，由面面垂直的定义可以知道二面角的平面角为直角，所以就想到要去构造二面角的平面角，即在两个半平面内分别作棱a的垂线，这样就构造出了一条直线与b垂直，于是得到了线面垂直．

设计意图在学生提出猜想后，引导其将猜想的条件和结论用符号语言表示出来，为面面垂直的性质定理作好铺垫，再通过小组讨论，合作探究，整理证明过程，并由学生讲解自己的证明思路，提高其表达能力和抽象概括能力．

师：非常好！小组1的同学借助背景面中不同方向的光线，研究出与地面的位置关系．从实际模型中抽象出具体的数学问题，猜想后给出了严谨的论证(此时教室里响起了掌声)．这就是平面与平面垂直的性质定理，请同学们分别用文字语言、图形语言、符号语言来表示．

设计意图通过三种语言的转换，帮助学生更好地理解性质定理，培养抽象概括的能力．

(板书)用三种语言表示平面与平面垂直的性质定理．

小组2成果展示：

生：性质定理中，在一个平面内作交线的垂线，垂直于另一个平面.我们小组想问：如果背景面中射出的光线垂直于地面，该光线是否一定在背景面中？也就是说，经过一个平面内的一个点作另一个平面的垂线，是否在第一个平面内？

师：你能将上述问题抽象为数学问题吗？

生：如果两个平面α和β互相垂直，对于平面α内的点P，如果过点P向平面β作垂线a，那么直线a与点P所在的平面α有什么位置关系？

猜想：如果两个平面垂直，那么经过第一个平面内的一点作垂直于第二个平面的直线，该直线在第一个平面内．

师(追问)：猜想的条件和结论分别是什么？能否用符号语言表示出来？能否证明？

设计意图类比性质定理的研究历程，结合图形(图8、图9)，把猜想的条件和结论用符号表示出来，强化三种语言的相互转化，再通过小组合作探究，培养学生严谨的逻辑思维能力．

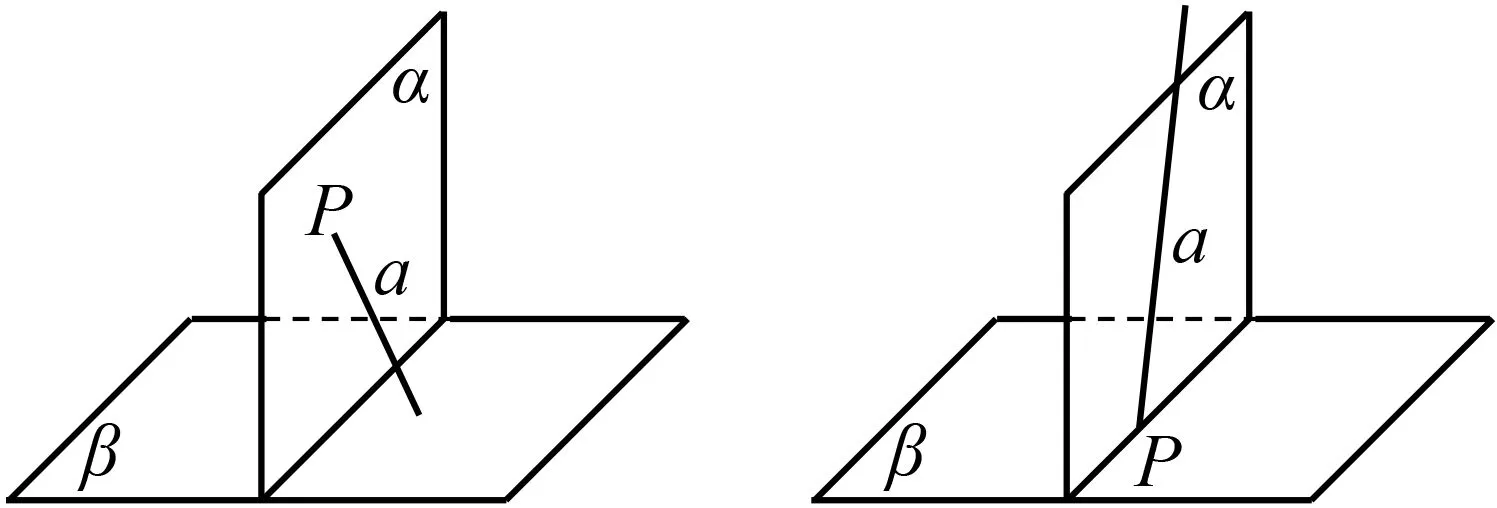
图8 图9

师(追问)：经过一点有几条直线与已知平面垂直？

师：我们知道，过一点有且只有一条直线与已知平面垂直，所以若过一点有两条直线与平面垂直，那么这两条直线重合．

以小组为单位继续讨论，教师巡视之后投影两位学生的书写过程，整理如下：

条件：α⊥β，P∈α，P∈a，a⊥β．

结论：a⊂α．

生1的证明过程如下：

证明：如图10，设α∩β=c，过点P在平面α内作b⊥c．

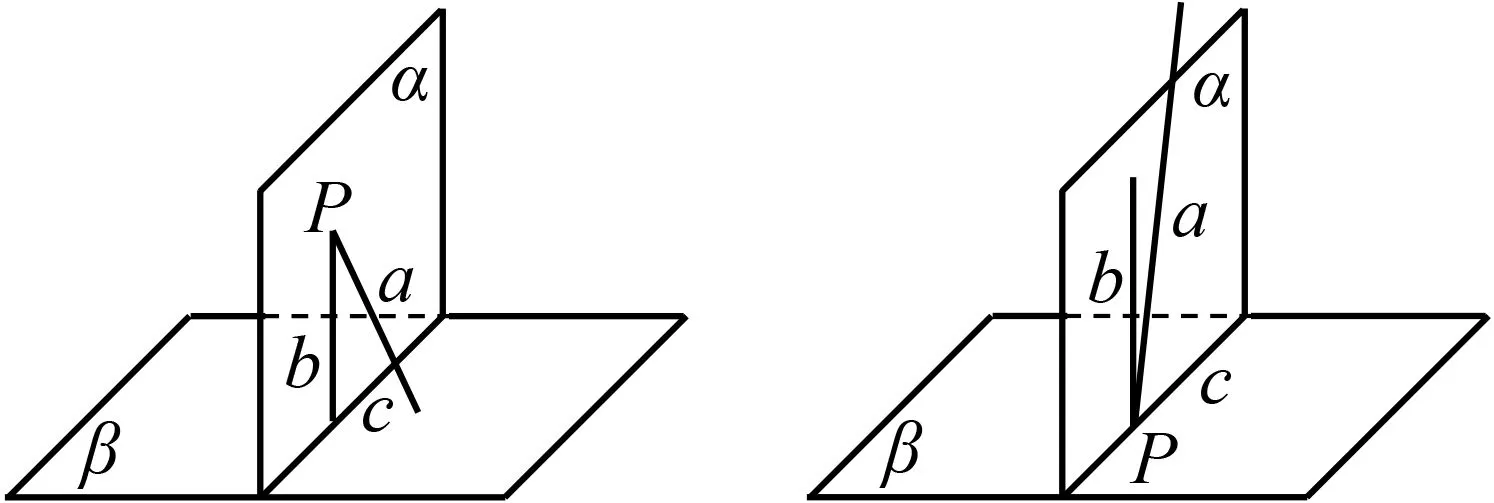
图10 图11

因为α⊥β，α∩β=c，b⊂α，b⊥c，所以b⊥β.

又因为a⊥β，而过一点有且只有一条直线与平面β垂直，所以a与b重合．

生2的证明过程如下：

证明：如图11，假设a⊄α，则a与α相交．设α∩β=c，过点P作b⊥c．

因为α⊥β，所以b⊥β.

又因为a⊥β，所以a∥b．

这与a∩b=P矛盾，即假设不成立，所以a⊂α．

师：请仔细观察两位同学的证明过程，并思考其证明的方法以及使用定理的条件是否完备．

生：在方法2中，使用面面垂直的性质定理时，需满足四个条件，该同学漏掉了b⊂α．

师：很好！也就是我们证明命题时要规范书写．

设计意图对比展示两位学生的证明过程，生1用的同一法，生2用的反证法，在展示与纠错的过程中暴露学生的思维，在规范书写的同时使其体会、反思和总结条件的完备性．

板书(略)．

小组3成果展示：

生：刚才我们研究的都是从背景面中射出的灯光．事实上，舞台的上方也有从不同的角度射出的灯光．如果射出的灯光与地面具有特殊位置关系，那么灯光与背景面是否也有特殊的位置关系呢？

师：你能将上述问题抽象为数学问题吗？

生：两个平面垂直，如果直线不在两个平面内，当直线与其中一个平面具有特殊位置关系，即平行或垂直时，能得到哪些结论？

生1：(猜想)如图12，已知平面α⊥平面β，直线a⊥β，a⊄α，则a∥α．

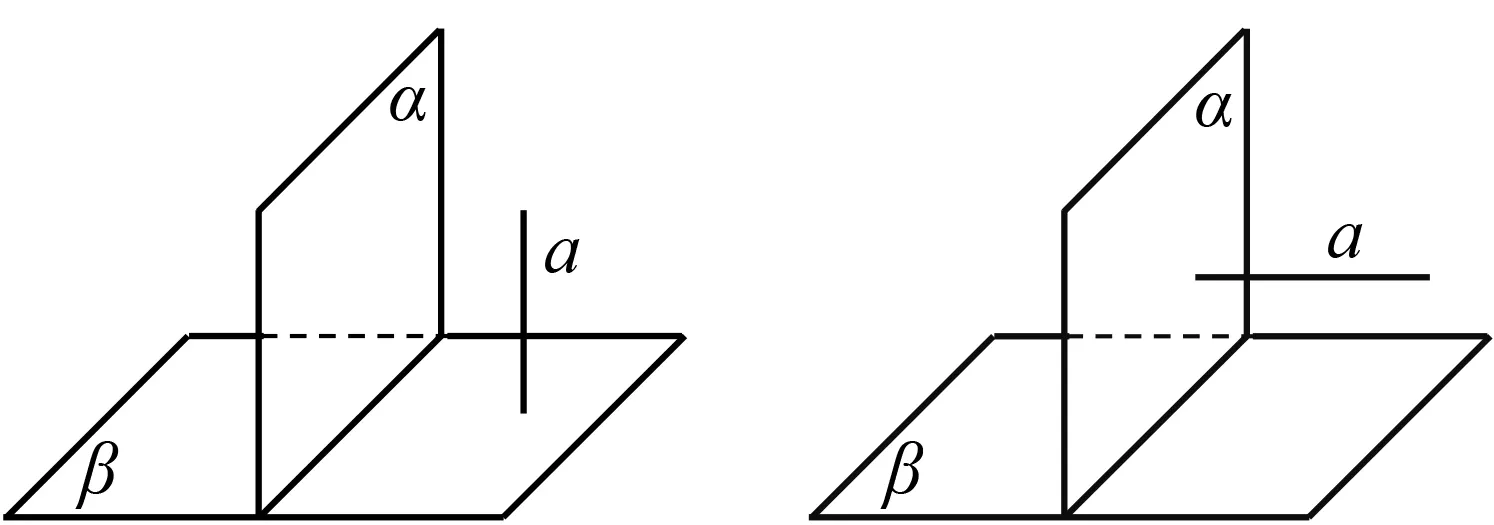
图12 图13

生2：(猜想)如图13，已知平面α⊥平面β，直线a∥β，a⊄α，则a⊥α．

生3：我觉得生2的猜想是错误的，直线a可以旋转，与平面α的关系不确定．

师：说得很好！通过举反例，说明该猜想是错误的，即当直线a∥β时，由于a是可以旋转的，所以并不能确定与平面α的关系．

设计意图探究的过程，不仅仅是发现新性质的过程，也是一个发现错误、找到思维漏洞以及提升思维严谨性的过程．在相互讨论中进行思维的碰撞，在反例教学中培养思维的严谨性．

3.3 演练提升——思考中深化

例题如图14，已知PA⊥平面ABC，平面PAB⊥平面PBC，求证：BC⊥平面PAB．

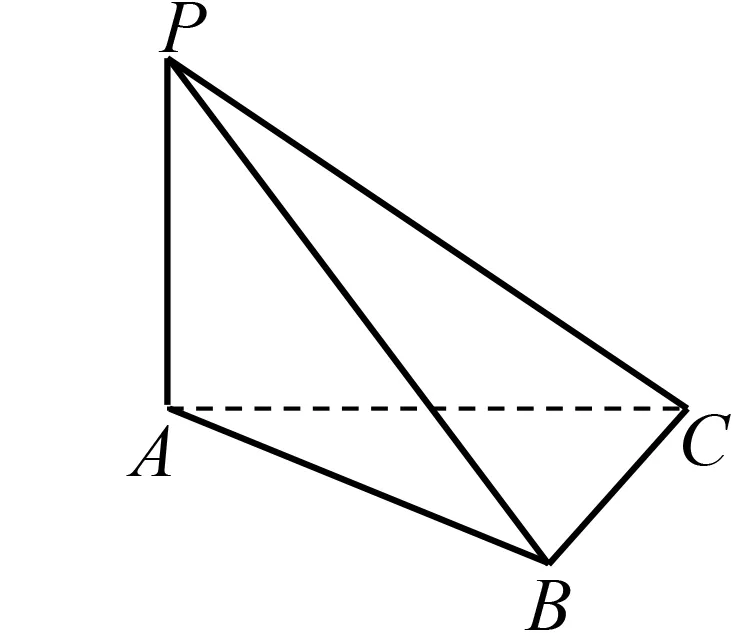
图14

设计意图使用性质定理的关键是在一个平面内找到或作出交线的垂线，同时引导学生体会面面垂直、线面垂直、线线垂直的相互转化，掌握研究直线、平面位置关系的重要方法——转化法．

3.4 课堂小结——回顾中提炼

(1)知识框架

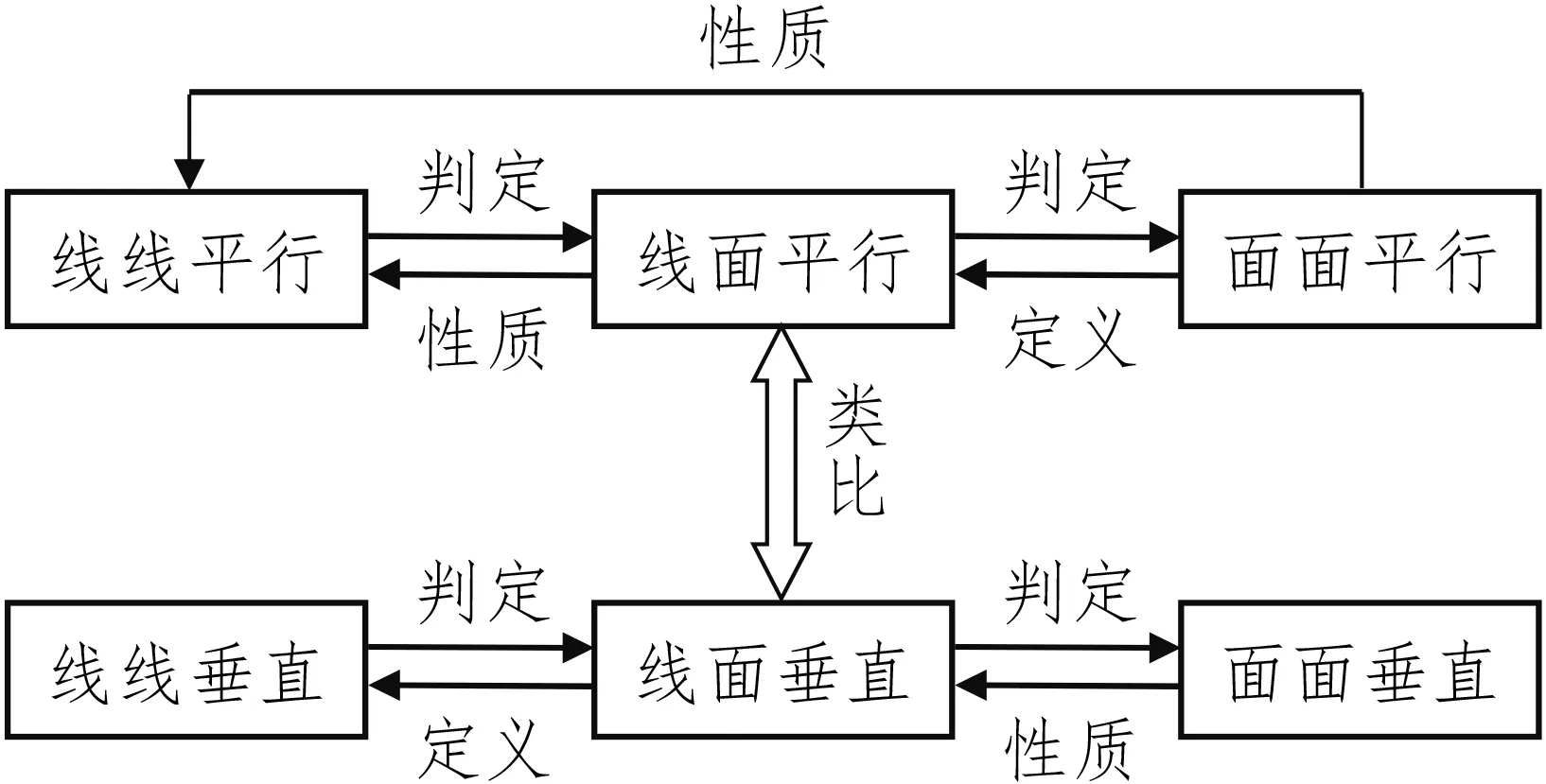
图15

(2)思想方法：分类讨论、类比、转化与化归．

设计意图通过小结，回顾本课所学知识以及本章的知识框架，掌握线线、线面、面面位置关系之间的相互转化，培养学生反思和总结的意识和习惯，体会立体几何研究的内容和方法，同时也帮助学生将所学知识系统化、结构化，掌握学习方法．

3.5 课后拓展——类比中研究

师：类比线面垂直性质定理的探究历程，我们研究了面面垂直的性质定理及结论，请同学们课后思考并探究：两个平面垂直，如果将问题3中的直线换成平面，当第三个平面与已知两平面具有特殊位置关系，即平行或垂直时，又能得到哪些结论？

学生课后探究成果如下：

成果1：如图16，已知平面α，β，γ，且α⊥β，γ∥α，则γ⊥β．

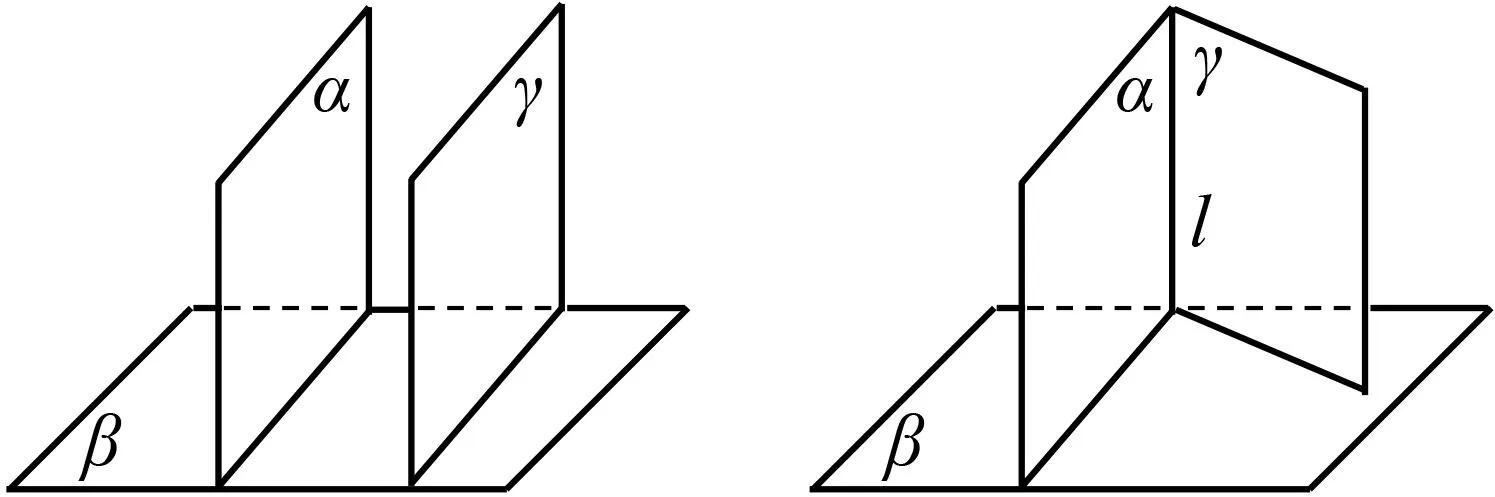
图16 图17

成果2：如图17，已知平面α，β，γ，且α⊥β，γ⊥β，α∩γ=l，则l⊥β．

成果3：已知三个平面两两垂直，则三条交线也两两垂直．

4 教学反思

4.1 注重培养团队协作，提升合作能力

“群体动力”理论认为：在一个合作性的集体中，具有不同智慧水平、不同知识结构、不同思维方式的成员聚集在一起，相互依赖，建立“利益共同体”并成为其中一员，可用集体的力量共同完成学习任务，并形成一个密不可分的整体，相互启发，相互补充，在思维的碰撞中产生新的认识．发现学习注重团队协作、注重探究、注重学生的感知与操作，是主动认识、主动发现的过程，是将学生已有的知识和经验结合起来，类比研究的方法与历程，自主提出问题、解决问题．

4.2 注重训练直觉思维，培养直观想象

直觉思维的结果属于合情推理，所得结果未必正确，但可以充分调动学生的积极性，使其认真思考，经过反复的推理和归纳，去验证猜想的合理性和正确性，在创造性思维的关键阶段起到重要的作用，为逻辑推理提供研究的方向，也为直觉思维转化为逻辑思维提供有力前提．徐利治教授曾指出：“数学的直觉是可以后天培养的，是可以通过训练提高的．”因此，在引导学生进行发现学习时，教师可以根据教学内容的不同，设置合适的情境来培养学生的直觉思维，肯定学生的灵感和猜想，及时给予鼓励，因势利导，解除疑惑，使学生通过自己的直觉获取成功的喜悦．

4.3 注重妙用错误财富，促进动态生成

华罗庚说过：“天下只有哑巴没有说错过话；天下只有白痴没有想错过问题；天下没有数学家没算错过题的．”本节课是在平面与平面垂直条件下研究性质，教师预设了发现学习中可能出现的错误，并思考相应的策略，巧妙利用错误财富，合理地进行引导，让学生经过质疑、思考的认知冲突，促进课堂的动态生成．整个教学过程是开放的，需要不断调整，生成目标．在本节课的成果展示中，小组2第2位学生的证明过程不严谨，小组3第2位学生的猜想错误，这都与教师的预设不谋而合．