捕捉几何错误 洞见数学之美*

刘 鹏 (浙江省义乌市北苑中学 322015)

童桂恒 (浙江省金华第四中学 321001)

杨光伟 (浙江师范大学教师教育学院 310005)

1 问题提出

近些年，数学美作为数学教育领域研究的核心议题之一，其理论之维与实践路径不断发展的同时，也衍生出一系列问题．初中阶段的几何领域中，许多一线教师对数学美的理解存在一些误区，普遍认为数学美就是指一些对称、简单的几何图形，而复杂、错误的几何图形便不具有数学美的特征．事实上，这样的理解是片面的，并没有正确认识数学美的本质．其原因主要有两点：一是对理论的理解存在一些缺陷；二是对具有数学美的几何素材研究得较少，从而在一定程度上阻碍了数学美在课堂教学中的发展．

实际上，具有“几何错误”的图形中也蕴含了数学美，只不过由于课内的素材所呈现的多以正确、易于判断的几何图形为主，很难有新的突破点．这就需要教师对数学美的相关素材进行广泛的涉猎，以填补课内的空白．基于此，结合对数学美的理解与自身阅读经历，与各位读者分享在阅读过程中对于素材的发现，以及如何寻找包含几何错误的图形与数学美之间的联系，从而为数学美融入几何教学提供进路与方略．

2 几何错误与数学美

这里所探讨的几何错误，是指视觉上所看到的几何错误，不是由于不细心或缺乏理解而产生的错误．几何图形常常具有欺骗性，对于呈现在我们眼前的图形，我们往往会受到视觉上的干扰，认为得到的结论一定是正确的，导致视觉受到欺骗从而发生错误的判断．例如，图1中的两条线段，看上去第一条更长一些，实际上两条线段的长度是相等的．这样的几何错误是由于忽视了几何图形确定几何性质和证明几何关系的重要性，以至于对数学美也产生了一定的误解．不仅是在线段问题上，甚至是在对称图形中也会出现这样的情况．

图1

几何学的学习作为发展美学教育的重要途径之一，不仅能够培养学生的几何直观素养，也能够发展学生发现美、欣赏美的能力．张奠宙先生曾指出，数学教学中的美学教育有四个层次：美观、美好、美妙、完美[1]．即“美观”强调数学对象形式上的对称、和谐、简洁等，给人以美感；“美好”强调数学对象的正确性；“美妙”注重学习数学的感受；“完美”则是追求统一、完美无缺．

从几何来看，可以进一步理解为：“美观”指图形的外表美观；并且这种美观需要严格的逻辑证明，这就是“美好”的体现；在几何证明中展示多种数学思想方法，体会方法的乐趣，又称之为“美妙”；最后，回过头来思考，对于具有数学美的几何图形的产生过程，是否可以更为简约、自然或是作进一步的推广？这样的探究才能称得上是“完美”．基于此，笔者根据自己对数学美中“四美”的理解，结合一个具体的几何图形实例加以分析．

3 案例分析

3.1 生活与数学的“美观”共情

笔者在阅读过程中，发现了一类关于正八边形的图形以及作图方法[2]，将其整理如表1．

表1 正八边形的作图方法

初看这5个图形，均给人一种视觉上的美感．每一个图形中均包含了圆、等腰三角形、等腰直角三角形、正方形等不同的几何图形．这些数学对象均能够给人一种形式上的和谐、优美的感觉．据记载，作法1由艺术家兼几何学家奥古斯丁·希尔施富格尔于1543年首次发现，是艺术与数学相结合的产物；作法3是金匠海因里希·兰登萨克于1564年首次发现，是手工艺与数学相结合的产物；作法5是由阿基米德作出的，我们都知道他是数学家、哲学家、物理学家，可以说是多个知识领域的智慧结晶，自然不意外．美观作为数学美的第一层次，从形式上看，体现在数学图形使人看起来舒服．从来源上看，数学美源于生活中艺术、手工艺、多个学科领域等，将它们与数学相融合．由直观的美学印象从生活中的事物迁移到数学中，以几何图形的性质与结构呈现数学美，这正是一个数学美与生活中的美相辅相成的过程．

3.2 “美好”与“美妙”共舞

针对上述图形，笔者第一反应是猜测如此对称美观的几何图形，应该都是正八边形吧．展开证明，却发现了一些几何错误！结合五种作法，给出相应的具体解析或证明：

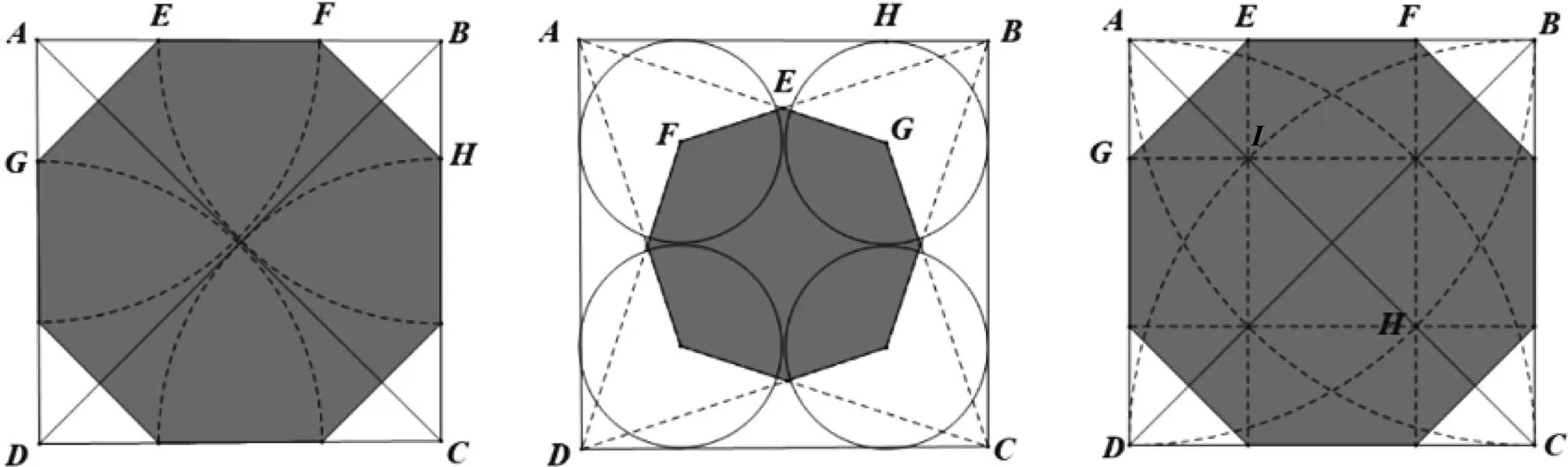
图2 图3 图4

如此优美的几何图形，竟然不是正八边形！

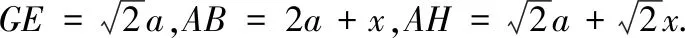
解析4如图5，因为△AEG和△BEH是全等的等腰直角三角形，得GE=EH．且直线GF和EF均为角平分线，得∠FGE=∠FEG=22.5°，∠GFE=135°，得△FGE为等腰三角形，GF=FE．同理，得△IEH为等腰三角形，EI=IH，∠IEH=∠IHE=22.5°．可由角边角关系推出△GFE和△HIE全等，得到邻边EF=EI.同理可得阴影部分图形的所有邻边相等．同时，也可以得到∠FEI=135°，从而推得所有的内角都相等．因此，作法4正确．

图5 图6

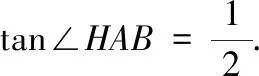
四美的呈现是一个渐进的过程，“美观”的几何图形必须上升到“美好”的层次．作为数学美的第二个层次，从几何图形的性质与结构出发，只有认识到几何图形的正确性，才能体现“美好”．正八边形既是一个轴对称图形，更是一个中心对称图形．多数学生会以为通过观察、操作所得到的几何图形具有对称美、和谐美的特征，就一定是正八边形．本例凸显了观察与经验理解的局限性以及逻辑推理的重要性．笔者根据正八边形的定义，对五个作法展开了简单的解析，将直观经验转化为演绎推理，发现了作法2与作法5所得到的八边形并非是正八边形，与视觉上所看到的截然不同．两种作法得到的均是等边不等角的八边形，可见“美观”的外表需要“美好”的几何证明来验证，而不是凭借简单的视觉，那样往往会产生错误．

“美妙”作为数学美的第三个层次，体现在“美好”的几何图形探究过程中，所运用的数学思想方法上．首先，以上五个证明均渗透了数形结合的思想，将几何证明代数化．通过这样的例子，能够进一步感受代数中的证明和几何中的观察、操作之间的联系，实现从实验几何到代数几何的跨越．其次，我们看解析1与解析4，均从图形的基本性质和属性出发，解析1采用假设法这一数学方法，将边长具体化，利用等腰三角形的特殊性，得到八边形边长的数量关系和位置关系，解析4直接由多个等腰三角形与角平分线的性质得到八边形的内角关系，由角的关系再推得边之间的关系，层层递进；再次，作法2与作法5的证明，在假设法的基础上结合反证法与三角函数的运用，通过假设边长计算得到内角的三角函数值，与tan 22.5°进行大小比较来证明结论，使得思维含量进一步增大．对学生来说，不仅能够想到三角函数来证明几何，还能求特殊角一半的三角函数值，这是多种数学方法与知识的交汇，更是方法的美妙结合；最后，解析3中引入了方程思想，设未知数，根据正方形的边长与圆的半径之间的等量关系建立方程，得出八边形边长的关系．由此可见，一个看似简单的几何图形背后，却能够隐藏着如此多的数学思想方法，怎么能不让人感到美妙？可以想象，当学生经历发现、解决问题的过程后，是否也会和笔者一样体会到数学的妙不可言，对数学产生由衷的兴趣呢？

3.3 几何与“完美”共生

从数学发展来看，数学美经历了美观—美好—美妙的三个层次，并没有止步于此，而是做到至善至美，追求极致，便产生了“完美”．正如怀特海先生所说：“数学的魅力在于来自一般原理的互相影响的大量推论，它们之间的复杂关系，与争论的出发点之间的明显的疏远，形式多样的方法，抽象的特征所带来的不朽真理．”[3]正是这种魅力引发笔者猜想，如果没有圆规能否得到正八边形呢?探索后找到一种折叠的方法：

如图7所示，由一张长方形纸片，将其对折两次，再按照45°角进行折叠，折出45°角的折线之后，通过直尺取折线上到图形中心等距离的点，得到正八边形．可以看出，得到正八边形的方法在几何中绝不仅仅只有作图法，还有折叠法等．总体看，从古至今，不论是欧氏几何公理体系的建立还是解析几何与微积分的创立，或是勾股定理证明的无尽探索等，无论是对一个方程解的探究还是对动点问题的分类讨论，都是追求“完美”的表现，或许这才是数学美的最高境界吧！

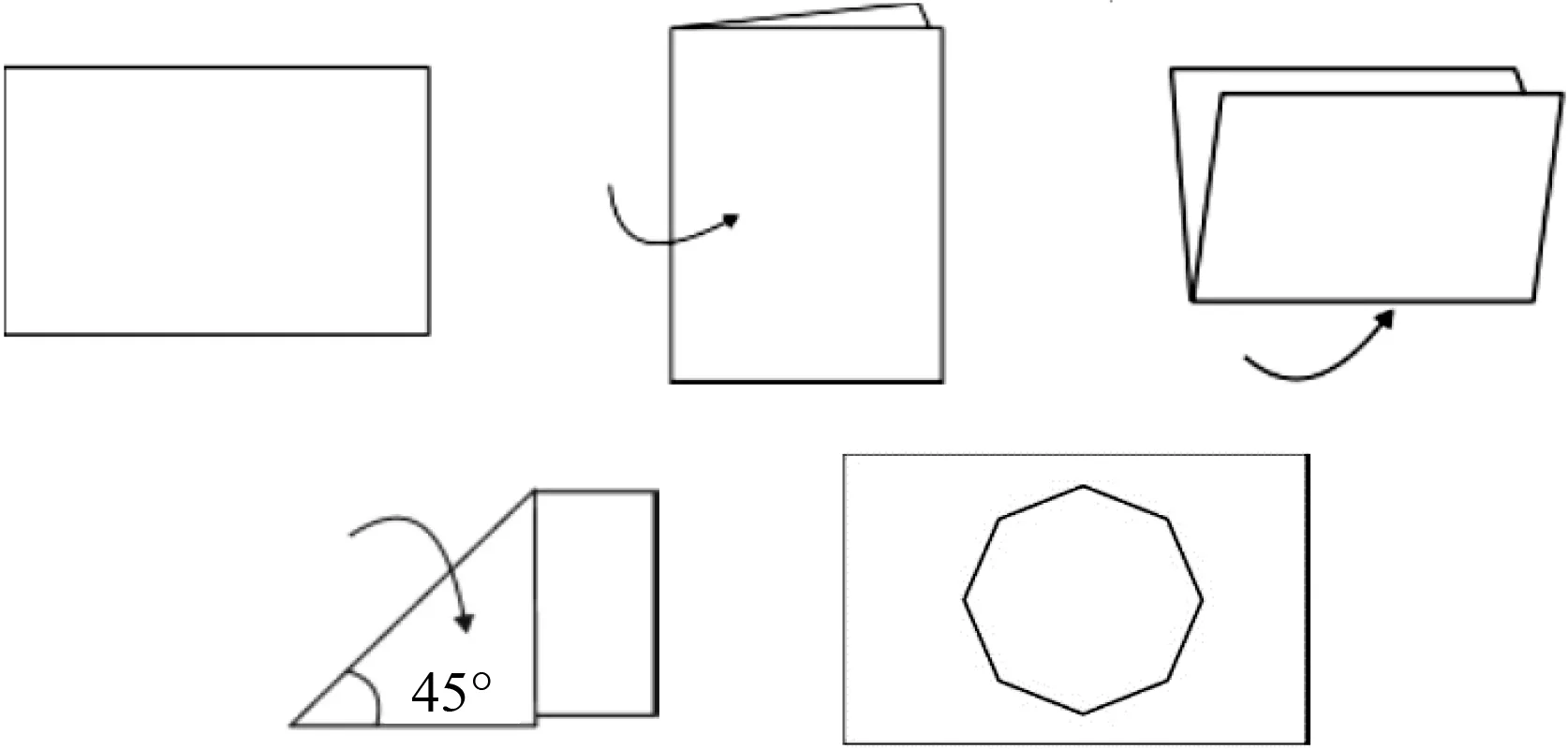
图7

4 四美渐进

在正八边形作图的相关问题探究中，先是从几何图形“美观”的外表，联系生活实际，深入到逻辑证明的“美好”，再从几何图形的证明过程中分析归纳出各种方法的“美妙”，最后，扩展联想出得到正八边形的其他途径，不能说得上是“完美”，却是以追求“完美”为最终目标．实际上是一个“四美渐进”的过程，张奠宙先生所提出美观、美好、美妙、完美四个层次，并非是孤立的，毫无关联的，而是相互联系与作用的．尤其是在几何领域中，本文对数学美的解读又有了新的含义．简而言之，我们只有在生活中关注点滴细节，或是在课内与课外挖掘蕴含数学美的各种素材，见微知著，勤于反思，才能领悟数学美的真谛．那么，当我们发现了这些素材，如何能够在教学或探究中使用这些素材，如何能够将数学美真正地融入课堂教学，这些又需要教师们进一步思考与实践．