指向高阶思维的数学课堂教学实践与思考*

谢俊峰 (江苏省扬州市朱自清中学 225009)

1 问题的提出

高阶思维是指发生在较高认知水平层次上的心智活动或认知能力，它在教学目标分类中表现为较高认知水平层次的能力，如分析、评价、创造[1].2016年我国发布了《中国学生发展核心素养》.核心素养以培养“全面发展的人”为核心，分为文化基础、自主发展、社会参与三个方面，综合表现为六大素养，其中科学精神中的理性思维、批判质疑、勇于探究，学会学习中的勤于反思，实践创新中的问题解决等基本要点都指向学生高阶思维的发展.这些素养的培养与发展，都基于学生高阶思维的培养，学生的高阶思维能力强了，则学生的核心素养也会得到相应的发展.因此，随着核心素养研究的深入，教育界对高阶思维的研究热度也在逐渐升温.

数学是思维的体操，是展现思考最纯粹形式的科学，是培养和发展学生高阶思维的重要学科.核心素养、高阶思维的培养必须以数学知识内容为载体，在教学中我们要深刻理解教学内容，挖掘其中蕴含的高阶思维培育素材.下面结合苏科版教材九年级上“解一元二次方程(配方法2)”这一节课来谈谈如何理解教学内容，挖掘高阶思维孕育点，培养学生的高阶思维.

2 指向高阶思维的教学实践

2.1 教材设计及思考

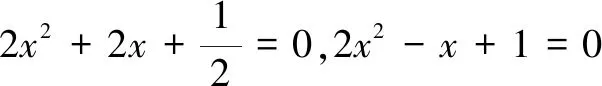
这节课笔者听过两次，课堂上教师出示例题4，反应快的学生说：将二次项系数化为1，然后进行配方，从而求解.教师肯定了学生的回答，强调了“转化”的数学思想方法.例题5的讲解也是同样的思路.两道例题后就是进行相应的巩固、变式练习.课后笔者追问了上课教师两个问题：一是不把系数化为1，能不能用配方法求解?二是是不是系数化为1对用配方法求解所有的一元二次方程都方便或简单？教师听完问题，陷入了思考.

在笔者执教这节课的时候进行了如下的教学设计，对学生思维、特别是高阶思维的发展十分有益，现整理出来与大家分享.

2.2 指向高阶思维的教学设计

问题1昨天我们学习了配方法解一元二次方程，大家回忆一下配方法解方程的步骤及易错点.

设计意图通过复习，进一步巩固配方法解一元二次方程的步骤，为本节课的学习打下基础.

问题2尝试解方程2x2-5x+2=0，你是怎么想到这样解的？

教学场景 部分学生将系数化为1后配方求解.学生分析思路的由来：这个方程与上节课所学的方程不同(二次项系数不为1了)，将不会解的方程转化为已经会解的方程.其中有一部分学生在直接进行配方时出现了错误.

设计意图在解方程前没有引导学生去将二次项系数化为1，而是学生自己尝试去解题，并让学生汇报交流是怎么想到这样解的，反思分析思路的由来.部分学生直接配一次项系数一半的平方，得到了错误的解法.让学生在解题中暴露出问题，再进行纠错巩固.这样的过程是学生自主探究学习的过程，即使出现错误也是有价值的，因为学生会分析错误的原因，加深对知识的理解.

问题3基于对完全平方式的认识，方程2x2-5x+2=0系数不化为1可不可以求解？先思考，再交流.这样的配方对大家有什么启示？

设计意图本题中学生直接配方来求解方程，过程比较复杂，最后不一定能求出答案，但这样的过程可以让学生对完全平方公式有更全面的理解，对教材上“把系数化为1”这句话的含义有了更深的理解，也让学生对各种解法有自己的评价和判断，一般情况下系数化为1后再配方可以简化运算.

问题4对于“将系数化为1”这句话，你还有什么思考？(如果学生没有思考结果，可以进一步明确问题：系数化为1一定就简单吗？你能不能写出一个方程直接配方更简单呢？)

教学场景 学生先单独思考，然后小组讨论，最后再全班交流.有些组得出结论“有一些方程直接配方会比较简单，系数化为1反而复杂了”，并举出了例子，方程9x2+6x-4=0⟹9x2+6x=4⟹ (3x)2+2·3x·1+12=4+1⟹(3x+1)2=5，……

教师让学生再设计一些类似的方程.

设计意图这个问题设计是让学生进一步思考(不是所有的一元二次方程将二次项系数化为1都会简化运算)，突破“二次项系数化为1”的思维定势和束缚，要根据具体问题进行具体分析，这对学生思维能力的要求较高.在问题的提出上，不是教师直接给出方程让学生求解，而是让学生进行思考，自己设计方程、自己求解，比求解方程的要求更高，思维的层次也更高，更有利于培养学生的创新思维.

问题5通过刚才问题的解答，思考方程2x2-5x+2=0有没有其他的解法？你是怎么想到的？

教学场景 有学生提出了自己的解法，并进行了分析：对比上面的问题，我们可以在方程两边同时乘以2，将方程二次项系数转化为平方数，然后配方求解.

教师追问：这种解法与系数化为1后配方求解，以及直接配方求解相比，大家觉得哪一种方法相对简单？

设计意图学生通过分析该方程与问题5中大家设计的方程比较，提出了一种新的解此类方程的思路，并在教师的引导下评价此类方程的三种不同解法，从而从中选择最佳的方法.在此过程中，学生的分析、评价、创造等高阶思维都得到了发展.

问题6通过今天的学习，对于二次项系数不为1的一元二次方程，请你总结一下它的解题步骤是什么？涉及的数学思想方法有哪些？

设计意图通过回顾本节课的学习，让学生总结归纳二次项系数不为1的一元二次方程的解题步骤，让学生注意解题前先观察方程再选择合适的方法解题，培养学生的审题习惯.同时让学生总结本节课渗透的数学思想方法，进一步发展概括、归纳等高阶思维，如分类讨论、转化与化归等.

问题7本节课中老师提出了哪些关键问题？这些问题是从哪些角度提出的？

教学场景 学生在教师带领下，回顾了本节课所提出的问题，教师形成了下面的板书(图1).

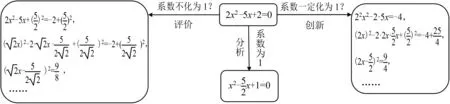
图1

设计意图在课堂小结环节，我们往往从数学知识及数学思想方法的角度进行总结，但对于教师问题的设计方式、为什么设计这样的问题、怎样设计问题，往往不够重视.通过追问“问题的问题”，让学生在分析、解决问题的基础上，学会发现问题、提出问题，在学习知识的基础上，知晓知识的来龙去脉.

3 指向高阶思维教学实践的思考

3.1 研究教材内容，挖掘高阶思维发展素材

因为编写的需要，教材中的教学内容一般以知识的“学术形态”呈现，教师在教学中需要将知识的“学术形态”转化为“教育形态”，促进学生火热的思考，因为只有火热的思考才有可能促进学生高阶思维的发生.李庾南老师提出的学材再建构、学法三结合、学程重生成的“三学”课堂，学材再建构就是教师在备课、选取教学内容时要重视研究教材，要基于理解数学、理解教材、理解学情的前提，进行教学内容的重组、设计[2].

教师在学材再建构过程中要注重挖掘有利于学生思维、特别是高阶思维发展的素材，依托这样的素材进行教学设计，在潜移默化中培养学生的高阶思维.本节课中，如果按照教材内容来教学，很快就能完成新知讲解，然后是大量机械、程序化的模仿运算.长期如此，学生只会停留在识记、理解、简单运用的认知层面，其高阶思维不能得到发展.因此，教师不可简单地说一句“转化”就完成教学任务，而是要分析新方程与已学方程的不同，让学生自己产生“转化”的思路；要深刻理解完全平方公式，可以不将二次项系数化为1，自我评价解法的优劣；突破固有思路束缚，引导学生创新性地思考怎样的方程可以不用将二次项系数化为1.这样这节课的例题教学才会深刻，学生的高阶思维才能得到发展.

3.2 注重问题设计，促进高阶思维深度发展

问题是思维的起点，是数学的心脏.问题是学生探究学习的驱动器和导航仪[3].数学课堂教学设计的关键是问题的设计.教师在备课时，要根据教学内容以及学生心理特点，设计课堂教学的核心问题，并围绕着核心问题设计一连串的小问题，以问题来驱动课堂教学进程，引导学生进行自主探究与合作学习，激发学生的学习兴趣.

本节课中设计的两个核心问题：一是系数不为1的一元二次方程能不能用配方法求解.学生在前面的学习中总结了将系数化为1这一解题策略，但为什么一定要这么做？不这么做行不行？该问题引导学生进行分析，得出了直接配方的方法，并在直接配方后能评价两种方法的优劣.二是对于“系数化为1”你还有什么思考.这是一个结构不良问题，具有开放性，学生可以大胆设想，积极思考.经过小组合作与讨论，创新得出第三种解法，并再次评价这种方法与前面两种方法的优劣.好的问题不仅能串联起课堂教学，更为重要的是在问题驱动下，学生分析、评价、创造等高阶思维的能力得到了发展.

3.3 突出学生主体，驱动高阶思维自然生成

以学生为中心的课堂是影响高阶思维技能发展的一个关键因素.学生是学习的主体，也是思维的主体，教师的问题设计得再好，学生没有参与或者没有积极思考，那么学生的思维也不会得到发展.突出学生的主体，就需要让学生参与课堂活动.在课堂教学中，我们要努力建立以学生为中心的课堂，这种课堂支持学生公开表达观点，强调学生自己主动经常性参与思维实践，能够提供有效的思维建模过程，发展思维技能，并激发学生的学习[4].

本节课的教学设计中，教师在提出问题2～问题7之后，都没有急于给出答案，而是给予学生充分的独立思考时间，然后采用小组合作，学生在交流碰撞中产生思维的火花，最后再进行班级的交流.在这样的过程中，学生的思路会越来越清晰，高阶思维能力也在潜移默化中得到生长.

3.4 关注课堂小结，强化高阶思维生长过程

课堂小结环节是教学设计的薄弱环节.在常态课中教师常常因为时间原因而不能进行课堂小结，甚至认为这个环节可有可无.在一些公开课、研究课上，课堂小结环节往往就是提出一些常见的问题：本节课你学到了什么？稍好一点的课堂小结会在总结本节课知识的同时，追问本节课的思想方法有哪些.这些课堂小结关注的是学生知识的收获，但对学生高阶思维的培养而言则较少涉及.而学生发现并且学会发现、提出问题的能力更加重要，这就是高阶思维方面的认知.

在本节课的总结环节，教师梳理本节课的教学流程，通过添加一些箭头、方框，突出了核心问题，形成了“结构化板书”，学生对本节课的思维过程和思考的方向有了更深入的理解.更为重要的是让学生形成高阶思维的习惯.通过这样的总结，就是要培养学生能够学会，并经常性地提出像本节课中“系数不化为1？”“系数一定要化为1？”等等这样反思性的问题，形成良好的思维习惯，这样学生就可以达到一题多解、多解归一，甚至是多题归一的层次.学生的思维能力就会不断得到发展与提升，学生的思维也会由低阶思维走向高阶思维.