屏障环境中大小鼠养殖搬运机器人运动参数优化

夏绪辉，端木艳霞，刘 翔，王 蕾，张泽琳

(武汉科技大学冶金装备及其控制教育部重点实验室，湖北 武汉，430081)

现代生物医学科研所用的大小鼠必须饲养在安适、无应激和受控的屏障环境中，以最大限度地减少外界干扰因素对其产生影响。在屏障环境自动化养殖系统中，搬运机器人按照预先设定的运动参数和程序完成取笼、搬运、换笼、放回等一系列更换鼠笼的动作。如果运动参数设定太大，鼠笼在搬运过程中不仅容易产生振动，使笼中的大小鼠受到惊扰，而且还会增加搬运能耗和养殖成本；相反地，如果运动参数设定太小，更换鼠笼的效率会降低，不利于开展大规模养殖活动。因此，搬运机器人运动参数的优化是屏障环境中大小鼠自动化养殖的一个核心技术问题。

目前鲜有专门针对实验动物饲养场所搬运机器人的运动参数优化研究，但其他应用领域的机器人运动参数优化研究成果可作为借鉴。相关研究主要集中在以下两个方面：

(1)面向运行时间最优的单目标运动参数优化。例如，钱虹等[1]建立了机器人螺旋轨迹运行参数的优化控制模型，采用BBO算法进行求解，使机器人在最优参数下的运行时间最短。李小为等[2]研究了速度约束下的机械臂运动时间优化问题，利用PSO算法在多项式插值时间变量空间进行搜索，得到六自由度机械臂在约束条件下的最短运行时间。王琨等[3]建立了机器人关节空间位置、速度、加速度相对于归一化时间的数学模型，在保证机器人轨迹平滑的基础上使机器人运行时间最优。曹波等[4]提出一种基于时间最优的码垛机器人运动路径规划方法，采用三次样条曲线拟合搬运机器人的运动轨迹，使参数优化后的码垛机器人工作效率明显提高。Guo等[5]选用B样条插值函数拟合机械臂运动轨迹，采用PSO算法对机械臂的运动时间进行优化。Zhang等[6]使用三次Hermite插值多项式对机器人加工路径进行参数化建模，然后对这些参数进行优化，从而在最短时间内完成加工任务。上述方法主要采用高次多项式或样条曲线对机器人运动轨迹建模，然后利用优化算法对模型寻优，但限于模型的表达能力，机器人最优运行时间可能不在优化算法的解空间中，因此其结果不一定是全局最优解。此外，上述方法以机器人正常运动为前提，未考虑振动对负载造成的不利影响，即使得到全局最优解，也不能保证该结果对负载的影响是最低的。

(2)面向时间与能耗最优的多目标运动参数优化。蒲玉学等[7]以工业机器人运行时间最优、能耗最优为目标，采用引入贪婪选择策略的引力搜索算法进行多目标轨迹优化。施祥玲等[8]通过五次NURBS曲线模型构建高阶连续关节运动轨迹，并用多目标粒子群优化算法以运行时间、能量消耗和轨迹脉动为目标进行优化，获得Pareto最优解集。Taitler等[9]研究了机械系统在完工时间和能量组合条件下的最优轨迹规划问题，并利用庞特里亚金极大值原理求最优解集。夏绪辉等[10]建立以绿色度最大化为目标的立体仓库机器人路径规划模型，采用免疫蚁群算法求解，结果表明该方法能有效平衡搬运机器人的能耗与作业效率。上述研究考虑了能耗因素对路径规划的影响，在能耗与效率之间寻求最佳平衡点。然而，在目标函数中考虑能耗影响往往会引起机器人运动加速度曲线不平滑，给机器人带来振动与冲击[11]。显然，当机器人负载对运动平稳性要求较高时，上述方法均存在不足。

从现有文献来看，相关研究主要聚焦于优化机器人的运动时间与能耗，对机器人运动平稳性的考量也仅限于其运动轨迹是否足够平滑，而很少考虑运动平稳性对负载感受舒适度的影响。为此，本文根据屏障环境中自动化养殖大小鼠的特殊要求，考虑换笼过程中搬运机器人运动参数对大小鼠产生的刺激影响，同时兼顾大规模养殖对搬运时间和能耗的要求，建立以大小鼠在搬运过程中应激程度最低、搬运时间最短以及能量消耗最小为目标的多目标优化模型，采用基于正态分布交叉的NSGA-II算法求取模型的Pareto解集，并通过案例仿真验证所建模型的正确性及算法的有效性，为屏障环境中自动化动物养殖系统的改进提供思路及方法。

1 问题描述与数学建模

1.1 问题描述

图1所示为屏障环境大小鼠自动化养殖仓库。在屏蔽养殖空间内，对温度、湿度、氨浓度、微生物浓度、风速等指标均有严格规定，饲养架安放在屏蔽养殖空间内，每个架格上放置养殖笼具。搬运机器人在养殖空间中将笼具从架格上取下并搬运到换笼工作台所在的位置进行换笼，换笼完成后再将其放回至原来的架格上，其中，干净的笼具通过传送带送入屏蔽空间内，经过交换的已被污染的笼具通过传送带送出屏蔽空间。由于换笼过程依靠换笼工作台及其附属组件完成，设计时已经考虑到将换笼动作对大小鼠的刺激降到最低，因此本文在建模时不考虑该动作的影响，也不将换笼过程的时间与能量消耗计算到数学模型中，仅考虑搬运机器人在取笼及放回笼具两个阶段的运动参数对大小鼠造成的刺激影响、运动时间和能量消耗。

图1 屏障环境大小鼠自动化养殖仓库示意图

根据养殖规模大小和对换笼频次的要求，可将搬运机器人的搬运模式分为两类。第一类是养殖规模较小或换笼频次较低时，搬运机器人每次搬运一个笼具到换笼地点进行笼具交换，然后将其放回原处，再返回到出发点等待下一次搬运指令；第二类是养殖规模较大或换笼频次较高时，搬运机器人将前一个笼具放回饲养架后，不再返回出发点等待下一次指令，而是直接前往下一次搬运的地点准备搬运。后文称第一类搬运模式为单次模式，第二类搬运模式为连续模式。

1.2 条件假设

为了体现本文的研究重点，降低模型的复杂程度，对建模条件作出以下假设：

(1)假设换笼工作台位于屏蔽空间的原点位置(0,0,0)，且搬运机器人的出发点也位于(0,0,0)，饲养架中每个架格的坐标为(x,y,z)，分别对应所在货架的排、列、层。

(2)假设大小鼠的应激反应主要由搬运机器人的加速度变化引起。因为在垂直方向上加速度的变化会引起超重与失重，并且这种应激刺激明显强于水平方向上加速度变化引起的应激刺激，所以为了简便起见，本文假设搬运机器人在水平方向上只做匀速与匀变速运动，在垂直方向上的运动则分为两种情况：第一种是搬运机器人空载时，由于此时搬运机器人的运动并不对大小鼠造成影响，故假设此时搬运机器人做匀速与匀变速运动；第二种情况是搬运机器人有负载时，此时搬运机器人加速度的不同变化情况会对大小鼠造成不同的应激刺激，故假设此时搬运机器人做变加速运动。

(3)假设搬运机器人在变加速运动阶段服从“静止—加加速—匀加速—减加速—匀速—加减速—匀减速—减减速—静止”的变速过程。

1.3 运动时间分析及模型构建

在构建数学模型之前，将后文用到的主要变量符号及其含义列于表1。

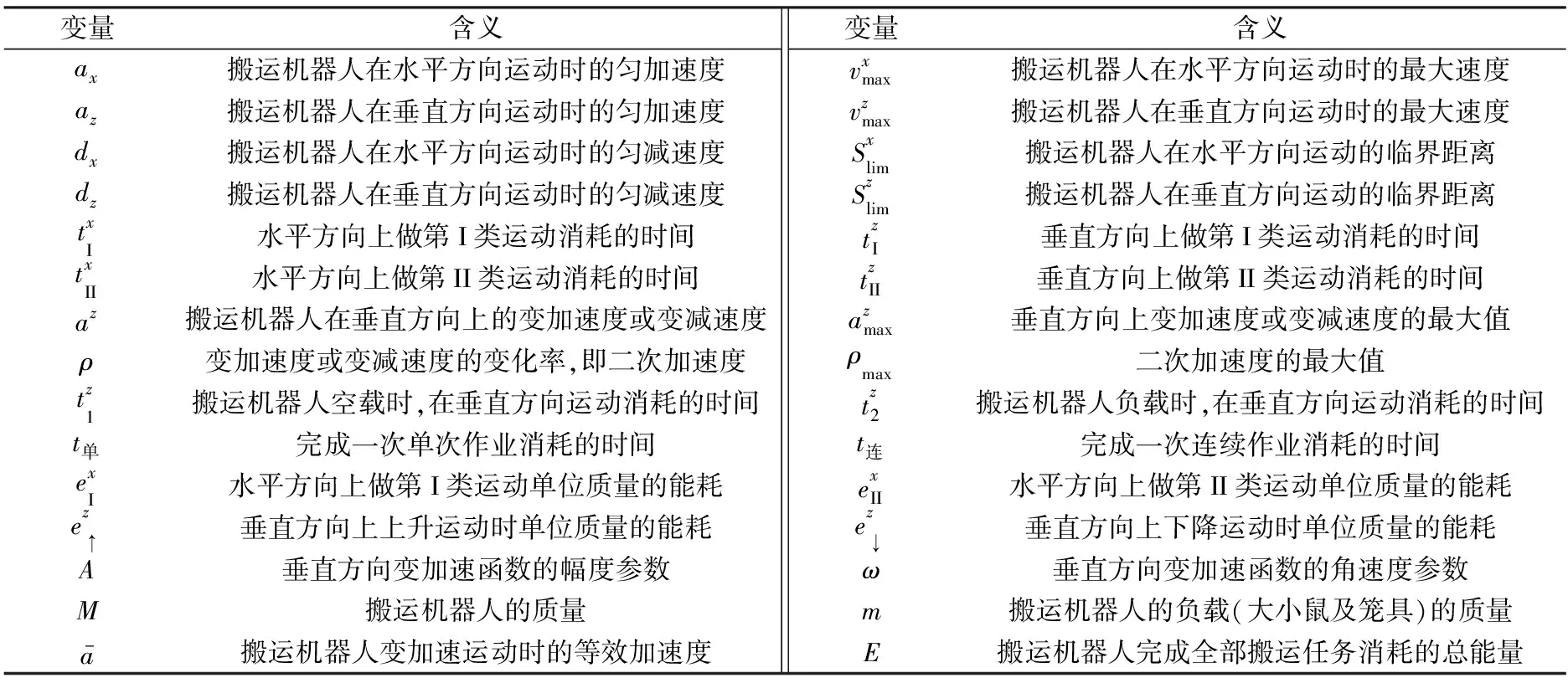
表1 主要变量符号及其含义

1.3.1 搬运机器人在水平方向上的运动分析

搬运机器人在运动过程中存在速度变化，根据其速度能否达到额定值(vmax)，将运动形式分为第I类运动(Stri≤Slim)和第II类运动(Stra>Slim)[10]，如图2所示。

(1)

1.3.2 搬运机器人在垂直方向上的运动分析

(1)搬运机器人空载的情况

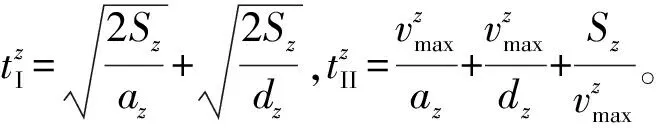
(2)

(2)搬运机器人负载的情况

当搬运机器人负载时，在垂直方向上做变加速运动。目前主要使用抛物线或正弦曲线来描述变加速运动的速度变化曲线，但是在抛物线与直线的过渡段，二次加速度会产生跳变，而采用正弦曲线过渡时则可避免这种跳变现象[12]，因此本文假设变加速或变减速阶段的加速度az符合正弦函数变化规律：

az=Aωsin(ωt)

(3)

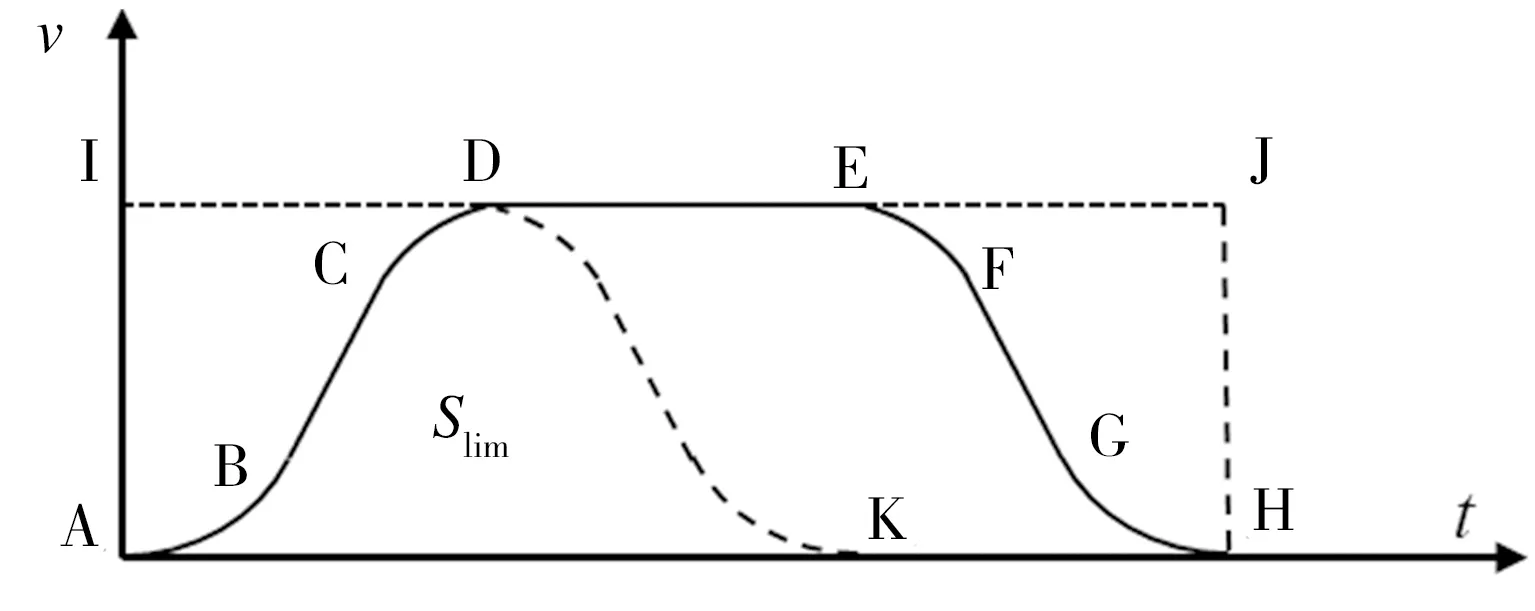
图3 搬运机器人负载时垂直方向的速度变化

ρ=Aω2cos(ωt)

(4)

加速度的最大变化率为：

ρmax=Aω2

(5)

据此，图3中的临界距离满足:

(6)

搬运机器人负载时垂直方向上的运动距离Sz即为曲边梯形ADEH的面积。根据前面的假设条件可知：曲边梯形ADEH的面积=矩形AHJI的面积-曲边三角形ADK的面积。将相关变量代入上述关系式，整理可得式(7)：

(7)

需要指出，建模时默认实际运动距离大于临界距离且假设变加速(减速)各段曲线满足对称性的原因是：利用定积分的几何意义将繁琐的定积分计算转化成对曲边梯形的面积计算，以此降低计算量，同时简化建模过程，使数学模型表达式更加简洁。

1.3.3 搬运机器人运动总时间

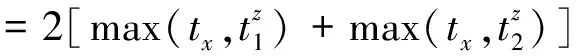
(8)

同理，当搬运机器人完成一次连续作业时，除了考虑机器人取笼与放回的时间，还要考虑机器人在仓库中空载从前一个目标仓位移动到后一个目标仓位消耗的时间，如式(9)所示：

(9)

设在一次完整的作业任务中，搬运机器人需要完成Q1次单次作业和Q2次连续作业。那么在这次任务中搬运机器人在水平和垂直方向上运动的总时间为：

(10)

1.4 运动能耗分析及模型构建

搬运机器人在一次完整的搬运任务中的能耗包括其在水平方向上的能耗、垂直方向上的能耗以及摩擦造成的能耗，为了便于建模，本文忽略各零件间摩擦造成的能耗。

(11)

(12)

设mi为第i次单次作业负载质量，mj为第j次连续作业负载质量，则搬运机器人完成Q1次单次作业和Q2次连续作业的总能耗为：

(13)

1.5 目标函数

考虑到在搬运中大小鼠对舒适度的要求以及养殖企业对搬运效率与能耗的要求，目标函数主要对影响搬运中大小鼠舒适度的二次加速度和影响搬运作业效率与能耗的搬运时间与搬运总能耗3个指标进行优化。

(1)搬运二次加速度

根据电梯行业设计经验，电梯运行时的加速度和加速度变化率应该限制在一定范围内，一般而言，加速度的最大变化率不应超过1.5 m/s3，否则会导致人体不适[13]。以此类推，大小鼠在搬运过程中所受刺激与速度关系不大，但与二次加速度正相关，即二次加速度越大，大小鼠受到的刺激越强，因此在目标函数中将二次加速度的优化目标定义为：minρ(A，ω)。

(2)搬运时间

搬运时间指搬运机器人完成Q1次单次搬运与Q2次连续搬运作业消耗的总时间，由式(10)给出。为了提高搬运作业效率，目标函数中将搬运时间的优化目标定义为：minT(A，ω)。

(3)搬运能量消耗

搬运能量消耗指机器人完成Q1次单次搬运与Q2次连续搬运作业消耗的总能量，该表达式由式(13)给出。目标函数中将搬运能量消耗的优化目标定义为：minE(A，ω)。

根据上述分析，可将本文多目标优化的目标函数定义为式(14)，其中，优化目标ρ、T与E均是决策变量A与ω的函数。约束条件如式(15)～式(20)所示。通过多目标优化算法确定一组或几组同时使3个目标函数均达到或近似最优的A与ω的组合，并计算出相应的3个优化目标函数值。

(14)

s.t.：

l≤Sx≤L

(15)

h≤Sz≤H

(16)

(17)

(18)

mmin≤m≤mmax

(19)

ρmin≤ρ≤ρmax

(20)

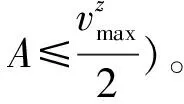
2 基于正态分布交叉的NSGA-II算法

通过观察式(14)可以发现，该问题中的3个目标函数之间存在矛盾。若增大A与ω的值，运动时间将缩短，但会加大对大小鼠的刺激，同时搬运过程中的能耗也可能增加。因此对式(14)而言，不存在能够同时使3个目标函数都达到最优的全局最优解，只能从Pareto前沿解集中寻找满意解。

Deb等[14]在NSGA算法的基础上提出快速非支配排序遗传算法NSGA-II，用于解决多目标优化问题。NSGA-II算法引入精英策略，使优良个体在进化过程中得以保留，从而能够得到较优的结果，同时它还降低了NSGA的复杂性，具有运算速度快、解集收敛性好的优点。但是NSGA-II在交叉步骤采用的是模拟二进制交叉算子(Simulated Binary Crossover, SBX),该交叉算子在解空间中的搜索能力不强，存在可能无法搜索到非劣解的情况。张敏等[15]引入一个标准正态分布变量来替换SBX中的随机变量，既保持了与SBX算子相当的开发能力，又使新的交叉算子更加容易跳出局部最优，提高了其在解空间中的搜索能力。

正态分布交叉算子(Normal Distribution Crossover, NDX)可以描述为：设p1和p2为两个参与交叉的父代个体，c1和c1为两个子代个体，u为均匀分布在区间(0,1)内的随机数，N(0，1)为正态分布随机变量，则子代中的第i个变量按照式(21)～式(22)生成：

u≤0.5

(21)

u>0.5

(22)

基于正态分布交叉的NSGA-II算法流程如图4所示。

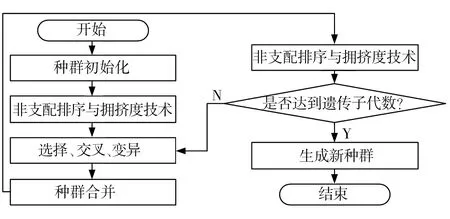
图4 基于正态分布交叉的NSGA-II算法流程

3 案例分析

3.1 参数设置

以某屏障环境中大小鼠自动化养殖线为研究对象，以搬运机器人在三维屏蔽养殖空间内的搬运运动参数A和ω为优化变量进行仿真实验，采用Matlab R2014b进行编程与算法验证。搬运机器人的运行参数设置如表2所示，搬运机器人5次作业的序列及其作业模式如表3所示。

表2 搬运机器人的运行参数

表3 搬运机器人作业序列及其模式

3.2 搬运机器人参数优化结果分析

(1)多目标优化算法有效性对比

为了验证所采用的NSGA-II算法的有效性与优越性，选择收敛性测度与多样性测度[16]这两个指标对本文算法与标准NSGA-II算法进行对比，两个测度的数值越小，表示优化结果的收敛性与多样性越好。对比验证选用标准测试函数Binh(2)，保证两组测试对象具有相同的参照系，使测试结果更加客观。两种算法对Binh(2)函数的收敛性测度与多样化测度计算结果如表4所示。

表4 收敛性测度与多样性测度计算结果

由表4可知，本文算法的两个测度值都小于标准NSGA-II算法的对应值，表明本文算法在解的收敛性与多样性上均优于NSGA-II，即采用本文算法更有可能快速地收敛到全局最优解。

(2)模型的Pareto解集与结果分析

按照表2、表3设定参数，利用基于正态分布交叉的NSGA-II算法求得式(14)的Pareto前沿解集(包含223个解)，如图5所示。

根据养殖企业对大小鼠品质要求以及养殖规模，进一步从图5中223个Pareto前沿解中筛选出符合养殖实际情况的满意解。首先，对于医学科研实验所使用的大小鼠而言，品质决定了其市场价格，高品质大小鼠与一般大小鼠的市场价格差异可达数十倍甚至数百倍，而大小鼠的品质高低与受到的应激刺激大小成反比，因此应使Aω2的值尽量小，以减少大小鼠的应激反应。其次，喂养大小鼠的鼠笼必须及时更换，否则鼠笼中的排泄物会滋生病菌，使大小鼠的品质降低，因此对于规模较大的养殖企业而言，搬运时间是仅次于搬运舒适度的优化目标。最后，减少搬运过程中的能耗有利于降低养殖企业的养殖成本，但是如果以降低大小鼠的品质为代价来降低养殖成本，养殖企业将会失去更大的销售利润，因此能耗目标是3个目标中最次要的。根据以上考虑，将Pareto前沿解集先按照加速度变化最小的目标进行升序排列，保留排列在前30%的解；然后，对保留下来的解集按照搬运时间最小的目标进行升序排列，保留排列在前30%的解；最后，再对保留的解集按照能耗目标最小进行升序排列并保留排在前10的解。经过这样筛选后得出的解集即为符合养殖企业需求的满意解，表5列出了排在前10的解及对应的优化目标值。

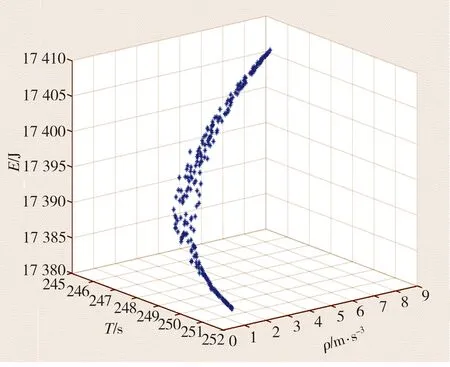
图5 采用基于正态分布交叉的NSGA-II算法获得的Pareto前沿解集

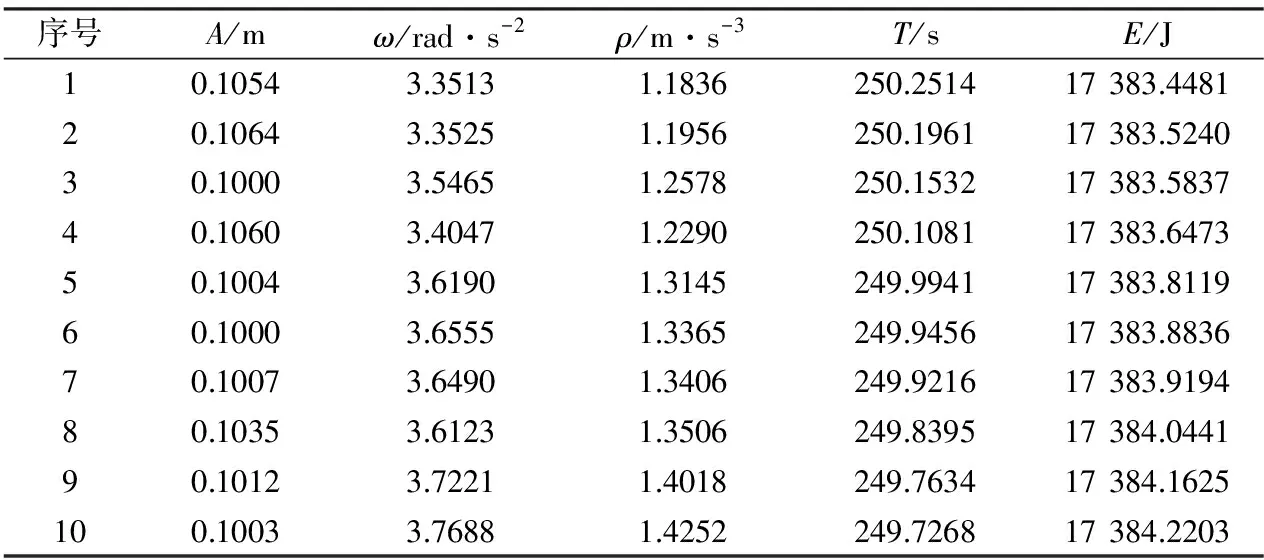
表5 排列前10的满意解及对应的优化目标值

如前所述，当加速度变化率小于1.5 m/s3时，大小鼠不会产生明显的不适感。在表5所列出的10组满意解中，加速度变化的最大值仅为1.4252 m/s3，能够满足在搬运过程中降低大小鼠的应激反应的要求。再从搬运总时间来看，由表5可知，搬运1个鼠笼的平均时间约为50 s，基本能够满足养殖企业将每个鼠笼的换笼时间控制在1 min之内的要求。上述案例证明了本文所提出的屏障环境中大小鼠养殖搬运机器人运动参数优化模型是合理的，能够较好地满足大小鼠养殖企业的实际需求，具有一定的应用价值。

4 结语

本文系统分析了屏障环境中大小鼠自动化养殖系统搬运机器人的参数优化问题，特别是针对运动参数对大小鼠造成的应激性刺激，建立了兼顾大小鼠舒适度、搬运时间与搬运能耗的多目标运动参数优化模型。针对该问题中各个优化目标之间相互冲突的问题，采用基于正态分布交叉的NSGA-II算法求取多目标优化模型的Pareto前沿解集，并根据养殖企业的实际需求从Pareto前沿解集中进一步挑选出能够使企业利益最大化的满意解。

本文在搬运机器人运动参数建模中，仅考虑了单机器人的情况。然而随着实验用大小鼠市场需求的不断增长，养殖企业的规模也在不断扩大，单机器人搬运可能无法满足对于换笼时间的要求，因此，屏障环境中大小鼠自动化养殖系统的多机器人协同运动参数优化问题将是下一步研究的重点。