移动局部约束结构模态特性分析

隋鑫 丁千 马之馨

摘要： 针对摩擦块?制动盘系统，研究移动局部约束?简化的环形梁结构的耦合系统动力学特性。采用非光滑基函数方法对系统降维求解，并引入线性弹簧代替局部约束。将环形梁偏微分方程转化为一组常微分方程，并结合移动载荷法的基本思想，分析移动局部约束结构的模态特性。结果表明：环形梁系统出现移动模态效应;局部约束使得模态函数出现局部峰值，剪力函数在局部约束处出现间断，同时表征载荷的位置。

关键词： 非线性振动; 局部约束; 移动模态; 非光滑基函数; 剪力

中图分类号： O322;O327 文献标志码： A 文章编号： 1004-4523（2021）05-0995-06

DOI：10.16385/j.cnki.issn.1004-4523.2021.05.013

引 言

摩擦块?制动盘耦合系统是高维非线性系统，尤其在考虑盘的弹性变形时，其振动方程为无穷维的偏微分方程，通常采用动力学降维的方法进行简化。典型的动力学降维方法包括线性和非线性Galerkin法、李雅普诺夫?施密特法（L?S法）、本征正交分解法（POD法）、基于规范性理论的中心流形法等[1]。

针对非线性系统，常采用POD与固定界面模态分析方法相结合，实现系统降维[2]。综合POD方法核心是把系统分成线性和非线性两种子结构，利用改进POD方法，用线性约束代替非线性成分，使得系统整体降维[3]，其前提是，经过泰勒展开后的非线性作用力产生的切向刚度矩阵，在弱非线性条件下近似为零。POD方法将相关函数正交分解，得到不相关的函数组，使得高维系统拥有较少模态[4]，该方法具有更高的收敛性，能够缩短计算时间。Lu等基于瞬态时间序列，采用近似流形的方法提出修正的POD方法，将多自由度的系统降维成两自由度，并保留了原有的动力学行为。通过比较，改进的POD解能够快速找到分岔点及检测分岔曲线和均方误差[5]。应用POD方法的计算量减少，但只适用于弱非线性系统，所以，改进方法的提出仍是局部约束系统的研究重点。

伽辽金方法适用于求解线性、非线性系统动力学方程，核心是将偏微分方程变换成一组常微分方程，系统方程可以被降维截断成前几阶响应的叠加，而忽视高阶响应的作用，伽辽金截断的依据是系统能量主要集中在低阶成分中。Barone等发现伽辽金模型的数值稳定性与投影内积的选择有关[6]。在求解柔性盘偏微分方程时，通过伽辽金方法降维得到的多个离散系统方程可以与振子单元的常微分方程（组）联立。Joe等采用标准伽辽金方法，考虑制动盘的正弦和余弦模态分析制动参数对系统的影响[7]。Ding等结合标准伽辽金方法和非线性伽辽金方法对转子系统进行求解，并比较两种方法的异同[8]。王晋麟等提出一种基于模态截断的改进非线性伽辽金方法，并将该方法与标准伽辽金法和非线性伽辽金法比较，总结了三种方法的有效性和适用性[9]。

非光滑基函数法作为求解局部非线性的新方法，结合了动力学降维的思想和传统伽辽金方法，对于非线性局部约束结构的求解具有精度高和快速收敛的特性。具体做法是采用线性弹簧代替局部连接处的非线性相互作用，并将与各阶模态正交化后的基函数补充到伽辽金解上[10]。Brake 等指出相对于标准伽辽金法得到的传统基函数，非光滑基函数方法需要较少的基函数实现收敛，而且计算速度更快。经过数值仿真和理论分析得出，含有局部约束的非线性系统的降阶模型是可行的[11]。非光滑基函数方法是对传统伽辽金法的一种补充。通过寻找局部约束刚度、正交化和归一化等一系列步骤，将产生的非光滑基函数补充到前几阶传统伽辽金振型，从而表征局部约束的位置和特点[12]。

目前，学者通常采用数值解法（主要是有限元法）和实验方法解决制动系统移动局部约束问题。Ouyang等研究发现，移动局部约束作用将导致系统产生较强的制动噪声;在低速情况下，盘?块耦合系统的接触表面载荷时变作用不容忽视;同时，制动盘振动响应受到在圆盘周向运动的移动刚性摩擦振子的影响[13]。Li等考虑接触表面力的时变特性，建立质量?阻尼?弹簧振子模型，研究柔性盘的横向振动;转速恒定时，圆盘面内出现摩擦引起的粘滑振动;而且盘与块在低速情况下出现分离?再接触现象[14]。

本文研究局部约束叠加系统的模态特性;考虑移动局部约束作用，建立移动局部约束?环形梁模型，采用非光滑基函数方法对系统降维，分析移动局部约束结构的模态和剪力特点。

1 移动载荷法

移动载荷法是指在求解过程中，考虑载荷的实时运动的方法。选取时间单位步长和空间位移步长。对于一个等份的系统：

a） 若，即在每个时间点，载荷恰好运动到下一离散点，不需分解载荷。同理，当（为某一正整数）时，即每时刻载荷恰好运动到另一离散点时，不需分解载荷;

b） 当（为速度）时，即载荷运动到相邻点和之间时，需要将细划分为等份。此时，每经过时刻，载荷运动。若运动到（）点（其中），此时需要将载荷分解，且分配到和處，点载荷大小为，而点载荷大小为，如图1所示。

2 非光滑基函数法

2.1 线性弹簧刚度选取

摩擦块与制动盘之间存在相对运动，接触位置存在局部载荷，根据非光滑基函数方法，可以采用线性弹簧（刚度为代替局部约束，由于制动盘的周向和径向的振动响应远小于外缘的横向振动，因此采用环形梁模型做简化模型，替代结构如图2所示。含有线性弹簧的运动表达式为

为式（1）中的左端项。其中，T为时间，X为环形梁轴向位置，ρ为环形梁密度，A为环形梁截面面积，E为环形梁弹性模量，I为环形梁截面转动惯量;δ为狄里克莱函数，V为局部约束轴向移动速度。以局部约束位置为分界，左端均为X[-L/2，L/2]上的响应函数。

选取线性弹簧刚度，过高的刚度值产生较小的幅值，而过低的刚度值很难准确表现出局部作用对振型的影响[10]。图3中，选取曲线中频率变化趋势出现转化拐点处的刚度值，即。

2.2 參考模态选取

通过时间和空间离散近似，响应函数可表示为

2.3 非光滑基函数形式

引入向量和的正交函数

3 局部约束叠加系统

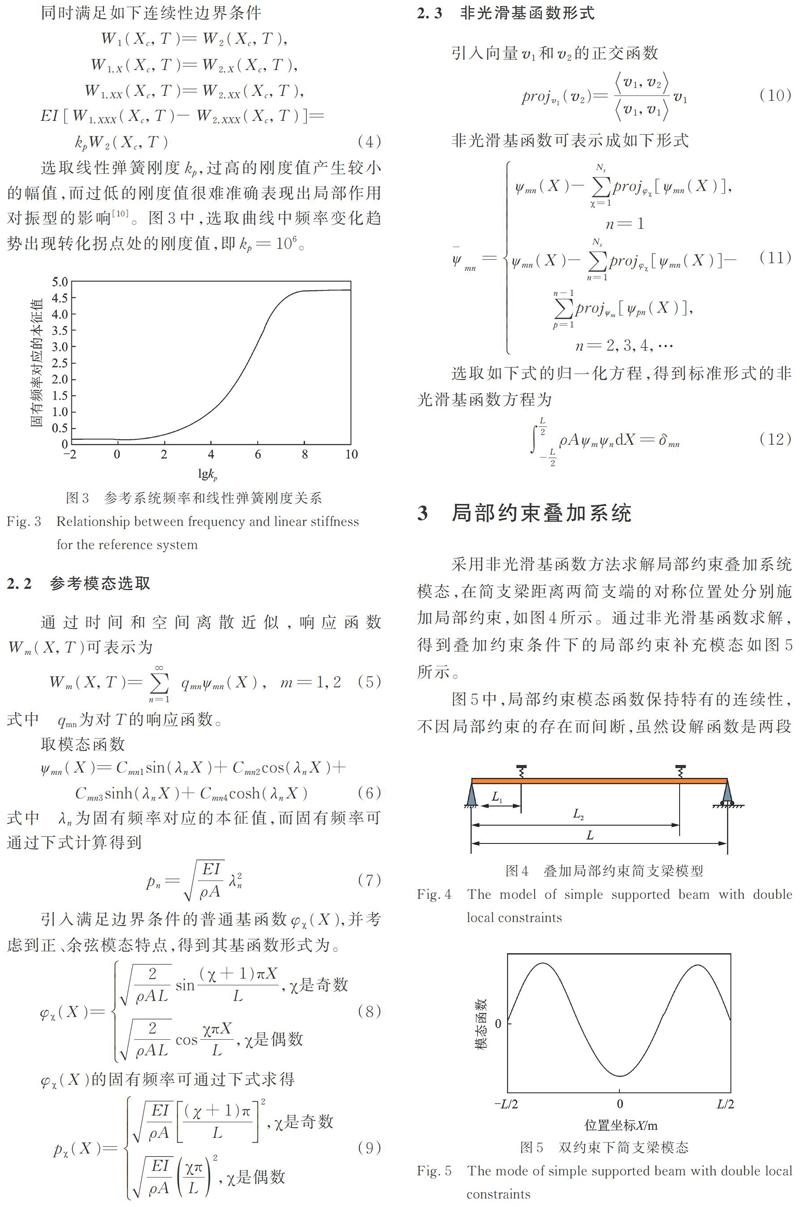
采用非光滑基函数方法求解局部约束叠加系统模态，在简支梁距离两简支端的对称位置处分别施加局部约束，如图4所示。通过非光滑基函数求解，得到叠加约束条件下的局部约束补充模态如图5所示。

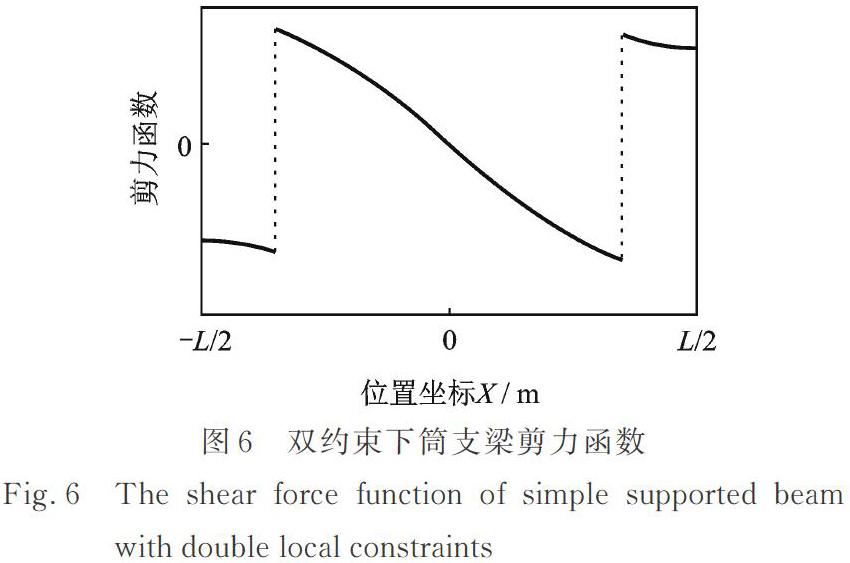
图5中，局部约束模态函数保持特有的连续性，不因局部约束的存在而间断，虽然设解函数是两段或是多段，但是模态都是连续的。图6中，剪力在局部约束处出现间断，能够反映局部约束的位置和大小，是对传统模态方法的改进。

4 移动载荷激励下环形梁的模态分析

4.1 模态频率求解

计算得到的环形梁前四阶频率本征值分别为，，和，如表1所示。表中，除零阶频率（平移和旋转频率）外，参考函数的频率本征值和普通基函数的值差异较小。此外，非零阶固有频率出现双频，即正弦模态频率和余弦模态频率。

通过数值解与试验值对比，除第二阶试验中存在弯扭耦合频率的影响外，其他阶次试验值与真实值之间的差异较小，验证了数值模型的准确性。

4.2 移动参考模态特性

根据模态函数（11），求出一阶移动载荷下的参考模态，如图7所示。水平轴表示随时间变化的移动局部约束位置。分析表明，制动盘横向振动模态随时间移动的特点明显，摩擦块与制动盘之间的接触力在移动区域（）内实时变化，曲线上的点表示载荷的位置。图8中，模态曲线在水平和竖直方向均成对称分布，而局部约束载荷出现在模态曲线的峰值处。图7中的移动参考模态特性与文献[15]中有限元结果相一致。

4.3 非光滑基函数模态

相比于普通基函数和参考基函数，非光滑基函数需要较少的模态就能达到收敛。图9为二阶非光滑基函数的模态和剪力。非光滑基函数对非线性不敏感，即得到的基函数不需要随非线性条件的变化而重新计算，因为派生的模态不依赖于含普通基函数的离散模态。

同样地，考虑移动载荷作用的平移模态和非光基函数的前三阶模态如图10所示，其中表示局部约束载荷位置。图中，实点和曲线分别代表载荷位置和移动模态。与参考模态相比，叠加模态曲线的峰值恰好在载荷位置处。经分析，非光滑基函数法的主要特点为模态函数的连续和剪力函数的间断，无论模态函数还是剪力函数，载荷位置都很明显。因此，非光滑基函数是对参考模态的补充。

此外，非光滑基函数模态相对于水平方向非对称，模态函数的突出位置与剪力曲线的不连续部分对应的水平坐标一致。与普通基函数和参考模态函数相比，非光滑基函数更适合求解局部约束问题，可以清晰表达移动载荷的位置。

5 结 论

本文研究了移动局部约束?简化的环形梁结构的耦合系统动力学特性。提出移动载荷法的基本思想，并应用非光滑基函数方法对移动局部接触作用的环形梁系统降维，计算分析其模态特性。

1） 环形梁模型计算的固有频率与试验解相近，验证了模型的正确性;

2） 局部约束结构具有以下特点：模态函数连续和剪力不连续;

3） 移动载荷作用下的环形梁出现移动模态效应，与有限元结果一致;

4） 模态函数和剪力函数都能表征局部约束载荷位置，即模态曲线中出现局部峰值位置和剪力曲线间断位置对应的水平坐标。

参考文献：

[1] 于 海， 陈予恕. 高维非线性动力学系统降维方法的若干进展 [J]. 力学进展， 2009， 39（2）： 154-164.

Yu Hai， Chen Yushu. Recent developments in dimension reduction methods for high-dimension dynamical systems[J]. Advances in Mechanics， 2009， 39（2）： 154-164.

[2] 尉 飞， 郑钢铁. 利用POD方法的固定界面模态综合技术 [J]. 振动工程学报， 2008， 21（4）： 365-370.

Wei Fei， Zheng Gangtie. Fixed-interface component mode synthesis using proper orthogonal decomposition[J]. Journal of Vibration Engineering， 2008， 21（4）： 365-370.

[3] 赵松原， 黄明恪. POD降阶算法中对基模态表达的改进 [J]. 南京航空航天大学学报， 2006， 38（2）： 131-135.

Zhao Songyuan， Huang Mingke. Modification to basic modes of reduced order model for computing airfoil flow field[J]. Journal of Nanjing University of Aeronautics and Astronautics， 2006， 38（2）： 131-135.

[4] 谢 丹， 徐 敏. 基于特征正交分解的三维壁板非线性颤振分析 [J]. 工程力学， 2015， 32（1）： 1-9.

Xie Dan， Xu Min. Three-dimensional panel nonlinear flutter analysis based on proper orthogonal decomposition method[J]. Engineering Mechanics， 2015， 32（1）：1-9.

[5] Lu K， Yu H， Chen Y， et al. A modified nonlinear POD method for order reduction based on transient time series [J]. Nonlinear Dynamics， 2014， 79（2）： 1195-1206.

[6] Barone M F， Kalashnikova I， Segalman D J， et al. Stable Galerkin reduced order models for linearized compressible flow[J]. Journal of Computational Physics， 2009， 228（6）： 1932-1946.

[7] Joe Y G， Cha B G， Sim H J， et al. Analysis of disc brake instability due to friction-induced vibration using a distributed parameter model[J]. International Journal of Automotive Technology， 2008， 9（2）： 161-171.

[8] Ding Q， Zhang K. Order reduction and nonlinear behaviors of a continuous rotor system [J]. Nonlinear Dynamics， 2011， 67（1）： 251-262.

[9] 王晋麟， 曹登庆， 宋敉淘. 大型动力系统的降维：基于模态截断的非线性Galerkin方法 [J]. 动力学与控制学报， 2009， 7（2）： 108-112.

Wang Jinlin， Cao Dengqing， Song Mitao. Dimensional reduction of large dynamical systems：An nonlinear galerkin method based on model trunction[J]. Journal of Dynamics and Control， 2009， 7（2）： 108-112.

[10] Segalman D J. Model reduction of systems with localized nonlinearities[J]. Journal of Computational and Nonlinear Dynamics， 2007， 2（3）： 249-266.

[11] Brake M R， Segalman D J. Modelling localized nonlinearities in continuous systems via themethod of augmentation by non-smooth basis functions[J]. Proceedings of the Royal Society A-Mathematical Physical and Engineering Sciences， 2013， 469（1）： 1-20.

[12] 李金錄， 丁 千. 局部约束结构振动的模态研究[J]. 振动与冲击， 2015， 34（4）： 98-103.

Li Jinlu， Ding Qian. Modal approach for vibration of a structure with local constraints[J]. Journal of Vibration and Shock， 2015， 34（4）： 98-103.

[13] Ouyang H， Mottershead J E， Li W. A moving-load model for disc-brake stability analysis [J]. Journal of Vibration and Acoustics， 2003， 125（1）： 53-58.

[14] Li Z， Ouyang H， Guan Z. Friction-induced vibration of an elastic disc and a moving slider with separation and reattachment [J]. Nonlinear Dynamics， 2016， 87（2）： 1045-1067.

[15] Kang J. Automotive brake squeal analysis with rotating finite elements of asymmetric disc in time [J]. Journal of Sound and Vibration， 2017， 393（1）： 388-400.

作者简介： 隋 鑫（1992-），男，博士，工程师。E-mail：xsui@tju.edu.cn