聚焦核心素养 重视综合实践 提升数学阅读

【摘 要】 近年来，数学中考越来越重视学生综合能力的考察，也是大环境下中考命题的新趋势.就2021年苏州数学中考第27题而言，考察了三维空间中的注水追及问题，通过对该试题的分析与思考，提出初中数学教学应指向学生数学核心素养的发展、重视综合实践活动的价值、培养数学阅读能力.

【关键词】 数学核心素养;综合与实践;数学阅读;中考数学

近年来，数学中考越来越关注学生综合能力的考察，这是在重视素养发展背景下的命题趋势.正如2021年苏州数学中考的第27题，它推陈出新，舍弃了完全以动点为背景的数学综合题，而是以向长方体容器中注水的水位变化问题替代.在此题中，繁琐的过程说明让学生望而却步，仔细阅读后发现，此题是披着注水问题外衣的追及问题，难度不大，但其指明了初中数学教学的育人方向.

1 试题呈现

2021年江苏省苏州市中考数学卷第27题：

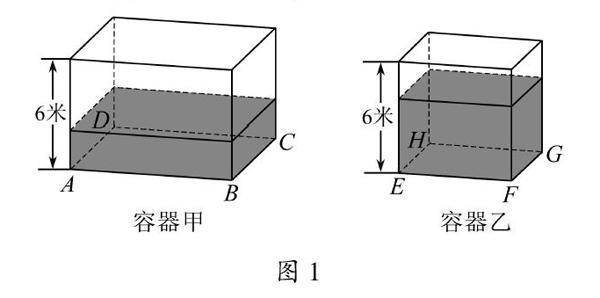
如图1，甲、乙都是高为6米的长方体容器，容器甲的底面ABCD是正方形，容器乙的底面EFGH是矩形.如图2，已知正方形ABCD与矩形EFGH满足如下条件：正方形ABCD外切于一个半径为5米的圆O，矩形EFGH内接于这个圆O，EF=2EH.

（1）求容器甲、乙的容积分别为多少立方米？

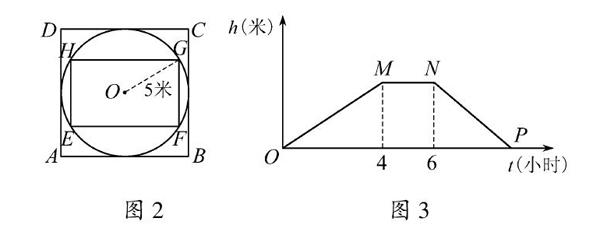
（2）现在我们分别向容器甲、乙同时持续注水（注水前两个容器是空的），一开始注水流量均为25立方米/小时，4小时后，把容器甲的注水流量增加a立方米/小时，同時保持容器乙的注水流量不变，继续注水2小时后，把容器甲的注水流量再一次增加50立方米/小时.同时容器乙的注水流量仍旧保持不变，直到两个容器的水位高度相同，停止注水.在整个注水过程中，当注水时间为t时，我们把容器甲的水位高度记为h甲，容器乙的水位高度记为h乙，设h乙-h甲=h，已知h（米）关于注水时间t（小时）的函数图象如图3所示，其中MN平行于横轴.根据图中所给信息，解决下列问题：

①求a的值;

②求图3中线段PN所在直线的解析式.

2 试题分析与思考

第一小问主要利用圆的相关知识及勾股定理求解.第二小问的含义是向两个底不同的长方体容器中注水，对于容器乙而言，注水速度始终保持25立方米/小时不变，容器甲注水速度在前4个小时内保持25立方米/小时，而后速度增加a立方米/小时，即以（25+a）立方米/小时的速度注水，使得两容器液面高度差始终一致，2小时后，继续加快注水速度至（75+a）立方米/小时，直至两容器液面相平.

就第二小问求解而言，难度不大，只需要抓住题目的两个关键点，即：“两容器液面高度差始终一致”和“两容器液面相平”.对于“两容器液面高度差始终一致”而言，就是一个巧妙的等量关系，学生可以在4到6小时内，任意选取两个时间来表示两容器液面的高度差，建立一个一元一次方程，进而得到a的值.而后“两容器液面相平”更直白地呈现了一个等量关系，即点P横坐标所对应的时间是甲、乙两容器液面相等的时刻，进而又可以得到一个一元一次方程，求解出点P的具体坐标，再结合点N的坐标，可以很快得出线段PN所在的直线解析式.

追本溯源，此题就是一类三维的追及问题.在初中阶段，学生更多接触到的是二维追及问题.但此题推陈出新，在二维追及问题的基础上加入了一个定量，即不同的底面积，将问题向三维的视角下推进，但究其本质，这类问题的解决方式是异曲同工的.

其实该试题并非聚焦于知识的考察，而是更关注学生在问题解决中数学素养与能力的体现.如：对于问题、图象的理解与抽象就是最典型数学抽象能力的应用;构建高度差h与时间t的函数或者建立一元一次方程的过程就是数学建模素养的体现;还包括数学运算、直观想象等素养的渗透.除了数学核心素养，像数学阅读能力、数形结合思想也都能在该问题的解决中展现出来.

3 试题求解

问题（1）求解：易得容器甲底面边长为10米;容器乙底面长为45米，宽为25米.故容器甲的容积是600立方米，容器乙的容积是240立方米.

问题（2）求解：①当t=4时，h=h乙-h甲=4×2540-4×25100=1.5，即M（4，1.5）.

又由于MN平行于横轴，所以N（6，1.5）.

当t=6时，h=6×2540-4×25+2（25+a）100=1.5，解得a=37.5.

②解法一：方程思想.

设经过t1小时两容器水位高度相同，可得25t140=25×4+62.5×2+112.5（t1-6）100，解得t1=9，即P（9，0）.

设线段PN所在直线的解析式为：h=kt+b.

将N（6，1.5）和P（9，0）代入h=kt+b，得到1.5=6k+b，0=9k+b.  解得k=-12，b=92.

所以线段PN所在直线的解析式为：h=-12t+92.

解法二：“k”的实际意义.

设线段PN所在直线的解析式为：h=kt+b.

由题意：线段PN所在直线的解析式中k的实际含义是两容器注水速度与其底面积比值之差，即k=2540-112.5100=-12.

因此，将N（6，1.5）代入h=-12t+b，得到1.5=-12×6+b，解得b=92.

所以线段PN所在直线的解析式为：h=-12t+92.

4 教学启示

4.1 教学更应指向学生数学核心素养的发展

数学的学习一方面在于数学知识的掌握，另一方面指向数学核心素养的习得与发展.在立德树人为教育根本任务的大背景下，数学核心素养培养更是如今教学的重中之重.近年来，数学中考越来越关注学生素养的考察.正如此题中，对于问题的理解并抽象出容器甲、乙的注水速度与水位变化的数学关系是对学生数学抽象能力的考察，如果学生数学抽象能力薄弱，根本不能提取出注水速度与水位的变化关系，那么更别去谈求解此题.数学研究的对象就是源自于人类对于现实生活的抽象的东西，在此类基于现实背景的数学问题更注重数学抽象能力的考察.此外，在此题中，像h与t函数的构建、利用方程求解a的值，都是考察学生能否提炼出问题中的等量关系并用数学符号建立方程来表示，即数学建模素养.在数学模型的求解中，也涉及到数学运算等素养的考察.综上所述，中考试题对于数学核心素养的考察是综合性的，渗透于解题的各个环节之中.

数学核心素养的培养任重道远，需要教师抓住契机、巧妙渗透、潜移默化.以数学抽象素养的培养为例，在数学学习中，数学概念是数学学科的“灵魂”，是中学数学教学的重点.数学概念在历史的长河中沉淀，大多都拥有着丰富的历史底蕴，其产生大多是数学抽象的结果.教师在概念教学的过程中，必然会引导学生观察具体实物，提取本质属性，抽象获得概念，因此概念的教学是数学抽象素养培养的“温床”.在初中阶段，学生认知水平不高，所学习的数学内容相对浅显，对于数学内容的表述大多停留于生活语言，而未上升至符号语言.所以，在初中阶段存在的数学抽象大多是浅层次的，多数停留于半符号化阶段.对此教师应重视数学抽象素养的培养，积极抓住适合培养数学抽象素养的数学概念，在概念的形成中体验数学抽象的过程，渗透数学抽象的方法，并在课后练习和综合实践活动中巩固与运用，多形式地发展学生的数学抽象能力.

4.2 重视综合实践活动的价值

“综合与实践”作为《义务教育数学课程标准（2011年版）》的一大特色与“数与代数”等并列为数学四大课程内容.“综合与实践”是以问题为载体、以学生自主参与为主的数学活动[1].该内容强调综合性与实践性，综合性是指所研究问题广泛、包含的数学知识全面、涉及的学科多样、学生的素质综合提升;实践性强调学生在教师的引导下主动参与，体现“過程”.“综合与实践”是学生主动思考、积极探究、讨论合作、实践操作的重要平台，也是创新精神与应用意识培养的重要载体.不妨深入思考该题，不难发现，此题的本质即为三维的追及问题.以此题为背景的九年级综合实践活动可以从二维追及问题出发，呈现如下的问题1，让学生在熟悉的动点问题中探索函数解析式与具体问题之间的关系，为上述中考题的探究求解铺垫.

问题1：如图4，射线OM上有一点A，满足OA=20cm，点P和点Q分别从点O和点A出发，沿OM方向，一开始均以1cm/s的速度匀速运动，4秒后，点P的速度增大acm/s，同时点Q速度不变，继续运动2秒后，再次将点P的速度增大3cm/s，同时点Q速度不变，直到两点相遇，运动停止.在运动过程中，当运动时间为t时，我们点P到点O的距离记为s1，点Q到点O的距离记为s2，设s2-s1=s.根据所给信息，解决下列问题：

（1）若a=1.5，尝试绘制出s（cm）关于运动时间t（秒）的函数图象.

（2）若s（cm）关于运动时间t（秒）的函数图象如图5所示，求a的值和线段EF所在直线的解析式.

思考：观察线段DE和线段EF所在直线的解析式，两条直线的“k”有什么实际含义？

问题1的第一小问旨在引导学生去读题、提取关键的数学信息，进而让学生在绘制出函数图象的过程中，理解图象上各个点的具体含义，积累数学抽象的经验，也为第二小问提供解题思路.在学生自主探究完问题1后，教师可以给出问题2——2021年苏州数学中考第27题，逐步引导学生从二维向三维飞跃.在问题2的解决中，教师可以指出两个问题之间的联系，并让学生思考图象中一次函数的“k”的具体含义，两个问题中的“k”之间的差异在哪？学生通过对两个问题的比较与分析，透过现象直击问题本质，充分理解问题的内涵.

随后，教师可以进一步激发学生思考：如果将正方体的容器换为其他立体图形，如：圆柱、三棱锥等，水位高度的变化、注水速度与注水时间之间存在什么关系呢？如图6所示，以正三棱锥OABC为例，已知其高为H米，△ABC的面积为S，注水速度为a立方米/秒，注水时间为t秒，水位高度记为h米，则可以得到h=H-3H3-3atH2S，

图6若将正三棱锥OABC倒置，则可以得到h=33atH2S.虽然在三棱锥等锥形的几何图形中，水位高度会出现三次根号，不适合在考试中呈现，但是学生在探究的过程中，其数学建模、数学运算、直观想象等数学素养得到了提升，也为今后高中的学习打下坚实的基础.

4.3 击破“畏难”心理，培养数学阅读能力

数学阅读能力是指学生能够通过数学化的分析，从数学材料提取数学信息，形成自我的数学观点.数学阅读是一种内在的心理过程，需要经历提取信息、数学建模和数学表达三个阶段[2].对学生而言，题目越简洁，越敢于去尝试.但面对像该题数行的过程说明，以及考试限时的大环境下，学生难免会出现“畏难”心理，将题目的长短与问题的难易联系起来，形成刻板印象，进而部分学生连题目都不愿意去阅读.同时也有部分同学虽阅读了题目，但其完全没有理解题目的含义，究其原因，一方面，可能是学生自身的数学知识水平还未达标，另一方面，可能归咎于数学阅读能力的薄弱，无法提取关键信息服务于问题的解决.

因此，在日常教学中，教师首先要打破学生的刻板印象，将其头脑中“怕麻烦”“不想做”等惰性思维扼杀，让学生形成不畏难、不退缩、不妥协的学习品质，在遇到诸如此类题目时，不怕困难，敢于去读题尝试.而后，教师应该教会学生数学阅读的方法，让学生在教师的指导下，能够完全提取出题目中所给的有效条件，并在完备的知识体系下，快速地挖掘出各个条件所带来利于解题的新条件.教师在问题的分析中，应多让学生思考“题目中有什么条件”“这些条件能得到什么新条件”“新旧条件中有哪些是利于解题的”等问题，促使学生在会解题的基础上，促进理解题目的内涵、形成自己的解题方法、获得自身能力与素养的全面发展.

参考文献

[1]中华人民共和国教育部制定.义务教育数学课程标准（2011年版）[M].北京：北京师范大学出版社，2012：5.

[2]孙俊勇.谈数学阅读[J].基础教育课程，2020（2）：42-46.

作者简介

黄贤明（1999—），男，江苏苏州人，中学二级教师，研究方向：初中数学教学研究.