精推细敲 突出本质 彰显素养

【摘 要】 几何作图以开放发散的思路、几何直观的方式、思维严谨的逻辑成为数学教学中蕴含思维价值的教学内容.一道好的作图试题，从初步构想到最终定稿乃至到考后反思稿的命制过程中，需要对试题文本和结构进行精雕细琢，深度思考，以达到以下目的：经历精推细敲，实现科学评价;回归教材文本，考查核心知识;关注学生现实，凸显育人价值;彰显思维品质，引领教学导向.

【关键词】 几何作图;无刻度直尺;命题研究

尺规作图作为一种常规的试题类型受到试题命制者的青睐，相较于尺规作图，仅用无刻度直尺完成作图的试题表现出工具更为弱化、思维含量更高的特点.此类试题融入更多的核心知识和理性思考，工具方便、操作简单，更能考查学生对几何知识的掌握与灵活运用，有利于考查学生思维的逻辑性、知识的关联性、能力的综合性等数学素养.笔者在命制本区九年级检测试题时，将倒数第三题以无刻度直尺作图的方式呈现，现将本题的命题构想、历程及思考呈现如下.

1 命题构想

根据试卷的双向细目表的安排，第25题是全卷倒数第3题，满分为8分，难度系数0.4，试题创新命题形式，尝试舍去常用的网格图背景，探索无网格图背景的无刻度直尺作图，以“关注核心知识，凸显数学素养”为基本立意，基于保持整份试卷的结构稳定及试题风格，具体构想如下：（1）问题设计以学生熟悉的核心几何知识为载体，蕴含丰富的数学思想方法，着重考查数学素养和创新能力;（2）试题灵活考查轴对称图形变换的性质;（3）试题要源于教材，表述简洁，兼顾基础性和区分度，突出考查直观想象和逻辑推理等核心能力.

2 命题历程2.1 初始稿：原以为很美

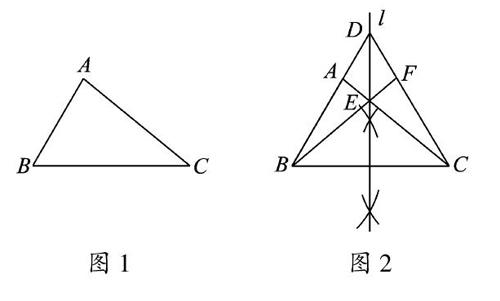
如图1，已知△ABC，分别按下列要求作出图形.（不写画法，保留作图痕迹）

（1）用直尺和圆规画出线段BC的垂直平分线l.

（2）只用无刻度的直尺，画出点A关于直线l的对称点.

解答 （1）如图2;（2）如图2，直线l与AC交于点E，连接BA并延长交直线l于点D，连接CD，连接点BE并延长交CD于点F，点F即所求.

诊断 第1问很基础，并且为第2问铺垫，梯度比较合理，区分度较好.第2问并没有重复考查“对称轴是对应点所连线段的垂直平分线”的性质，而是进而考查学生灵活运用“两个图形关于某条直线对称，如果它们的对应线段或延长线相交，那么交点在对称轴上”的性质来构图，注重理性思维水平的考查.

细细品味，初稿有明显不足.首先，两问的作图工具并不一致，显得刻意，不和谐自然;其次，要求画出点A的对称点，呈现的△ABC不仅显得多余，而且线段AB、AC对于第2问有明显的提示作用，弱化了灵活运用轴对称性质来有序构图的思维含量.于是剥离出初稿中的无关因素，只呈现更为本质的要素，打磨成改进稿.2.2 改进稿：自以为真美

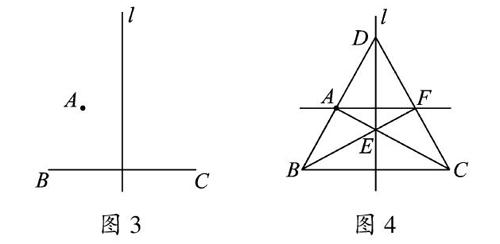
如图3，直线l是线段BC的垂直平分线，点A是直线l外一点，位置如图所示.只用一把无刻度的直尺，过点A作BC的平行线并证明.（不写作法，保留作图痕迹）

解答 如图4，连接AC交直线l于点E，连接BA并延长交直线l于点D，连接CD，连接点BE并延长交CD于点F，作直线AF即所求.

证明方法省略.

诊断 改进稿的呈现兼具严谨性和简洁性，除了考查学生的作图能力，在完成证明的过程中进一步考查逻辑推理能力.第1问的作图不仅摒弃了无关因素的影响，而且将直白的作对称点改进成过直线外一点作已知直线的平行线，这样“一点两线加垂直”的试题呈现极其简约，然而，简约而不简单，与试题简洁的呈现形成鲜明对比的是作图探究背后蕴含的思维价值.本题作AF∥BC本质就是作AF⊥l，作AF⊥l只需作点A的对称点，那如何用无刻度直尺作对称点，需要又一次调用另一条轴对称的性质来理性构建图形，突出考查学生从观察图形、追溯源头、探析作法、完成构图经历的完整探究过程.第2问的作图证明涉及到“图形与几何”领域的全等三角形、相似三角形、等腰三角形、线段垂直平分线、平行线的判定和性质等核心知识，证明方法多样，对学生逻辑推理能力的要求较高.

改进稿突出考查了学生的几何直观和逻辑推理的能力，美中不足的是两问都对学生的思维要求较高，难度较大，对于几何作图中逻辑推理能力的考查超出了课标的要求，作为一道区域性的统测试题，显然不合适，于是再次精推细敲，反复斟酌，从而形成审定稿.2.3 审定稿：当时觉得美

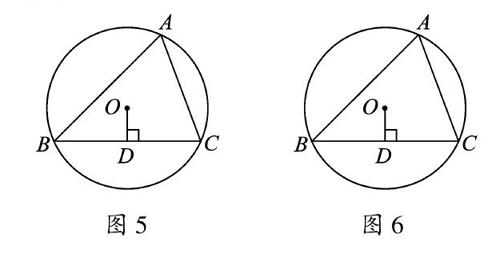
已知⊙O是△ABC的外接圆，过点O作OD⊥BC，垂足为D.

（1）在图5中，只用无刻度的直尺，画出△ABC的角平分线AE.

（2）在图6中，只用无刻度的直尺，过点A作AP∥BC，并说明理由.

解答 （1）如图7，延长OD交⊙O于点E，连接AE交BC于点F，AF即所求.

（2）方法1 如图8，延长DO交AB于点E，连接CE并延长交⊙O于点P，作直线AP即所求.证明：由OD过圆心，OD⊥BC，得BD=CD.即OD是BC的垂直平分线.所以EB=EC.可得∠B=∠BCE.又∠B=∠APC，可得∠BCE=∠APC，所以AP∥BC.

方法2 如图9，分别延长CA、DO交于点F，连接BF交⊙O于点P，作直线AP即所求.证明：由OD过圆心，OD⊥BC，得BD=CD.即OD是BC的垂直平分线.由FB=FC.可得∠FBC=∠C.又因为四边形PBCA是圆内接四边形，所以∠FPA=∠C，可得∠FBC=∠FPA，所以AP∥BC.

方法3 如图10，连接BO、CO分别交⊙O于点F、G，连接GA交直线OD于点H，连接FH并延长交⊙O于点P，作直线AP即所求.證明略.

诊断 反复斟酌后，引入圆的背景，并将“一点两线”恢复成初始稿的△ABC，继续探究平行线的作法，增加第（1）问作三角形的角平分线.圆是重要的轴对称图形，它的自然融入不但可以容易构造新的点，有效降低难度，同时也很好地考查圆中相关核心知识.无论作三角形的角平分线，还是作平行，都需要学生关联圆中核心知识，有序构建基本图形来解决问题.

圆背景的融入还使作平行线的方法由单一变得多样化，作平行线的关键是运用轴对称的性质，明确了对称轴的突出地位，确定对称轴的三种方法也应运而生.因为对称轴上可以利用的对称线段的所在直线的交点有3个，分别是图8，9，10中的E，F，H.其中，方法1正是利用圆的对称性将作图由原来的连5条线减少为2条，更为简洁又不失理性思考，同时作法的证明难度由于圆的核心知识的运用比改进稿有显著降低.

经历试题的精雕细琢，最终审定成稿，并顺利地进行了统测.通过试题批改的数据反馈，虽然试题的难度和区分度都达到了预期，但细细品味，反复琢磨，总觉意犹未尽.首先，第1问的作图难度还是有点大，得分率不高;其次第2问的作图和证明的难度很接近，有重复考查之嫌，没有层层递进，平行的作法探析过程本身就对逻辑推理有很好的考查，而作法证明与前者并无明显的区别.最后，两问之间没有很强的逻辑关系，整体性和系统性也不够，基于统测的数据分析，对审定稿又进行了改进，最终形成反思稿.2.4 反思稿：实现真的美

如图11，已知⊙O是△ABC的外接圆，过点O作OD⊥BC，垂足为D.只用无刻度的直尺，你能过点A画出△ABC的哪些特殊线段？请画出这些线段.（不写作法，保留作图痕迹）

解答 过点A可以画出△ABC的中线、角平分线、高.如图12，连接AD即△ABC的中线;如图13，延长OD交⊙O于点E，连接AE交BC于点F，AF即△ABC的角平分线.

作高的方法1 如图14，延长DO交AB于点E，连接CE并延长交⊙O于点F，连接FO并延长交⊙O于点G.连接AG交BC于点H，AH即△ABC的高.

作高的方法2 如图15，连接AO并延长交⊙O于点F，连接CF交OD的延长线于点E，连接BE交⊙O于点G.连接AG交BC于点H，AH即△ABC的高.

诊断 在本试题讲评教学时，学生提出如何作高的问题，这引发笔者的进一步思考.最终形成的反思稿中，第（1）问的作中线面向全体学生，有效降低了难度，第（2）、（3）问作角平分线和高，层层递进，很好地解决了审定稿中重复考查的问题，同时也使整道题形成前后连贯、逻辑一致、一以贯之的特点，对学生聚焦图形结构，直观想象和逻辑推理的能力进行了充分的考查.

3 命题思考

3.1 经历精推细敲，实现科学评价

本试题的命制以无刻度直尺作图灵活考查轴对称变换的性质为目标，以科学评价和引领教学为价值取向，从试题初始稿到反思稿的打磨历程紧紧围绕呈现方式、问题设计、试题结构、考查维度、难度系数、形式创新等方面精雕细琢，反复打磨.命题历程中有左冲右突的煎熬，更有柳暗花明的畅快.呈现方式上脱胎换骨，但考查目标却始终一以贯之;能过点A画出△ABC的哪些特殊线段的问题设计更加突出整体和开放的视角，层层铺垫，螺旋上升，凸显思维进阶;试题结构由审定稿的牵强拼凑变得关联性更强，逻辑清晰，更利于学生从系统性和整体性高度理解数学本质，避免了碎片化;考查维度也逐渐优化，关注了学生分析问题、捕捉有效信息的能力，类比归纳已有作中线、角平分线的活动经验形成新的经验综合运用到作高中的迁移能力，以及面对开放型新颖试题镇定自若的心态和创新能力;改进稿作为试题，其难度系数过大，显然超出了学生的“最近发展区”，会挫伤学生的信心，基于以生为本的价值取向需要再打磨降低难度.

命题者要不断追求科学命题，突出数学本质，彰显数学核心素养，积极导向立德树人的课堂教学，同时让师生共同意识到试题就源于教材，来自课堂，着重考查通性通法和思维品质，而大量刷题作业是高耗低效的，为切实减轻学生作业负担做好命题评价方面的正确引领.3.2 回归教材文本，考查核心知识

教材是课堂教学的重要依据和资源，也是保证试题符合课程标准的衡量标准.本试题的初始稿就是以苏科版教材的例题为素材，在作图工具和试题结构上做了两点改编创新，使试题源于教材，但又不拘泥于教材.因此，试题的命制素材来源于以课标为依据的教材例题、习题，再进行加工、整合、拓展;也可以来源于鲜活的课堂教学的生成，将学生在活动探究和思维碰撞中迸发的精彩的问题融入命题之中.

同时，试题命制要关注学生对核心知识的掌握和数学本质的领悟.初中阶段数学的核心知识是形成数学能力提升数学素养的重要载体和抓手，也是命题者青睐的对象，综合数学的核心知识，进行命题，有利于考查学生的数学素养及探究能力，有助于从知识考查走向能力立意[1].本题聚焦初中数学的核心知识有：轴对称、垂直平分线、平行线性质、垂径定理、等弧所对的圆周角相等、直径所对的圆周角是直角等核心知识.

3.3 关注学生现实，凸显育人价值

在命制试题时，要关注学生现实，学生现实不仅包括数学知识水平，思维能力和解题经验，而且包括数学实际生活背景与数学活动经验[2].因此，在命题中应充分重视和关注学生的个体差异，以学生发展为本.比如反思稿中设计的画三角形的中线、角平分线、高，三个问题层层递进，贴近学生已有的学习经验，大部分学生“跳一跳能摘到”.试题的价值不能仅限于知识、能力的判定，更要着眼于每个学生的发展和人的价值.

试题命制要体现数学学科育人的价值，要用试题背后的数学思想和理性精神滋养学生，让学生像数学家那样思考解决问题，引导学生经历数学知识发生、发展和应用的全过程[3].反思稿开放性的活动设问，注重了对学生数学活动过程的考查，激发了学生的好奇心和求知欲，引发学生深入探索和思考.用无刻度直尺作三角形重要线段，循序渐进、螺旋上升、一以贯之，很好地考查了学生数学活动过程中所表现出来的思维方式、思维水平.3.4 彰显思维品质，引领教学导向

试题命制要减少机械记忆试题和客观性试题比例，提高探究性、开放性、综合性试题比例.这是教育部《关于加强初中学业水平考试命题工作的意见》所要求的.反思稿的问题设计充满开放性、探究性，试题以开放发散的思路、几何直观的方式、思维严谨的逻辑来彰显思维的灵活性和深刻性.考查学生根据目标图形的特征逆向分析、调用核心知识、构造图形，凸显“分析”的思路，通过逻辑推理、类比归纳来追溯源头、探析作法，同时揭示“对称”的本质，感悟蕴含在作图过程中的对称思想，从而掌握知其然（怎么作图），知其所以然（这样作的道理），何由以知其所以然（怎么想到这样作）通性通法[4].

试题考查的目标和要求对教师的教和学生的学具有鲜明的导向作用，试题命制应该导向教师积极探索基于情境、问题导向、深度思考，高度参与的教育教学方式[5].反思稿中蕴含丰富的教学资源，在教学中，教师应以学定教，顺学而教，通过分步适时的点拨加追问，激发学生经历主动关联调用相关核心知识，并将其整体化、经验化、结构化，理性构建基本图形来获取解决问题思路的全过程，体验感悟了作法背后的“理”与“法”，潜移默化地达到了深度学习，发展学生发散性思维、几何直观、数学推理能力等数学素养.因此，试题命制者要注重以测导教的功能挖掘充分发挥试题的教学导向功能，以试题为载体，导引教师将培养学生的数学核心素养放在首要位置.

参考文献

[1]陶家友.关注基础凸显核心[J].中国数学教育，2019（12）：51-55.

[2]臧铁生.教育考试与评价[M].北京：中国青年出版社，2020：14-15.

[3]张丹，王彦伟.数学学科育人指向：用数学思想和理性精神滋养学生[J].中小学管理，2019（11）：9-11.

[4]章飛.三个基本作图的方法思辨与教学实施[J].中学数学教学参考（中旬），2021（7）：2-5.

[5]吴增生.初中数学毕业考试命题变革的思考与实践[J].数学通报，2021（1）：41-51.

作者简介 陶家友（1981—），男，中学高级教师，南京市学科带头人，江苏省教科研先进个人，江苏省卓越教师培养对象，南京市溧水区数学名师工作室主持人，主要研究课堂教学与中考命题.