美英早期几何教科书中的等腰三角形性质与判定
2021-12-16钱秦汪晓勤
钱秦 汪晓勤
【摘 要】 选取1800—1959年间出版的103本英美早期几何教科书,研究发现教科书中关于等腰三角形性质——“等边对等角”的证明方法共有六种,即欧几里得的方法、帕普斯的方法、勒让德的方法、莱斯利的方法、作高法和实验操作法.而关于等腰三角形判定定理——“等角对等边”的证明方法共有七种,即欧几里得的反证法、想象有两个三角形、大边对大角、作顶角角平分线、作底边的高、做底角的角平分线和实验操作法.早期教科书中的等腰三角形知识,为今日教学提供了丰富素材.
【关键词】 等腰三角形;等边对等角;等角对等边;美英早期教科书
1 引言
在平面几何中,三角形的“等边对等角”“大边对大角”“等角对等边”“大角对大边”是对三角形边角关系的定性刻画,是三角学中边角定量关系的基础.在西方数学史上,《几何原本》卷一命题5(等腰三角形底角相等)是一个著名的几何定理,被称为“驴桥定理”,既因为欧几里得在证明该定理时所用的图形像一座简单的桁架桥,也因为它阻挡了许多中世纪的学习者进一步学习《几何原本》后续命题的脚步.
关于等腰三角形的性质和判定,我国现行五种初中数学教材(人教版、北师大版、沪教版、浙教版及苏教版)的内容安排大同小异.在引入上,五种教材均设计了折纸活动;在“等边对等角”的证明上,人教版和北师大版教材通过作底边的中线,利用SSS定理加以论证,而沪教版和浙教版教材通过作顶角的平分线,利用SAS进行说理,而苏教版教材除折纸验证外,并未给出具体的说理过程.关于“三线合一”性质,浙教版教材设计了以“几何画板”为工具的探究活动,而另四种教材均通过“等边对等角”加以说理.关于“等角对等边”,北师大版教材仅仅作辅助线的提示而未给出完整的证明,其余四版教材均通过作顶角平分线,运用AAS定理进行说理[1-4].已有的教学设计大多从教材出发,通过剪纸、折叠引入新课,个别教师运用了数学史.
不难发现,关于等腰三角形的性质与判定,现行教科书倾向于作辅助线(中线、角平分线)来构造全等三角形,但这几种方法的合理性受到人们的质疑.如,在《几何原本》中,SSS定理(命题I.8)的证明用到了三角形的唯一性(命题I.7),而三角形唯一性的证明又需要用到“等边对等角”(命题I.5),这就使得涉及SSS定理的证明具有循环论证之嫌.而角平分线(命题I.9)的存在性又要用到SSS定理,使得作角平分线的合理性也得不到保证[1].鉴于此,我们聚焦等腰三角形性质与判定,对19世纪初至20世纪中叶的美、英几何教科书进行考察,试图回答以下问题:关于等腰三角形的性质与判定,早期几何教科书中采用了哪些证明方法?证明方法有何演变规律?对今日课堂教学有何启示?
2 教科书的选取
本文从有关数据库中选取1800—1959年间出版的103种美英早期平面几何教科书作为研究对象,其中85种出版于美国,18种出版于英国.在选取的过程中,对于同一作者再版的书籍,若相关内容无明显差异,则视为同一种;若内容有明显差异,则视为不同的教科书.以20年为一个时间段,各教科书的分布情况如图1所示.
早期几何教科书的章节划分不像今天一般细致清晰,有的教科书甚至未划分章节,直接以一个个命题的形式呈现.103种几何教科书中,等腰三角形主题所在章节主要有“命题”“直线形”“三角形”“等腰三角形”“线、角与直线图形”“全等三角形”等.表1为具体分布情况.我们也发现,无论章节名如何,本节内容在各教材中所處的位置都比较靠前.由此可以说明,等腰三角形的性质与判定是平面几何的一个基础内容.
等腰三角形的性质主要有“等边对等角”和“三线合一”,但大部分教材中,“三线合一”并未给出论证,而是将其作为“等边对等角”的推论直接给出.判断一个三角形是否为等腰三角形时,可以根据定义,也可通过“等边对等角”来判断.因此,本文将从“等边对等角”和“等角对等边”两个角度梳理早期教科书中的证明方法.
3 “等边对等角”的证明
考察发现,在103种教科书中,有2种只提示学生作辅助线,通过三角形全等进行证明,但未给出完整的证明过程;101种教科书给出了完整的证明,证明方法大致可分为6类:欧几里得的方法、帕普斯的方法、勒让德的方法、莱斯利的方法、作高法、实验操作法.
3.1 欧几里得的方法
欧几里得的伟大贡献在于公理化体系的建立,其《几何原本》从给定的少数公理、公设及定义出发,用逻辑推论方法推导了四百多个命题[2].“等边对等角”作为《几何原本》第一卷命题5,其证明过程严格遵循公理化体系,只用到了命题5之前的公设、公理及命题.
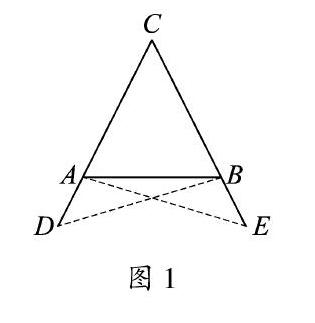
有10种教科书沿用了欧几里得的证明.如图1,在等腰△ABC中,CA=CB.在两腰CA和CB的延长线上取两点D,E,使得AD=BE,并连接AE和BD,则CD=CE.由SAS定理,可证△CAE≌△CBD,故有∠CAE=∠CBD;再由SAS定理,可证△BAE≌△ABD,故有∠EAB=∠DBA.根据“等量减等量,差相等”,得∠CAB=∠CBA[3].
3.2 帕普斯的方法
11种教科书采用了古希腊数学家帕普斯(Pappus,公元3世纪末)的方法:将等腰三角形△CAB和△CBA看作两个三角形,然后用SAS证明△CAB≌△CBA.
也许有人会认为,把一个三角形看作两个三角形,对学生来说较为抽象,于是把另一个三角形“外化”出来了.如图2,已知等腰△ABC,CA=CB.想象△ABC被拿起、翻转后放下,记作△A′B′C′(A′,B′,C′分别对应A,B,C).那么,AC=A′C′=BC=B′C′,则在△ABC和△A′B′C′中,AC=B′C′,BC=A′C′,且∠C=∠C′.根据SAS定理有△ABC≌△B′A′C′,则∠A=∠B′,又因为∠B=∠B′,等量代换得∠A=∠B[4].
3.3 勒让德的方法
法国数学家勒让德(A. M. Legendre,1752—1833)通过作底边中线的方法来构造全等三角形,从而得到“等边对等角”.有4种教科书采用他的方法.如图3,在等腰△ABC中,CA=CB.过点C作底边AB的中线CD.由SSS定理可证△CAD≌△CBD,则∠A=∠B[5].
3.4 莱斯利的方法
苏格兰数学家莱斯利(J. Leslie, 1766—1832)的方法有69种教科书采用.如图4,在等腰△ABC中,CA=CB.过顶点C作∠BCA的角平分线,交AB于点D.根据定理SAS可证△ACD≌△BCD,故得∠A=∠B[6].
3.5 作高法
4种教科书采用作高法.给定CA和CB为等腰△ABC中相等的两边,作CD⊥AB交AB于点D,如图5.在Rt△CAD和Rt△CBD中,CA=CB,CD=CD,根据HL定理,可证△CAD≌△CBD,所以∠A=∠B[7].
3.6 实验操作法
有5种教科书采用了实验操作(折叠).如图6所示,通过尺规作图构造一个等腰△CAB,小心地将三角形从纸上剪下.沿底边AB的中线将三角形折叠,并比较∠CAB和∠CBA的大小.接着再构造不同尺寸的等腰三角形,同样比较两个底角的大小.我们观察到,等腰三角形的底角是相等的[8].
3.7 证明方法的演变
19世纪初至20世纪中期,早期教科书中呈现了丰富的方法来解决这个问题.以20年为一个时间段,图7给出了“等边对等角”的六种证明方法在每个时间段的分布.
由图7可见,在考察的整段时间,教科书用来说明“等边对等角”的方法呈现多元化的特点,但始终以莱斯利的作角平分线方法为主流.欧几里得延长两腰的做法,由于其严密的逻辑及在几何上的独特地位,使它在两千多年后的教科书中仍占有一席之地.帕普斯的方法,巧妙地将三角形对应的部分重合,在历史上流行了很长一段时间.但随着更简便的作辅助线(角平分线、底边中线及高)证明三角形全等的方法出现,欧几里得和帕普斯的方法逐渐淡出了历史舞台.到了20世纪,实验几何开始受到人们的重视,一些教科书相应设计了折纸的实验操作来丰富学生的直观体验.
那么,是否如引言中提到的质疑一样,一些证法存在着逻辑上的漏洞呢?今天,人们对“等边对等角”某些证法的质疑主要依据的是《几何原本》的体系.然而,本文所考察的美英早期几何教科书采用了不同的逻辑体系,不同的逻辑体系就造成了知识点编排顺序的差异.勒让德在《几何基础》中采用了图8所示的命题顺序[5],SSS定理并未建立在等腰三角形性质之上,他通过作底边中线来证明“等边对等角”,是完全合理的.莱斯利则采用了图9所示的命题顺序[6],其通过作角平分线证明“等边对等角”,也是严谨的.
4 “等角对等边”的证明
“等角对等边”,即如果三角形中有两个角相等,那么其对边相等,这个三角形为一个等腰三角形.83种教科书给出了完整的证明,证明方法大致可分为以下7种.
4.1 欧几里得的反证法
23种教科书沿用了欧几里得的反证法.如图10,令∠CAB=∠CBA.假设对边AC比另一边BC要长,令AD=BC,那么△DBA明显要比△ABC小.但因为CB与BA及其夹角∠CBA等于DA与AB其夹角∠DAB,故知△DAB≌△CAB,这是不可能的(大小不同的三角形不全等).因此,AC不能比BC長.类似可证明BC不能比AC长,所以BC=AC[9].
4.2 想象有两个三角形
11种教材采用“想象两个三角形”的方法.如图11,给定△ABC,其中∠A=∠B.假设△A′B′C′是△ABC的一个复制品,将△A′B′C′翻转后放在△ABC上,那么B′将落在A上,A′将落在B点,则B′A′与AB重合.因为∠A′=∠B′,∠A=∠A′,等量代换得∠A=∠B′,所以B′C′将与AC重合.类似地,A′C′将与BC重合.因此,C′将同时落在AC和BC上,即C′落在它们的交点C上.所以,B′C′=AC.又有B′C′=BC,则AC=BC[10].
4.3 大边对大角
6种教科书先证明“大边对大角”,再由此说明“等边对等角”.如图12,给定△ABC,其中∠A=∠B,以下三个命题中必有一个是正确的:(1)a=b,(2)a 4.4 作底边上的高 27种教材采用作底边的高的方法.如图13,给定△ABC,其中∠A=∠B.作CD⊥AB,那么在两个直角△CAD和△CBD中∠A=∠B,所以∠ACD=∠BCD.因此,△CAD和△CBD中有两个角及其夹边CD对应相等,由ASA定理知△CAD≌△CBD,则AC=BC[12]. 4.5 作顶角的平分线 11种教科书中采用作顶角平分线的方法.如图13,在△ABC中∠A=∠B.作∠ACB的平分线CD,易证△CAD≌△CBD,故AC=BC[13]. 4.6 作底角的平分线 有2种教科书采用作底角角平分线的方法.如图14,给定△ABC,其中∠ABC=∠BAC.作BD平分∠ABC,AE平分∠BAC,由ASA定理知△DBA≌△EAB,从而∠BDA=∠AEB,所以∠CDB=∠CEA,且BD=AE,又∠C=∠C,故△ACE≌△BCD,故得AC=BC[14]. 4.7 实验操作法 3种教科书采用剪纸、折叠的方式来验证“等角对等边”,证明过程与“等边对等角”的类似,这里不再赘述. 4.8 证明方法的演变 图15给出了“等角对等边”的各种证明在各时间段的分布情况. 由此可见,19世纪80年代之前“欧几里得的反证法”占有绝对优势,而后“作底边的高证三角形全等”成为使用频率最高的方法.欧几里得的方法十分经典,只用到SAS定理,一度受到人们的青睐.但作底边的高后无需分类讨论,能通过一次三角形全等解决问题,相比之下证明过程更加简便.“大边对大角”“实验操作”“想象有两个三角形”和“作顶角的角平分线”等,都只是在少数几个时间段内零星出现的方法. 奇怪的是,20世纪40年代涌现了一种新的方法,即“作底角的角平分线”证两次三角形全等,从证明过程来看,该方法不如前面的大部分方法简便,但它却被20世纪40年代的教科书所采用.这看似较为复杂的证法,恰恰体现了数学家们不懈探究、追求创新的精神. 5 结论与启示 “等边对等角”与“等角对等边”是历史悠久的两个命题,在两千多年的历史长河中,涌现了许多优秀的证明方法.这些证明方法相继出现于本文所考察的103种早期几何教科书中.遗憾的是,我们在今天的教科书中却几乎看不见它们的踪影.美英早期几何教科书中的证法各有特色,关于“等边对等角”的证明,“莱斯利的方法”在各教科书中占绝对优势.而关于“等角对等边”的证明,“欧几里得的反证法”在相当长的时期内都是主流方法,但到了19世纪80年代以后,“作底边上的高”后来居上,而欧氏方法逐渐退出了历史舞台. 美英早期几何教科书为HPM视角的等腰三角形教学提供了一定的启示. (1)营造探究之乐.本节内容可采用探究式学习的模式,设计不同大小等腰三角形的折纸活动,引导学生归纳出等腰三角形的性质.通过体验性极强的折纸活动,学生能提高学习兴趣,让数学课堂活起来.接下来,教师则可以利用几何画板等现代工具对学生的猜想加以检验.在定理的证明上,先由学生自主探究其证明方法,再由教师进行讲授,使学生充分参与到课堂中来. (2)彰显方法之美.无论是“等边对等角”还是“等角对等边”,早期教科书都呈现了丰富的证明方法.这些来自不同时空的灵活、多样的方法,能够拓宽学生的视野.教科书上呈现的一两种推导方法是远远不够的,教师应该对历史上的多种证明方法进行介绍.而且,数学知识毕业后不用就很快遗忘了,但排除法、反证法等思想对学生来说却是受益终身的.因此,教学不能仅局限于证明过程本身,更重要的是让学生掌握证明背后蕴含的思想方法. (3)实现能力之助.“等边对等角”与“等角对等边”互为逆命题,要判断这两个命题的真假必须分别对其进行严格的证明,这对于培养学生的逻辑推理能力有着极大的帮助.同时,课堂上安排折纸的实验操作,也有利于学生直观想象素养的发展. (4)达成德育之效.一方面,教学过程中可以讲述“驴桥”的故事,告诉同学们中世纪时期人们学习几何也同样会遇到挫折,让学生们得到安慰,使数学变得不那么可怕.另一方面,通过折纸活动感知“等边对等角”后进一步说明论证的安排,使学生明白數学是一门严密的学科,任何内容的学习不能仅停留在直观.数学家们不懈探究、追求创新的治学态度,在早期几何教科书对等腰三角形性质与判定定理的证明中体现得淋漓尽致.相信学生们通过本节内容的学习,能够树立正确的数学观,培养理性精神. 参考文献 [1]汤雪川,栗小妮,孙丹丹.“等腰三角形的性质”:从历史中找应用,看证明[J].教育研究与评论(中学教育教学),2018(11):52-61. [2]杨虹霞,胡永强.问题驱动 以史为鉴 探究知识 解决问题——HPM视角下“等边对等角”教学实录与反思[J].上海中学数学,2020(12):39-43. [3]张青云.既见树木,又见森林——对“等腰三角形的性质与判定”一课的设计与思考[J].中国数学教育(初中版),2019(11):58-61. [4]刘建.一次“单元教学”的实践与思考——以“等腰三角形的性质与判定”为例[J].中学数学,2016(2):30-32. [5]唐小勃.谈数学教材证明等边对等角的方法不合理的原因[J].数学学习与研究,2018(8):134-135. [2]何红英.从欧几里得《几何原本》谈公理化思想[J].西安文理学院学报(自然科学版),2018,21(06):11-13. [3]Hunter T.Elements of Plane Geometry[M]. New York.: Harper & brothers, 1872. [4]Halsted G B. The Elements of Geometry[M]. London: Macmillan, 1886. [5]Legendre A M.Elements of Geometry [M]. Edinburgh: Oliver & Boyd, 1822. [6]Leslie J S.Elements of Geometry [M]. Edinburgh: James Ballantyne and Co., 1809. [7]Wells W.The Essentials of Geometry (plane)[M]. Boston: D.C. Heath & Co., 1901. [8]Baker A. Elementary Plane Geometry [M]. Boston: Ginn &Company, 1903. [9]Young J R.Elements of Geometry [M]. London: J. Souter, 1827. [10]George W, Smith D E.Plane Geometry[M]. Boston: Ginn and Company, 1913. [11]Slaught H E, Lennes N J. Plane Geometry [M]. Boston: Allyn and Bacon, 1918. [12]Brooks E. Plane Geometry[M]. Philadelphia: Christopher Sower Company, 1901. [13]Milne W J. Plane Geometry[M]. New York: American Book Company, 1899. [14]Major G T.Plane Geometry[M]. Exeter: Edwards Brothers, 1946. 作者简介 钱秦(1999—),女,重庆人,华东师范大学教师教育学院硕士研究生,主要从事数学史与数学教育研究.汪晓勤(1966—),男,浙江衢州人,教授,华东师范大学教师教育学院博士生导师,主要从事数学史与数学教育研究.
