基于FCM的簇内欠采样算法

刘稀文，段隆振，段文影

(南昌大学信息工程学院，江西 南昌 330031)

分类技术一直是机器学习和数据挖掘领域的研究重点和热点，在理论研究和工程实践领域都有着广泛的应用。传统的分类算法如KNN、SVM和决策树等在平衡数据集上通常表现很好，但在样本类别分布不均衡时，会出现分类面偏倚的现象，少数类的样本更容易被误判，得不到好的分类结果。例如，网络入侵检测[1]、信用卡欺诈检测[2]、垃圾邮件过滤[3]、自闭症诊断[4]等问题就是典型的类别不平衡问题，在互联网入侵检测的样本数据中，入侵的样本数远远少于正常的样本数，如果将传统的分类器直接应用于这些类别不平衡的样本上，模型会倾向于多数类，忽略少数类样本，从而降低了对少数类样本的分类能力，甚至会出现把全部样本都判为多数类的情况，这样的分类结果是没有意义的。针对类别不平衡的分类问题，已有很多有效的算法被提出，主要体现在两个层面：算法层面和数据层面。

算法层面是对标准的分类算法进行改进，或者提出新的应用在不平衡数据集上的分类算法。算法层面典型的解决方法有代价敏感算法和集成学习方法。代价敏感学习[5]是在训练模型时以整体误分代价的最小化取代样本的整体误差最小化作为训练目标，通过引入代价矩阵，赋予少数类样本更大的代价权重，以降低分类器在少数类样本上的错分率。集成学习方法的思想是将多个基分类器组合成一个强分类器，以提高分类性能。集成学习有两种经典的范式：Bagging[6]和Boosting[7]。

数据层面主要包含过采样和欠采样算法。过采样方法中最简单的是随机过采样，但这种方法容易导致过拟合。Chawla等人[8]提出了少类样本合成过采样技术(synthetic-minority-over-sampling-technique，SMOTE)，根据样本分布对少数类别样本进行分析模拟，在少数类样本的邻域间插入人工合成的新少数类样本，在一定程度上避免了随机过采样法易于陷入过拟合的问题。此外还有在SMOTE算法基础上进行了改进的Borderline-SMOTE[9]算法、ADASYN[10]算法等。

在欠采样方法中，最简单的方法是随机欠采样(Random Under Sampling，RUS)，随机删除多数类中的部分样本，形成新的平衡数据集。但这种方法存在随机性，容易删除一些有代表性的样本数据，导致多数类样本丢失一些重要信息，分类器不能学习到完整的分类规则。为了克服这一缺点，很多研究者都提出了其他的欠采样方法。Zhang等[11]提出基于KNN的4种欠采样方法：NearMiss-1，NearMiss-2，NearMiss-3和MostDistant。思路是利用K近邻信息挑选具有代表性的多数类样本，实验表明NearMiss-2算法具有较好的不平衡数据的分类能力。李春雪等人[12]使用聚类算法，令每次聚类的簇数取不同的值，对多数类样本进行多次聚类，把聚类中心作为新的多数类样本参与训练，提高了分类结果的G-mean值。但该方法需要生成很多份不同不平衡比率的训练集，然后在这些训练集上分别训练分类模型，其时间复杂度较大。Kocyigit 等人[13]使用FCM算法对全部样本进行聚类，得到若干个簇，重复进行50次聚类，每次聚类指定不同的簇数，选择与聚类中心最近邻的多数类样本加入候选集，然后用t检验从候选集中选出与少数类样本相等数量的多数类样本，与少数类样本合并得到平衡的训练集。该算法提高了分类器的分类性能，而且算法的独立性较好。Lin等人[14]提出了两种基于聚类的欠采样方法：Clustering-based undersampling(CBUS)，令多数类的聚类簇数等于少数类样本的个数。 在方法1中，对样本中的多数类使用kmeans聚类算法，将聚类中心作为新的多数类样本与少数类样本合并，得到新的平衡样本集，此类方法较为经典，其它的研究人员[15]也使用了这种方法。在方法2中，先对多数类样本进行kmeans聚类，然后选择每个聚类中心的最近邻样本作为新的多数类样本与少数类样本合并。这两种方法都有效地改善了传统的分类算法在不平衡数据集上的分类效果。但此类方法也存在一些不足，不能保证聚类簇数等于少数类样本数时的G-mean值一定最大，而且如果少数类的样本非常多，则要求多数类的簇数也要同样多，聚类的时间会相应地成倍增加。另外，这些方法只是考虑了类间不平衡问题，没有考虑到类内不平衡问题。

为了克服传统分类器在不平衡数据上的性能缺陷，本文借鉴基于聚类的欠采样方法，结合模糊聚类和集成学习理论，提出基于FCM的簇内欠采样算法(Fuzzy C-means clustering based undersampling in clusters)，提高不平衡数据的分类性能。

1 相关工作

1.1 模糊 C-均值聚类算法(Fuzzy C-means

clustering，FCM)

在聚类问题的研究工作中，研究者应用均方逼近理论构造带约束的非线性规划函数，将聚类问题的求解转化为非线性目标规划问题，此时的目标函数是类内平方误差和J1。Dunn[16]基于模糊划分理论把每个样本与全部聚类中心的距离用其隶属度平方加权，把J1推广到类内加权平均误差和函数J2。后来，Bezdek等人[17]引入参数m，把J2推广到一个目标函数的无限簇，并提出了交替优化算法，形成了FCM 算法。

FCM算法的优化目标函数是：

(1)

其中，D是样本总数，N是聚类簇数，uij表示元素xi对第j类的隶属度，cj是第j个簇的簇心，m是权重指数，控制着聚类矩阵的模糊程度，m的值大于1，且m越大，聚类的模糊程度越高，m越小，则聚类越接近于硬C均值聚类。在实际应用中，m的缺省值为2。

FCM 算法的算法步骤如下:

初始化：设X是由d个元素构成的集合，X={x1，x2，…，xd}，给定聚类类别数N，2 ≤N≤d，迭代停止阈值ε，初始聚类中心C0，迭代计数器b=0；

步骤1用下式计算或者更新划分矩阵Ub=Uij：

(2)

步骤2根据公式(3)更新聚类中心Cb+1：

(3)

步骤3如果‖Ub+1-Ub‖≤ε或者算法达到指定的迭代次数，则算法停止并输出划分矩阵和聚类中心，否则令b=b+1，转为执行步骤一。

1.2 K近邻(k-nearest neighbor，K-NN)分类器

KNN算法[18]是一个广泛使用的分类算法，其思路是：对于某个待分类的样本，若在该样本的K个最近邻的样本中大多数属于某个类，就将该样本判为这个类别。关于k值的选择，一般令k为较小的奇数，可以采用交叉验证法来确定。样本间的距离通常选用欧式距离、曼哈顿距离、马氏距离、余弦距离、汉明距离等公式来度量，本文使用欧氏距离。对于两个样本A、B，假设A=(x1，x2，…，xn)，B=(y1，y2，…，yn)，则它们之间的欧氏距离为：

(4)

1.3 随机森林(Random Forest，RF)

构建随机森林的算法步骤如下：

算法1随机森林的构建算法

输入：训练集N，训练集N的总数n，随机森林的规模k，每个决策树选择的特征数m。

输出：随机森林分类器RF。

1.初始化：RF=∅；

2.Fori=1:k

3.使用Bootstrap抽样法对训练集N重复n次抽样，得到第i个决策树treei的训练集Ti和treei的袋外样本OOBi；

4.在训练集Ti上随机选择m个特征，训练决策树treei；

5.使用treei对OOBi进行预测；

6.将第i棵决策树纳入RF模型，RF=RF∪treei。

7.End for

随机森林算法具备了Bagging 算法与随机子空间算法的特点，能很好地处理在训练模型时可能存在的特征遗失现象，由于样本随机和特征随机的二重随机性，模型不易陷入过拟合，而且由于袋外数据的存在，使用袋外数据可以在建模的过程中得到真实误差的无偏估计，不需要另外留出验证集对模型进行评估，袋外数据误差估计与同训练集一样大小的测试集得到的精度一样，可以用袋外误差估计取代测试集的误差估计。

2 基于FCM的簇内欠采样算法

2.1 相关概念

不平衡数据集是指在数据集中不同类别的样本在数量上具有很大差别的数据集。其中，样本数较多的一类样本被称为多数类样本，也叫负类样本，样本数较少的一类样本称为少数类样本，也叫正类样本。多数类样本数与少数类样本数之比称为不平衡比率(imbalanced ratio，IR)。数据集的IR值越大，分类难度也就越大。为了降低数据集的不平衡比率，需要以合适的采样倍率对数据集进行重采样，采样倍率是一个系数，例如少数类(或多数类)样本的数量为m，采样倍率为n，则重采样后的少数类(或多数类)样本数为m*n。

2.2 算法过程

基于FCM的簇内欠采样算法(Fuzzy C-means clustering based undersampling in clusters，FCMUSIC)主要有两个过程：首先，利用 FCM算法对多数类样本进行聚类欠采样 ，设定聚类簇数n的值，n的选择通过层次聚类算法初步确定，然后用交叉验证法尝试比较多个n值。在得到聚类划分的n个簇后，对每个簇进行欠采样，在每个簇内，按照采样倍率不放回地随机抽取一定数量的样本代表多数类，得到新的多数类样本，和少数类样本合并，形成平衡样本集。其次 ，在得到的平衡数据集上训练分类器 ，并进行多次分类实验。本文在欠采样后的平衡数据集上结合单个分类器和集成分类器进行训练，以检测在不同的分类器上的提升效果。

FCMUSIC在欠采样阶段的算法描述如下：

算法2FCMUSIC算法

输入：不平衡数据集S，聚类簇数n。

输出：平衡数据集S′。

1.初始化：S′=φ；

2.将数据集S划分为多数类N-和少数类N+，计算数据集S的不平衡比率IR；

3.使用FCM算法将多数类样本N-划分为n个簇，N-={C1，C2，…Cn}；

4.Fori=1:n;

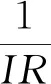
6.S′=S′∪Di；

7.End for

8.返回S′。

关于聚类簇数n的值，本文使用层次聚类算法来进行选择。层次聚类可以把数据划分到不同的组群，聚类的结果是树状结构， 可以被直观地展示出来，然后人为地观察来确定聚类的簇数。关于层次聚类的更多介绍可以参阅文献[19]。层次聚类的结果如图1所示，每个子节点上的数据可以被分到同一个簇。

图1 层次聚类的结果可视化

数据不平衡不仅体现在多数类与少数类之间的比例不平衡，也体现在同一类别的数据内部。如图2所示，多数类样本分布在major1和major2两个不同的区域，major2是小析取项。这两个区域互不相邻，而且在样本数量上也有很大的差异。major2偏离样本空间太远，却又与少数类样本空间相邻，而且包含的样本数量稀少，容易被当成噪声样本处理，或者被直接忽略，导致没有利用到这部分样本的信息。FCMUSIC算法对多数类样本进行聚类可以找出小析取项的簇，然后在这些簇内抽样，避免出现小析取项样本没被利用的情况。

图2 样本集的类内分布

FCMUSIC算法减少了多数类样本的数量，获得了平衡的训练集。原始不平衡样本集和经过FCMUSIC算法处理后的样本集的样本分布分别如图3和图4所示。其中，类别1为多数类，类别2为少数类。FCMUSIC算法在每个簇内都选取了一定数量样本，使得抽取的样本来自于原始样本集分布空间的各个方向，保留了多数类样本原有的分布特征，从而在保证了欠采样后样本的多样性和全面性。

特征2图3 原始样本分布

特征2图4 经FCMUSIC算法处理后的样本分布

3 实验分析

3.1 实验数据集

为了检验FCMUSIC算法的分类性能，选取UCI(https://archive.ics.uci.edu/ml/index.php)和KEEl(http://www.keel.es)上的五组不平衡数据集进行实验，分别是pima、yeast1、haberman、segment0和German Credit Data(以下简称german)。5组数据的具体信息如表1所示。

表1 5组数据的具体信息

3.2 实验环境

实验环境为64位Windows10 操作系统，Intel Core i5处理器，8GB内存，512G固态硬盘，开发工具使用开源软件R3.6.0。

3.3 实验评价指标

性能评价测度是对模型分类效果的一种量度，最为常用的一个测度就是分类正确率，即为分类模型对测试集样本分类正确的数量与测试集样本总数之比。对于平衡数据集的分类，分类正确率可以很好地反映出模型的性能，但在不平衡的数据集上，就很难反映出模型的性能高低。假设有一个包含100个样本的数据集，有90个属于多数类样本和10个少数类样本，分类器只要把这个数据集全部判别为多数类就能保证90%的正确率，但是很显然，这样分类没有识别出少数类样本，分类表现非常差。因此，对于不平衡数据集，需要采用其它的性能测度来反映分类模型的质量。被广泛采用的性能测度有查准率Precision 、召回率Recall 、真正率TPR、F-measure，G-mean和 AUC值。

在二分类问题中，分类器对样本的分类结果有四种情况，通过混淆矩阵展示，如表2所示。

表2 二分类问题的混淆矩阵

根据模糊矩阵，可以计算出对于分类器的性能测度：

分类精度的计算如公式(5)所示：

(5)

分类器的查准率Precision:

(6)

召回率Recall：

(7)

真负率：

(8)

F1度量是对Precision和Recall两者的一种平衡，如果分类器分类后的Precision和Recall都比较高，F1才会比较高。

(9)

真正率TPR和真负率TNR代表分类器在正类与负类样本各自的分类精度，G-mean可以来平衡这二者的关系：

(10)

G-mean是TPR和Recall的几何均值，如果TPR很大但TNR很小，或者TNR很大TPR很小，G-mean都不能取得较大的值，只有当TPR和TNR都较高的时候，G-mean才能取得较大的值，因此，G-mean能较为全面地评价分类器的性能。

ROC 是以假正率 FPR 为 x 轴 ，真正率 TPR为 y 轴绘制的曲线。AUC即为ROC曲线下的面积。AUC 值常用于评价分类器性能，如果AUC值越高，代表着分类器的分类效果越好 。本文采用F1、G-mean、AUC 3种度量作为分类器的评价指标。

3.4 实验结果分析

为了验证FCMUSIC算法的综合性能，采用原始数据直接建模、随机欠采样算法RUS、CBUS1算法作为对比组，使用KNN分类器、RF分类器结合欠采样处理后的平衡数据集进行分类，并设置以下对比组，分别是：不经处理的原始数据、经随机欠采样算法(RUS)处理后的数据、文献[14]中的第一种基于聚类的欠采样算法CBUS1处理后的数据(CBUS1算法对多数类样本应用kmeans聚类，并设置聚类簇数等于少数类样本数，将聚类中心作为欠采样后的多数类样本)。然后结合KNN分类器和RF分类器进行分类。KNN的临近数k值通过交叉验证法来选择，先根据经验指导，选择比较小的奇数作为k值，然后进行交叉验证，最终选择分类结果最好的情况下使用的k值。

关于聚类簇数n的选择，先使用层次聚类初步确定n可能的取值，观察得到适合的一个或多个值作为待选的n值，然后把多数类样本按照不同的n值进行聚类，选择使分类表现较好的n值。聚类簇数n对实验结果的影响较大，以pima数据集为例，当聚类簇数取不同的值时，F1、G-mean和AUC的值如图4到图6所示。聚类簇数n值的范围是从2到少数类样本数。从图中可以看出，随着n的增加，F1和G-mean值呈现下降趋势，AUC的变化总体平缓。在本实验中，数据集pima、yeast1、haberman、segment0和german各自的n的取值为：8、27、5、3和9。

聚类簇数图5 不同聚类簇数下的F1值

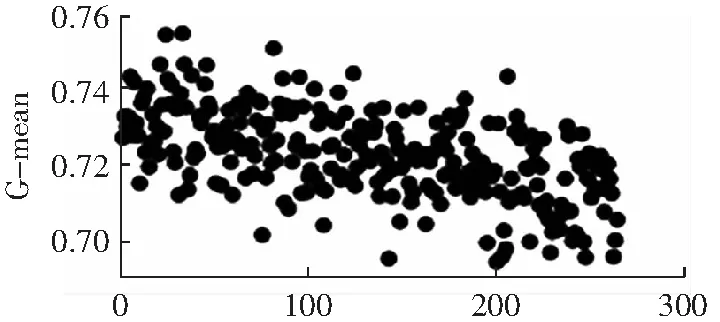
聚类簇数图6 不同聚类簇数下的G-mean值

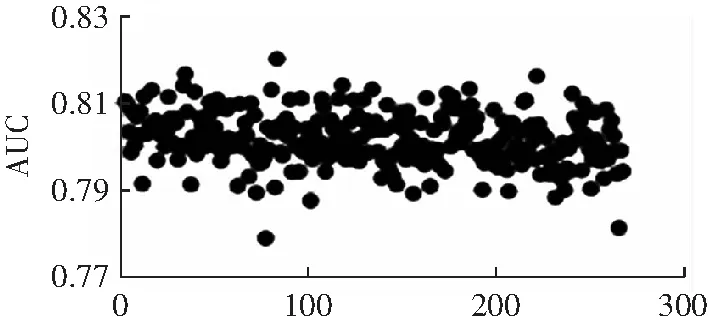
聚类簇数图7 不同聚类簇数下的AUC值

为了避免偶然性对实验结果的影响，对各个算法重复进行10次5折交叉验证并取平均值作为最终的实验结果。实验结果如表3和表4所示，每个数据集对应的评价指标的最优值用黑体标出。

表3 各算法与KNN分类器结合时的分类表现

表4 各算法与Random Forest分类器结合时的分类表现

通过比较各个算法的F1、G-mean、AUC值发现，在五组数据的分类度量指标的平均值上，当使用KNN分类器时，FCMUSIC算法的F1值平均提高了6.65%，G-mean值平均提高了7.75%，AUC值平均提高了1.96%；RUS算法在对应指标上分别提高了6.21%、7.37%和1.94%；CBUS1算法分别提高了 5%、6.37%和0.69%。在这些算法中，FCMUSIC算法的提升幅度最大，这也证明了FUCMSIC算法的有效性。 具体表现在对于pima、yeast1、haberman和german四个数据集，FCMUSIC算法和RUS算法、CBUS1算法的整体性能都比原始不平衡数据集有明显提高，而在segment0数据集上， FCMUSIC算法和其他的欠采样算法都比直接在初始的不平衡数据集上训练分类器的总体表现要差，特别是F1值有较大的下降，分析下降的原因，与样本的分布有关，segment0数据集的多数类和少数类样本的空间分布具有明显的区别，传统的分类器可以直接在不平衡数据集上找到精准的分类超平面，由于segment0数据集的不平衡比率较大，欠采样的方法会不可避免地丢失多数类的部分信息，使得分类性能有所下降。但FCMUSIC算法比其他算法下降的幅度要小。这也表明FCMUSIC算法具有一定的稳定性。

当各个算法与RF分类器结合时，FCMUSIC算法在各个数据集上的F1值平均提高了5.31%，G-mean值平均提高了6.07%，AUC值则平均下降了0.59%，RUS算法在F1和G-mean值上分别提高了5.14%和5.88%，AUC下降了0.55%，CBUS1算法在F1和G-mean值上分别提高了2.95%，2.62%，AUC下降了3.17%。欠采样算法比原始数据集建模的AUC值有所下降，但整体分类性能仍然有不同程度的提高。在各个数据集上，FCMUSIC算法的G-mean值比CBUS1算法要高。 FCMUSIC算法的分类结果也表明了该算法具有良好的分类性能。

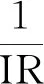
根据实验结果可以看出，FCMUSIC算法与KNN和RF分类器结合，都提高了分类器的分类性能，表明FCMUSIC算法具有一定的独立性，不依赖于特定的分类器。就分类器而言，与KNN分类器结合时的提升幅度更大，与RF分类器结合时的分类表现更好。就评价指标而言，在F1和G-mean值上的提升幅度更大。

4 结语

针对传统分类器在不平衡数据集上分类性能降低的情况，本文结合聚类算法，提出了基于FCM的簇内欠采样算法——FCMUSIC。FCMUSIC算法能够有效提升分类器的分类性能，特别是F1值和G-mean值。通过与不同的分类器结合，验证了FCMUSIC算法的独立性，与其它欠采样算法进行对比，验证了FCMUSIC算法的有效性，表明FCMUSIC算法能够作为一种有效的欠采样算法，用来提高分类器对不平衡数据集的分类性能。