Fermat型偏微差分方程解的存在性及形式

汪 楠，徐洪焱，刘 林

(1.江西医学高等专科学校医学影像系，江西 上饶 334001;2.上饶师范学院数学与计算机科学学院，江西 上饶 334001)

1 引言及主要结果

文章假定读者熟悉Nevanlinna值分布理论，我们将采用Nevanlinna理论的基本符号[1-3]。随着Nevanlinna理论在差分领域的快速发展，许多学者在差分方程等方面获得了一系列重要且有趣的结果(见文献[4-9])。2012年间，刘凯，杨连中等[7-9]讨论了几类Fermat型复域微分、差分方程

f′(z)2+f(z+c)2=1

(1.1)

f(z)2+f(z+c)2=1

(1.2)

f(z)2+f′(z)2=1

(1.3)

其中c∈为非零常数，他们得到:方程(1.1)的有限级超越整函数解必为f(z)=sin(z±Bi)，其中c=2kπ或c=(2k+1)π，B∈，k∈N；方程(1.2)的有限级超越整函数解必为f(z)=sin(Az+B)，其中，k∈N；方程(1.3)的有限级超越整函数解为f(z)=sin(z+c)，c∈。

2018年，Xu-Cao[10-11]利用多复变Nevanlinna值分布理论以及差分模拟结果，讨论了多变量Fermat型偏微-差分方程解的性质，将刘凯等人的结果推广到多变量情形。

定理A[10-11]设c=(c1，c2)∈2，则偏微差分方程

的任意有限级超越整函数解具有形式f(z1，z2)=sin(A1z1+A2z2+B)，其中A1，A2，B为常数，满足A1eiA1c1=1，特别地，若c1=0，则f(z1，z2)=sin(z1+A2z2+B)。

定理B[10]设c∈n{0}。那么Fermat型偏微差分方程

f(z)2+f(z+c)2=1

(1.4)

的解具有

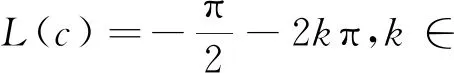
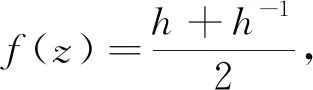
由于涉及多变量差分Nevanlinna理论[12-13]起步较晚，有关复域偏微分与差分方程的文献并不多，关于Fermat型偏微差分方程的还有许多问题有待研究。本文将针对此问题，进一步讨论Fermat型偏微差分方程解的存在性条件及其形式，获得结果如下：

定理1.1设c=(c1，c2)∈2-{(0，0)}，若f(z1，z2)为方程

(1.5)

的有限级超越整函数解，则f(z1，z2)具有形如

这里L(z)=μ1z1+μ2z2;a1，a2≠0且L(c)=μ1c1+μ2c2，μ1，μ2，b∈满足以下情况之一:

以下例子显示方程(1.5)解的存在性。

例1.1若

则f(z1，z2)为方程(1.5)的有限级超越整函数解，其中μ1=0，μ2=2，b∈，。

例1.2若

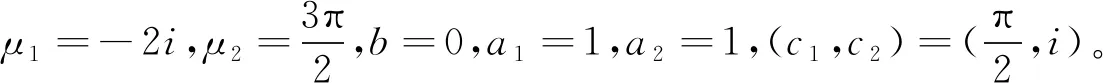
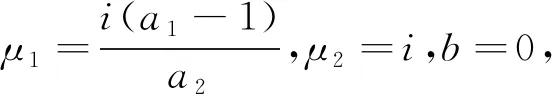
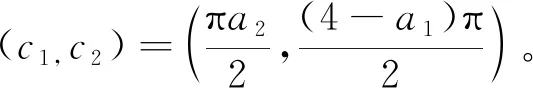
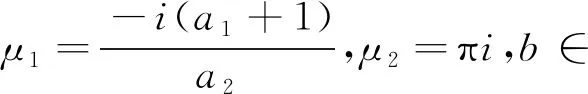
则易知f(z1，z2)为方程(1.5)的有限级超越整函数解。

若方程(1.5)同时包含两类偏微分以及差分，那么

定理1.2设c=(c1，c2)∈2{(0，0)}，s=c2z1-c1z2。若f(z1，z2)为方程

(1.6)

的有限级超越整函数解，则f(z1，z2)具有

这里a1≠0，a2，a3不同时为零，L(z)=μ1z1+μ2z2，H(s)是关于s的多项式且L(c)=μ1c1+μ2c2，μ1，μ2，b∈满足以下情况之一:

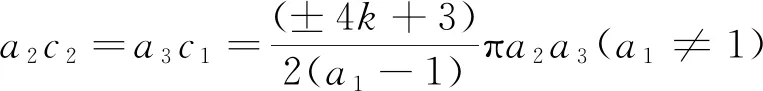
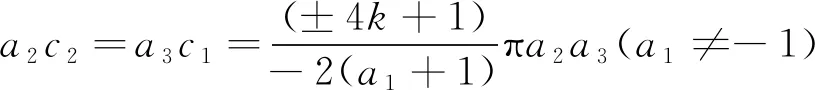
(ⅱ) 若a2c2≠a3c1，则H(s)≡0且

或

下列例子说明方程(1.6)解的存在性与形式的准确性。

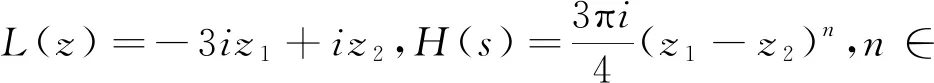
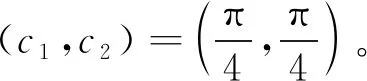
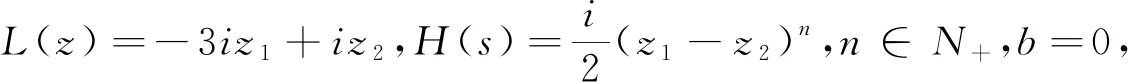
例1.7令L(z)=iz1-iz2，H(s)≡0，b=0，则

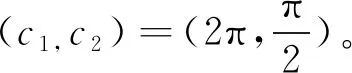
例1.8令L(z)=-iz1-iz2，H(s)≡0，b=0，a1=1，a2=a3=1，则

2 引理

文章须用到以下引理。

引理2.1[14-15]若F为n上的整函数，F(0)≠0，ρ(nF)=ρ<∞，则存在函数fF与gF∈n，满足F(z)=fF(z)egF(z)，特别地，当n=1时，fF是魏尔斯特拉斯函数。

注2.1这里ρ(nF)是零点计数F的阶数。

引理2.2[3]若g与h是复平面的整函数，且g(h)是有限级整函数，则存在以下两种情况：

(ⅰ)h为多项式，g为有限级整函数；

(ⅱ)h为非多项式的有限级整函数，g为零级超越整函数。

引理2.3[16]设fj(≠0)，j=1，2，3是m上的亚纯函数，f1非常数。如果f1+f2+f3=1以及

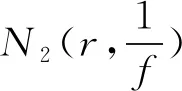
3 定理1.1的证明

设f(z)为方程(1.5)的有限级超越整函数解，重写方程(1.5)为

(3.1)

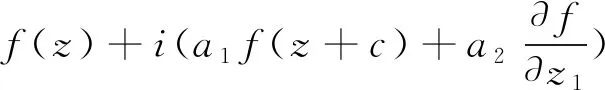
于是

(3.2)

(3.3)

将(3.2)代入(3.3)，得

(3.4)

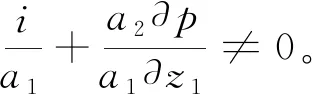
(3.5)

由(3.4)，(3.5)，得

(3.6)

根据(3.5)，(3.6)，可知e2[p(z+c)-p(z)]=-1，可得

p(z)=L(z)+H(s)+b，e2L(c)=-1

这里L是一个线性函数，形如L(z)=μ1z1+μ2z2，H(s)是关于s的多项式，其中s=c2z1-c1z2，μ1，μ2，b∈。

另一方面，由(3.5)，(3.6)知

即

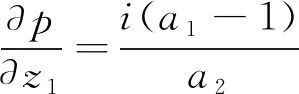
由(3.5)或(3.6)，知

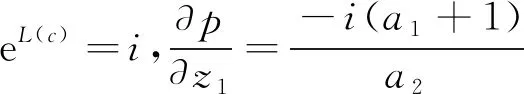
那么

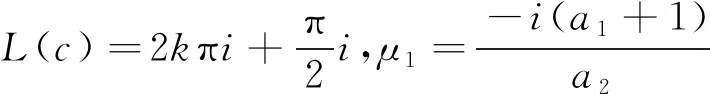
如果c2=0，即H(s)=H(-c1z2)，又因为e2[p(z+c)-p(z)]=-1，则degsH≤1。

如果c2≠0，易知H(s)是关于s的多项式且degsH≤1。因此，L(z)+H(s)+b是关于z1，z2的线性，不妨设μ1z1+μ2z2+b，μ1，μ2，b∈。结合(3.5)与(3.6)，则

这里L(z)=μ1z1+μ2z2，且L(c)，μ1，μ2，b∈满足

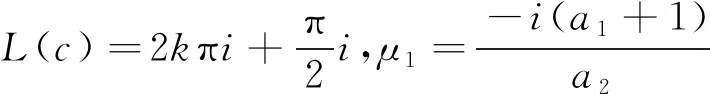
于是，定理1.1得证。

4 定理1.2的证明

假设f(z)是方程(1.6)的解，类似上述证明，存在非常数多项式p(z)，使得

(4.1)

(4.2)

由(4.1)与(4.2)得

e2[p(z+c)-p(z)]=-1

于是p(z)=L(z)+H(s)+b，这里L是线性函数，形如L(z)=μ1z1+μ2z2，H(s)是关于s的多项式，其中s=c2z1-c1z2，μ1，μ2，b∈，且e2L(c)=-1。

另一方面，由(4.1)，(4.2)得

再根据上述所知p(z)=L(z)+H(s)+b，有

(4.3)

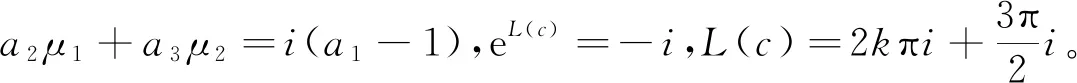
若a1=1，a2μ1+a3μ2=0，则L(c)=0，eL(c)=1，这与上述e2L(c)=-1矛盾。

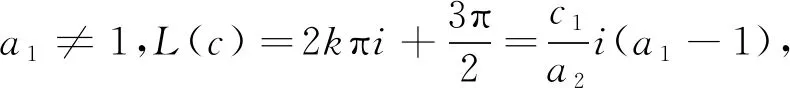
这里k∈Z。

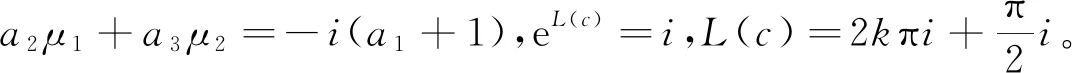
若a1=-1，a2μ1+a3μ2=0，则L(c)=0，eL(c)=1，这与上述e2L(c)=-1矛盾。

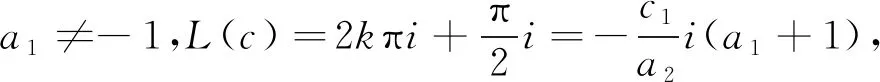
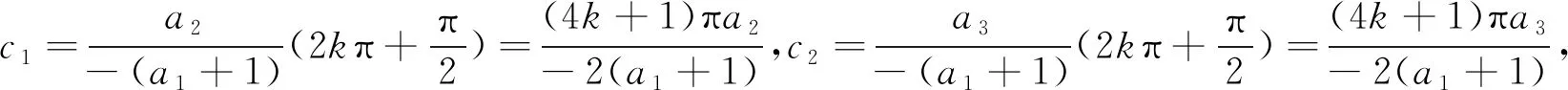
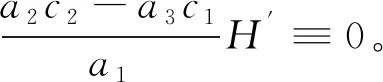
或

综上，定理1.2证毕。