高维多项式理想的实根计算

杨雪英，肖水晶

(南昌大学理学院，江西 南昌 330031)

在实代数几何中，多项式理想的实根扮演着如同根理想在复代数几何中一样的角色。与多项式理想的根的计算相比较，计算多项式理想的实根要困难得多。近年来，研究零维多项式理想的实根计算文献较多，但对高维多项式理想的实根计算问题的研究相对较少。一般说来，研究者主要从数值计算和符号计算两方面来研究多项式理想的实根计算问题。

在符号计算方面，Beker和Neuhaus在文献[1-2]中通过Gröbner基[3-4]给出一个计算零维理想实根的算法。由于Gröbner基的计算本身就存在比较大的难度，所以该算法实现起来比较复杂。1998年，Neuhaus在文献[2]中对该算法进行了修改与整理，并给出了高维多项式理想实根的计算算法，最后还给出了实根理想生成元的次数上界为D2O(n2)，其中D是输入多项式次数上界，n为变元个数。该算法在研究实代数簇的孤立点性质的基础上，将高维多元多项式理想转化为零维理想，再通过Shape-Lemma[5-6]转化为单个多项式情形。对于单个多项式情形，则通过准素分解将多项式转化为不可约多项式情形。对于一个不可约多项式P∈K[x1,x2,…,xn]，由变号准则[2]判断不可约多项式P是否为实，从而得出计算多项式理想实根的算法。Spang在文献[7-8]中通过研究极大理想的性质从而避免了[1-2]中算法产生的一些坐标变换，提高了运算效率并给出计算零维理想实根的算法。在文献[9-10]中，Yang和Zhi从代数簇光滑情形与一般情形出发给出了计算多项式理想实根的所有极小素理想的生成元的概率算法，算法的复杂为So(1)(nD)O(nr2r)，其中D是多项式次数上界，n为变元个数，r为生成理想的多项式个数。进一步，Yang和Zhi在文献[11]中提出了多项式环中S-根的概念，并给出计算S-根的所有极小素理想生成元的概率算法。

在数值计算方面，Lasserre等在文献[12]中基于半正定规划(SDP)松弛的性质，给出了计算零维多项式理想实根以及S-根的算法。该算法很好地利用了半正定规划以及数值线性代数的性质，在不需要计算复零点的情况下可计算出所有的实零点。Lasserre等人在文献[13]中介绍了一种新算法，在边界基算法[14]中引入矩量矩阵(moment matrics)的半正定性限制，相对于文献[12]中半正定规划松弛更容易处理。马玥等在文献中基于矩量矩阵去计算Pommart基[16]，在文献[12-13]中算法的基础上推广到高维多项式理想情形。Brake等人在文献[17]中基于数值代数几何与平方和规划，给出了一个计算实根理想生成元的算法。

本文从符号计算的角度出发，考虑如何有效地计算K[x1,x2,…,xn]中高维多项式理想I的实根。与文献[2]一样，本文先考虑零维理想的情形，再通过多项式环的典范同态映射:

K[x1，…，xn]→K(x1，…，xs)[xs+1，…，xn]

将高维理想扩张为零维理想，从而建立计算高维多项式理想实根的方法。

1 预备知识

定义1.1(理想的根与根理想)设I为多项式环K[x1，x2，…，xn]中一个理想，I的根定义为

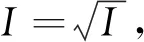
下面为代数几何学中著名的Hilbert零点定理，该定理揭示了代数簇与根理想之间的对应关系。

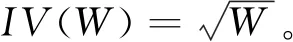
设I是K[x1，x2，…，xn]中一个理想，若存在一个有限多项式集合{g1，g2，…，gs}使得I=〈g1,g2,…,gs〉，即称I由{g1,g2,…,gs}生成。

引理1.3[19]设I1，I2是多项式环K[x1，x2，…，xn]中任意两个理想，则以下结论成立:

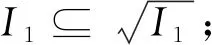
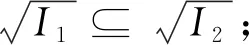
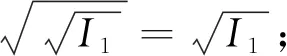
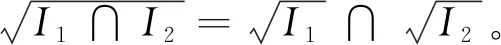
定义1.4([1]，Definition2.1或[19]，85页)(多项式理想的实根)设K是一个实域，I⊆K[x1，x2，…，xn]是一个多项式理想，I的实根定义为

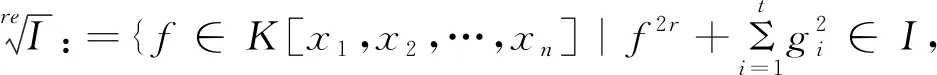
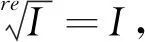
同样地，在实代数几何中有著名的实零点定理，证明详见文献[2]。

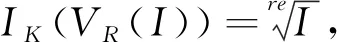
根据以上定义和定理我们可以得出如下引理

引理1.6([7]，Lemma1.8)设I，I1，I2是K[x1，x2，…，xn]中理想，则以下结论成立:

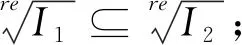
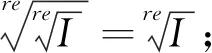
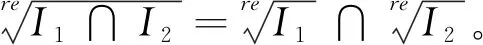
2 零维多项式理想的实根计算

2.1 单变量情形

本节讨论单变量多项式环K[x]中理想实根的计算。由于K[x]是一个主理想环，从而首先确定不可约多项式能否生成一个实理想。

定理2.1.1设q是K[x]中不可约多项式，则q生成的理想〈q〉是实的，当且仅当q在K的实闭包中有一个根。

证明记R为K的实闭包。设理想〈q〉是实的，则K[x]/〈q〉是一个实环。由于q是K[x]中不可约多项式，从而K[x]/〈q〉是K的一个有限(代数)扩张。由实闭包的唯一性知，K[x]/〈q〉是R的一个子域。这样，q在实闭包R中有一个根x+〈q〉。

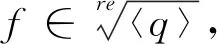
根据定理2.1.1，对于g∈K[x]，我们可按如下步骤计算〈g〉的实根。

算法2.1.2(计算K[x]中理想的实根)

输入：一个多项式g∈K[x]。

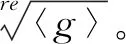
计算过程：

步骤1将多项式g进行如下唯一分解：

其中pi(i=1，2，…，r)为K[x]中不可约多项式，ε∈K{0}，m1，m2，…，mr∈N。

步骤2抽出次数为奇数的不可约多项式，组成一个集合T1。

步骤3对于次数为偶数的不可约多项式，依次通过Sturm定理判断出多项式是否存在实根。抽出次数为偶数且有实根的不可约多项式组成一个集合T2。

步骤4输出结论：

这里T=T1∪T2。

2.2 单个多项式情形

本节主要讨论单个多项式情形。以下引理为单个多元多项式所生成的主理想是否为实提供了重要的判定方法。

引理2.2.1([7]，Lemma3.1或[1]，Lemma4.1)设多项式P∈K[x1，x2，…，xm，x]，其中P是一个次数大于零的不可约多项式，则下列命题是等价的:

(1) 〈P〉·K(x1，x2，…，xm)[x]是实的。

(2) 〈P〉·K[x1，x2，…，xm，x]是实的。

(3)P是不定的，即存在实数a，b∈Rm+1满足P(a)·P(b)<0。

文献[20，21]中给出了判定一个多项式是否不定的算法。由引理2.2.1，可以得出如下算法。

算法2.2.2(计算K(x1，x2，…，xm)[x]中主理想的实根)

结构：K是一个完满域，且对于任意一个变元集形成的域都是完满域。

输入：一个多项式f∈K(x1，x2，…，xm)[x]。

计算过程:

步骤1在K(x1，x2，…，xm)[x]中，将多项式f进行如下唯一分解：

其中pi(i=1，2，…，r)为K(x1，x2，…，xm)[x]中不可约多项式，ε∈K{0}，m1，m2，…，mr∈N。

步骤2对于每个不可约多项式pi，判断其不定性。抽出所有不定的不可约多项式组成一个集合T。

步骤3输出结论：

2.3 多元多项式情形

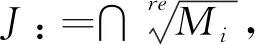
·primdecGTZ，primdecSY.输入K[x1，x2，…xn]中理想I=〈f1，f2，…，fs〉，输出I的素分解理想。

由文献[7]中Remark 4.16以及引理1.6(4)得零维理想实根的计算算法RealZero(参见Singular程序包realrad)，具体如下:

算法2.3.1(零维多项式理想的实根计算)

结构:K是一个完满域，且对于任意一个变元集形成的域都是完满域。

输入：K[x1，x2，…xn]中零维多项式理想I，I=〈f1，f2，…，fs〉。

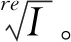
计算过程:

步骤1根据文献[7]中Remark 4.16，将I=〈f1，f2，…，fs〉简化为:

J=〈g1，g2，…，gs〉

步骤2调用算法primdecGTZ或primdecSY(取决于哪个算法更快)将J进行素分解得到极大理想M1，M2，…，Ms，令Max:={M1，M2，…，Ms}。

步骤3若Max≠∅，则选择一个Mi∈Max，令Max:=Max{Mi}。

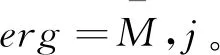
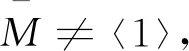
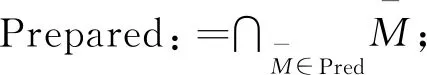
NonPrepared:=GeneralPos(NonPrep)。

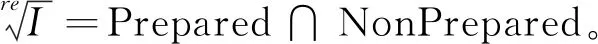
3 高维多项式理想的实根计算

3.1 理想的扩张与收缩

设K[x1，x2，…，xn]和K(x1，x2，…，xs)[xs+1，xs+2，…，xn]是带有单位的可交换多项式环，I是K[x1，x2，…，xn]中一个理想，{x1，x2，…，xs}表示I在K[x1，x2，…，xn]中的一个极大无关变元组。定义一个多项式环的典范同态映射:

在该环典范同态映射中，若有a∈K(x1，x2，…，xs)[xs+1，xs+2，…，xn]，s∈K[x1，x2，…，xs]，则sa∈K[x1，x2，…，xn]。

若不加说明，本章所涉及的多项式环的典范同态映射都为Φ。以下给出该映射中理想的扩张与收缩的定义，该定义是文献[22]中一般代数几何所定义的扩张理想与收缩理想在多项式代数中的特殊化。

定义3.1.1在多项式环的典范同态映射Φ中，设I1是K[x1，x2，…，xn]中一个理想，则把I1的同态像Φ(I1)在K(x1，x2，…，xs)[xs+1，xs+2，…，xn]中生成的理想称作I1在Φ上的扩张理想，记作Ie;设I2是K(x1，x2，…，xs)[xs+1，xs+2，…，xn]中理想，易证Φ-1(I2)为K[x1，x2，…，xn]中理想，此时称Φ-1(I2)为I2在Φ上的收缩理想，记作Ic。

根据理想的扩张与收缩的定义，可以得出以下性质，并给出简要的证明。

引理3.1.2在多项式环的典范同态映射Φ中，设I，I1，I2为K[x1，x2，…，xn]中理想，J，J1，J2为K(x1，x2，…，xs)[xs+1，xs+2，…，xn]中理想，则下列结论成立:

(1) (I1+I2)e=(I1)e+(I2)e;

(2) (J1+J2)c⊇(J2)c+(J2)c;

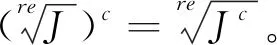
证明(1) 由多项式理想扩张的定义知，

其中fi1，fi2∈I1，gi∈K(x1，x2，…，xs)[xs+1，xs+2，…，xn]，fi1，fi2，gi为多项式，i为有限的。

(2) 由理想收缩的定义知，(J1+J2)c=Φ-1(J1+J2)，从而

(J2)c+(J2)c=Φ-1(J1)+Φ-1(J2)。

再由同态映射性质得，(J2)c+(J2)c⊆(J1+J2)c。

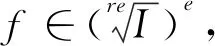
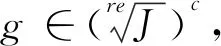
3.2 高维向零维的扩张

由文献[23]引理9.3.6知，在多项式环的典范同态中可以通过理想的扩张将高维理想转化为零维理想。

定理3.1.1([22]，Lemma8.13)设I是K[x1，x2，…，xn]中的一个真理想，U={x1，x2，…，xs}是I的一个极大无关变元组，则I关于同态映射Φ的扩张理想Ie在环K(x1，x2，…，xs)[xs+1，xs+2，…，xn]中是零维理想。

3.3 高维理想的实根计算

接下来我们讨论将计算出的实根如何收缩回原来的多项式环中，即可计算出高维多项式理想的实根。为此，先引入以下命题。

命题3.3.1设I=〈f1，f2，…，ft〉是K[x1，x2，…，xn]中一个理想，则存在正整数k使得

I=〈I，Lk〉∩〈I:Lk〉

其中G是I的一个Gröbner基，L=lcm{hc(g)|g∈G}，hc(g)∈K[x1，x2，…，xs]是多项式g在环K(x1，x2，…，xs)[xs+1，xs+2，…，xn]中的首项系数。

证明由理想的饱和定义知，存在正整数k使得I:Lk=I:L∞，由文献[24]中算法22可计算得到k。显然I⊆〈I，Lk〉∩(I:Lk)。

接下来证明〈I，Lk〉∩(I:Lk)⊆I。设f∈〈I，Lk〉∩(I:Lk)，则fLk∈I，且存在g∈I与h∈K[x1，x2，…，xn]使得f=g+Lkh，两边同乘Lk得Lkf=Lkg+L2kh。从而有L2kh=Lkf-Lkg∈I，于是h∈I:L2k。由于I:L2k⊆I:L∞=I:Lk，从而h∈I:Lk，于是Lkh∈I。又因为g∈I，所以f=g+Lkh∈I。

综上，存在正整数k使得I=〈I，Lk〉∩(I:Lk)成立。

由命题3.3.1及[24]中命题3.2.30，可以得出以下推论。

推论3.3.2设I是K[x1，x2，…，xn]中一个理想，G为I的一个Gröbner基，则存在正整数k使得

I=〈I，Lk〉∩Iec

其中L=lcm{hc(g)|g∈G}，且hc(g)∈K[x1，x2，…，xs]是g在环K(x1，x2，…，xs)[xs+1，xs+2，…，xn]中的首项系数。

证明由[24]中命题3.2.30知，当I0=Ie时，存在正整数k使得Iec=I:L∞=I:Lk成立。由命题3.3.1知，此时k使得I=〈I，Lk〉∩(I:Lk)成立，于是I=〈I，Lk〉∩Iec。

基于推论3.3.2，我们可以建立如下算法。

算法3.3.3(计算L及正整数k使得I=〈I，Lk〉∩Iec)

结构：K是一个完满域，且对于任意一个变元集形成的域都是完满域。

输入：I⊆K[x1，x2，…，xn]。

输出：L∈K[x1，x2，…，xs]，及正整数k使得I=〈I，Lk〉∩Iec。

计算过程:

步骤1计算I在K[x1，x2，…，xn]中的Gröbner基G=(g1，g2，…，gm)(1≤m≤n)。

步骤1.1对任意的gi∈G，计算出gi在K(x1，x2，…，xs)[xs+1，xs+2，…，xn]中的首项系数hc(gi)。

步骤1.2对于上述所有的首项系数，在K(x1，x2，…，xs)[xs+1，xs+2，…，xn]中计算出最小公倍数，记作L=lcm{hc(gi)|gi∈G}。

步骤2由理想饱和的定义或文献[24]中算法22计算出k。

步骤3输出L∈K[x1，x2，…，xs]，及正整数k使得I=〈I，Lk〉∩Iec。

证明由Gröbner基的有限性知算法具有终止性，正确性由推论3.3.2直接得出。

由推论3.3.2及多项式理想实根的相关性质，则得出以下定理成立，该定理为本文算法3.3.5中主要思想。

设{f1，f2，…，ft}∈K[x1，x2，…，xn](1≤t≤n)，I=〈f1，f2，…，ft〉，U={x1，x2，…，xs}是I的一个极大无关变元组，且R表示Ie在K(x1，x2，…，xs)[xs+1，xs+2，…，xn]上的实根。由文献[24]中算法23计算出R在K[x1，x2，…，xn]上的收缩理想的基Λ，根据推论3.3.2，由算法3.3.3计算出非零元L以及正整数k使得

I=〈f1，f2，…，ft〉=〈{f1，f2，…，ft}∪{Lk}〉∩〈f1，f2，…，ft〉ec

定理3.3.4设记号同上描述，则I=〈f1，f2，…，ft〉的实根等于所有〈{f1，f2，…，ft}∪{Lk}〉的实根与〈Λ〉的交集，即

证明若1∈I正确性显然;若1∉I，由推论3.3.2知L，k满足

〈f1，f2，…，ft〉=〈{f1，f2，…，ft}∪{Lk}〉∩〈f1，f2，…，ft〉ec

则两边分别求实根得

由以上定理可以得出以下算法。

算法3.3.5(高维多项式理想的实根计算)

结构：K是一个完满域，且对于任意一个变元集形成的域都是完满域。

输入：{f1，f2，…，ft}∈K[x1，x2，…，xn]是I的生成元，即I=〈f1，f2，…，ft〉。

输出：I的实根的基ξ。

计算过程：

步骤1如果1∈{f1，f2，…，ft}，那么显然ξ等于1;若1∉{f1，f2，…，ft}，则根据[23]中引理9.3.6中计算极大无关变元组的讨论计算出I的一个极大无关变元组U={x1，x2，…，xs}。

步骤2调用算法2.3.1，计算出Ie在K(x1，x2，…，xs)[xs+1，xs+2，…，xn]中的实根R。

步骤3文献[24]中算法23(取决于哪种方法更快)计算出R在K[x1，x2，…，xn]上的收缩理想的基Λ。

步骤4调用算法3.3.3计算出非零元L以及正整数k使得

I=〈f1，f2，…，ft〉=〈{f1，f2，…，ft}∪{Lk}〉∩〈{f1，f2，…，ft}〉ec

步骤5计算〈{f1，f2，…，ft}∪{L}〉的实根的基，再把实根的基与〈Λ〉作交集，得出的交集即为I的实根的基ξ。

证明终止性:若1∈{f1，f2，…，ft}，终止性显然;

若1∉{f1，f2，…，ft}，根据U是极大无关变元组，则〈f1，f2，…，ft〉∩K[U]={0}则L∉I，即〈f1，f2，…，ft〉⊂〈{f1，f2，…，ft}∪{L}〉。

以上步骤是对多项式理想的实根计算进行递归调用，且输入的有限多项式集生成的理想构成严格升链，由有限升链条件即得终止性。

正确性:由定理3.3.4可得出。

复杂度分析:记degfi(1≤i≤t)为输入多项式组{f1，f2，…，ft}中多项式次数，m为输入多项式组变元个数，s为极大变元个数。算法3.3.5的第1步计算I的一个极大无关变元组，可实现这一步骤的方法参见[23]中引理9.3.6，由[23]中引理9.3.6中极大无关变元组的讨论，可知第1步的复杂度为O(s2)(0≤s≤n)。

接下来，由文献[7]中算法RealZero，计算零维理想在多项式环中的实根的复杂度为Max(deg(fi))2O(m2)。步骤3中计算实根理想的收缩，由[24]中命题3.2.30知，计算收缩理想的复杂度是计算多项式集的Gröbner基所产生。由计算Gröbner基的算法Buchberger知，由[24]中定理2.3.22知对多项式集进行循环运算直至计算出Gröbner基G，因此步骤三的复杂度为O(nt2)。

步骤4中调用算法3.3.3计算出非零元L以及正整数k使得

I=〈f1，f2，…，ft〉=〈{f1，f2，…，ft}∪{Lk}〉∩〈{f1，f2，…，ft}〉ec

由算法3.3.3计算步骤1与步骤2，知算法3.3.5步骤四的复杂度不会超过Max(deg(fi))2O(m2)。因为该算法中关键步骤的复杂度都不超过Max(deg(fi))2O(m2)，所以该算法的整体复杂度为Max(deg(fi))2O(m2)。