Winkler地基上矩形薄板的振动响应分析
2021-12-15郑双星高芳清丁凯文
郑双星,高芳清,2,丁凯文
(1.西南交通大学 力学与工程学院,成都 610031;2.西南交通大学 应用力学与结构安全四川省重点实验室,成都 610031)
分析弹性地基上矩形薄板振动响应问题可以采用能量变分法[1-2]、有限元法[3-6]、样条元法[7-10]。另外,颜可珍[11]通过级数展开法和Laplace-Fourier 变换方法得到了薄板在半波正弦冲击荷载作用下位移和应力的解析解。袁松等[12]运用接触力学的理论对Winkler地基模型落石冲击力计算方法进行了研究。吴波[13]用曲厚板单元分析法对弹性地基上不规则厚板的简载应力进行了求解。
对于地基上板类结构常采用Winkler地基建模,该模型形式简单、参数设定简洁,为工程界普遍接受而得到广泛应用。本文通过Winkler 地基模型反映地基-薄板结构相互作用关系,通过弹性组件的设定来模拟矩形薄板边界约束类别[14],采用Li 等[15-16]提出的改进的傅里叶级数方法来表示横向位移,通过数值计算,求得Winkler地基上矩形薄板的振动响应曲线,并通过和有限元结果进行对比,表明本文方法精度较高。此外,该方法收敛速度也比较快。
1 理论模型
1.1 改进傅里叶级数解
对于弹性约束边界条件下单一矩形板结构来说,其横向位移函数可以采用二维改进傅里叶级数形式表示,即在标准二维傅里叶余弦级数基础上增加辅助函数与单傅里叶余弦级数的乘积[17-18];通过辅助函数的引入,可以解决传统的傅里叶级数的导数在边界处潜在的不连续性问题,同时还可以改善级数的收敛性。
横向位移函数用二维改进傅里叶级形式表示为
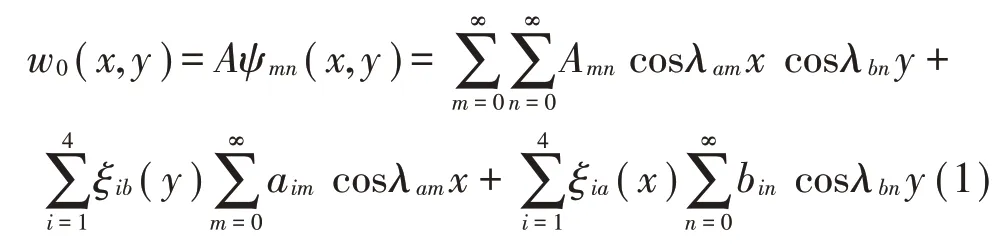
式中:A和aim、bin分别为横向位移函数w0(x,y)中二维傅里叶级数和辅助级数的未知系数向量,λam=mπ/a,λbn=nπ/b,向量A、ψmn(x,y)的形式以及x相关的辅助函数ξia(x)可表示为:

将式(4)至式(7)中a和x分别替换为b和y即可得到辅助函数ξib(y)的表达式。
1.2 计算模型建立
计算模型如图1所示。基于Winkler地基模型,在垂直于x-y平面方向采用均匀分布的竖向弹簧模拟地基作用,该竖向弹簧相互独立且互不影响;采用系列横向弹簧和扭转弹簧组件来模拟矩形薄板边界(kx0、kxa和Kx0、Kxa分别为x=0和x=a边界上的横向弹簧刚度和扭转弹簧刚度,ky0、kyb和Ky0、Kyb分别为y=0和y=b边界上的横向弹簧刚度和扭转弹簧刚度);f(x,y,t)为施加于薄板上(x0,y0)位置处的简谐横向集中力。
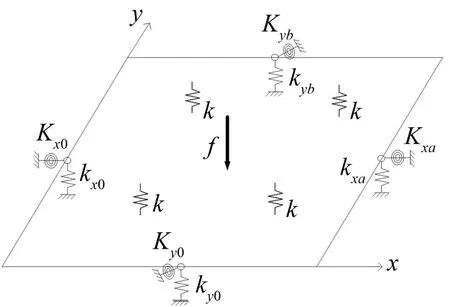
图1 受简谐横向集中力作用Winkler地基上矩形薄板模型
具有弹性边约束和结构阻尼的板振动控制微分方程式为:
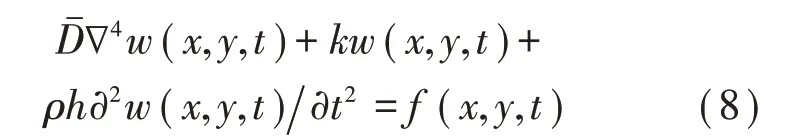
简谐横向集中力(幅值为)可表示为:
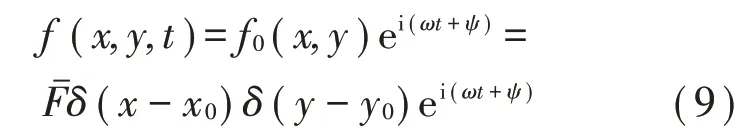
此时,横向位移可以写为:
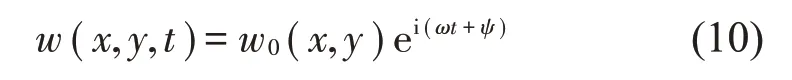
将式(9)、式(10)代入式(8),可以得到:
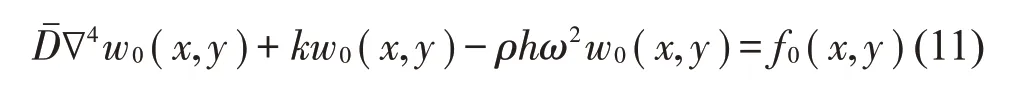
本文采用能量法求解振动方程式(11)。
在外部荷载作用下Winkler 地基上矩形板结构拉格朗日函数表示为:
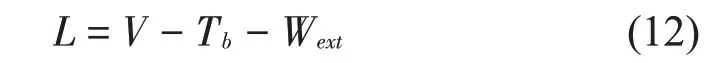
式中:V为Winkler地基上矩形薄板的总势能,Tb为该结构的总动能,Wext为外力的势能的负值。
系统中存储的总势能V可表示为:

式中:Vf为Winkler 地基的变形势能,Vb为弯曲应变能,Vs为边界弹簧的弹性势能,其具体表达式可以参见文献[19]。
Wex可以表示为:
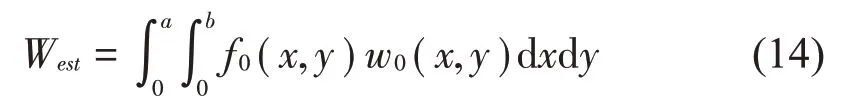
将式(1)代入拉格朗日函数式(11)中,然后用瑞利-里兹方法对该拉格朗日函数求极值,可以得到一个线性方程组,将其用矩阵表达式表示为:

式中:K、M分别为Winkler 地基上矩形薄板系统的刚度矩阵和质量矩阵,其取值只与系统的结构特征地基参数和边界条件有关。
F为横向集中力作用向量,即:

任意激励频率ω下矩形板结构振动响应的傅里叶系数向量A可由式(15)直接得到:
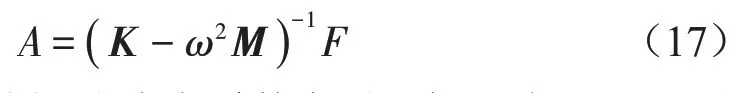
将求得的振动响应系数向量A代入式(1),再通过式(10)即可得到该激励下矩形薄板结构在任意时刻的横向位移。
对于简谐振动,在计算出结构振动位移响应之后,结构振动速度可以由v=jωw直接获得,根据得到结果的实部与虚部,即可求得速度的幅值与相位。
向量F取为零向量,即可进行模态分析,求得固有频率。
2 数值计算与分析
给定如下参数:板长a=1.0 m,宽b=1.0 m,厚h=0.008 m,密度ρ=7 800 kg/m3,弹性模量E=2×1011N/m2,泊松比μ=0.3,地基基床系数k=5.5×107N/m3,阻尼系数η=0.02。为表述简洁,下文中用F表示自由边界条件(横向弹簧刚度设置为0,扭转弹簧刚度系数设置为0),S表示简支边界条件(横向弹簧刚度设置为1010N/m,扭转弹簧刚度系数设置为0),C表示固支边界条件(横向弹簧刚度设置为1010N/m,扭转弹簧刚度系数设置为1010N∙m/rad)。ANSYS 有限元模型中采用shell63 单元,网格划分尺寸为0.01 m×0.01 m。
表1 给出了截断值M、N取值为6 时Winkler 地基上不同边界条件下矩形薄板前6阶固有频率与有限元结果对比。从表中可以看出,无论取何种边界条件,两种方法所求出的固有频率都非常接近。
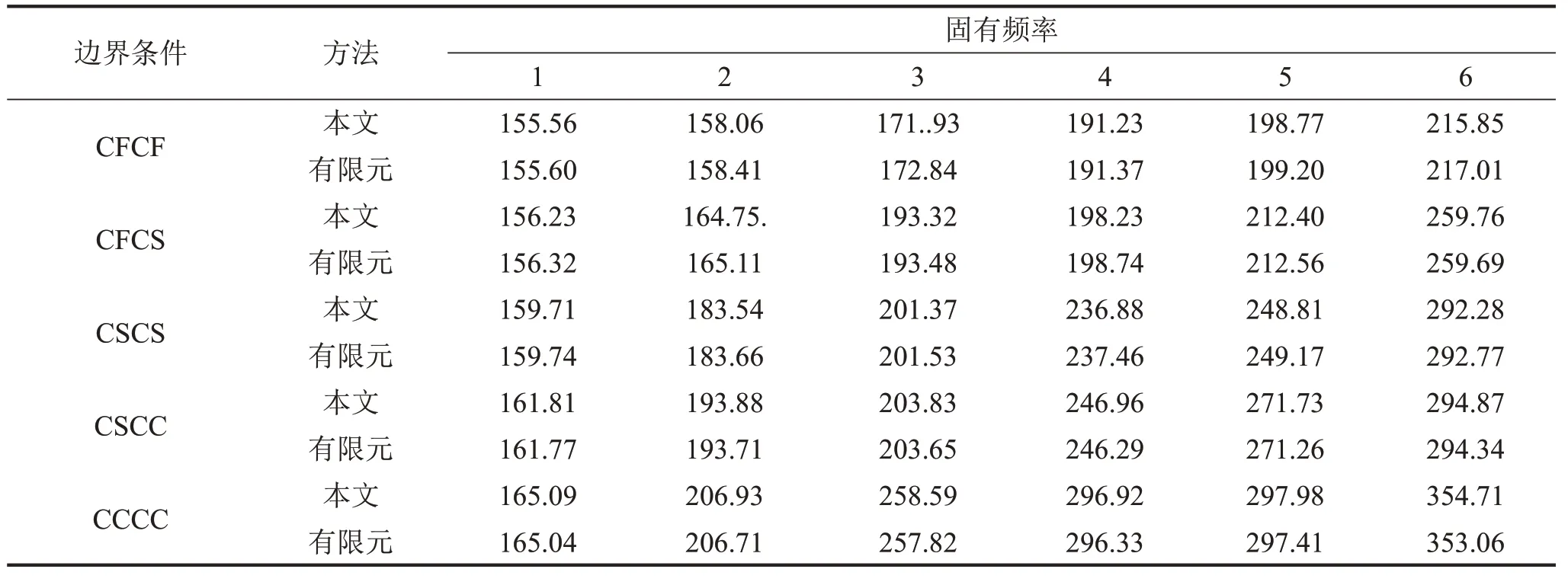
表1 Winkler地基上不同边界矩形薄板的固有频率/Hz
在以下分析中,所有边界条件均取为简支。
表2给出了四边简支条件下基于本文方法及有限元法所得500 Hz以下的固有频率。

表2 Winkler地基上四边简支矩形薄板的固有频率/Hz
将幅值为1 N的简谐横向集中力施加于板中心位置(0.5 m,0.5 m),并在0~500 Hz 频率范围内进行正弦扫描,同时对该作用点和(0.8 m,0.8 m)位置处的振动速度幅值进行观测。此外,为了验证本文方法的可靠性,采用ANSYS有限元方法对相同问题进行了计算,并与程序计算结果进行对比,如图2所示。
将幅值为1 N 的简谐横向集中力施加于板(0.8 m,0.8 m)位置处,并在0~500 Hz 频率范围内进行正弦扫描,同时对该作用点和(0.5 m,0.5 m)位置处振动速度幅值进行观测,将本文方法所得结果与有限元方法所得结果对比,如图3所示。
如图2至图3所示,蓝色实线为本文方法计算结果(Current),红色虚线为有限元分析(Finite Element Analysis,图中采用符号“FEA”)计算结果,可以发现,在频率较高时两者存在一定偏差,而在低频带范围内吻合很好,验证了本文方法能够预测Winkler地基上板结构的响应幅值。
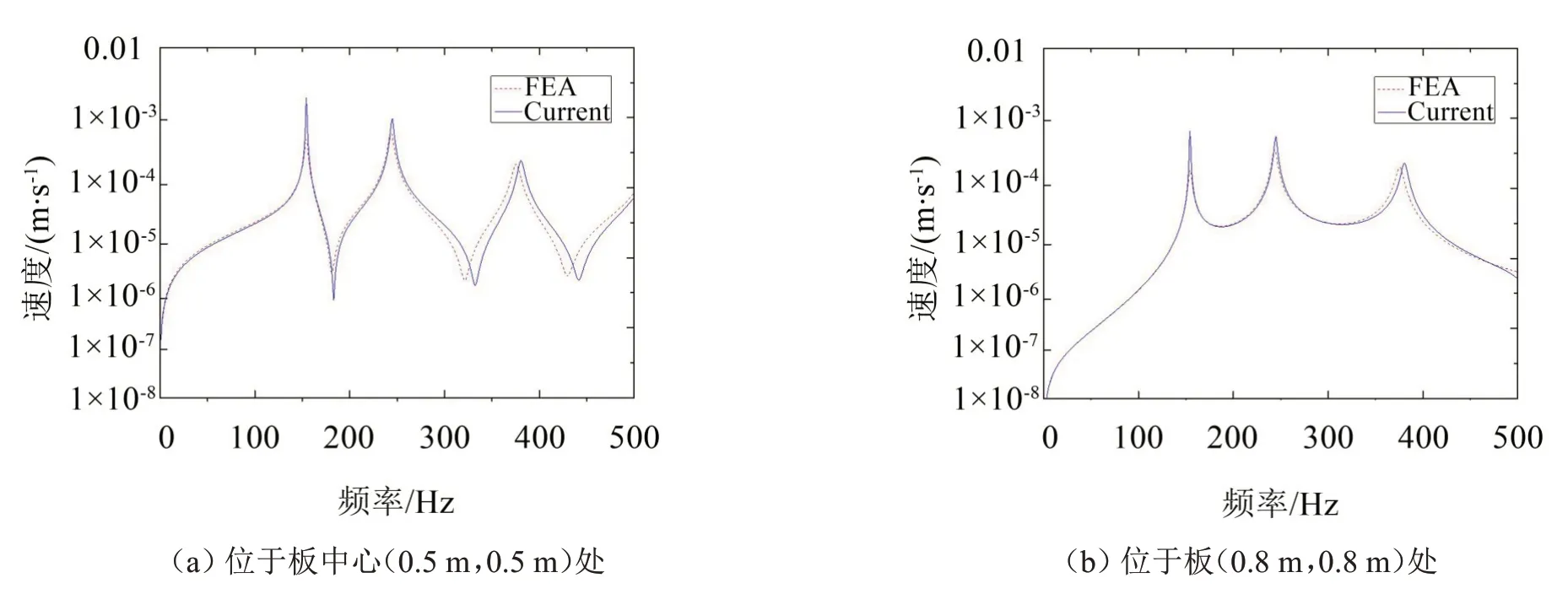
图2 施加于板中心位置(0.5 m,0.5 m)处横向集中力作用下不同位置振动速度的幅值
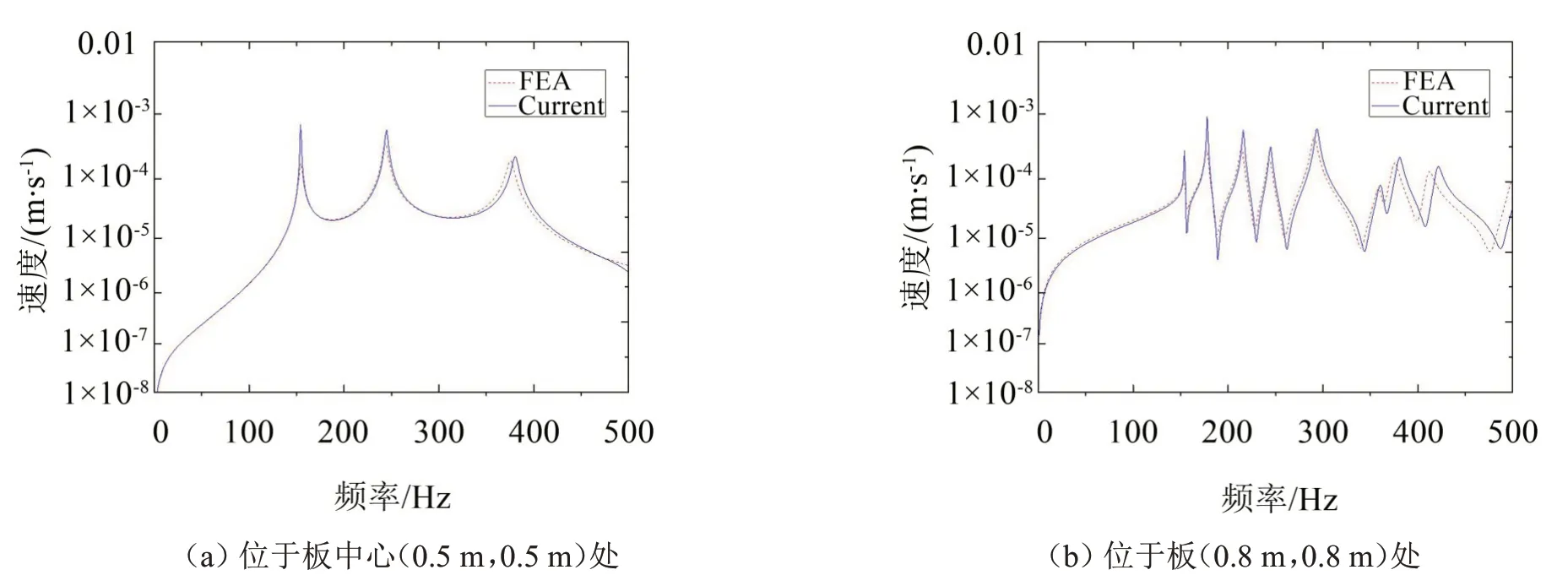
图3 施加于板(0.8 m,0.8 m)处横向集中力作用下不同位置振动速度的幅值
另外,对比图2 至图3 可以发现,在中心点处激励时,有较少的结构模态被激起;在非中心点处激励时,在中心点处有较少的结构模态被激起,在非中心点处有较多的结构模态被激起。出现上述特点是因为矩形薄板结构模态分布本身具有明显对称性,其中有些模态节线过中心点,因此在中心点处有更少的结构模态被激起。
将幅值为1 N、初相位ψ=arctan(4/3)的简谐横向集中力施加于板(0.8 m,0.8 m)位置处,在0~500 Hz频率范围内进行正弦扫描,同时对该作用点和(0.5 m,0.5 m)位置处振动速度的相位进行观测,将本文方法所得结果与与有限元方法所得结果对比,如图4所示。
如图4 所示,蓝色实线为本文方法计算结果(Current),红色虚线为有限元分析计算结果,可以发现,在较高频率和相位极值点两者存在一定偏差,两种结果在低频带范围内吻合较好,验证了本文方法能够在一定程度上预测Winkler 地基上板结构响应的相位。
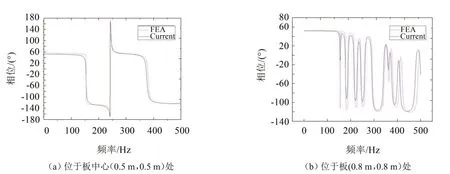
图4 施加于板(0.8 m,0.8 m)处横向集中力作用下不同位置振动速度的相位
3 结语
本文将改进傅里叶级数法运用到Winkler 地基上薄板的振动响应分析上,得到了响应的幅值与相位,并与有限元结果进行了对比,得到以下结论:
(1)在截断值M=N=6 时,基于本文方法所得固有频率结果已有较高精度,表明改进傅里叶级数法中假设的位移函数在求解域中足够光滑,且收敛速度快;
(2)在数值算例中给出了四边简支弹性地基上板结构的振动响应(幅值与相位),通过与有限元方法的结果比较,验证了本文方法的可行性和准确性;
(3)在中心点处激励,同时在中点处求解响应,共振峰数目减少。而在非中心点激励同时在非中心点处求解响应,会有最多的共振峰值。
