未知系统周期激励源分离方法的有效性分析

应祖光，倪一清，王友武

（1.浙江大学 航空航天学院力学系，杭州 310027；2. 香港理工大学 土木及环境工程学系 国家轨道交通工程技术研究香港分中心，香港 九龙）

复杂结构系统的故障诊断是一个重要的实际问题。复杂系统难以准确建模，因系统不确定或模型未知。系统故障导致结构变异，由此产生的激励（例如动力系统的偏心作用）需要诊断而且是未知的，同时环境动力激励也不确定或未知。已知信息仅为测量获得的系统响应。因此，形成一个基于测量响应的未知系统模型、未知激励的激励源分离或识别问题，系统与激励的双重未知性决定了其不同于传统问题，而具有一定的挑战性。解决此问题通常有两种途径，一种是综合利用先验概率和当前观测信息按照概率统计特性进行估计，另一种是仅用当前观测信息直接作估计，它更为简便，但相应方法需要可靠的理论基础。文献[1]给出一个基于测量响应2阶事件统计的信号源分离基本方法，文献[2]分析说明该方法可用于分离循环平稳信号源。文献[3]和[4]将该分离方法应用于多自由度系统，利用自由振动响应识别系统模态参数，文献[5]运用该方法结合小波变换法分离系统模态，但是分离方法要求测量响应个数不能少于自由度数。文献[6]讨论分离方法中联合对角化所用相关函数的时延选择，文献[7]说明该分离方法可较好地消除环境因素对于模态识别的影响，从而可将识别的系统模态用于健康监测。文献[8]将该分离方法应用于动力支承结构缺陷诊断，文献[9]和[10]给出该分离方法在齿轮传动机构、电动机系统的故障诊断等中的初步应用研究。然而，这些研究中尚存在一些基本问题，例如事件统计与时域统计概念混用、缺乏充分的分离有效性理论分析、实际模态数超过测点数、模态激励非独立源导致不满足方法条件等，它们给分离方法的有效应用与发展造成很大障碍。另外的分离方法例如独立分量法等也存在一定问题。因此，需要进一步对该源分离方法进行研究使其得到深入发展。

本文主要对基于测量响应的未知系统模型、未知激励的激励源分离有效性作理论分析，并基于时域统计说明分离方法的原理与条件。该分离方法先用测量所得响应构造时域相关函数，通过奇异值分解确定主要激励源相关特征值与特征变换，再通过联合对角化确定响应的激励源混合系数，从而得到分离的时域激励，同时给出周期激励源分离的有效性分析。然后，将该方法应用于多自由度振动系统，说明如何基于稳态响应分离出不同频率的激励。最后给出数值模拟及实验结果证实该基于响应的未知系统、未知激励的激励源分离效果与准确性。

1 源分离问题与分离方法有效性分析

以动力系统为例，稳态响应可表示为周期激励的线性组合，同时包含一定测量噪声，其关系的数学表达为：

式中：Y是k维响应向量，F是n维激励向量，H称为混合阵，表达各激励到响应的传递率关系，W是k维测量噪声向量，I是单位阵。式(1)所描述的激励源分离问题为：由测量响应Y确定未知的激励源F和混合阵H。该源分离问题的特点是系统与激励均未知。假定：(1)激励F中各周期源相互独立，即具有不同的频率；(2)噪声W中各元素为独立的白噪声，其均值均为零，且时域不相关；(3)测量响应数k大于或等于激励源数n。式(1)中，因激励源F幅值与混合阵H列向量为相乘关系，故源幅值不能直接确定，可设为单位值。

定义响应Y(t)与Y(t+τ)（τ为延时）的时域相关函数为：

式中：Ts是响应时长。类似地，可定义激励F的时域相关函数CF(τ)与噪声W的时域相关函数CW(τ)。通常Ts越大，相关函数值越稳定，周期函数没有事件统计特征但有时域相关值，随机噪声的时域相关函数当Ts很大时接近于事件统计值。

式(1)所描述激励源分离问题的分离方法包括如下两个主要部分。首先，根据响应相关函数的奇异值分解确定主要激励源的特征值，并对响应作特征变换。将式(1)代入式(2)得相关函数关系（τ=0时）：

基于假定，CF(0)与CW(0)分别接近于对角阵，其值相应于CY(0)的特征值，故由CY(0)的奇异值分解可确定其特征方向，大于一定值的特征值个数即为有效激励源数n。因YYT的维数大于或等于FFT，则CY(0)可能存在接近零的特征值，相应的特征空间可压缩。假定测量噪声强度相对较小，则其相应的特征值也较小，可从中消除。设CY(0)经奇异值分解并压缩后的特征值对角阵为Λ、正交阵为U，引入变换：

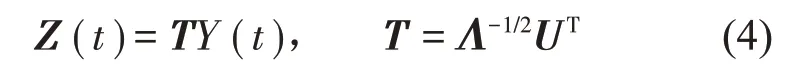
它将响应Y变换到激励F的特征方向，且有：

式中：Λ0与U0分别是CY(0)奇异值分解的压缩前特征值对角阵、正交阵，IF是单位阵。则变换后向量Z的相关函数具有单位特征值，激励源被均衡化，但仍然不能确定时域激励F和混合阵H。

其次，通过向量Z时延相关函数的联合对角化确定混合阵，从而得到分离的时域激励源。由式(4)和式(1)得时延相关函数：

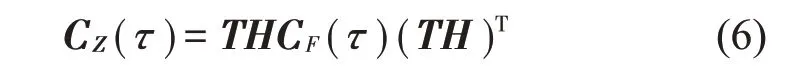
基于假定，噪声时域不相关故CW(τ)接近于零阵，而CF(τ)为对角阵，故可由CZ(τ)对角化的正交阵确定TH，得到混合阵H。然而，一个CZ(τ)对角化的正交阵是不确定的，需要多个CZ(τ)的联合对角化。选择m个延时τ=τ1,τ2,…,τm，对相关函数阵CZ(τ)进行联合对角化，即通过正交变换V使变换后VCZ(τi)VT的非对角元绝对值之和极小，确定正交阵V。则比较它与式(6)得：

于是，利用式(4)得到混合阵：

由式(1)得到激励源的估计：

总之，基于测量响应Y，构造时域相关函数，通过奇异值分解与联合对角化得到正交阵U和V，由式(8)和式(9)即可确定分离的未知激励源F和混合阵H。为保证分离效果，测量响应的采样频率需适当，太低可能遗漏高频激励，太高将增加测量噪声影响，采样时长需包含足够周期激励信息。

上述分离方法的重要基础是激励F的相关函数为对角阵，故其有效性主要取决于相关函数阵CF(τ)的特性。设周期激励源为：

式中：aj是幅值，θj是初相位，ωj是频率（其值对不同j不相等）。则CF(τ)的对角元为：

非对角元为：

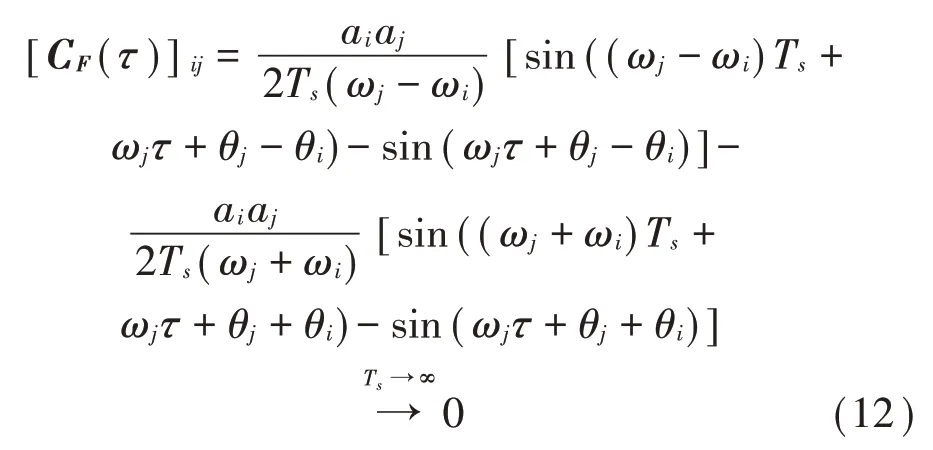
可见，相关函数阵CF(τ)随采样时长Ts增加而趋向于对角阵，从而保证分离有效。式(11)表明CF(τ)的对角元随时延呈周期性变化，故在前半周取延时τ值用于联合对角化即可。

2 振动系统的激励源分离与数值模拟、实验验证

设多自由度振动系统，方程为：

式中：X是位移向量，M、C、K分别是质量矩阵、阻尼矩阵与刚度矩阵，F是独立的激励向量，P是其位置参数阵。周期激励F第j个元素如式(10)所示，频率为ωj。则位移X的稳态响应为：

式中：P.j是P的第j列向量式(14)加上测量噪声即为式(1)，故可基于稳态响应按照上述方法分离未知激励源F，并确定混合阵H，获得各激励到响应的传递率关系。

数值模拟以3 自由度系统为例，设系统方程式(13)中无量纲质量M为单位阵，无量纲刚度阵：

瑞利阻尼C=0.02M+0.01K，两个无量纲激励参数a1=1，a2=0.5，ω1=0.9 rad•s-1，ω2=0.5 rad•s-1，θ1=0.349 rad，θ2=0，激励分别作用于第一自由度与第二自由度，测量噪声标准差为0.001。

通过模拟计算得到3个自由度的无量纲稳态响应如图1至图3所示，它们为非简单的周期响应。仅以该响应作为未知系统及激励的已知量，按照上述方法分离[即式(9)]可得到2 个无量纲激励源分别如图4、图5所示，它们为波形简单的周期源，通过傅里叶变换得其频率分别等于ω1、ω2，与系统周期激励频率完全一致，故图4 和图5 所示的分离结果为原激励，但注意到式(1)所描述激励源分离问题的特点，激励源与混合系数为相乘关系，其幅值可以包含在混合系数中，故不能确定。

图1 第一自由度响应x1

图2 第二自由度响应x2

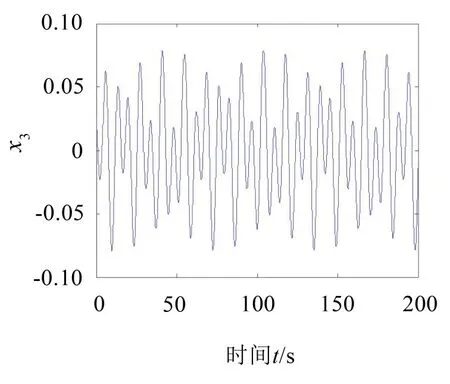
图3 第三自由度响应x3

图4 分离的第一激励源f1

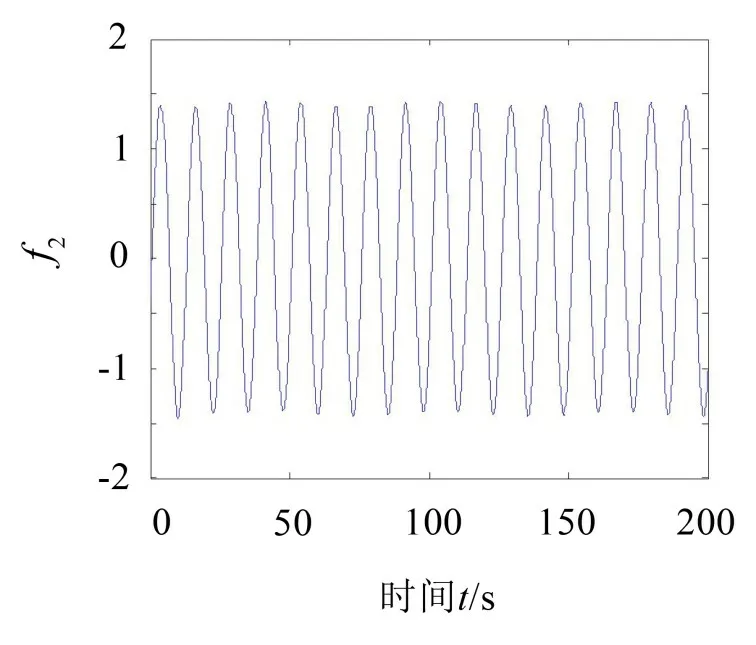
图5 分离的第二激励源f2

类似地，混合系数的绝对值也不能确定，但可归一化后比较确定其精度。通过分离得到式(8)的无量纲混合阵按第一行归一化后为：

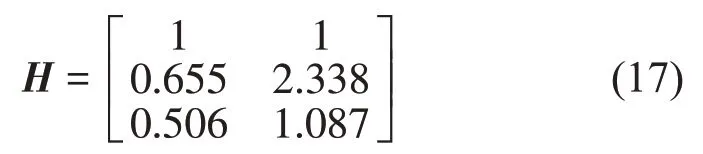
由式(14)和式(15)计算得到原系统的实际混合阵为：

比较可知混合系数的最大相对误差为5.8%，故分离得到的混合阵具有很好的精度。总之，上述方法能仅基于响应有效地分离出未知周期激励源，并较准确地确定混合系数，得到激励到响应的传递率关系。

此外，按响应相关函数与噪声相关函数之比的对数定义信噪比SNR，可得到通过分离确定的混合系数与信噪比的关系，图6 展示了混合阵H中第二行第一列元素h21随SNR 增加的变化，当SNR＞20时，其值基本保持恒定，说明该分离方法的鲁棒性。

图6 分离的混合系数h21随SNR变化

实验验证模型为图7所示的5层框架结构，基础固定，各层为集中质量，层间具有一定刚度与阻尼。第一层、第五层分别受到激振器的水平激励，各层的水平位移由激光传感器测量。根据上述分离方法，无需知道结构的具体情况。实验时，两个周期激励的频率分别为ω1=10 Hz，ω2=2 Hz，响应的采样频率为600 Hz。首先，测得第二层、第三层、第四层的位移响应分别如图8 至图10 所示，为非简单的周期响应。然后，仅以该响应作为已知量，按照上述方法分离得到2个无量纲激励源分别如图11、图12所示，再对其作傅里叶变换并转化为功率，得到功率谱分别如图13、图14 所示，可见它们为频率ω1、ω2的周期源，故为原结构的两个激励，其幅值包含在混合系数中。因此，该实验完全证实了在有效性条件下上述激励源分离方法的准确性。

图7 5层框架结构

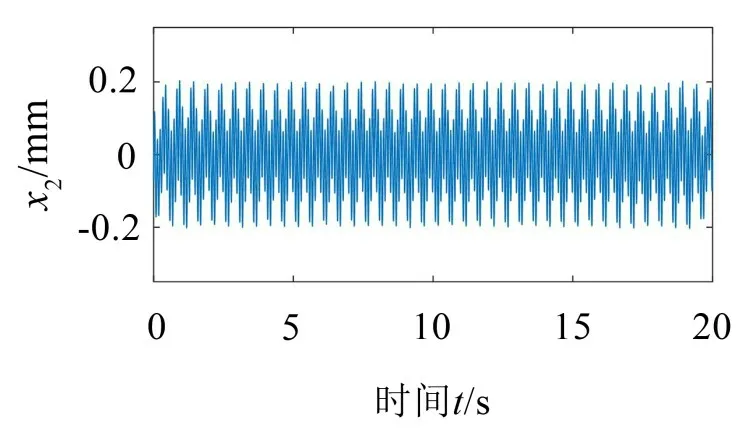
图8 第二层位移响应x2

图9 第三层位移响应x3

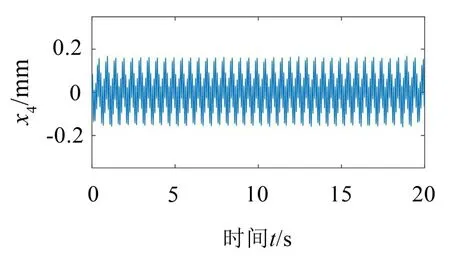
图10 第四层位移响应x4

图11 分离的第一激励源f1

图12 分离的第二激励源f2

图13 分离的第一激励源功率谱(PSD)

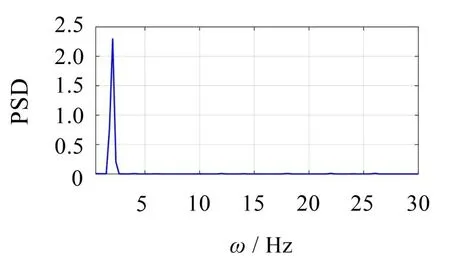
图14 分离的第二激励源功率谱(PSD)

3 结语

本文介绍了一种仅用测量响应的未知系统模型、未知激励的直接时域激励源分离方法，基于时域统计概念说明了该方法的原理与条件，并给出周期激励源分离的有效性理论分析。该分离方法包括两个主要部分：先用测量响应构造时域相关函数，由响应无时延相关函数的奇异值分解确定主要激励源的特征值，并对响应作特征变换；再利用将响应经特征变换后所得的向量构造时延相关函数，通过不同时延相关函数的联合对角化确定混合系数阵，从而得到分离的时域激励源。然后，将该方法应用于多自由度振动系统，阐述了如何基于稳态响应分离出不同频率的激励。最后通过数值模拟及实验证实了该基于响应的未知系统、未知激励的激励源分离方法的有效性、分离的时域激励与混合系数的准确性及对于测量噪声的鲁棒性等。