带两个不同半径环形刚性隔板的圆柱形储液罐内流体晃动特性研究

2021-12-15曹占雪王佳栋温国正

噪声与振动控制 2021年6期

曹占雪，王佳栋，温国正

（江苏大学土木工程与力学学院，江苏镇江 212013）

流体晃动是指部分充液的储液罐在外部激励作用下内部流体产生运动的现象。在实际工程中流体晃动产生的液动压力作用于结构，对其产生不可忽略的影响，例如唐山大地震中流体晃动使罐壁与底板之间的角焊处发生断裂破坏从而导致储油的泄露[1]，Tokachi-oki地震中流体晃动使储液罐浮顶下沉从而引发火灾[2]等。在工程上通常采用隔板降低流体晃动的幅度，从而减小了流体晃动对结构的影响；在理论上为获得流体晃动的各阶模态并服务于后续的动力学分析，有必要进行流体晃动的特性研究，因此研究储液罐中的流体晃动特性具有一定的工程应用和理论价值。

通过模态分析主要可获得储液系统的固有频率和各阶阵型，通过模态分析可以避免激励频率和储液系统的固有频率发生共振，从而为在工程上的应用提供依据。目前已有许多文献研究了隔板对流体晃动的影响，其中就包括模态分析，并已取得了丰硕的理论成果。Chu 等[3]研究了多个相同隔板条件下的流体晃动问题，发现系统的固有频率随着隔板上方的有效水深的变化而变化。Ebrahimian 等[4]用边界元法获得了轴对称储液系统的固有频率和振型，其研究表明隔板的位置对固有频率的影响更大。Wang等[5]对带有单个或多个相同隔板的环形储液系统进行了研究，发现隔板的位置主要对第1 阶模态的影响比较大。针对带单层隔板的渡槽，房忠洁等[6]用半解析方法说明隔板对速度势分布的影响比较大。有些学者对圆柱形储液系统进行了大量的研究，如杨唱等[7]通过对其研究发现隔板参数与防晃效果之间的关系。同样地，Wang 等[8]分析了多层相同隔板对流体晃动效应的影响。随着计算机技术的快速发展，数值模拟也经常被用来解决带隔板的储液系统中流体晃动问题。陈更等[9]对带隔板的液舱进行了数值模拟，其研究表明纵隔板可以更好抑制液舱中流体的晃动。Jin 等[10]通过数值模拟研究了水平多孔隔板附近的流体晃动特性问题，为理论研究提供了一个依据。

综上所述，这些文献主要研究了单个或多个相同隔板对流体晃动的影响，鲜有研究两个不同半径环形刚性隔板的控制机理，而文献[11]中的流体子域法是一种半解析法，能够同时满足求解问题的高效性和高精度，因此本文基于流体子域法研究了两个不同半径环形刚性隔板对流体晃动特性的影响。

文献[12]指出存在多层相同隔板的情况下，下层隔板对流体晃动的影响比较小，故本文在此主要考虑两层隔板情况，并且上隔板的内径大于下隔板，其目的是为了凸显下隔板对于晃动特性的影响。为了使所有的子域具有连续的边界条件，引入8 个人工界面将储液罐中的流体区域划分为8 个子域，利用叠加原理和分离变量法求出各子域的速度势的试函数，将其代入子域间的连续条件与自由液面的动力学边界条件，得到关于待定系数与晃动频率的级数方程，通过广义傅里叶展开将级数方程转换成线性方程组，从而得到关于频率与模态的特征方程。利用求解广义特征值的方法确定待定系数，从而使问题得到解决。

1 基本方程

图1 为带两层隔板的圆柱形储液罐，储液罐内半径为R3，上隔板内半径为R2，下层隔板内半径为R1。如图1 所示。R1、R2、R3满足关系：R1＜R2＜R3。本文主要研究储液罐中流体的晃动特性，因此罐体与隔板均假设为刚性。以储液罐底板的中心为坐标原点，建立如图1所示的柱体坐标系Orθz，上层隔板的位置设为z2，下层隔板的位置设为z1，液面高度设为H。

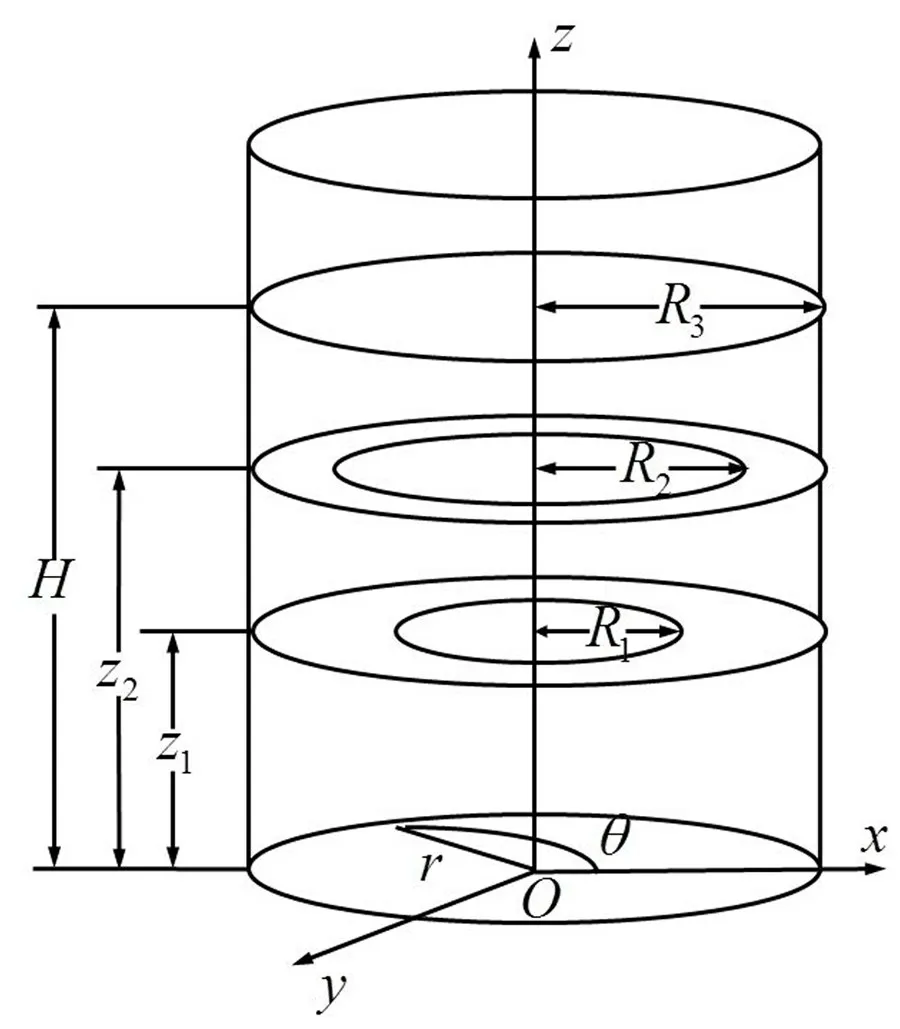
图1 带两层隔板的圆柱形储液罐

按照图2 所示的子域划分方法，将储液罐中的流体区域划分成8 个子域Ωi(i=1,2,…,8)，Sk(k=1,2…,8)为相邻子域间的人工界面。将子域Ωi的速度势函数设为φi，由于储液罐中的流体为无旋、无黏、不可压缩的理想流体，因此任意子域的速度势函数满足如下拉普拉斯方程：

在柱坐标系下，流体域Ωi中每一点的速度为[12]：

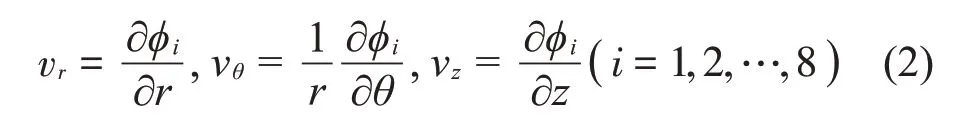
如图2所示。流体子域在流-固耦合界面上需满足固壁边界条件，因此各子域的速度势函数在罐壁上应满足如下边界条件：

图2 流体子域的划分

在罐底应满足如下边界条件：

在隔板上应满足如下边界条件：

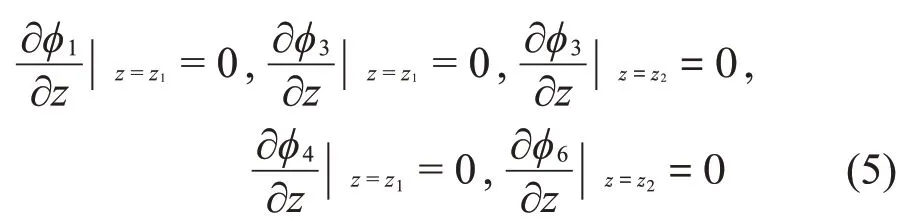
柱形子域的速度势函数应满足如下边界条件：

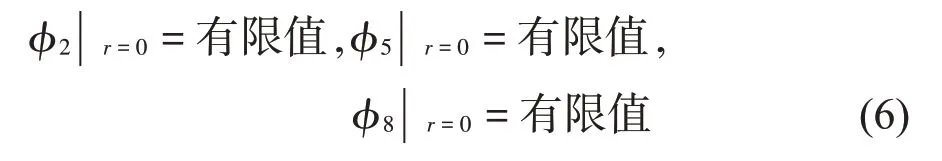
本文考虑流体做微幅线性晃动，根据Bernoulli方程，流体子域Ω6、Ω7以及Ω8在自由液面上应满足如下边界条件：

相邻子域在其界面上应该满足压力及速度连续条件，即有：

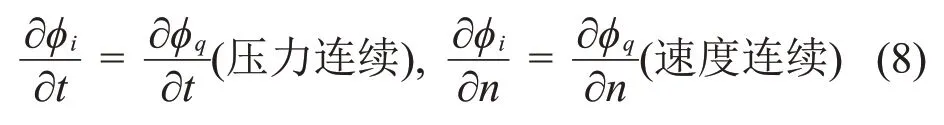
式中：n为人工界面Sk上的法向单位矢量；i、q为相邻的子域。

2 子域速度势函数求解

当储液罐中流体发生自由晃动时，可以将流体速度势函数设为如下形式[13]：

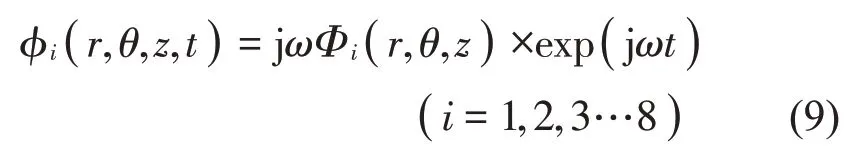
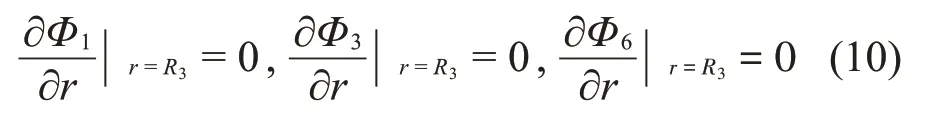
在罐底应满足如下边界条件：

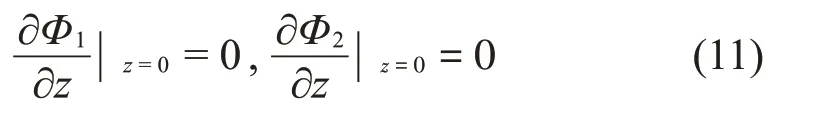
在隔板上应满足如下边界条件：

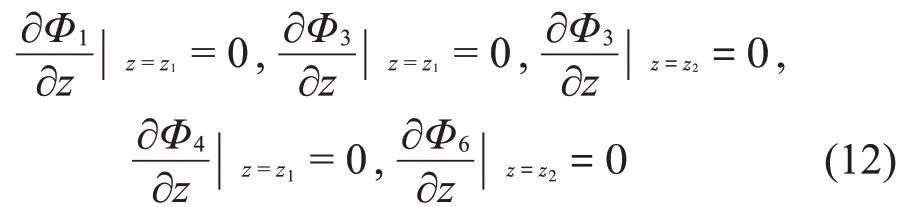
位于中心区域的速度势函数应满足如下边界条件：

Φ2|r=0=有限值,Φ5|r=0=有限值。

流体子域Ω6、Ω7以及Ω8的振型函数在自由液面上应满足如下边界条件：

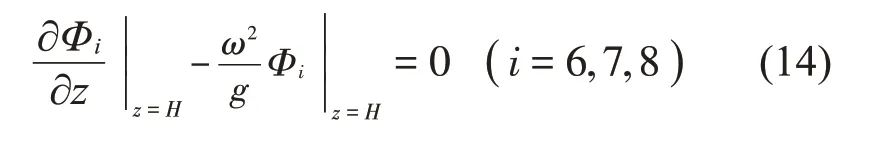
相邻子域在其界面上应该满足压力及速度连续条件，即有：

式中：n为人工界面Sk上的法向单位矢量；i、q为相邻的子域。

根据叠加原理，对各子域的振型函数进行分解，结果如图3 所示，图3(a)所示为环柱形子域，图3(b)所示为柱形子域，图3(a)中的细点画线表示子域的对称轴。子域6、7、8 中的上实线为零压力边界条件，其余所有实线均为刚性边界条件，虚线代表非齐次性边界条件，即有：

图3 振型函数分解示意图

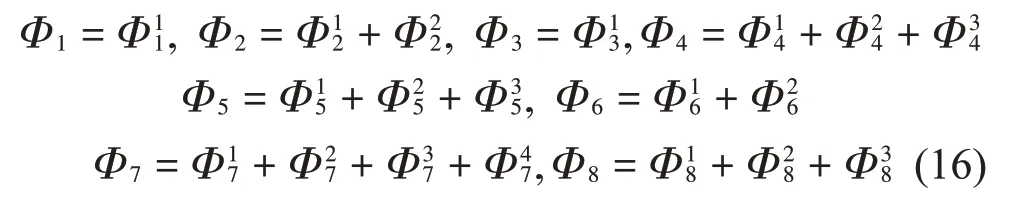
根据式(16)，对于子域Ω1，振型函数的分量Φ11应满足如下边界条件：

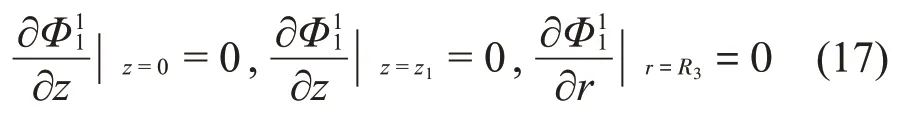
对于子域Ω2，振型函数的分量Φ12、Φ22应满足如下边界条件：

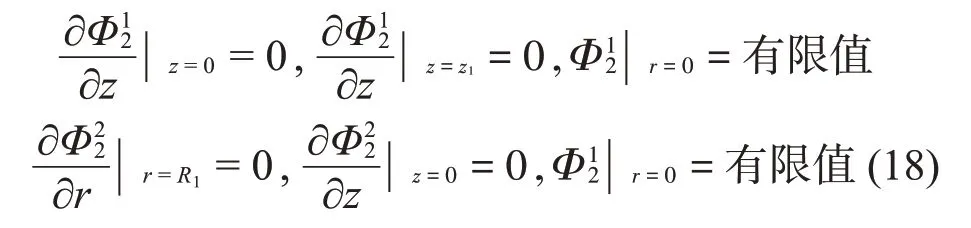
对于子域Ω3，振型函数的分量Φ13应满足如下边界条件：

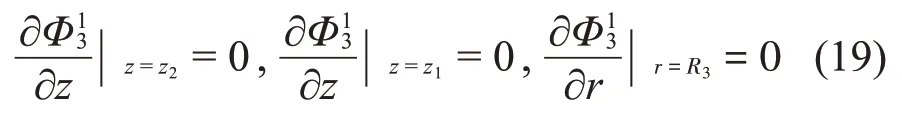
对于子域Ω4，振型函数的分量Φ14、Φ24、Φ34应满足如下边界条件：

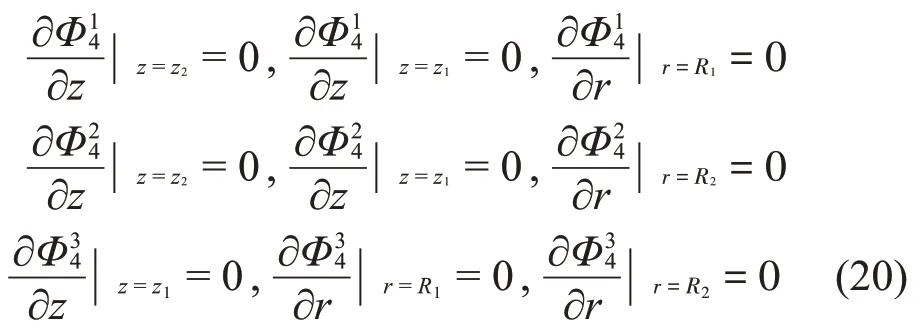
对于子域Ω5，振型函数的分量Φ15、Φ25、Φ35应满足如下边界条件：

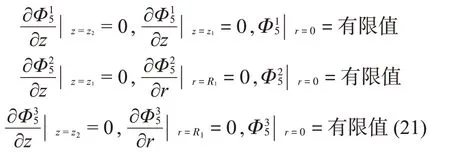
对于子域Ω6，振型函数的分量Φ16、Φ26应满足如下边界条件：

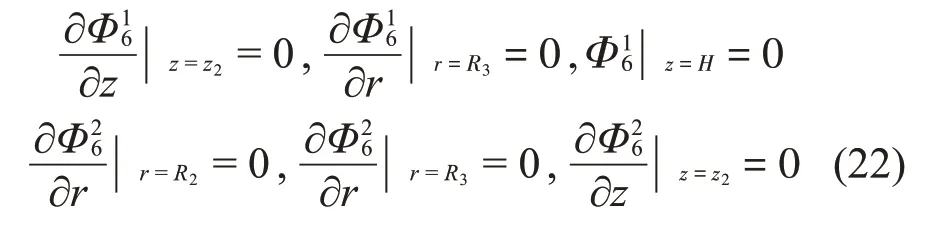
对于子域Ω7，振型函数的分量Φ17、Φ27、Φ37、Φ47应满足如下边界条件：

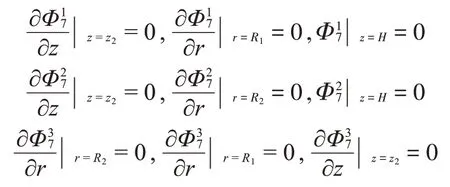
对于子域Ω8，振型函数Φ18、Φ28、Φ38应满足如下边界条件：

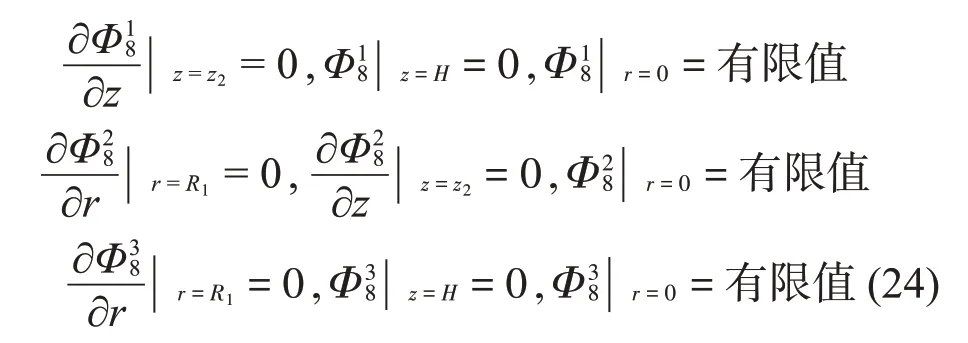
根据式(17)至式(24)，利用分离变量法可求得各个分量的试函数，再根据式(16)可得各个子域振型函数的形式解。将振型函数代入式(14)～式(15)中可以得到19 个级数线性方程组。根据三角函数和贝塞尔函数的正交性，消除级数方程中的空间坐标，并将方程截断至N，从而得到有关待定系数的线性方程组，即有：

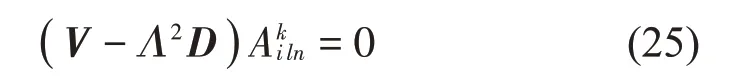
式中，矩阵V、D中的非零元素为级数方程展开后的系数；Λ为无量纲化后的晃动频率，满足：

级数方程(25)中的Λ2定义为广义特征值，通过求解广义特征值的方法确定和的数值。将代入振型函数就可以确定各个子域的速度势函数。

3 收敛性和比较研究

首先进行收敛性分析，表1和表2分别对应于上层隔板参数变化时的前3 阶晃动频率，从表中可以发现，随着截断项数的增加，晃动频率会逐渐趋于精确解。虽然隔板参数对晃动频率的收敛性会有一定的影响，但这种影响会随着截断项数的增加而逐渐减小，当截断项数足够大时，该影响可忽略不计。当N=26时，表1和表2中的晃动频率均可保证4位有效数字，因此在下面的分析中，截断项数均取26。

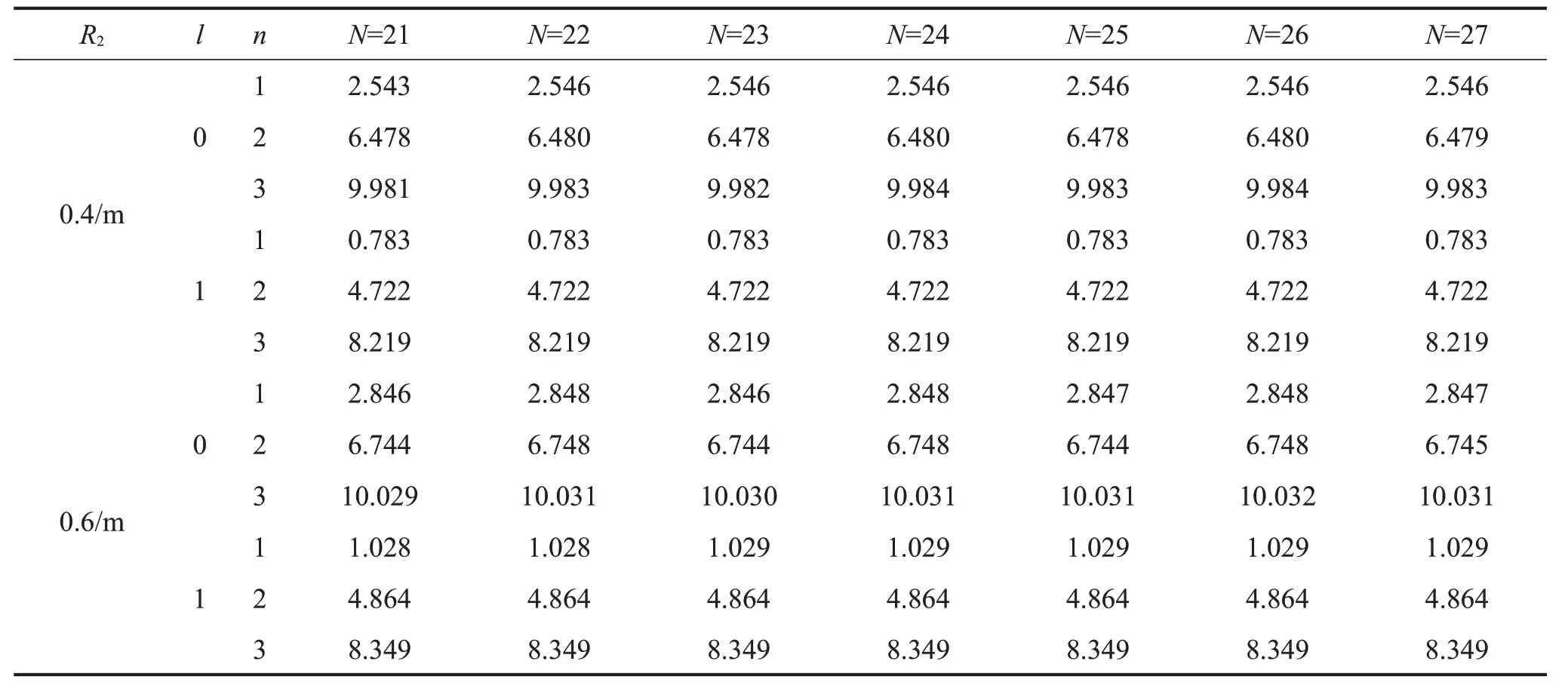
表1 (l=0,1,n=1,2,3)随截断项数N变化的收敛性（R1=0.2/m;R3=1/m;z1=0.4/m;z2=0.8/m;H=1/m)

R2 0.4/m 0.6/m l 0 1 0 1 n 1 2 3 1 2 3 1 2 3 1 2 3 N=21 2.543 6.478 9.981 0.783 4.722 8.219 2.846 6.744 10.029 1.028 4.864 8.349 N=22 2.546 6.480 9.983 0.783 4.722 8.219 2.848 6.748 10.031 1.028 4.864 8.349 N=23 2.546 6.478 9.982 0.783 4.722 8.219 2.846 6.744 10.030 1.029 4.864 8.349 N=24 2.546 6.480 9.984 0.783 4.722 8.219 2.848 6.748 10.031 1.029 4.864 8.349 N=25 2.546 6.478 9.983 0.783 4.722 8.219 2.847 6.744 10.031 1.029 4.864 8.349 N=26 2.546 6.480 9.984 0.783 4.722 8.219 2.848 6.748 10.032 1.029 4.864 8.349 N=27 2.546 6.479 9.983 0.783 4.722 8.219 2.847 6.745 10.031 1.029 4.864 8.349

表2 (l=0,1,n=1,2,3)随截断项数N变化的收敛性（R1=0.3/m;R2=0.6/m;R3=1/m;z1=0.2/m;H=1/m）

z2 0.4/m 0.8/m l 0 1 0 1 n 1 2 3 1 2 3 1 2 3 1 2 3 N=21 3.772 6.996 10.137 1.598 5.315 8.529 2.851 6.749 10.030 1.063 4.918 8.349 N=22 3.774 6.998 10.141 1.598 5.316 8.529 2.853 6.753 10.031 1.063 4.918 8.350 N=23 3.773 6.999 10.144 1.598 5.317 8.530 2.851 6.750 10.031 1.063 4.918 8.350 N=24 3.775 7.001 10.147 1.598 5.317 8.531 2.853 6.754 10.031 1.063 4.918 8.350 N=25 3.774 7.002 10.149 1.598 5.318 8.531 2.852 6.751 10.031 1.063 4.918 8.350 N=26 3.775 7.003 10.151 1.598 5.318 8.531 2.853 6.754 10.032 1.064 4.918 8.350 N=27 3.775 7.004 10.153 1.598 5.318 8.532 2.852 6.751 10.032 1.064 4.918 8.350

为验证本文方法的正确性，使用通用有限元软件ADINA对本文模型进行模态分析，得到了流体晃动的频率和模态。表3 对本文方法解和ADINA 解进行了比较。结果表明，本文计算的结果和ADINA有限元软件模拟的结果具有较好的一致性，其最大相对误差为0.65%，最小相对误差为0.02%。因此本文方法满足求解问题的高精度要求。

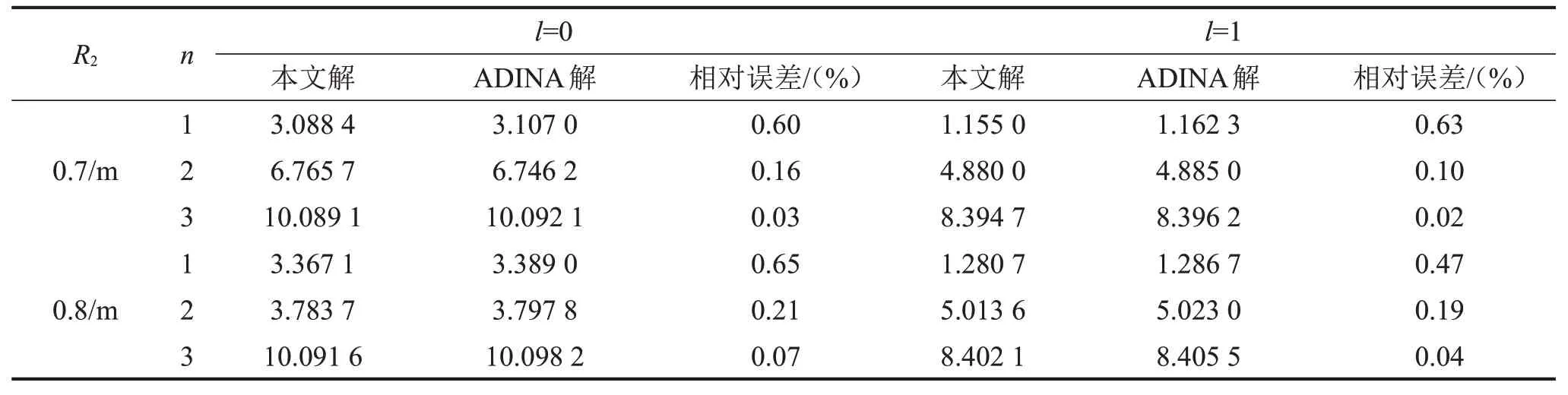
表3 (l=0,1,n=1,2,3)的比较研究（R1=0.35/m;R3=1/m;z1=0.5/m;z2=0.8/m;H=1/m）

R2 0.7/m 0.8/m n 1 2 3 1 2 3 l=0本文解3.088 4 6.765 7 10.089 1 3.367 1 3.783 7 10.091 6 ADINA解3.107 0 6.746 2 10.092 1 3.389 0 3.797 8 10.098 2相对误差/（%）0.60 0.16 0.03 0.65 0.21 0.07 l=1本文解1.155 0 4.880 0 8.394 7 1.280 7 5.013 6 8.402 1 ADINA解1.162 3 4.885 0 8.396 2 1.286 7 5.023 0 8.405 5相对误差/（%）0.63 0.10 0.02 0.47 0.19 0.04

4 参数研究

首先研究了上层隔板内半径和上层隔板位置对流体晃动特性的影响，结果如图4和图5所示。从图中发现，当上层隔板的内半径接近储液罐的内半径时，晃动频率将不再受上层隔板的影响，此时下层隔板对流体晃动的频率起主导影响。但当隔板的位置靠近自由液面时，图5中曲线的斜率降低很快，表明上层隔板的位置是影响流体晃动最主要的因素。因此对上层隔板的位置进行优化设计能够有效减弱流体的晃动。

图4 Λ2l1(l=0,1)随上层隔板内径的变化曲线（R1=0.2/m;R3=1/m;z1=0.2/m;H=1/m）

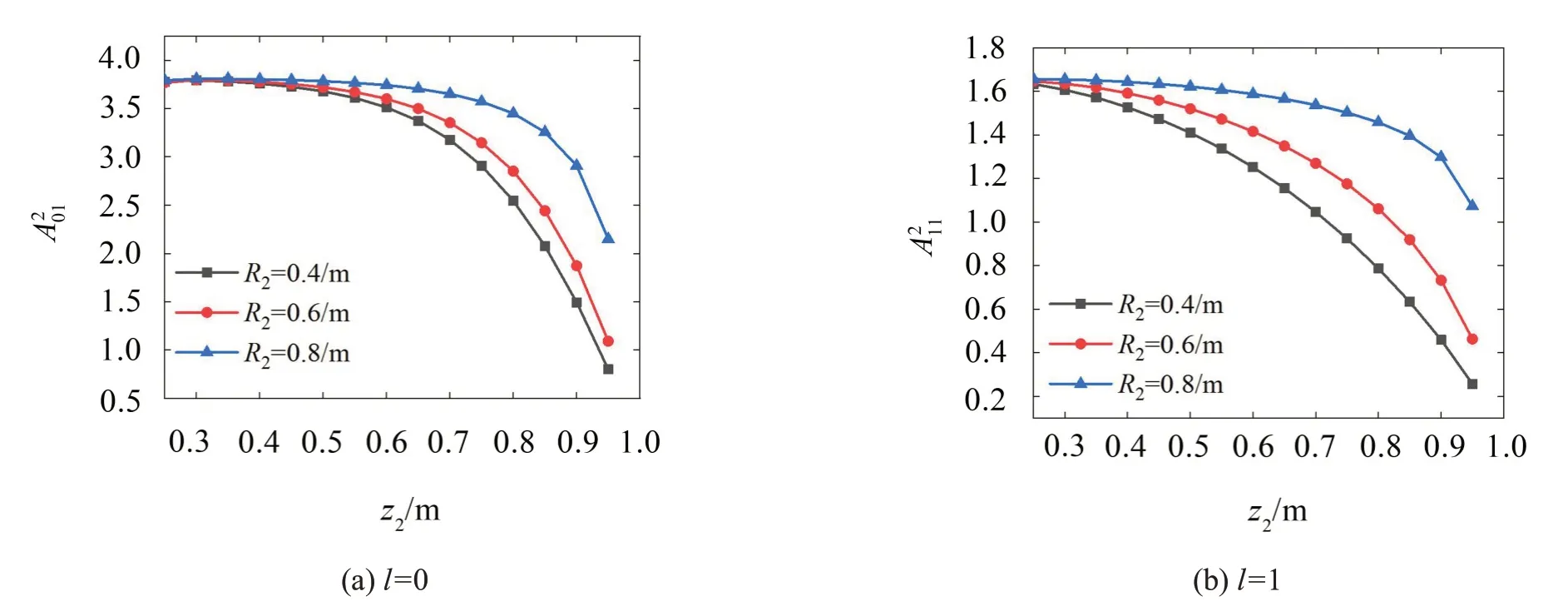
图5 (l=0,1)随上层隔板位置的变化曲线（R1=0.2/m;R3=1/m;z1=0.2/m;H=1/m）

其次研究了下层隔板内半径和下层隔板位置对流体晃动的影响，结果如图6和图7所示。下层隔板内半径对晃动频率的影响随着隔板位置的降低而减小，而这主要因为隔板接近于罐底时，隔板对流体晃动的影响很小。但当下层隔板的内半径逐渐减小时，对晃动频率的影响也就越来越明显。因此改变下层隔板的内半径仍然能够明显降低流体晃动的固有频率，即也可达到抑制流体晃动的目的。

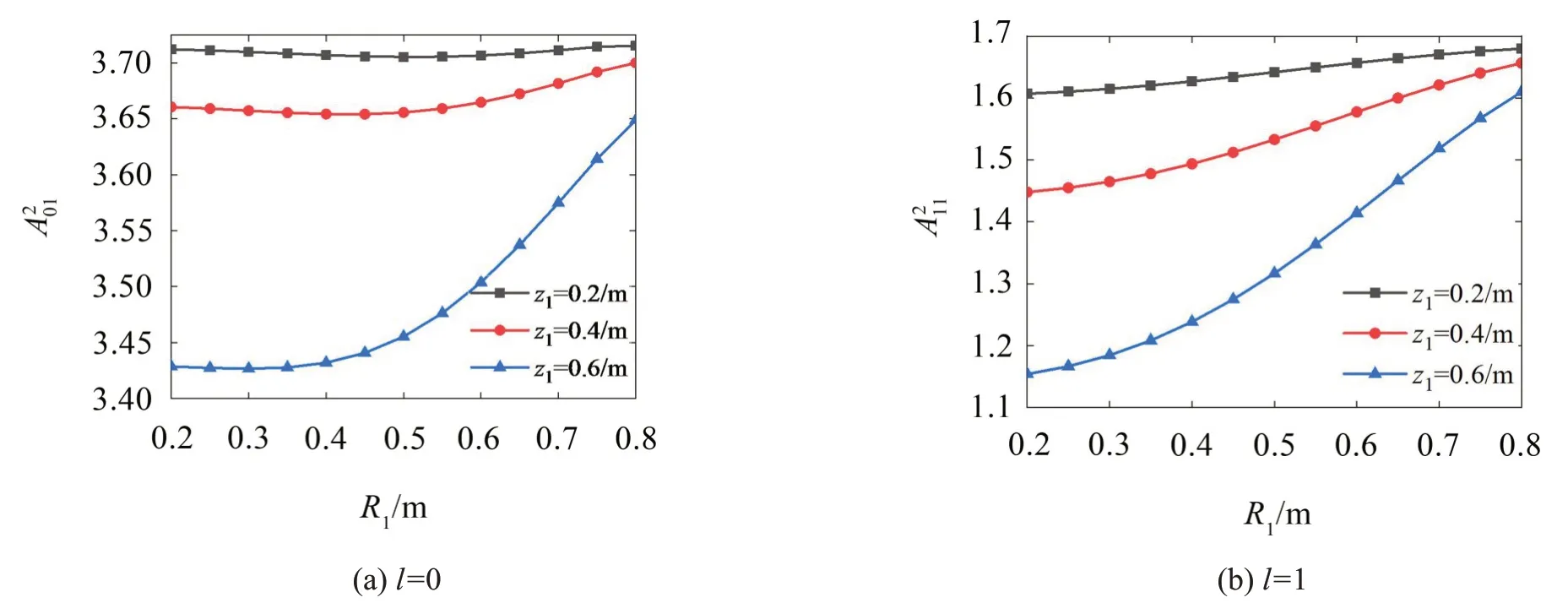
图6 (l=0,1)随下层隔板内径的变化曲线（R2=0.9/m;R3=1/m;z2=0.8/m;H=1/m）

图7 (l=0,1)随下层隔板位置的变化曲线（R2=0.7/m;R3=1/m;z2=0.85/m;H=1/m）

将求得的流体晃动频率代入方程式(25)就可以确定待定系数，将各个子域的振型函数代入方程式(9)就可以确定各个子域的速度势函数。图8和图9 分别为环向波数为0 和1 的前两阶振型。很明显，当环向波数为0时其表现为对称振型，当环向波数为1时表现为反对称振型。

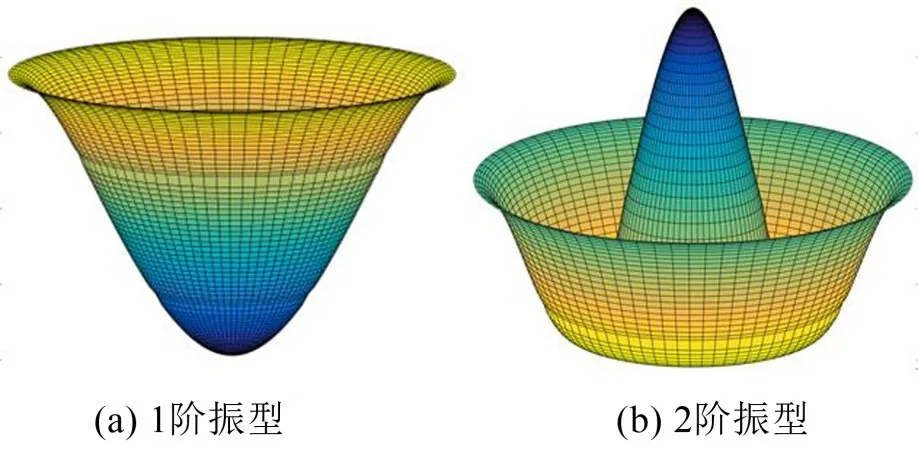
图8 环向波数为0时的前两阶振型（R1=0.35/m;R2=0.7/m;R3=1/m;z1=0.5/m;z2=0.8/m;H=1/m）

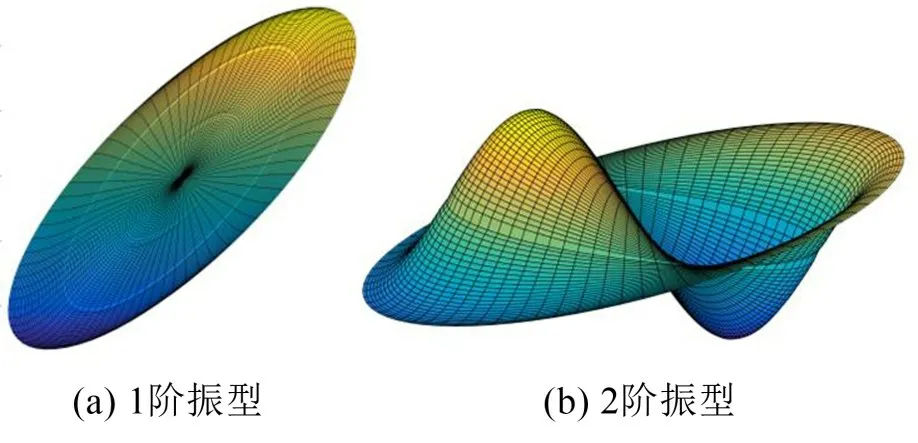
图9 环向波数为1时的前两阶振型（R1=0.35/m;R2=0.7/m;R3=1/m;z1=0.5/m;z2=0.8/m;H=1/m）

5 结语

本文的主要创新点在于研究了两个不同半径环形刚性隔板对流体晃动的影响，文中隔板及罐壁均采用刚性材料，流体为理想流体。通过流体子域法求解了各个子域的速度势函数，并与ADINA解进行比较验证了本文方法的正确性，进而对流体的晃动特性进行了研究。本文中的模型只适合于流体做微幅线性晃动的情况。虽然本文的研究对象为带两层不同内径环形刚性隔板的储液系统，但本文的研究方法可以进一步扩展到带有任意个不同内径隔板的情况。

通过对参数的研究可以得到以下结论：存在两层隔板的情况下，下层隔板的内径越小，对流体晃动的影响越明显，但当下层隔板位置靠近罐底时，隔板内径的变化对流体晃动的影响越来越小；下层隔板内径越小，对环向波数l=0的影响越小。