数感的修订变化与内涵认识

林胜威

数感的修订变化与内涵认识

林胜威

（化州市新安中学，广东 茂名 525133）

由于观点的双重叠合造成数感认识的模糊；从数感的提出到修订体现了中国教育价值取向从知识立意到能力立意，再到素养立意的转变历程；通过梳理学者的论述，可从3个维度认识数感的内涵：直觉能力为基础、活动感悟为过程、态度意识为目标；数感的培养可从“数与数量及数量关系”和“运算结果的估计”两方面进行．

数感；数感内涵；认识维度；数感培养

1 问题背景

数感作为《义务教育阶段数学课程标准（2011年版）》（以下简称《课程标准》）10个基本素养之一，在2001年的《全日制义务教育数学课程标准（实验稿）》（以下简称《课程标准（实验稿）》）中第一次提出，当即引起了广泛的关注和激烈的讨论（详见文[1-8]）．《课程标准》对数感进行了修订，明确了数感的内涵，研究方向从内涵研究转向实践研究．但一线教师，承担着培养数感的主要任务，对数感内涵的理解却是模糊的．有学者通过对近五百名小学一线教师有关数感内容的调查与访谈发现，90%以上的教师知道数感这一核心概念，但不知道“数感”是什么[9]．有教师认为[10]，数感是比较模糊的，有些数学内容甚至“只可意会，不可言传”，“数感”一词已提出了十余年，它一直徘徊在教学的边缘．这或许是教育部在2019年连续发布两份重要文件的原因所在．第一份是《中小学幼儿园教师培训课程指导标准（义务教育数学学科教学）》，它指出[11]：中小学数学教师培训的依据是《课程标准》的理念和目标，培训目标（一级指标）的确定主要参考《课程标准》划分的各内容领域；第二份是《教育部关于加强初中学业水平考试命题工作的意见》，它指出取消《初中学业水平考试大纲》，严格依据义务教育课程标准进行科学命题．因此，无论从国家课程改革，还是一线教师教学的需要，都有必要对数感概念进行回顾与审视．

2 数感认识模糊的可能原因

数感之所以会引起学者的争议与及一线教师的模糊认识，除了因英文的翻译而造成的歧义（无论是从内容的角度还是从英文原文的角度，都不支持“数感”与“符号感”的提法，建议改为“数观念”与“符号观念”[3]），更主要的原因是不同观点的双重叠合．

2.1 心理学与教育学的叠合

1954年，Dantzig首次提出数感的概念，并且将数感看作是对细小的数量变化的一种直觉感受[12]．1980年，美国心理学家Prentice Starkey对16周到30周大的婴儿做实验发现[13]：婴儿能觉察到2个点到3个点的数量变化；这种觉察点数量变化的能力，婴儿不可能在出生后几个月时间内从外界环境学到，而应该是一种人类遗传能力．由此可见，作为心理学术语的数感，指的是一种对小数量物体变化的先天感觉．作为数学教育术语的数感采用与心理学术语相同的名词表述，但教育的目的与功能是促进人的发展，那么在教育学中数感则不应局限于这种先天的数量感觉能力，而应该包括通过后天的学习而形成的能力．如美国2000年的“美国数学课程标准”就将Number Sense的能力水平分为4个层次：脱离实物用数进行思考、能把数与实物模型联系起来、能进行较为复杂的有关数的推理、能自然地发现和使用运算性质和认识等量代换等性质[7]．由此可见，数感一词既有来自心理学的意义，也有教育学方面的思虑，从而造成对其认识的模糊．不过，这也揭示了对数感的认识和培养既要基于心理学的发现和认识，也要站在促进人能力发展的角度．

2.2 意识形态与学科教学的叠合

《课程标准》作为国家教育的纲领性文件，是学科教学的标准与导向，必然包含有国家意识形态，也即蕴含着“培养什么人、怎样培养人、为谁培养人”等根本问题的思考．因此，对数感的认识与理解必须结合国家教育方针政策，也即是国家的意识形态．在以培养学生的核心素养为目标的要求下，数感作为《课程标准》明确注重培养的十大素养之一，必然成为学生能够适应终身发展和社会发展需要的必备品格和关键能力．另外，数感作为数学教育名词，必然要以数学学科为背景，要实施数感的培养首先要弄清楚数感在数学学科中的地位与作用，与其它数学能力的关系，数感是一种数学感觉？还是一种数学能力？抑或是一种数学观念？也即是学术层面．所以，对数感的认识与理解既要基于数学学科的发展研究，又要结合国家各时期教育的意识形态及价值取向．

3 数感表述修订的两个变化

3.1 数感表述的变化

在初次提出数感之时，国内对其了解不多，缺乏系统深入的研究，主要是参考了西方国家的论述，如2000年美国的《学校数学课程与评估的标准》：“number sense”是伴随着学生对数、数的表示方式、数之间的关系和数系统的理解以及数运算、运算律等的理解和运用而逐步发展的[7]．《课程标准（实验稿）》只是指出数感的外延，未对其内涵进行界定．经过近10年的实践与研究，对数感的认识逐渐清晰，并且教育理念随着课程改革的深入也发生了变化，因而对数感的理解也有所变化．两者具体描述如表1．

表1 两个版本的标准对数感描述的比较

通过对比，修订前后出现了内容的“减”与“增”变化：

（1）“减”．修订后的数感删减了“多种方法表示数”“选择适当的算法”和“对结果的合理性作出解释”的表述．首先，“多种方法表示数”是数的表示方式，属于符号的表示与运用，修订后将它纳入“符号意识”：能够理解并且运用符号表示数、数量关系和变化规律．其次，“选择适当的算法”和“对结果的合理性作出解释”实质是对算理的理解、对合理简洁算法的寻求和运算结果的估计，修订后将其纳入“运算能力”．经过删减调整，收缩了数感外延，使数感的范围由松散变得集中，对象的指向也更加明晰．

（2）“增”．在“数”基础上增加“数量”成为“数与数量”．数量是有实际背景的关于量的多少的表达，是对现实生活中事物的抽象；数是对数量的抽象，数的关系是对数量关系的抽象[16]．例如数字“1”是基于对“1支粉笔”“1个苹果”“1朵花”……的抽象；“1<2”是基于“1支粉笔比2支粉笔少”“1个苹果比2个苹果少”……的抽象．可以说，对“数”意义的感悟是以“数量”为基础，计算技能（如“数数”）的习得也始于对实物数量的操作（如“点手指”或“数石子”）．这种变化说明，对数感的理解已不限于数感的能力要求，同时增加了对数感来源的认识．另一方面，既然对“数”意义的理解源于生活实践，那么“实践活动经验（也包括数学活动经验）”就是获得数学知识、数学技能、数学思想方法的前提，这恰好也体现了课程标准的理念由“双基（基本知识、基本技能）向“四基（基本知识、基本技能、基本思想、基本活动经验）”的转变．

3.2 价值取向的转变

在《课程标准（实验稿）》颁布之前，没有提出数感的概念，义务教育阶段的数学教学注重基础知识的教学、基本技能的训练（双基），对学生数学能力的评价主要以数学知识的掌握程度和数学技能的熟练程度，教育价值取向处于“知识立意”阶段．《课程标准（实验稿）》首次提出数感培养，主要表现为“理解数的意义；能……并对结果的合理性作出解释”．这是一种功能性的表述，也就是通过数感的培养让学生具有什么能力、达到什么水平，是一种“能力立意”的价值取向，反映当时中国教育对“高分低能”的摒弃，开始注重学生素质能力的培养，是“素质教育”的肇始．《课程标准》对数感的表述为“数感主要是……的感悟”，是一种概念性的表述，指出数感是什么．从某种程度上讲，素养不是直接教出来的，而是学生自己悟出来的[17]．那么通过数感的培养让学生有“感悟”，“感悟”所得内化成有助于学生终身发展的必备品格和关键能力，就成为学生的数学核心素养，这符合“素养立意”的教育价值取向．所以，以课程标准的颁布为时间节点，中国教育价值取向可分3个阶段：知识立意阶段、能力立意阶段、素养立意阶段（见图1）．在素养立意之下的数感培养，就不能凭一道题、一次训练、一节课而达成，而应贯穿整个数学学习的始终，渗透于数学教学的各个方面；并且数感的培养又可以促进学生数学的学习，成为学生数学能力形成的基础和关键．

图1 价值取向阶段划分

4 数感内涵认识的3个维度

2001—2011年期间，许多学者从不同视角对“什么是数感”展开研究，得出许多不同观点和认识，大致分为3种：态度意识说、直觉能力说和活动感悟说．

4.1 态度意识说

持有此观点的学者认为，数感是一种主动地、自觉地或自动化地理解数和运用数的态度与意识[2]；数感是对数字关系和数字模式的意识，以及运用这种意识灵活地解决数字问题的能力，学生具有“数感”的典型特征就是他们能够对其所面对的数字模式、数字关系和计算过程进行归纳，并能够把新知识和已有知识联系起来[8]．

在心理学上，态度是指由认知、情感、意向3个因素构成的、比较持久的个人的内在心理倾向[18]；意识是指人以感觉、知觉、记忆和思维等心理活动过程为基础，系统地对自身状态和外界环境变化的觉知[18]．那么，数感是指人对“数字、数字关系、数字模式”的一种主动或自动的觉知，是运用“数字”（或“数学”）思考问题的心理（或思维）倾向．具有数感的人，常常将有关问题与数联系起来，用数学的方式思考问题；而所谓“用数学的方式思考问题”，按美国学者Grouws的观点，是指形成数学化和抽象化的数学观点，运用数学进行预测的能力，以及运用数学工具解决现实问题的能力[1]．根据何小亚教授的观点，数学意识是个体在思考问题时在数学方面的自觉意识或思维习惯，是用数学的眼光看世界的具体内容[19]．那么，将“数感”称为“数字意识”或“数学态度”，可能更能反映其本质及内涵．

4.2 直觉能力说

持有此观点的学者认为，“数感是一种‘直感’能力，是对于客观事物和现象数量方面的敏感性，及相关的鉴别（鉴赏）能力”[2]；“狭义的数感就是数字感，即人脑对于数字或数字运算定律的直觉；广义的数感就是数学感，即人脑对于数学对象的直觉”[6]．

直感即是直觉，直接感觉．直觉是不经过有意识逻辑推理而识别或了解事物的能力；与之相对的是逻辑分析能力、有意识的认知加工活动[20]．认知心理学的研究发现，人脑中并存着两种不同的信息加工系统，即意识加工与无意识加工；其中，无意识加工是一种基于技能与经验的自动化的、无需意志努力的加工[21]．直觉属于无意识认知加工．所以，人可以快速地预测问题的答案，但又往往“说不清、道不明”得到答案的具体过程．数感是对数的直觉能力，在不经过精确的计算加工或逻辑推理之前，就能感知数的大小、估计运算结果、灵活选择算法等．这种对数字的“直觉”能迅速地反应成数学问题，使数学问题从感知层面敏捷地链接到数学思维，从而有助于形成问题解决策略[8]．

4.3 活动感悟说

持有此观点的学者认为[7]，“数感”是对数的“感悟”．“感”是外界刺激作用于主体而产生的，是通过肢体（如感官等）而不是通过大脑思维，它含有原始的、经验性的成分．悟是主体自身的，是通过大脑思维而产生的．“感悟”既通过肢体又通过大脑，因此，既含有感知的成分又有思维的成分．数感的建立开始更多地依靠经验的积累，到一定程度后靠经验、理性的叠加，而后形成观念．

既然外界的刺激作用产生“感”，那么“感”是指“感觉”之意．感觉是指大脑对直接作用于感觉器官的客观事物的个别属性的反映[18]．数字符号是一种抽象的形式化语言，在没有理解其含义之前，它只是一种毫无意义的图形，当然无法引起人体感觉器官的“注意”或“感觉”．那么，对“数”的感悟可能指的是对“数学活动”的反映之后的“悟”．皮亚杰的反思性抽象理论指出，在儿童对物质世界的感知和行动上有两种不同的抽象形式：一是经验性抽象，直接来源于客观对象本身及性质；二是伪经验性抽象，来自作用在客体对象上的行动[22]．“悟”是一种“伪经验性抽象”，是对“数学活动”的抽象、归纳、反思．所以，“感悟”不是指“既通过肢体又通过大脑”“既含有感知的成分又有思维的成分”，而是指对数学活动的抽象、归纳、反思，而形成对数学知识、方法、思想的领悟．这可能更符合史宁中所述“感悟”的本意：这里之所以用“感悟”这个词，是因为有许多能力不是仅仅通过书本的学习就能获得的，而是需要实践并且在实践中有意识、有目的地反思，这就是一种感悟[7]．

4.4 内涵认识的3个维度

以上3种学说围绕着对“感”的理解而展开，各有所侧重．“态度意识说”侧重于经过数学学习而形成对“数（或数学）”的主观态度，是一种数学方面的自觉意识或思维习惯（或心理倾向）．“直觉能力说”侧重于数的先天直觉，是一种无意识、非逻辑的直觉能力．“活动感悟说”侧重于数学活动后的“感悟”，是一种对数学活动有意识、有目的的归纳反思．虽然修订后用感悟对数感作表述，但数感的内涵不仅是“活动感悟说”的内容，而是3种学说的融合．

首先，对“数量和数量关系”的感悟是侧重于“物体个数多少”的直观判断，属于人的“直觉能力”，是数感的基础．其次，“感悟”既是行为动词（指感受的过程），也是结果名词（指领悟的结果）．例如，对一幅画的“看”“观”是感的过程，欣赏之后的“美的感受、情感的升华”是悟的结果．所以，“感悟”既指对“数学对象”和“数学活动”体会、体验的过程，也是指对“数学对象”和“数学活动”所蕴含的道理（思想方法）“悟”到的结果．最后，“悟”是有意识、有目的的反思归纳，可以使人的认识从特殊上升到一般，有助于形成更高层次的“数学态度意识”，是数感培养的目标．因此，可从3个维度认识数感的内涵：“直觉能力”为基础，“活动感悟”为过程，形成数学“态度意识”为目标（见图2）．

图2 数感内涵认识的3个维度

5 数感培养的两个方面

数感是关于“数与数量及数量关系、运算结果估计等方面”的感悟．对“数与数量”的认识必然涉及到“数量关系”，因此，可结合数感内涵认识的3个维度，从“数与数量及数量关系”和“运算结果估计”两方面探讨数感的培养．

5.1 数与数量及数量关系

如前所述，人类有觉察小数量物体变化的本能，这是进行“数与数量及数量关系”学习的基础．绝大多数的数概念可以从现实生活中找到模型，如自然数产生于数数，分数可看作整体与部分的关系，负数的意义可解释为“亏损”“零下”“逆向”或者“相反”；无理数可以看作是不可公约的量；复数则可以用于平面定位[22]．“数与数量及数量关系”的教学往往借助情境和活动，建立现实模型和数字的联系．例如，如果只是指着数字符号“4”对学生说“4”，然后跟读，这样建立的只是符号和读音的关系；如果只是指着数字符号“4”对学生说“4字像红旗”，然后学生练习书写，这样建立的只是符号和图形形状的关系；而将4个苹果、4支铅笔和4本书让孩子看、数，再认识数字符号“4”，这样建立的是现实数量与数字符号的关系．

对数的理解始于对现实物体数量的抽象，但作为独立的、可操作的思维对象，必然经过这样的逐级抽象：对物体的数量直觉→基于实物的数字抽象→脱离实物的数字抽象→基于数量关系的符号抽象．在逐级的抽象过程中，也完成对数符号、数意义、数表示、数关系的认识与理解．而对数与数量、数的认识、数的意义、数的表示这一系列定义的本质其实就是达成建立抽象的数和现实中的数量之间的关系的目的[23]．那么，通过逐级抽象对“数与数量及数量关系”的感悟更为核心的目标是建立数学与现实世界的关系，也即是用数学的眼光观察世界、用数学的思维分析世界、用数学的语言表达实现世界．从基础、过程、目标3个维度对《课程标准》中“数与数量及数量关系”内容及要求整理成表2．

5.2 运算结果的估计

沈威等认为[24]，数学估计是主体结合实际情境运用已有的数学经验产生一个相对快速且满足一定条件的数学判断的心理加工过程，从产生的结果角度将数学估计分为定量估计和定性估计；定量估计是获得一个量的判断，包括估数（与数字、数量大小判断有关）、估算（与数学计算有关）、估测（与长度、面积、重量、温度和价格等有关）3种；定性估计是获得一个猜想、思路或方法等非量的判断；定性估计有3个表现：猜想、对解题模式或解题方法的估计、统计估计．估算涉及理解数字大小、小数与分数系统、修正调整数字的能力．而这些能力均包含在数意识的几项特征中，因此，估算与数意识密切相关[22]．综上所述，数感所说的对“运算结果估计等方面”的感悟，应侧重于估算．

吴增生等认为[25]，人脑有两个数学认知加工系统，一个是估算系统，另一个是精算系统．而精算系统和估算系统又是基于语言符号，由人的客体归档系统和数量模拟系统进化而来．数量模拟系统是基于比率的客体运动、位置、距离、形状、大小等空间信息数量化加工能力；估算指在一些估算策略的基础上，通过观察、比较、判断、推理等认知过程，获得一种概略化结果．那么，在估算能力的培养过程中，就要以人类的数量模拟系统为基础，从学生最熟悉的身边事物出发，获得关于运动、位置、距离、形状、大小等方面估算经验和估算策略．

《课程标准》中“对大数的估计”就分两学段进行：第一学段是在“生活情境”中感受大数的意义，与之对应的是例3[15]：1 200张纸大约有多厚？你的1 200步大约有多长？1 200名学生站成做广播操的队形需要多大的场地？第二学段是结合“现实情境”感受大数的意义，与之对应的是例23[15]：如果一个人的寿命是76岁，这个人一生的心跳大约有多少次？光速大约是30万千米/秒，光从太阳到达地球大约需要多长时间？如果把100万张纸叠加起来，会有珠穆朗玛峰那么高吗？第一学段的生活情境：厚度可见的纸张、长度可测步长、位置距离可感的列队，为进行估算心理操作提供生活情境以及经验性策略．第二学段的估算虽有现实背景，但需要进行复杂的认知心理操作．沈威等研究了《课程标准》对数学估计能力培养的重点与规律[24]：第一学段的培养重点是定量估计的估测和估算；第二学段，要以定量估计为主，以定性估计为辅；第三学段，定量估计和定性估计并重．

估算课程内容在《课程标准（实验版）》和《课程标准》中的确定和保持，标志着对估算教育价值的认可．但在估算教学和学习过程中存在着为“估算”而“估算”的现象，具体表现是：为什么学估算？学估算有什么用处？在什么情况下用精算、什么情况下用估算[26]？这其实是估算教学目标的迷失与错位．估算得到的是概略化结果，在只有标准答案的考试体制下无法体现与评估，仍沿用与精算同样的目标则无所适从；但估算能力却影响生活的方方面面，小的方面如个人的生活起居，如由路程的估算而确定出发时间；大的方面如国家政策方针的制定，如对国家人口数量变化的预测而制定二孩政策．所以，对估算教学的目标取向是逐步积累估算经验，掌握常用的估算方法，丰富估算策略库，养成良好的估算意识．毕竟日常生活中经常遇到的是估算而不是精确的计算，估算可以使数字与真实生活情境联结起来，不至于使数字失去意义[26]．

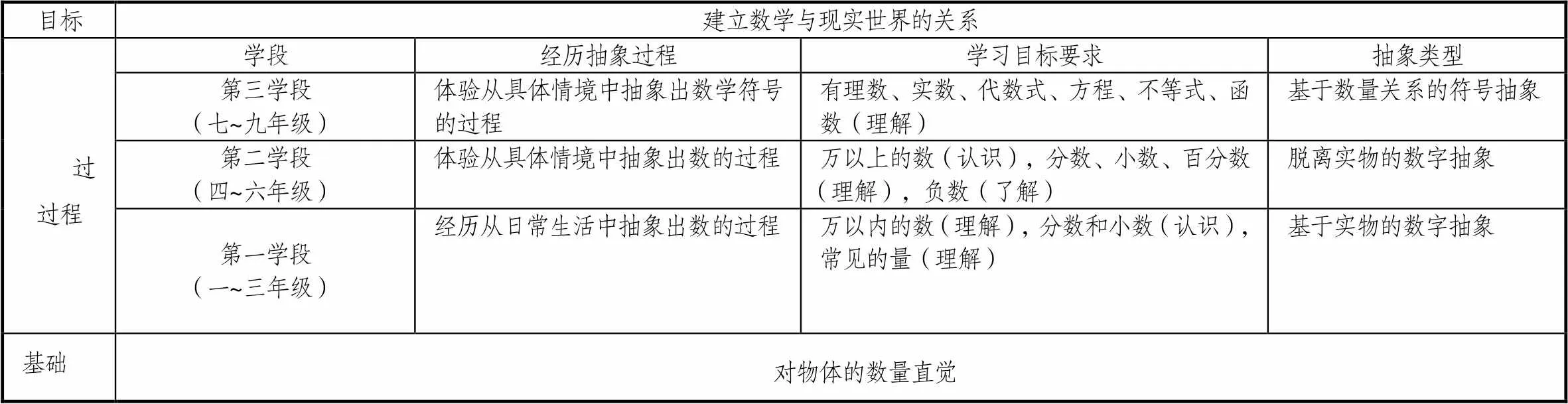
表2 “数与数量及数量关系”的3个维度

6 结语

从“双基”出发的中国数学教育始终在发展之路上，逐渐形成有中国特色的数学教育．有特色，是因为中国数学教育承载着落实“立德树人”根本任务、发展素质教育的功能；有特色，是因为中国数学教育勇于架起传统与发展之间的桥梁[27-46]．数感从提出至今将近二十年，仍然在路上，回顾数感的变化历程，重新审视数感的内涵，架起传统与发展之间的桥梁，使对数感的认识从“了解”到“理解”，为教学中自觉地“运用”奠定基础．

[1] 马云鹏，史炳星．认识数感与发展数感[J]．数学教育学报，2002，11（2）：46-49．

[2] 郑毓信．“数感”“符号感”与其它——《课程标准》大家谈[J]．数学教育学报，2002，11（3）：30-32．

[3] 何小亚．全日制义务教育阶段数学课程标准（实验稿）刍议[J]．数学教育学报，2003，12（2）：45-49．

[4] 叶蓓蓓．对数感的再认识与思考[J]．数学教育学报，2004，13（2）：34-36．

[5] 藤发祥．数感及其教育价值[J]．课程·教材·教法，2004，24（12）：47-50．

[6] 詹国梁．数感的特性[J]．苏州教育学院学报，2005（4）：78-78．

[7] 史宁中，吕世虎．对数感及其教学的思考[J]．数学教育学报，2006，15（2）：9-11．

[8] 徐文彬，喻平．“数感”及其形成与发展[J]．数学教育学报，2007，16（2）：8-11．

[9] 郭民，史宁中．小学生数感发展规律与特征的实证研究及其启示[J]．数学教育学报，2011，20（1）：23-25．

[10] 缪素萍．数感：从“边缘”走向“中心”[J]．江苏教育，2014（10）：38-40．

[11] 中华人民共和国教育部．中小学幼儿园教师培训课程指导标准：义务教育数学学科教学[M]．北京：高等教育出版社，2019：4-5．

[12] Daniel B B. Making sense of number sense implications for children with mathematical disabilities [J]. Journal of Learning Disabilities, 2005 (38): 333-339.

[13] David A S．人脑如何学数学[M]．赵晖，徐继红，李小溪，等译．上海：上海教育出版社，2016：9．

[14] 中华人民共和国教育部．全日制义务教育数学课程标准（实验稿）[M]．北京：北京师范大学出版社，2001：2．

[15] 中华人民共和国教育部．义务教育数学课程标准（2011年版）[M]．北京：北京师范大学出版社，2012：5，75，86．

[16] 史宁中．基本概念与运算法则[M]．北京：高等教育出版社，2013：5．

[17] 崔允漷．指向学科核心素养的教学即让学科教育“回家”[J]．基础教育课程，2019（Z1）：5-9．

[18] 梁建宁．基础心理学[M]．北京：高等教育出版社，2006：49．

[19] 何小亚．追求数学素养达成的教学设计标准与案例[J]．中学数学研究，2019（2）：1-8．

[20] 周治金，赵晓川，刘昌．直觉研究述评[J]．心理科学进展，2005，13（6）：745-751．

[21] 赵思林，朱德全．试论数学直觉思维的培养策略[J]．数学教育学报，2010，19（1）：23-26．

[22] 鲍建生，周超．数学学习的心理基础与过程[M]．上海：上海教育出版社，2009：238．

[23] 马玲．小学生数感培养的策略研究[D]．海口：海南师范大学，2014：18．

[24] 沈威，曹广福．数学估计及中国数学课程标准对其的培养要求[J]．数学教育学报，2015，24（4）：33-39．

[25] 吴增生，李吉宝．数学教学中估算与精算相结合原理初探[J]．数学教育学报，2015，24（5）：78-83．

[26] 郑庆全．当前估算教学：存在问题与解决策略[J]．数学教育学报，2015，24（3）：96-101．

[27] 王建磐．历史视角下的数学素养：讲好我们自己的故事[J]．数学教育学报，2019，28（3）：1．

[28] 严卿，喻平．初中生逻辑推理能力的现状调查[J]．数学教育学报，2021，30（1）：49-53．

[29] 李杰民，廖运章．条件概率的本质及其教学建议[J]．数学教育学报，2021，30（1）：54-60．

[30] 邓海英，严卿，魏亚楠．数学情境问题解决错误分析与评价[J]．数学教育学报，2021，30（1）：61-67．

[31] 于然，赵世恩．深度学习的内涵与教学实践——以小学数学为例[J]．数学教育学报，2021，30（1）：68-73．

[32] 林洪新，王云鹏，郑淑杰．小学数学运算规则学习的样例—问题匹配形式[J]．数学教育学报，2021，30（1）：74-78．

[33] 李保臻，马登堂．基于小学生数学运算素养培育的课例比较研究——以“三位数乘两位数”的同课异构为例[J]．数学教育学报，2021，30（2）：8-13．

[34] 范会敏，陈旭远，张娟娟．基于精准框架的素养导向数学教学评估——以全国小学数学（人教版）核心素养示范课教学视频分析为例[J]．数学教育学报，2021，30（2）：20-25．

[35] 赵莉，王春英，史宁中．分数概念表述和分数除法运算的比较研究及其对教学的启示[J]．数学教育学报，2021，30（3）：46-51．

[36] 王光明，彭宇佳，李健．小学高年级学生数学学习非智力因素常模及其等级评价标准的建构与应用——以天津市为例[J]．数学教育学报，2021，30（3）：52-58．

[37] 章全武．中国小学数学教材建设70年：回顾与展望[J]．数学教育学报，2021，30（3）：59-63．

[38] 丁锐，卫冰倩，RON TZUR，等．分数度量意义发展的认知根基及轨迹：分数图式进阶理论[J]．数学教育学报，2021，30（3）：64-72．

[39] 李晓东，蔡梦婕，江荣焕．克服比例推理的过度使用——抑制控制与工作记忆的视角[J]．数学教育学报，2021，30（3）：73-77．

[40] 伍春兰．PDSA视域下基于教师学习的中学数学课例研修研究[J]．数学教育学报，2021，30（3）：78-82．

[41] 栗小妮，汪晓勤．HPM课例研究对教师MKT的影响[J]．数学教育学报，2021，30（3）：83-89．

[42] 郑毓信．新一代数学教育研究者的成长[J]．数学教育学报，2020，29（6）：1-6．

[43] 邵贵明，胡典顺，柳福祥．论数学核心素养在高中数学课堂落地生根——以人教版高中“对数”教学为例[J]．数学教育学报，2020，29（6）：46-50．

[44] 郑庆全，周友士．透析数学课堂教学：“评价原理”的“认识”“应用”与“启示”[J]．数学教育学报，2020，29（6）：51-55．

[45] 王钦敏，余明芳．数学思维素养深度涵育：教学的进路与方略[J]．数学教育学报，2020，29（6）：56-60．

[46] 唐海军，高晶．初中数学教科书中历史名题分布特征及启示[J]．数学教育学报，2020，29（5）：8-13．

Revisiting the Meaning of Number Sense

LIN Sheng-wei

(Huazhou Xin’an Middle School, Guangdong Maoming 525133, China)

Due to an overlap in viewpoints, the perception of number sense is blurred. The introduction to the revision of number sense reflects the transformation process of the value orientation of Chinese education from the knowledge idea to the ability idea and then to the quality idea. Through a review of various views, we can understand the connotation of number sense according to three dimensions: intuition as the basis, activity perception as the process, and attitude awareness as the goal. The cultivation of number sense can be carried out from two angles: “number and quantity, quantity relationship” and “estimate of calculation result”.

number sense; number sense connotation; cognitive dimension; number sense cultivation

G633.6

A

1004–9894（2021）06–0069–05

林胜威．数感的修订变化与内涵认识[J]．数学教育学报，2021，30（6）：69-73．

2021–08–13

广东省教育科学规划2021年度中小学教师教育科研能力提升计划项目——初中数学核心素养培养的策略研究（2021YQJK357）

林胜威（1981—），男，广东化州人，高级教师，主要从事数学教育研究．

[责任编校：陈隽、陈汉君]