七年级数学教材中的推理与证明

付 钰，王嘉瑶，綦春霞

七年级数学教材中的推理与证明

付 钰，王嘉瑶，綦春霞

（北京师范大学 教育学部，北京 100875）

应用斯蒂利亚尼德斯的推理与证明分析框架，分析人教版、北师版、北京版3个版本七年级教材中的推理与证明．研究发现：七年级教材中的推理与证明任务较少，其中，数与代数内容领域中包含的任务最多，其次是图形与几何、统计与概率内容领域；进而分析推理与证明的子活动的设计意图，发现大多数确定的模式没有促进形成猜想，大多数猜想没有促进证明．研究结果对中国教材研究具有一定的启示，不同版本教材中各内容领域均存在推理与证明；数学教材编排的特点是螺旋上升；教师应注重教学过程中给予学生推理与证明的机会．

数学教材；七年级；推理与证明

2001年6月，教育部颁布了《中小学教材编写审定管理暂行办法》，从教科书编写的资格和条件、立项和核准、初审与实验、教科书审定等方面做出了详细规定．自此，新的“一纲多本”管理体制初步形成．“一纲多本”的成效与教材研究的进展密切相关[1]．2020年1月，教育部印发了《中小学教材管理办法》，明确要求“注重教材的系统性，结构设计合理，不同学段内容衔接贯通，各学科内容协调配合”[2]．教材在学习和教学过程中起着非常重要的作用，被视为预期课程与应用课程之间的中介[3]．在过去的几十年里，世界各地越来越多的研究者开始关注数学教材研究[4-5]

1 研究背景

数学证明是数学学科的特征，是数学活动的重要组成部分．从证明结果的呈现方式来看，它是由一系列有逻辑关系的数学语句组成的；从数学家发现数学命题、获得证明方法的过程来看，一般包括探索数学关系和规律、概括规律的一般形式并形成猜想、检验和修改猜想、提供猜想成立的非形式化的论证等内容．这些过程有助于数学家理解数学关系，获得最后的形式化证明[6]．学生学习证明不能忽视这些过程．推理和证明是一个复合词，它描述一个总体活动，包括4个子活动：识别模式，形成猜想，提供证明论证、非证明论证．

推理和证明是学生数学学习的难点，也是数学教育研究者青睐的研究对象．数学教学是教师、学生、数学内容3者之间的交互过程，数学教育研究聚焦的是其中的一个或几个方面．数学教材是提供数学内容的重要载体，它决定课堂中学生的学习内容，是影响学生学习质量的因素之一．为了解数学教材提供给学生推理与证明的学习机会，这里对中国不同版本七年级数学教材进行分析，旨在为完善不同版本初中教材提供重要的参考，同时为使用不同版本教材的一线教师提供教学依据．

2 研究设计

2.1 研究内容

选取2012年人民教育出版社出版的（简称“人教版”）、2014年北京师范大学出版社出版的（简称“北师版”）、2013年北京出版社出版的（简称“北京版”）七年级教材中的内容进行分析，具体内容见表1所示．

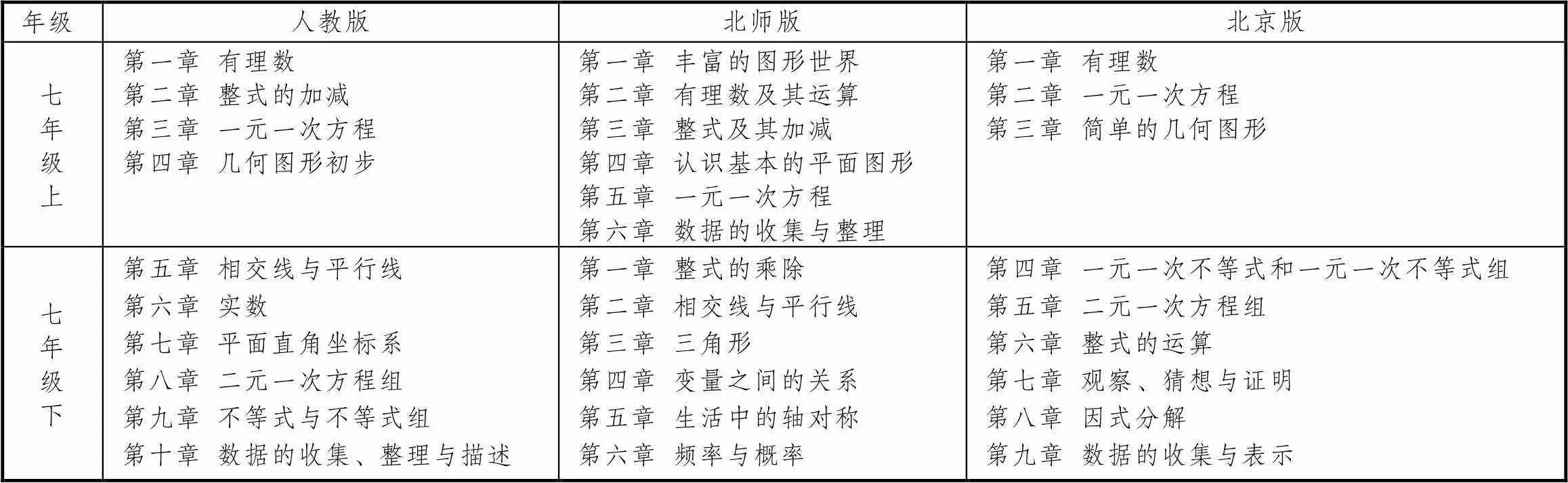
表1 所选取的3个版本教材的研究内容

2.2 研究框架

研究采用斯蒂利亚尼德斯（Stylianides）的推理与证明分析框架[7]，框架分为维度一与维度二，维度一分为识别模式，形成猜想以及提供证明论证、非证明论证；维度二分为模式、猜想、证明论证的目的，分析框架如表2所示．

表2 推理与证明的分析框架

3个版本数学教材包含了不同的栏目，如数学活动、课题学习等，分析内容缺乏一致性．为了使研究结果具有可比性，研究者选取了3套数学教材的正文部分，并对正文部分的推理与证明任务进行了分析[8]．研究者以教师用书中出现的习题分析作为辅助材料确定正文部分的任务划分．在这项研究中，任务作为分析的单位，被分析的任务会被编码为表2所示的推理与证明的子活动．

在表2中，推理与证明涉及2个大类、4个子类，2个大类指的是数学一般化和为数学命题的成立提供依据，数学一般化包括识别模式和形成猜想，为数学命题提供依据包括提供证明论证和非证明论证．

模式指的是给定对象的数学关系，根据刻画对象的模式是否唯一分为合理的模式和确定的模式，前者模式是不唯一的，后者模式是唯一的．在明确的模式中，模式具有确凿的证据，而在合理的模式中，模式不具备确凿的证据．

猜想指的是对数学关系作出的不能完全确定其正确性的合理的假设．研究者在研究中修正了斯蒂利亚尼德斯（Stylianides）关于猜想的框架，在猜想中加入了对猜想的检验和对猜想的发展[9-10]．形成猜想和识别模式都属于数学一般化的活动，其主要区别是猜想得到的数学关系包含个体的不确定性，其正确性是需要证明的，而通过识别模式获得的数学关系不包含个体的不确定性．

数学证明是以一些基本概念和基本假设为前提，通过合乎逻辑的推理得到结论的过程．分为两个子类，第一个是类属性证明，即以一个具体的例子作为代表表述整个证明过程的证明；第二个是非类属性数学证明，如反证法、数学归纳法、穷举法等．

非数学证明论证即对命题的正确性给出合理的解释，不是严格的数学证明，分成经验性说理和合理解释两个子类．经验性说理指的是用举例子的方法证明一般性的命题，缺少基于数学定义、定理的推理．合理解释是对命题的正确性给出合理的解释，但推理的过程不严密，缺少了必要的步骤．例如，用折叠重合的方式说明两个三角形全等属于合理解释，而用三角形的全等条件来说明则属于数学证明．

维度二是对维度一的补充，分析识别模式、形成猜想、证明论证的作用可以揭示教材是否提供给学生理解3者联系的学习机会．例如，在数学中，模式、猜想和证明之间的一个重要联系是模式可以产生猜想，而这反过来又可以促进证明的发展（Polya，1954）．证明可以用于多个目的：解释、验证、证伪和产生新知识等．

2.3 部分题目编码示例

2.3.1 单一编码示例

例1 如图1，由于题目中的要求是“设未知数列出方程”，由题意可知，正方形的边长与24 cm的铁丝之间的关系是确定的，并且列出方程后无其它推理与证明活动，故其维度一的编码为明确的模式，维度二的编码为不促进猜想．

图1 选自人教版七年级上P79

例2 如图2，由于题目中的要求是“观察下面的点阵图和相应的等式，做出猜想”，并且根据题意，学生猜想之后需要列出第行点阵图相对应的等式，不涉及证明的活动，故其维度一的编码为发展猜想，维度二的编码为不促进证明．

图2 选自北京版七年级下P121

例3 如图3，由于需要说明与平行的理由，要求学生给出理由即严谨的证明，故其维度一的编码为提供证明论证中非类属性数学证明，维度二的编码为验证．

图3 选自北师版七年级下P54

例4 如图4，由于题目中要求学生观察算式及其运算结果，阐述发现并举例验证．学生只需对算式的正确性给出合理的解释并举例，无需严谨的证明过程，故其维度一的编码为提供非证明论证．

图4 选自北师版七年级下P20

2.3.2 多重编码示例

编码包括以下环节：①确定提供推理和证明学习机会的任务，它们至少包含分析框架维度一中的4个活动中的一个；②根据分析框架中的维度一的推理与证明的子活动进行维度二的编码．如图5所示，学生需要猜想两个图形的面积之后，对自己猜测进行验证．故其维度一的编码为发展猜想、提供证明论证（非类属性证明），维度二的编码为发展猜想的目的即促进证明，提供证明论证的目的是验证猜想．

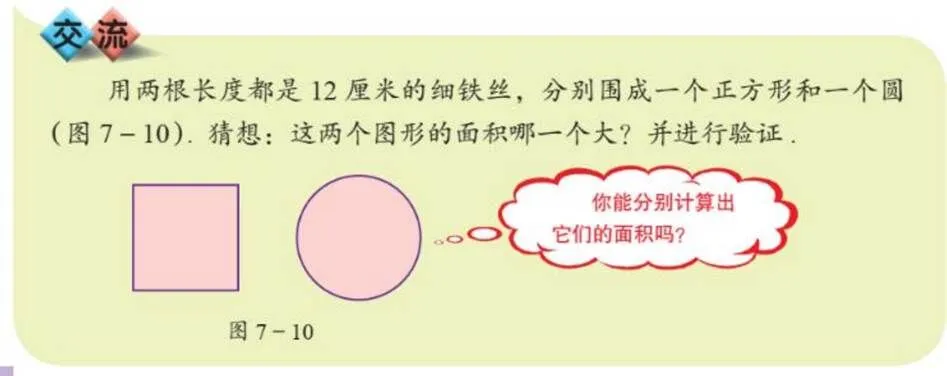
图5 北京版七年级下P120

3 研究结果与分析

3.1 总体情况

为了呈现3个版本七年级教材中推理与证明任务的情况，研究者将任务、推理与证明任务、推理与证明任务百分比整理如表3所示．

由于3个版本教材的任务数量不同，难以比较推理与证明任务的数量，故在研究中使用百分比来衡量3个版本中推理与证明任务的多少．由表3可知，在七年级教材中，北京版教材包含的任务最多，高于北师版、人教版教材的任务数量，但人教版的推理与证明任务的百分比高于北京版、北师版教材．同时3个版本七年级教材中推理与证明的任务百分比均低于30%．由于七年级是小学阶段与中学阶段的衔接，学生需面临学习科目增加、学习内容也明显加深等问题，故应重视小学阶段与中学阶段的衔接问题．为了使学生更好地过渡，七年级教材中推理与证明任务不宜过多，而应在八九年级呈现逐渐增长的趋势．

表3 推理与证明任务的总体情况

3.2 子活动的分布情况

推理与证明子活动在3个版本教材分布的百分比，如表4所示．

表4 推理与证明子活动的分布情况

由表4可知，3个版本七年级教材中推理与证明的子活动提供非证明论证的占比最多，提供证明论证的占比最少．同时，3个版本教材呈现了细微差异，如人教版七年级教材推理与证明的子活动识别模式的占比高于形成猜想的占比，北师版和北京版则相反．同时，北师版中提供证明论证的百分比明显高于人教版、北京版．由于3个版本教材的编写顺序不同，研究者在表1呈现了研究内容，北师版教材将三角形安排七年级下教学，导致北师版教材提供证明论证的百分比明显高于人教版、北京版．

3.3 各内容领域分布情况

《义务教育数学课程标准（2011年版）》（以下称《标准》）教材编写建议中提出，无论是“数与代数”“图形与几何”还是“统计与概率”的内容编排中，都要尽可能地为学生提供观察、操作、归纳、类比、猜测、证明的机会，发展学生的推理能力[11]．3个版本推理与证明任务在个内容领域分布的情况，如表5所示．

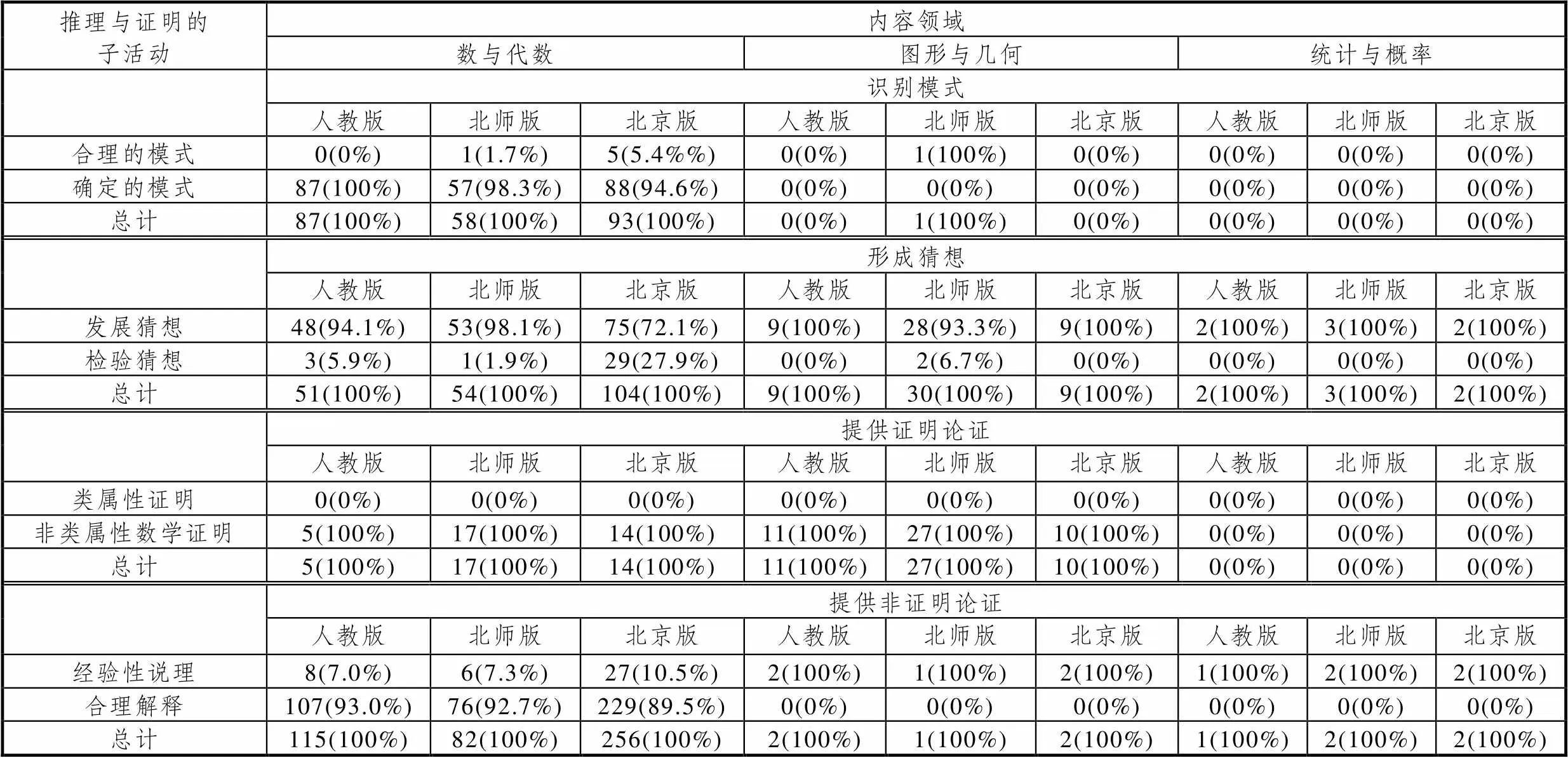
表5 推理与证明任务在各内容领域分布情况

由表5可知，七年级数学教材中，推理与证明任务在各内容领域分布存在较大差异．数与代数内容领域包含的推理与证明任务最多，其次是图形与几何、统计与概率内容领域．数与代数内容领域是七年级教材的重心，七年级并未设置过多的图形与几何、统计与概率内容．同时，在数与代数内容领域中，教材为学生提供非证明论证的机会最多；在图形与几何内容领域中，教材为学生提供形成猜想、提供证明论证的机会较多．

此外，3个版本七年级教材为学生提供的推理与证明的子活动分布也略有不同．具体而言，人教版七年级教材数与代数内容领域中，教材为学生提供的识别模式的机会也较多，其次是形成猜想的机会；北师版七年级教材在图形与几何内容领域中，教材为学生提供的证明论证的机会明显高于其它两个版本；北京版七年级教材数与代数内容领域中，教材为学生提供的形成猜想的机会明显高于识别模式的机会．

3.4 推理与证明中“模式”“猜想”“证明论证”的目的

分析识别模式、形成猜想、证明论证的目的可以揭示教材是否提供给学生理解三者联系的学习机会．由于七年级教材中合理的模式数量较少，故本研究只分析确定的模式．图6-8分析结果表明：3个版本教材中，大多数确定的模式没有促进形成猜想，大多数猜想没有促进证明．故教师在使用教材时，要妥善设计教学活动，为学生提供足够的思考空间．

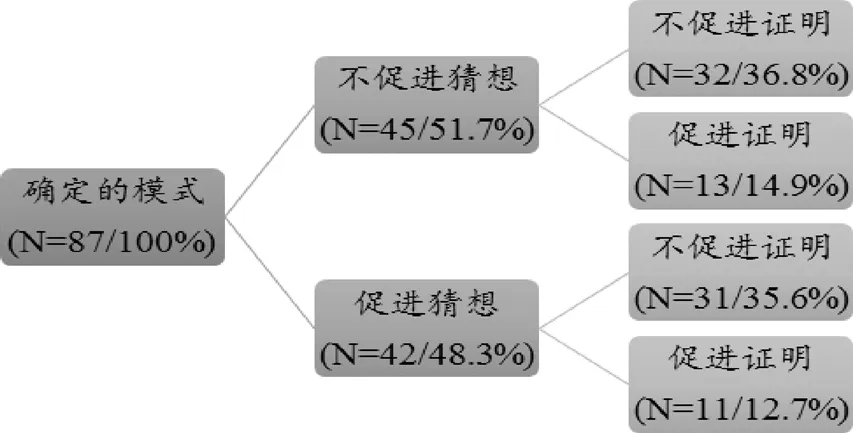
图6 人教版教材七年级推理与证明中模式与猜想的目的

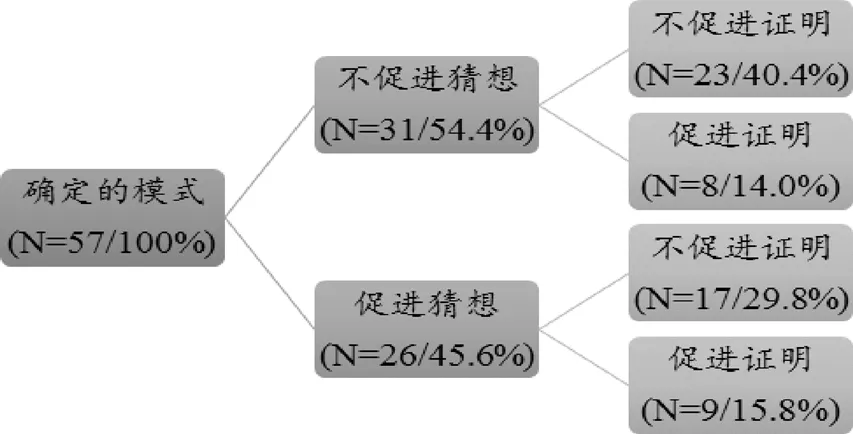
图7 北师版教材七年级推理与证明中模式与猜想的目的

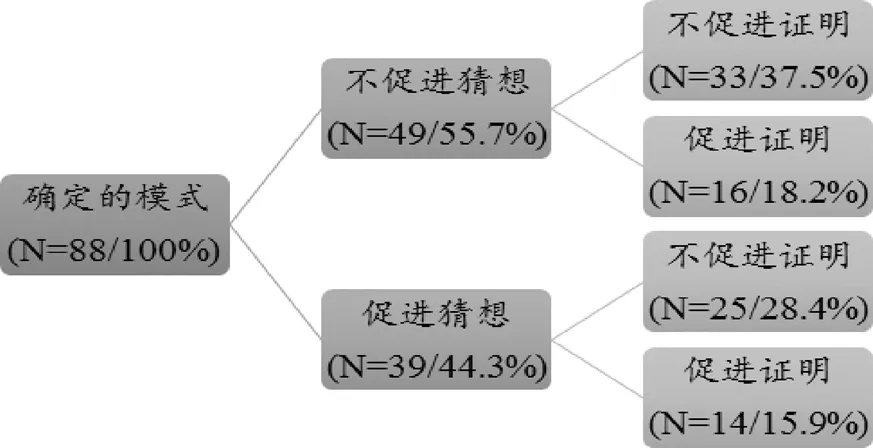
图8 北京版教材七年级推理与证明中模式与猜想的目的

由于研究中类属性证明的任务较少，研究者考查的是非类属性数学证明的目的．由表6可知，所分析的推理与证明的任务中非类属性数学证明的目的存在多样性．在人教版和北京版教材中，产生新知识占比最高，其次是解释、验证．北师版教材中，验证占比最高，其次是产生新知识、解释、证伪．而在人教版、北京版教材中，非类属性数学证明没有体现证伪的目的．此外，许多学生不能区分诸如解释、论证、验证和证明这些不同数学推理之间的区别[12]．

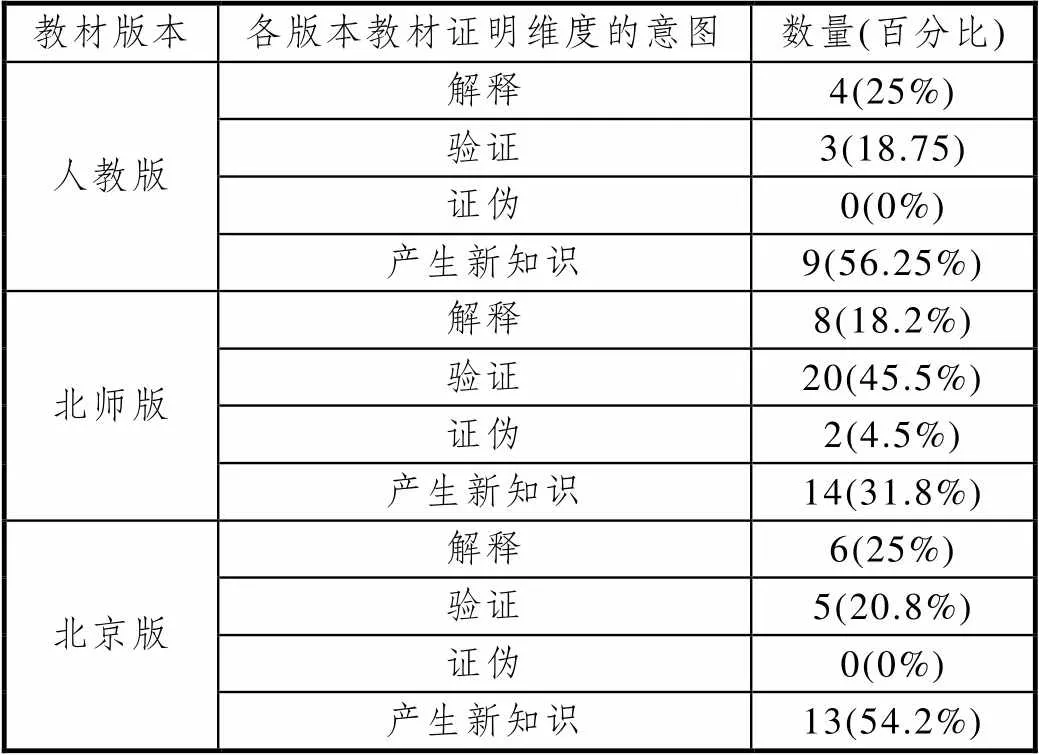
表6 推理与证明任务中非类属性数学证明的目的

4 研究结论与启示

4.1 不同版本教材中各内容领域均存在推理与证明

研究结果表明，不同版本教材中各内容领域均存在推理与证明，其中，数与代数内容领域明显高于其它两个内容领域．这与“《标准》对数与代数知识领域的关注的重点已经不再仅仅是运算—数值计算、代数运算、求解方程（不等式）等，更多的是将代数作为表示、交流与解决问题的工具”的理念是一致的[13]．从总体上看，七年级数学教材的编写是基本符合《标准》要求的．此外，3个版本七年级教材中推理与证明的子活动提供非证明论证的占比最多，提供证明论证的占比最少．正如斯蒂利亚尼德斯指出，证明论证要求学生提供严谨的证明．他进一步发现，学生对证明的误解与教材中出现的特定推理与证明类型的频率之间几乎没有关联．尽管在教材中很少有证明论证的机会，但是学生们却更倾向于依靠举例来证明数学命题的正确性．教材中证明论证的百分比不是学生对证明产生误解的主要原因，但它在帮助学生做出更严谨的证明方面有积极作用，因此建议编写者深入思考未来在教材编写中增加证明论证比重的可行性．

4.2 螺旋上升是数学教材编排的特点

斯蒂利亚尼德斯指出，非证明论证应在各年级减少，而证明论证则应随着年级增长而增加，这与中国教材编排的特点相契合．由于考虑学生的认知特点以及教材编排特点，七年级学生在理解过多地抽象的几何证明上存在困难，同时，中学阶段统计与概率内容课时较少，并且要螺旋式（教材在呈现相应的数学内容与思想方法时，应根据学生的年龄特征与知识积累，在遵循科学性的前提下，遵循逐级递进、螺旋上升的原则．螺旋上升是指在深度、广度等方面都要有实质性的变化，即体现出明显的阶段性要求）地安排在七至九年级．因此七年级数学教学的重点放在数与代数领域．另外，数与代数领域中出现的推理与证明大多是三段论简化后的应用，这与几何等领域中涉及到的推理方法相比是较为简单的，往往不需要对知识点和方法的灵活选择，而是有固定的步骤，例如求解一元一次方程，其步骤具有固定性，每一步的推理过程也相对有更加充足严谨的理由支撑．

4.3 教师应注重教学过程中给予学生推理与证明的机会

范良火教授曾指出，教材是学生进行数学学习的主要来源．学生喜欢自己直接阅读教材，这既是教师的要求，也是学习动机的驱使．学生的数学学习不仅通过阅读教材，而且通过课堂教学中教师将大部分问题转化为自己的教学实践．结果表明，3个版本教材中，大多数确定的模式没有促进形成猜想，大多数猜想没有促进证明，这与戴维斯（Davis）的研究结果一致[9]．因此，研究者们担心如果教师不习惯按照教材讲授每个课时的内容可能会错过数学教材中一些潜在的推理与证明机会[14-15]．这一现象可能会导致学生拥有有限的推理与证明机会．所以一方面，教材要给予学生充分的推理与证明机会，例如在探索有理数减法法则时，可以先呈现减数是正数的特例，进而在与加上减数的相反数的运算结果进行比较，最后探究减数是负数的特例，这样是从学生的已知出发探究新知的过程，也是引导学生思考、总结有理数减法法则的全过程；另一方面，教师要妥善设计教学活动，为学生提供足够的思考空间，例如在探索有理数加法法则时，教师应注重学生从特例出发，分类总结同号、异号、一个数同零相加的3种情况，让学生经历观察、猜想、归纳的过程，为学生提供充分的推理与证明机会．

此外，在每一年级的数学教材中安排证明和非证明论证的机会在多大程度上对学生的数学学习最为合理，需要进一步研究．总之，在教材改进过程中，各版本教材应做到既保留自身鲜明的特色，又能努力贴合《标准》对学生能力培养的要求，这样才能更好地为一线教师的教学提供内容素材与教学资源．

[1] 钟启泉．一纲多本：教育民主的诉求——我国教科书政策述评[J]．教育发展研究，2009，29（4）：1–6．

[2] 中华人民共和国教育部．教育部关于印发《中小学教材管理办法》《职业院校教材管理办法》和《普通高等学校教材管理办法》的通知[EB/OL]．（2019–12–19）[2020–12–20]．http://www.moe.gov.cn/srcsite/A26/moe_714/202001/t20200107_414578.html．

[3] SCHMIDT W H, MCKNIGHT C, RAIZEN S. A splintered vision: An investigation of U.S. science and mathematics education [J]. Wisconsin Teacher of Mathematics, 1997, 48 (2): 4–9.

[4] FAN L, ZHU Y, MIAO Z. Textbook research in mathematics education: Development status and directions [J]. ZDM, 2013, 45 (5): 633–646.

[5] FAN L, XIONG B, ZHAO D, et al. How is cultural influence manifested in the formation of mathematics textbooks? A comparative case study of resource book series between Shanghai and England [J]. ZDM, 2018, 50 (5): 787–799.

[6] 鲍建生，徐斌艳．数学教育研究导引（二）[M]．南京：江苏教育出版社，2013：267–272．

[7] STYLIANIDES G J. Reasoning-and-proving in school mathematics textbooks [J]. Mathematical Thinking and Learning, 2009, 11 (4): 258–288.

[8] ZHANG D, QI C. Reasoning and proof in eighth-grade mathematics textbooks in China [J]. International Journal of Educational Research, 2019 (98): 77–90.

[9] DAVIS J D, SMITH D O, ROY A R, et al. Reasoning-and-proving in algebra: The case of two reform-oriented U.S. textbooks [J]. International Journal of Educational Research, 2014 (64): 92–106.

[10] FUJITA T, JONES K. Reasoning-and-proving in geometry in school mathematics textbooks in Japan [J]. International Journal of Educational Research, 2014 (64): 81–91.

[11] 中华人民共和国教育部．义务教育数学课程标准（2011年版）[M]．北京：北京师范大学出版社，2012：57．

[12] DREYFUS T. Why Johnny can’t prove [J]. Educational Studies in Mathematics, 1999, 38 (1): 85–109.

[13] 马复．认识新课程意义下的数学教材[J]．数学教育学报，2005，14（1）：49–51．

[14] BALL D L, COHEN D K. The role of curriculum materials in teacher learning and instructional reform [J]. Educational Researcher, 1996, 25 (9): 6–14.

[15] TARR J E, CHÁVEZ Ó, REYS R E, et al. From the written to the enacted curricula: The intermediary role of middle school mathematics teachers in shaping students’ opportunity to learn [J]. School Science and Mathematics, 2006, 106 (4): 191–201.

Reasoning and Proof in Seventh-Grade Mathematics Textbooks

FU Yu, WANG Jia-yao, QI Chun-xia

(Beijing Normal University, Faculty of Education, Beijing 100875, China)

The reasoning and proof framework of Stylianides was applied to explore reasoning and proof in seventh-grade mathematics textbooks. The results show that there are fewer reasoning and proof tasks in the seventh-grade textbooks; Number and Algebra contains the most reasoning and proof tasks, followed by Graph and Geometry, Statistics, and Probability. In addition, the purposes of the reasoning and proof subactivities were analyzed. It was found that most of the definite patterns do not promote the conjectures, and most of the conjectures do not promote the proofs. This provides a unique insight for research on mathematics textbooks in China. There are reasoning and proof tasks in various content areas in different versions of mathematics textbooks. The arrangement of the mathematics textbooks is characterized by a spiral rise. Teachers should pay attention to giving students reasoning and proof opportunities during the teaching process.

mathematics textbooks; Grade 7; reasoning and proof

G633.6

A

1004–9894（2021）06–0064–05

付钰，王嘉瑶，綦春霞．七年级数学教材中的推理与证明[J]．数学教育学报，2021，30（6）：64-68．

2021–08–02

北京市教育科学“十三五”规划重点课题——指向育人价值的高中数学概念教学研究（CDAA2020053）

付钰（1994—），女，黑龙江绥化人，博士生，主要从事教材比较、教学评价研究．綦春霞为本文通讯作者．

[责任编校：陈隽、陈汉君]