因生而异 因地制宜——大单元视角下“凑十法”教学的实践探索

文|金 滢 龚斌斌

一、“移植”之困：“十”之欲出，“凑”而不得

在一次单元整合教学的省级研讨活动中，笔者偶遇别开生面的“凑十法”，心生向往，于是“移植”进自家课堂。奈何过程和结果却与活动中的课堂大相径庭，不如人意。

1.结果式表征抑制算理的生长。

关于“9+4”，学生选取小棒、画图和算式表征的典型进行交流、对比，但学生对“凑十”并没有特别鲜明的需求和倾向。

2.模仿式迁移违背整合的初衷。

通过“9+4”的学习，引导学生用“凑十法”迁移计算“8+4”和“7+4”，学生情况如下：

二、刨根寻因：“学”之所需，法亦有别

1.他们的起点≠我们的起点。

随着社会的发展，家长对于教育的期望和要求越来越高，但城乡结合地区的家长大多还停留在知识技能培养的层面，把机械记忆结果作为计算学习的重点，很少会引导学生思考“为什么”。因此，我们的学生在算理的学习起点上相对要低一些。

2.位值的理解≠运算的理解。

对于一年级学生而言，对位值的“十”和运算产生的“十”还没有很好地进行关联，因此，对于为什么要“凑十”是迷茫的。

3.画图的经验≠符号的经验。

学生对于计算算理的表达能力有所欠缺，对于如何利用图和式来表达自己的思考过程缺乏一定的经验基础，尤其是把图和式进行主动地转化更是难上加难。

三、“嫁接”修枝：纵览全局，整合有度

单元教学整合绝非只是简单地整合单元学习内容，整合的策略更不能简单地加以“移植”，必须在精确掌握学生的学习起点基础上，通过拓展、重构等策略，加工单元知识点，以促进学生理解算理，提高运算能力。

（一）铺垫：特殊的“十”运筹帷幄

1.“格点”为媒，联结数与运算。

10 以内数的认识，始终遵循的一条主线就是从“实物——横向计数器——点子图——抽象出数”，人教版在学习10 的加减法时，安排了这样的方式展开，充分体现了点子图在沟通算式和分合式之间的重要作用。其实，这是“凑十”的萌芽时刻，借这个起点，笔者又进一步设计了以下的“凑十”练习：

利用格子图进行凑十，对应呈现加减法算式。通过系统学习，让学生脑中有图式，构建起10 的数模型，为“凑十法”计算做好准备。

2.意义渲染，感悟重要价值。

构建起10 的数模型后，还应该让学生了解“十”的特殊性，比如借助教材的《你知道吗》和绘本《古人是怎样计数的》引领学生走进十进制的产生。在此基础上，让学生走进生活，去寻找生活中特殊的“10”，从数学回归生活的过程中，学生发现原来“10”真的很特殊、很重要。

3.图式转换，爱上“10 加几”。

“10 加几”是学习了20 以内数的认识，掌握了20以内数的组成的基础上进行学习的，它是将一个数“十几”转化为一个算式“10 加几”的符号化变形，小棒直观图架设起两者之间转换的桥梁。但我们的教学并不能止于此处，更重要的是，让学生经历在例题学习的基础上创造出10 加几的算式，同时通过有序思考、对比观察，发现“10 加几等于十几”这一重要规律，感受到计算的便捷，让学生爱上“10 加几”。

（二）构序：运算的“十”多边共识

?

1.切换慢镜头，“倒逼”算理丝丝入扣。

运算方法可以通过简单的模仿进行学习，而运算能力的形成则必须依赖对算理的理解。笔者试着将原设计里利用“9 加几”的计算教学来理解“凑十法”的过程改为“串联”的呈现方式，层层深入，逐层对比。让学生在整个方法优化和沟通的过程中，感受到“凑十”思维对进位加法计算的必要性。

（1）动态演绎，定格“跳跃式”思维。

美国学者富森将表内加法进行划分，不进位的是“单一单位概念结构”，进位的是“多单位概念结构”。对于后者，通过前测可以发现，学生有两种水平：转换为单一单位概念结构，也就是接着数；另一种就是转化成相对独立的两个单位，也就是直接“凑十”。因此，先借助半抽象的小棒来实现水平一到水平二过渡。

师：你知道9 加4 等于几吗？

师：看来大家都已经知道9 加4 的结果了，那么这个结果是怎么得来的呢？老师为大家准备了一些小棒，请大家借助小棒，摆一摆9 加4 得到13 的计算过程。

对比小结：第三种方法是先得到了10，再与3 合并得到13，我们一眼就看出来了。再通过关键问题“为什么只移动1 根”思考凑十的另一个核心要素。

（2）格点再现，唤醒“凑十”经验。

利用点子图解释让学生在头脑中主动唤起先前建立的10 的模型结构。

师：刚刚大家用小棒摆出了9 加4 等于13 的计算过程，如果用小圆圈来画一画，画出9 加4 等于13的计算过程，你们能做到吗？

对比小结：第三种方法，我们不但能看出是9 加4，还圈出了10，让我们一眼就看出13。

（3）符号表征，实现算理内化。

在直观积累的基础上，用算式进行表征，就是符号化表征的进阶学习，符号化的过程本就是抽象的过程，抽象水平越高，可迁移的可能性就越大。

师：老师如果要你们用写算式的方法，写出9 加4 等于13 的计算过程，你们还能做到吗？

对比小结：第三种方法我们不但看到了9 加1 得到10 的过程，我们还能清楚地看出1 是从4 里面分出来的，而且还剩下3，这样10 和3 相加就马上得到13 了。

最后通过让学生同桌交流，对9+4 的三次表征方法异中求同，引导学生发现，无论是小棒、点子图还是算式，都经历了从4 里面拿出1，和9 组成10，10 再与3 合并得到13，“凑十法”一词的出现水到渠成。

2.推进快镜头，迁移算理步步为营。

（1）似曾相识再凑十。

第二环节选择一个与9 接近的8 先进行迁移，就是要培养学生具备有意识“凑十”到自主迁移的能力，让学生在微妙的变化中，感受到同中有异、异中有同，跳出“把9 凑十”、“用1 凑十”的思维框架。

师：同学们，9+8 你们已经会算了，老师现在要将这个算式变一变，你还会吗？请你在《学习单》上记录你的计算过程与想法。

师：都是8+9=17，过程有什么不一样？

通过交流发现，8+2=10，从第二个加数中拿出几去凑十，要看另一个加数是多少。

（2）不同角度找本质。

同一道题既可以把前一个加数凑成十，也可以把后一个加数凑成十，通过对比可以加深算理，同时再次体会8 和9 凑十过程是不同的，为后面学习小数加大数时的灵活选择方法做准备。

师：这两种方法又有什么相同和不同的地方？

对比小结：我们不仅可以将第一个加数凑成10，还可以将第二个加数凑成10。不管怎么样，我们在计算这类加法时，都是先想“凑十”再计算的。

（3）触类旁通想转化。

6、5、4、3、2 加几的计算虽然也可以转化为10 加几，但加数与10 相差越来越大，“凑十”的过程也越来越复杂。因而，需要在枚举的基础上，让学生自主地联想到将小数加大数转化为大数加小数。

师：那么如果在计算中出现了7、6、5、4、3、2，也可以通过先凑“十”来计算吗？

要求：请你自己编两道结果是20 以内，计算过程中需要用到“凑十”想法的算式，并把你的计算过程清楚地记录下来。

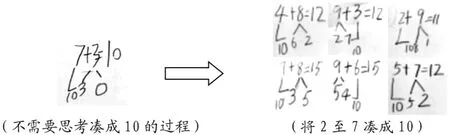
师：在计算的时候有什么相同的地方？

小结：当我们想好了要把其中一个加数凑成10，就只要想另一个加数需要分出几、还剩下几，这样就可以很快得到计算的过程和结果了。

师：为什么都是凑成十，而没有凑成其他数？（10加几最方便——凑十的意义完美流露）

师：这两位同学计算同一道算式，你更喜欢选择哪种方法？

小结：当我们遇到小数加大数时，可以联想大数加小数得到结果。

（三）融通：高阶的“十”细致深刻

数学学习的结构化有助于提高学生的学习能力，在教学时将相应的算式归类比较，有助于学生发现计算中的规律，将隐藏其中的算理进一步挖掘，在推理过程中进一步感悟凑十背后的秘密，提升计算的速度。

1.纵向勾连，归纳和演绎中整合运算。

师：结果是20 以内需要思考“凑十”的算式还有很多，老师将其中的一些整理在一张表格中。你能发现9 加几的算式有什么规律吗？得数有什么特点？得数和第二个加数有怎样的联系？

通过交流学生逐渐发现其中的规律：得数都是十几，得数个位上的数比第二个加数少1。

师：十几中的10 从哪儿来的？为什么每个得数的个位比第二个加数小1？

引导学生结合算理来分析，通过这样的有序列举、观察比较、分析归纳，学生概括出“凑十减一”的简化思考过程的方法，将分解的思维动作整合为算法模块，提高计算的速度和正确率。

2.横向勾连，类比和演绎中整合运算。

利用9 加几的规律，让学生进一步有序填写空格中的算式，并继续观察剩余的几列算式中蕴藏的规律。有序的学习素材能较好地提高学生的观察能力和分析能力，促进学生有效地展开探索活动。这里，既可以依次进行分析，也可以通过9 加几推理分析，并通过核心问题“为什么8 加几是凑十减二，7 加几是凑十减三”促使学生在类比推理的验证过程中回归“凑十法”的算理本质，提升运算能力，发展推理能力。