部分压扁热管等效导热模型特性研究

2021-12-07甘云华黄昭惠梁嘉林董道伟马力刘晋龙罗奇梁李勇

华南理工大学学报（自然科学版） 2021年10期

甘云华黄昭惠梁嘉林董道伟马力刘晋龙罗奇梁李勇

(1.华南理工大学电力学院，广东广州 510640；2.江西耐乐铜业有限公司，江西鹰潭 335211；3.华南理工大学机械与汽车工程学院，广东广州 510640)

热管[1-3]和均温板[4-6]在电子设备热管理领域[4,7]和新能源汽车热管理领域[8-9]得到广泛应用。而仿真模拟是研究基于热管的热管理系统的一个重要方法。在基于热管的热管理仿真中往往采用等效导热模型对热管进行简化。Zhang等[10]将扁平热管视为高导热系数的均匀固体导体。Behi等[11]通过等效热阻电路模型计算了L型压扁热管的总等效导热系数，将L形扁平热管视为均匀固体导体。Wang等[12]将部分扁平的热管设置为均匀的固体导体，并通过实验结果计算出总热管的等效导热系数。Liang等[13]在仿真模拟中把部分压扁的热管等效为各向异性导热系数固体导体，将压扁段和圆管段轴向热阻设定为圆管段蒸汽等效热阻，而将压扁段的厚度方向和圆管段的径向的热阻设定为管壁和吸液芯的热阻之和。但是这种方法需要进一步改进，因为压扁段与圆管段的蒸汽流动阻力不同，压扁段和圆管段应采用不同的等效导热系数。

因此，本研究在现有的热管等效导热模型的基础上进行改进，提出了适用于部分压扁热管的两种等效导热模型：分段各向异性等效导热模型和分层分段等效导热模型。在分段各向异性等效导热模型中，将热管分为压扁段、突扩段和圆管段，对压扁段和圆管段分别设置各向异性的等效导热系数。在分层分段等效导热模型中，将热管分为管壁层、吸液芯层和蒸汽层，同时将蒸汽层分为压扁段、突扩段和圆管段，分别设置各向同性的等效导热系数。另外本文还对热管工作温度和吸液芯等效导热系数对两个等效导热模型准确性的影响进行了研究，并从热阻等效电路模型的角度进行分析。

1 等效导热模型与吸液芯模型

1.1 部分压扁热管等效导热模型

1.1.1 分段各向异性模型

与圆管热管或完全扁平的热管不同，部分压扁热管不能简单地等效为高导热系数的均匀导热体，因为压扁段的蒸汽层热阻不同于圆管段中的蒸汽层热阻。分段各向异性模型将部分压扁热管分为压扁段、突扩段和圆管段，如图1(a)所示。由于压扁段和圆管段分别涉及厚度方向、径向和轴向传热，因此在压扁段、圆管段设置了不同的各向异性的导热系数。因突扩段主要发生轴向传热，且长度很短，为方便计算在突扩段设置各向同性导热系数。计算各部分的导热系数如下:

图1 分段各向异性模型和分层分段模型Fig.1 Segmented anisotropy model and the layered-segmented model

(1)

(2)

式中：R、δ、A和k分别代表热阻、传热方向上的厚度、厚度方向上的传热面积和导热系数。下标wall、wick和flt分别代表热管管壁、吸液芯和压扁段。所以在厚度方向上的总导热系数为

(3)

圆管段径向热阻为圆管段管壁热阻和吸液芯热阻之和。圆管段管壁热阻和吸液芯热阻的计算如下：

(4)

(5)

式中：dwall,o和dwall,i为管壁外径和内径，dwick,o和dwick,i为吸液芯的外径和内径；下标cir代表圆管段。由于实验中圆形管侧面只有一半面积与冷却铜块接触，所以热阻应增大一倍。圆管段的径向热导系数计算如下：

(6)

上述管壁材料为铜，导热系数为398 W/(m·K)。吸液芯的有效导热系数将在第1.2节中讨论。热管的轴向导热系数设置为基于管壁、吸液芯和蒸汽层的横截面积的加权平均值。

(7)

式中,Across,tot为热管轴向方向总横截面积，下标a、cross和vap代表轴向方向、横截面和蒸汽层。蒸汽层的等效导热系数计算公式如下[14]:

(8)

式中：rvap、L、ρvap、Pvap、μ、Rg和T是蒸汽层的等效半径、蒸汽潜热、蒸汽的密度，蒸汽压力、动力粘度、蒸汽气体常数和蒸汽温度。圆管段截面的等效半径为蒸汽层的横截面半径。对于压扁段截面，蒸汽层的等效热导率计算如下[14]：

(9)

式中：dv为压扁段蒸汽层的厚度。

1.1.2 分层分段模型

分层分段模型将热管分为管壁层、吸液芯层和蒸汽层，如图1(b)所示。蒸汽层进一步被分为压扁段、突扩段和圆管段。上述各个部分均设置不同的各向同性导热系数。管壁层的导热系数为398 W/(m·K)；吸液芯导热系数的计算见第1.2节，蒸汽层导热系的计算见式(8)和式(9)。热管正常工作时，热管吸液芯与蒸汽界面处的相变热阻可以忽略[15]。

1.2 吸液芯模型

本研究选取了5种常用吸液芯等效导热系数(keff)计算模型(以下简称吸液芯模型)进行比较，分别是Parallel model、Peterson’s model、Alexander’s model、Yagi-Kunii’s model和Chi’s model见表1,kl、ks分别为液相、固相的导热系数，φ为相邻固相间传热速率的经验常数，ε为吸液芯孔隙率。其中Parallel model假设金属颗粒平行排列，吸液芯的有效导热系数最高。Peterson’s model、Alexander’s model、Yagi-Kunii’s model和Chi’s model都是经典的吸液芯等效导热系数计算模型[15,21]。上述吸液芯模型均假设吸液芯处于饱和状态，即液体工质充满吸液芯孔隙。由于在本研究的热管工作温度范围内，水的热物性随温度的变化不大，因此忽略温度对吸液芯等效导热系数的影响。

表1 饱和吸液芯等效导热系数Table 1 Effective thermal conductivity of saturated wick

2 实验和数值模拟

2.1 实验装置

本研究的热管总长度为220 mm，圆管段截面外径为6.0 mm，压扁段截面长度为130 mm，压扁段截面厚度为2.0 mm；管壁为铜，壁厚0.3 mm；吸液芯为烧结铜粉吸液芯，孔隙率为58%，厚度0.45 mm；热管工作流体为纯水。

实验系统包括加热装置、冷却装置和数据采集装置。加热装置由加热铜块、电加热棒和直流电源组成。加热铜块尺寸为长120 mm，宽20 mm，高23 mm，加热铜块内部有一个半径3.2 mm的圆柱形通道，用于放置一根长120 mm、半径3.0 mm的电加热棒。冷却装置由冷却铜块、恒温水箱、水泵和流量计组成。冷却铜块的尺寸为长60 mm，宽20 mm，高23 mm，上表面有一半径为3.1 mm的半圆形凹槽，用于放置热管圆管段。冷却铜块内部有一个半径为5.0 mm的冷却水流道。数据采集装置由K型热电偶(精度等级0.4)和安捷伦数据采集仪组成。如图2所示，热管水平放置，在热管下方是加热铜块和冷却铜块。在热管与铜块之间涂有导热硅脂(导热系数≥1.93 W/(m·K))。热管表面温度测点如图2所示。循环冷却水温度控制精度在±0.5 ℃以内。循环冷却水流速1 L/min，控制精度±0.05 L/min。整个测试装置采用保温材料包裹，热损失约为0.3 W。实验工况如表2所示。所有实验均在热管的极限功率范围内，即热管的整体温差不超过5 ℃[22]。

表2 实验工况Table 2 Experimental conditions

图2 热管测量实验系统示意图Fig.2 Schematic of the heat pipe testing system

2.2 数值模拟

2.2.1 几何模型

如图3所示，几何模型包括电加热棒、加热铜块、热管、冷凝铜块和循环冷却水。其尺寸与2.1小节中的实验装置尺寸一致。热管压扁段与加热铜块面接触，圆管段与冷凝铜块上表面的弧面凹槽接触，电加热棒插放在加热铜块的孔道中，循环冷却水流过冷凝铜块内的圆柱形流道。电加热棒发热，热量传递至加热铜块，再由热管传递至冷凝铜块，最后由冷却水带走。为了提高计算精度，对冷却水与铜块交界面附近的网格进行了加密；分段各向异性模型中热管压扁段厚度方向的网格设置3层；对分层分段模型，管壁层、吸液芯层和蒸汽层的网格分别设置3层。

图3 几何模型(单位：mm)Fig.3 Geometric model(Unit:mm)

2.2.2 控制方程

在仿真中，计算域为2.2.1小节中的几何模型。即加热铜块、加热棒(内部设置体积热源)、冷却铜块、冷却水和热管。其中热管采用等效导热模型，与加热铜块、冷却铜块和加热棒一样被设置为固体。循环冷却水设置为流体。仿真过程为稳态过程，时间项为0。固体计算域的能量控制方程如下:

(10)

冷却水域的能量控制方程为

(11)

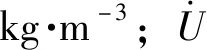
(12)

式中：u、v、w分别是x、y、z方向上的速度。

动量守恒方程如下:

(13)

式中:ν为水的运动粘度，m·s-2；P为压强，Pa；因过程为稳态，等式左边时间项为0。

2.2.3 边界条件

本实验条件下，冷却水雷诺数Re<2 300，为层流状态。冷却水通道进口为质量流量进口，进水温度采用实验测量值，冷却水通道出口为压力出口，相对压力为0 Pa。在热管与铜块的接触面之间、铜块与加热棒接触面之间为导热硅脂涂层。热管与铜块之间硅脂厚度为0.1 mm，铜块与加热棒之间硅脂厚度为0.2 mm。硅脂的导热系数为2 W/(m·K)，接触面设为耦合面。加热棒设置为体积热源。

采用Fluent 17.0软件进行仿真计算。为了保证数值模型的准确性，进行了网格独立性分析。如图4所示，纵坐标为热管表面最大温差，横坐标为网格数，当网格数从14 223增加到242 041时，热管蒸发段与冷凝段表面的最大温差变化小于0.5%。因此选择14 223网格数进行模拟计算。

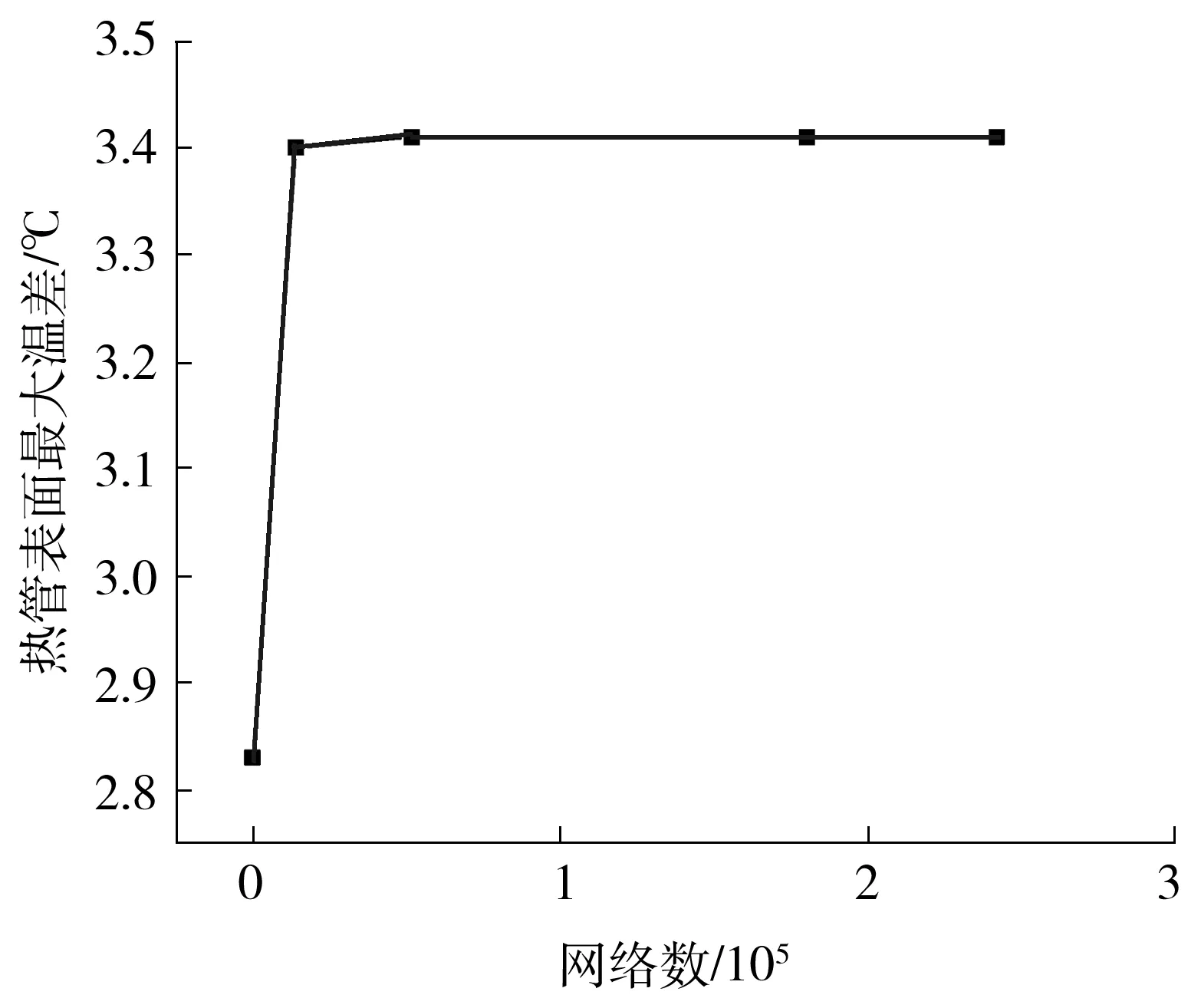
图4 网格独立性分析Fig.4 Grid independence test

3 结果与讨论

为了方便讨论，下面提到的最大相对误差(e)是实验温度与计算温度之间的最大相对误差。

(14)

为模型定义了编号，如表3所示。示例：Mo-del S-1表示等效导热的模型采用分段各向异性模型，而吸液芯模型采用平行模型(Parallel model)。

表3 部分扁平热管模型编号Table 3 Symbols for models of partially flattened heat pipe

3.1 分段各向异性模型的准确性

图5给出了热管工作温度为28、33、38、44、50 ℃时，采用不同吸液芯模型对分段各向异性模型的影响。可以看出，随着热管工作温度的升高，热管表面的最大温差越来越小。这是因为轴向导热系数主要取决于蒸汽的导热系数，当热管工作温度越高，蒸汽的导热系数越大，因此热管的表面温差就越小。此外，从图5还可以看出，随着热管工作温度的升高，表面温度逐渐接近冷却水温度。高热管工作温度导致高轴向导热系数，而轴向导热系数与蒸汽的导热系数成正比。在分段各向异性模型中，热管等效为固体，当厚度和径向的导热系数相对于轴向导热系数足够小时，意味着热量q很难传递到热管内部。大部分热量只传递到热管底部的“薄层区域”，然后沿轴向传递，如图6所示。图6是轴向的导热系数远高于厚度和径向的导热系数情况下，分段等效导热模型的热阻网络模型。R表示热阻，下标h-cop、c-cop、rad、δ、exp、a，和t分别表示加热铜块、冷却铜块、径向、薄层区域、突扩段、轴向和厚度方向。在这种情况下，因为热阻R与厚度δ成反比关系，当厚度足够小时，导致径向热阻足够小。在热阻网络模型中，圆管段温度可表示为

图5 不同热管工作温度下分段各向异性模型的仿真结果和实验结果对比Fig.5 Comparison of the simulated and experimental values of the segmented anisotropy model at different heat pipe operating temperatures

图6 轴向等效导热系数远大于径向导热系数时的热阻网络模型Fig.6 Thermal resistance network model where thermal conductivity in axial direction is much higher than that in thickness and radial direction

Tcir=Tw+qRc-cop+qRrad,δcir

(15)

式中：T和q为温度和热流量，下标cir、w、c-cop、rad和δcir 代表圆管段、冷却水、冷却铜块、径向方向和圆管段“薄层区域”。由上式可以看出，热管的径向导热系数较低，轴向导热系数较高，圆管段表面温度更接近水温。图7(a)为采用Model S-1、工作温度为28 ℃时的热管表面温度云图，图7(b)为采用Model S-5，工作温度为50 ℃时的热管表面温度云图。由图7(b)可以看出，对于Model S-5、当热管工作温度为50 ℃时，在厚度方向上存在温度梯度。在图7(a)中，温度在厚度方向上比较均匀。对于Model S-1，在热管工作温度为28 ℃时，厚度方向和轴向导热系数与轴向导热系数的比值相对于Model S-5在热管工作温度为50 ℃时的比值更大。热量可以在厚度方向充分传递，然后再沿轴向传递。从图8可以看出，采用Model S-1、Model S-2和Model S-3，在热管温度38 ℃及以下时，最大相对误差小于5.90%，而在热管工作温度高于38 ℃时其准确性降低。可见，分段各向异性模型的准确性受热管工作温度影响。

图7 热管表面温度云图Fig.7 Temperature contour of heat pipe surface

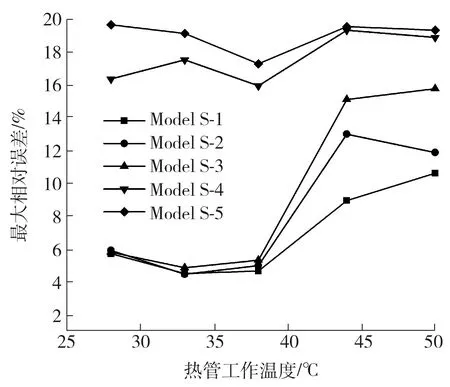
图8 热管工作温度对分段各向异性模型精确性的影响Fig.8 Effect of the heat pipe operating temperature on the accuracy of the segmented model

采用Model S-4和Model S-5，在不同的热管工作温度下，最大相对误差超过了15.94%。径向的导热系数取决于吸液芯和管壁的导热系数，Model S-4 和Model S-5采用Yagi-Kunii’s model和Chi’s model计算吸液芯等效导热系数，导致径向导热系数相对于轴向导热系数非常小，大部分热量只传递到热管底部的“薄层区域”，然后向轴向传递，如图6所示。

3.2 分层分段模型的准确性

由图9可知，当热管工作温度为28～50 ℃时，采用Model LS-1，Model LS-2，Model LS-3和Model LS-4时的最大相对误差范围分别为2.72%～6.51%、2.66%～6.44%、2.10%～5.25%和6.42%～11.54%。分层分段模型与分段各向异性模型不同，在分层分段模型中，其传热过程与热管实际传热过程相近，热流主要通过管壁层和吸液芯层传递至蒸汽层后沿轴向方向传热，再经圆管段的吸液芯层和管壁层传递至冷却铜块。如图10所示，根据热电比拟的思想，热流主要沿热阻最小的路径传递，所以分层分段模型不会出现分段各向异性模型中热流量主要在热管底部“薄层区域”传递的情况。圆管段温度可以表示为

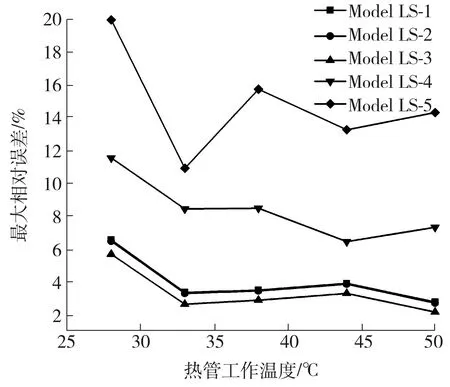
图9 热管工作温度对分层分段模型精确性的影响Fig.9 Effect of the heat pipe operating temperature on the accuracy of the layered-segmented model

Tcir=Tw+qRwall+qRwick

(16)

式中：Rwall和Rwick为管壁热阻和吸液芯热阻。其中管壁和吸液芯的厚度是确定的，Rwall和Rwick是定值，由式(16)可知，圆管段温度Tcir不会像在分段各向异性模型中，因Rrad,δcir足够小而更接近于冷却水温度。在不同热管工作温度下，采用Model LS-4和Model LS-5的表面温度远高于采用Model LS-1、Model LS-2和Model LS-3的表面温度，采用Model LS-3的表面温度略高于采用Model LS-1和Model LS-2的表面温度，而采用Model LS-1和Model LS-2的表面温度比较接近，其中采用Model LS-5的最大相对误差均超过10.89%，如图11所示。从表1可知，Model LS-5中采用Chi’s model计算的吸液芯等效导热系数，相比其他四个吸液芯模型计算的吸液芯等效导热系数是最小的，这表明其吸液芯层热阻更大，根据热电比拟的思想，如图10所示，吸液芯层的热阻越大，蒸汽层和管壁层的热阻不变，且蒸汽层热阻远小于管壁层和吸液芯层热阻，则经过蒸汽层这一传热路径的热流q越大，压扁段温度Tflt可以表示为

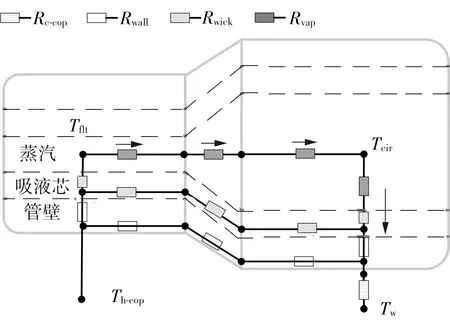
图10 分层分段模型的热阻网络模型Fig.10 Thermal resistance network of layered segmented model

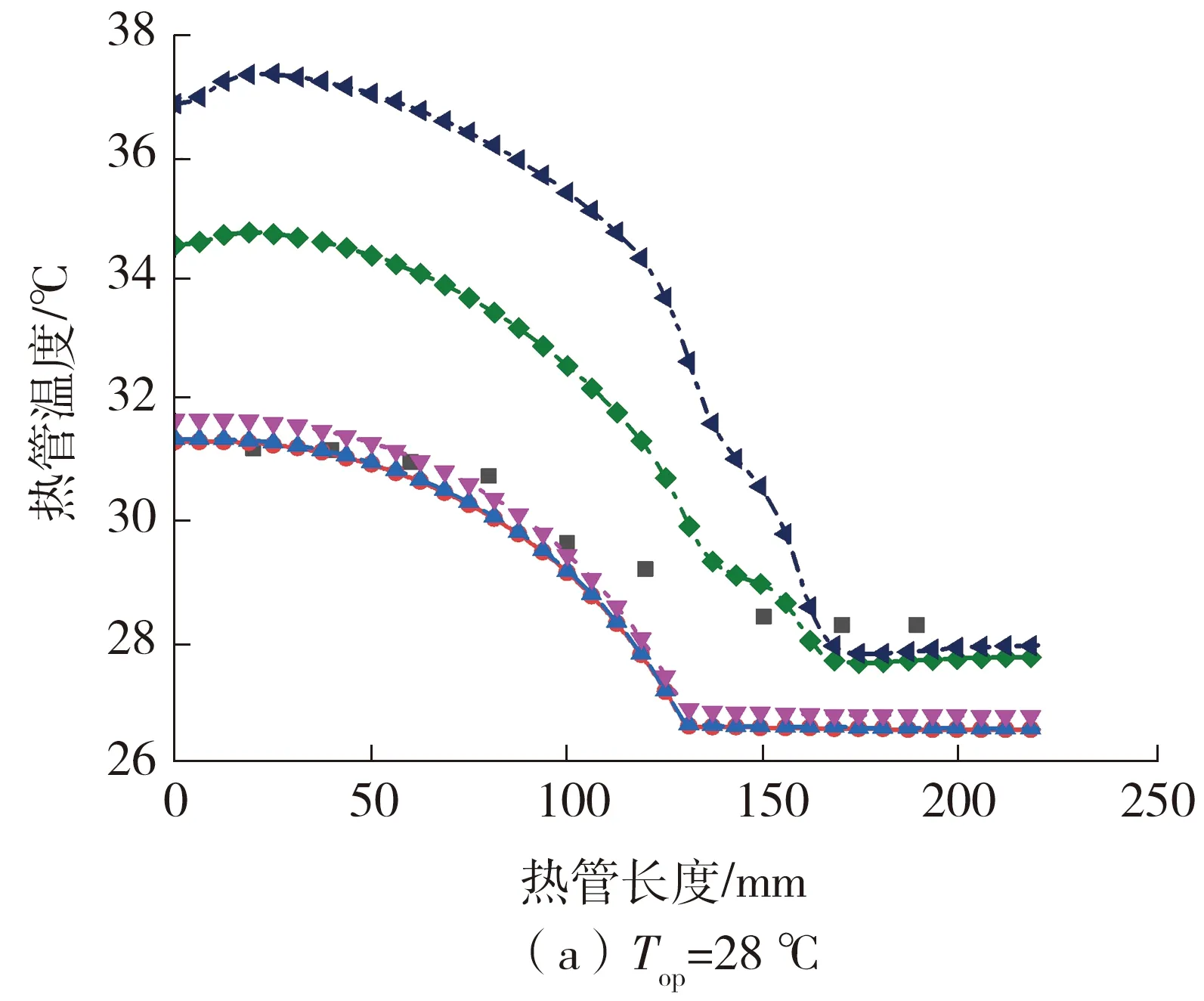
图11 不同热管工作温度下分层分段模型的仿真结果和实验结果对比Fig.11 Comparison of the simulated and experimental values of the layered segmented model at different heat pipe operating temperatures

Tflt=Tcir+q(Rvap,flt+Rvap,cir)

(17)

显然，当吸液芯等效导热系数越小时，q越大，分层分段模型的热管温差越大，如图10所示，从而计算得出的压扁段温度Tflt更加偏离实验测的压扁段温度。

3.3 分段各向异性模型与分段各向同性模型的对比

在3.1小节中讨论了分段各向异性模型的准确性，得知分段各向异性模型的准确性受热管工作温度影响。因为现有的研究中，很多文献在仿真计算中把热管视为各向同性导热系数的固体导体，故本小节加入分段各向同性等效导热模型进行对比。分段各向同性模型将热管分为压扁段、突扩段和圆管段，并分别设置各向同性等效导热系数，这里的等效导热系数设置为轴向等效导热系数。如图5所示，采用分段各向异性模型的表面温度随着热管工作温度的上升，逐渐偏离实验测试结果，更加接近冷却水温度。原因在3.1小节中已有讨论，在高热管工作温度工况下(Top=44 ℃和Top=50 ℃，因为分段各向异性模型轴向等效导热系数远大于径向等效导热系数，模拟计算过程中出现大部分热量只沿热管底部的“薄层区域”传递的情况，导致圆管段径向热阻即式(15)中Rrad,δcir足够小，圆管段温度接近冷却水温度。而分段各向同性模型中，径向和轴向的等效导热系数相等，在径向方向和厚度方向上热量能够充分传递，Rrad,δcir不可忽略，热管圆管段温度Tcir和冷却水温度Tw之间存在差值，从而热管温度更接近实验温度而不是冷却水温度。

定义参数Φ=kcir,rad/ka为径向等效导热系数与轴向等效导热系数的比值。图12为分段各向异性模型在不同热管工作温度下，不同的参数Φ值对其准确性的影响，其中Φ=1时的分段各向异性模型即是分段各向同性模型。从图12(a)可以看出，在热管工作温度为28 ℃、34 ℃和38 ℃时，最大相对误差在Φ略小于10-4处出现转折，在Φ大于10-4时逐步稳定。从图12(b)可以看出，在热管工作温度为44 ℃和50 ℃时，最大相对误差在Φ略小于10-3处出现转折，在Φ大于10-3时逐步稳定。从图12也可以看出，当热管轴向导热系数远大于径向导热系数时，分段各向异性模型的准确性会受到影响。