基于堆叠稀疏自动编码器和SVM的CSI室内定位方法

2021-12-07张会清王宇桐

北京工业大学学报 2021年12期

张会清，王宇桐

(1.北京工业大学信息学部，北京 100124； 2.数字社区教育部工程研究中心，北京 100124；3.城市轨道交通北京实验室，北京 100124)

通信技术的飞速发展与智能设备的普及，使基于位置的信息服务在现代社会中得到了进一步推广，随之而来的是对定位服务准确性与稳定性的更高要求[1]. 在定位服务体系中，室外定位系统日臻成熟. 然而在植被、建筑外墙等障碍物的阻碍下，室内接收机很难收到准确可靠的卫星信号，使得卫星导航难以应用于室内位置服务. 鉴于现代人生活平均有80%的时间处于室内场景，在复杂室内环境下准确获取位置信息具有广阔应用前景.

人们生活环境中Wi-Fi信号的覆盖极广，设备搭建简易，成本低廉，因此，Wi-Fi室内定位技术具有广阔的发展前景[2]. 在IEEE 802.11n协议[3]下正交频分复用(orthogonal frequency division multiplexing, OFDM)技术在频域会将通信链路划分为多个正交子信道，信号在发射端被分配到不同子载波上进行叠加后并行传输，在接收端通过快速傅里叶变换解调复现[4-5]. 信道状态信息(channel state information, CSI)是物理层通信链路属性，本质为每个载波上的衰弱因子，包含功率衰减、相位偏移等信息，记载了无线信号的多径传播过程，是对信号传播过程的细粒度描述. 无线信号多径结构具有独特性，因此，CSI可作为定位系统中描述不同物理位置的唯一标签[6]. 近年来，基于CSI的室内定位技术越来越受到研究者重视，通过指纹匹配、测距建模等原理实现了一些定位系统[7-9]. 其中指纹匹配定位方案避免了复杂的传播模型建模过程，一定程度上减少了非视距效应的不良影响，逐渐成为研究热点.

CSI指纹匹配定位技术包含离线建立指纹数据库以及在线实时定位2个阶段，离线阶段需在不同参考点采集接入点(access point, AP)信号，结合当前物理坐标生成指纹数据存入数据库. 在线阶段通过预测算法对实时CSI完成位置估计. 即便CSI能够作为更细粒度的信号指纹，现阶段基于CSI的室内定位方案仍存在缺陷：复杂环境下信道的不确定衰落影响了数据稳定性；Wi-Fi多天线结构使CSI数据维度高，占用存储空间大；等等.

针对上述问题，Xiao等[10]使用各天线子载波上CSI的功率均值作为物理位置表示，建立定位指纹库，减少了信号波动带来的负面影响，实时定位阶段通过概率模型完成定位；Chapre等[11]提出的CSI-MIMO利用信道时变性，在离线阶段将CSI在子载波、收发天线维度的幅值相位信息进行数据融合，使用融合数据的相对变化量作为定位依据建立新型指纹库，在在线阶段通过机器学习模型解算目标位置；Wang等[12-13]提出的DeepFi、PhaseFi在离线阶段分别解析了CSI的幅值数据与相位数据. 首先，通过训练受限玻尔兹曼机(restricted Boltzmann machine,RBM)采集二分图网络权重并将其作为指纹数据；然后，压缩指纹库体积，在在线阶段使用实时数据训练RMB，获取网络权重；最后，通过贝叶斯分类器实现指纹匹配，进一步提升了定位精度.

本文针对CSI数据室内定位应用中存在数据冗余大、解析复杂的问题，将表示学习引入指纹定位的特征提取任务，提出了基于堆叠稀疏自动编码器(stacked sparse auto-encoder, SSAE)[14]结合支持向量机(support vector machine, SVM)[15-16]的CSI室内定位方法SSAE-SVM. 单AP采集的CSI经预处理输入SSAE后，取编码网络部分的输出向量作为初始指纹的低维稀疏表示，建立稀疏特征指纹库；将指纹库作为模型训练集，通过SVM建立稀疏指纹与实际物理位置的映射关系. 该方案能够在压缩指纹库体积的同时进一步提升CSI室内定位系统的运行效率与精确度.

1 基于SSAE-SVM的CSI室内定位方法

1.1 方法结构

本文提出的定位方法包括离线与在线2个阶段. 离线阶段需要对CSI指纹进行采集与预处理，通过迭代训练更新SSAE特征提取网络权值矩阵，建立稀疏特征指纹库并训练SVM分类模型；在线阶段需要对用户实时采集的CSI流数据进行预处理，然后使用离线阶段保存的SSAE网络模型与SVM分类器完成稀疏编码、位置解算，最终输出定位坐标. 具体定位系统结构如图1所示.

图1 定位系统结构Fig.1 Principle of positioning system

1.2 CSI数据采集与预处理

通过开源工具[17]修改网卡底层驱动，可通过支持IEEE 802.11n标准的商用无线网卡以数据包形式采集收发设备间CSI. 数据包内为复数形式的CSI矩阵，可用于后续幅值、相位信息的解析. OFDM信道在频域可近似建模为

Y=HX+n

(1)

Hi=|Hi|ej∠Hi

(2)

式中：Y表示接收信号向量；X为发射信号向量；H为CSI矩阵；n为高斯噪声向量；i为子载波序号；幅值信息|Hi|为功率衰减的映射；相位信息∠Hi为相位偏移.

在环境干扰、设备不稳定、信道不确定衰落等因素的影响下，直接提取的幅值与相位信息包含异常值，对定位精度有很大影响.本文采用Hampel滤波器[18]对CSI幅值信息进行滤波处理，计算表达式为

(3)

并对初始CSI数据以一定间隔划分滑动窗口.式中：ai,j为第i个滑动窗口的第j个幅值数据；mi为第i个滑动窗口的中位数；e为可调节的权重因数；Di为中值绝对误差(median absolute deviation, MAD)，是第i个窗口中各数据对mi差值的中位数.图2为滤波前后位置不变情况下某天线对不间断采集50个数据包解析出的载波幅值的叠加图形.图中横轴为子载波序号，20 MHz频宽下OFDM系统中信道被划分为30个子载波；纵轴为不同数据包的载波幅值.可见该算法能够实现对异常值的准确识别，同时具有比例不变性，能够为数据质量带来有效提升.

图2 滤波前后幅值波形Fig.2 Amplitude waveform before and after filtering

由于收发设备存在时钟同步误差，中心频率不一致，不同周期载波相位存在重叠现象，导致CSI相位测量值与真实值存在残差[19].假设第i个子载波的采集相位为i，则有

(4)

(5)

某天线对原始相位、线性变换校正后的相位波形对比如图3所示.

图3 校正前后数据相位波形Fig.3 Phase waveform before and after correction

鉴于CSI中幅值与相位信息量纲不一致，若同时提升神经网络收敛效率，则初始位置指纹需要进行归一化

(6)

式中：fi,j为第j个指纹特征的第i个数据点；max(fj)、min(fj)分别为第j个指纹特征的全局最大、最小值.归一化后的CSI指纹联立生成初始指纹数据库，准备进一步进行特征提取.

1.3 SSAE稀疏特征提取与建库

为满足实际需求，需对CSI数据进行特征选择. CSI数据在特征空间呈非线性，不适合采用主成分分析法(principle component analysis, PCA)等线性降维方法[21]. 针对上述问题，设计搭建了基于堆叠稀疏自编码器(sparse auto-encoder, SAE)结构的深层编码网络SSAE作为特征提取算法. 每个离线指纹库中的指纹数据作为样本输入特征提取网络，通过迭代训练优化样本的重构误差，最终取SSAE网络输出的稀疏向量作为实际使用的定位指纹. SSAE算法本身鲁棒性强，提取的定位指纹具有低维稀疏性，能够在凝练有效特征的同时兼具低空间占用.

自动编码器(auto-encode, AE)的基本结构为3层对称神经网络，如图4所示. 设初始CSI指纹为n维向量x，编码输出为d维向量h，解码输出为n维向量y.编码输出h为

图4 自动编码器基本结构Fig.4 Basic structure of auto-encoder

h=g(Wx+b1)

(7)

得到编码压缩输出h后，解码输出y为

y=g(Vh+b2)

(8)

式中：函数g为激活函数；W、V分别为编码器与解码器的权重矩阵；b1与b2为两者偏置向量.在上述基础上，通过在代价函数中增加KL(Kullback-Leibler)散度[22]引导输出向量稀疏获得稀疏自动编码器.KL散度计算公式为

(9)

对初始指纹数据集X中的指纹x，设p(x)为期望稀疏指纹分布，q(x)为初始指纹真实分布，两分布的匹配程度与KL散度输出值成正相关.SAE网络收敛期望解码输出变量能够尽量无损地重构输入样本,代价函数通过重构误差结合期望分布与样本分布KL散度计算得来，公式为

(10)

式中：x(i)为第i个训练样本；y(i)为第i个解码输出；m为指纹样本总数；β为稀疏项系数；p为稀疏常数，用于代表期望的稀疏分布；qj表示编码器输出值中第j个特征的平均激活度.训练阶段通过反向传播迭代更新权值矩阵.当最终重构误差达到全局最小值时，认为输出的稀疏编码为原始样本的潜在空间表示.

SSAE编码网络层与层之间的映射关系由多个SAE编码部分组成，下层网络映射对象为上层SAE的编码输出. 解码网络结构与编码网络结构成镜像对称，最终输出重构样本. SSAE具有深度网络的强拟合能力，将特征提取转换为逐层递进过程，逐步逼近低维编码表示的最优解. SSAE基本网络结构见图5.

图5 SSAE网络基本结构Fig.5 Basic structure of SSAE network

本文特征提取网络SSAE的训练主要分为以下2个过程.

1) 贪心逐层预训练.

每次针对一个SAE进行迭代训练，取得网络参数后保存，输出向量作为下组SAE的输入，进而建立深度网络. 预训练目的为最小化每个编码层对上层输出的重构误差，降低每个编码层输出对原始指纹样本的信息损耗.

2) 微调.

建立与编码网络结构成镜像对称的解码网络，然后直接对整体深度网络进行反向传播迭代训练，并对网络参数进行进一步优化调整，最小化解码复现数据与原始数据的重构误差.

逐层预训练与微调激励了每个隐层输出对原始数据的关系，弱化了冗余特征与噪声影响，使编码网络尾层输出成为原始指纹数据的低维稀疏表示[23]. SSAE稀疏特征提取与建库的具体流程如下所述.

步骤1确定学习率、各隐含层层数、各层神经元个数等参数. 设置各层预训练迭代次数Ep、微调迭代次数Ef等网络参数，搭建SSAE网络.

转发锦鲤的背后，是人们对吉祥欢乐、好运的向往，尽管只有千万分之几乃至更低的中奖几率，这种人性的需求是不会过时的。此外，转发一条企业的相关微博，并不需要很高的成本，也不需要花费很多的时间成本，因此即便是小概率的中奖几率，加上锦鲤的寓意以及吸引力极强的礼单，使得人们都抱有试一试的心态，是一种“高投机性行为”。

步骤2输入初始CSI指纹数据，为当前隐层建立编码- 解码结构，生成临时SAE. 设置编码器激活函数为sigmoid函数，对输入指纹z的输出为

(11)

解码器同样使用sigmoid函数作为激活函数.

步骤3结构确定后开始进行无监督预训练，更新层间权值、偏置矩阵.网络权值更新采用反向传播法，更新表达式为

(12)

(13)

步骤4进入下一隐层，重复步骤2、3，直到所有隐层对应SAE全部训练完毕.

步骤5将已生成网络的权重矩阵作为初始化值，在网络末尾添加相反结构的解码网络，权值矩阵为编码网络的转置，重新训练深度网络并对网络整体进行权值微调，迭代次数为Ef.

步骤6舍弃解码网络，保存编码网络模型. 取编码网络尾层输出数据作为最终CSI指纹，生成稀疏特征指纹库.

1.4 SVM定位模型构建

wTφ(x)+b=0

(14)

(15)

式中：ξi为松弛变量；C为惩罚因子.采用拉格朗日乘子法求解二次规划问题，得

(16)

式中λi、μi为拉格朗日乘子.新目标函数对(w,b,ξi)是无约束问题，使其目标函数对变量(w,b,ξi)导函数为0并带回原函数.至此最优化问题化简为

(17)

目标函数通过核函数k代替内积运算过程.选择核函数为径向基函数(radial basis function, RBF)，映射方程为

(18)

式中参数γ为自由参数，用于控制单个训练样本在目标函数求解过程中的影响程度.核函数方法既为SVM分类器提升了非线性拟合能力，同时避免了在高维特征空间计算内积消耗大量的运算资源的问题.最终结合最优超平面函数与符号函数sign得到分类判别函数

(19)

在线定位阶段，SVM模型的输入为CSI实时稀疏编码，最终定位结果取为SVM输出定位结果的加权均值.假设分类器在某参考点共输出N个分类结果，每个分类器输出为(xl,yl)，l∈[1,N]，则最终定位结果计算方式为

(20)

2 实验结果与分析

为验证本文提出方法的有效性，选择了北京工业大学科学楼1021实验室作为实际实验场景，实验面积16 m×6 m. 该场景下布置有较多的桌椅、书柜、隔断板等物品. 平面图如图6所示，在定位区域以1 m为间隔共设置了56个参考点建立初始指纹库，用作定位算法的初始训练集与验证集. 图中黑色星型为视距(line of sight,LOS)指纹测试点，白色星型为非视距(non line of sight,NLOS)指纹测试点，每个参考点处以100 ms的采集间隔采集500个数据包. 同时在该覆盖范围内随机设置29个额外参考点采集测试数据，LOS参考点17个，NLOS参考点12个. 每个额外参考点以100 ms为采集间隔采集200个数据包. 其中，定位性能综合评价标准为平均定位误差以及误差的累计分布函数(cumulative distribution function，CDF).

图6 实验区域平面Fig.6 Plan of experimental area

实验设备采用装有三天线Intel 5300 AGN无线网卡的个人电脑，信号发射端为TP-LINK三天线无线路由器，经开源工具CSI TOOL修改网卡驱动后进行CSI数据采集. 定位算法通过Pytorch深度学习工具库结合Libsvm工具包开发实现. 确定网络深度后，使用粒子群优化算法确定各层神经元个数，设置初始离散种群粒子数为60，加速常数c1=c2=1.5，惯性因子0.85，粒子最大飞翔速度0.20，最大迭代次数为200，适应度函数设置为样本重构误差，粒子收敛后获得SSAE网络结构. 参与对比实验的SVM分类器均通过十折交叉验证与网格搜索确定最优参数. 经调优验证，设置SSAE网络隐层l=2，网络结构为540-269-113-40，指纹维度为40，预训练每轮编码层迭代次数为150，整体微调迭代次数为200. 设置SVM惩罚因子C=0.9，核函数k为RBF函数，核函数中自由参数γ=0.001. 最终采用的稀疏指纹集较原始CSI所占空间下降92.6%.

2.1 SSAE提取稀疏指纹特征对定位精度影响

为验证不同自动编码器结构提取的稀疏特征对定位精度影响，搭建了不同结构的特征提取网络进行定位误差对比实验. 如表1所示，对照实验定位算法分别选取未进行特征提取、经AE单层网络特征提取、经SAE单层网络稀疏特征提取、经SSAE深层网络稀疏特征提取的CSI指纹库与SVM分类器结合，进行误差对比与分析. 由实验结果可见，经过自编码器特征提取后的定位系统取得了更好的定位效果. SAE、SSAE提取的指纹特征平均定位误差较AE分别提升了31.7%与42.5%. SSAE平均定位误差达到1.205 m，在不同规模测试样本集中均获得了最优定位精度. 这一结果的出现是由于深层神经网络具有更强的数据拟合能力，在此基础上SSAE的稀疏性使新指纹空间内局部特征表征能力增强，提升了特征学习与分类器效率.

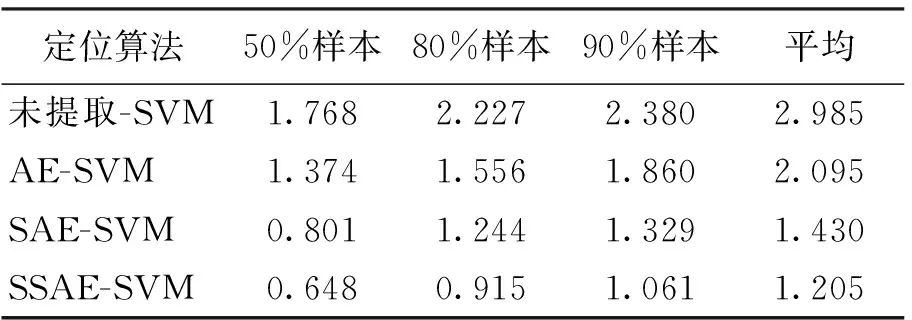
表1 不同结构自编码器结合SVM的定位误差对比Table 1 Comparison of positioning errors between different auto-encoders and SVM m

SSAE指纹提取后的特征维度数对定位精度同样有较大影响. 设SSAE输出指纹空间维度为k，取值范围设置为10～100. 如图7所示，定位误差首先随着k的增大逐渐减小，在k=40处出现拐点，此时定位误差为1.205 m；随后定位误差呈类似阶梯形式的上升. 可见定位误差与k无线性关系，这一现象是由于特征过少使编码过程更容易损失有效信息，过高的维度则易引入噪声特征，降低分类器效率.

图7 不同k值设置对应的平均定位误差Fig.7 Change of the average positioning error with the change of k

2.2 SVM核函数对定位精度影响

SVM核函数为分类器带来区分线性不可分数据的能力，因此，核函数的选择对SVM准确率、时间消耗具有较大影响. 鉴于指纹数据集具有高维线性不可分性，同时Wi-Fi信号在稳定环境下的阴影效应遵循正态分布，本文选择RBF作为SVM的核函数. 为证明其有效性，本实验将其与常用核函数：Linear、Sigmoid、Poly进行对比. 对比结果如表2所示，RBF核SVM得到了最小的平均定位误差.

表2 不同核函数SVM定位误差与定位耗时对比Table 2 Comparison of positioning error and positioning time between different kernel functions

Linear核SVM尽管能够在极短时间内实现定位，但会将平均定位误差提升0.319 m，定位效果差.

2.3 SSAE-SVM算法与其他定位算法的性能对比

2.3.1 不同特征提取算法效果对比

本文将SSAE定位方法与传统线性特征提取算法PCA和奇异值分解(singular value decomposition,SVD)、非线性特征提取算法核主成分分析(kernel principle component analysis,KPCA)进行了性能对比. 对比算法均通过交叉验证与网格搜索在解空间调整为最优参数，其中KPCA、PCA均将指纹空间压缩至35维，SVD压缩至45维，KPCA核函数为RBF. 如图8所示，实验结果表明本文方法的定位误差范围与精度均优于其他算法. 由于PCA与SVD均为线性非监督降维模型，在CSI指纹数据上表现相近且效果不佳. SSAE与KPCA均具有非线性拟合能力，更适用本文采用的数据集，但KPCA本质是使用核矩阵代替内积矩阵的PCA算法，核函数映射能力带来的效果提升有限，导致最终定位效果虽优于线性降维模型但仍造成较大的累积误差.

图8 不同特征提取算法累积概率分布Fig.8 Different feature extraction algorithms cumulative probability distribution

2.3.2 不同分类器定位性能对比

在稀疏特征指纹库的基础上，将本文算法与多种分类器算法进行比较. 对照算法包含决策树(decision-making tree, DT)、随机森林(random forest, RF)、梯度提升树(gradient boosted decision tree, GBDT)，各算法均经过网格搜索调优参数设置. 如图9与表3所示，可以看出SVM在稀疏指纹集上能实现更为准确的定位. 本文算法较GBDT将定位误差下降约34.3%，较KNN下降约17.4%. 实验中DT模型普遍定位精度较低，部分测试点出现了严重误判. 这是由于在稀疏指纹集中，DT模型基于信息熵的贪心节点分裂策略具有误导性，破坏局部特征关联.

图9 不同定位算法在SSAE稀疏指纹集上的累积概率分布Fig.9 Cumulative probability distributions of different localization algorithms on SSAE sparse fingerprint sets

表3 不同算法在SSAE稀疏指纹集上的定位误差对比Table 3 Comparison of positioning errors between different algorithms on SSAE sparse fingerprint sets

表3给出了相同测试环境下各算法的单点平均定位耗时. 本文实验的采集设备为DELL个人电脑，实验环境为Ubuntu 12.04LTS系统，硬件配置采用Intel Core i5 3210M CPU，主频2.5 GHz，内存8 GB. 本实验中KNN定位算法的单点定位耗时最高，这是由于KNN在定位阶段会将实时指纹与指纹库内指纹进行了全量的距离运算，导致定位效率低下. 实验中其他的定位算法耗时较为相似，尽管结构相对简单的DT模型定位耗时较少，但其定位精度难以满足应用场景的定位需要. 本文定位算法位置解算平均耗时0.695 s，能够在常见室内场景下兼顾实时性与高精确度.

2.3.3 LOS、NLOS定位效果分析

表4给出了LOS与NLOS测试点下本文方法定位效果，并与CSI-MIMO[11]指纹提取方案结合KNN与SVM定位算法的效果比较. 实验表明，LOS环境下各算法均能达到比NLOS环境更好的定位效果. 由于CSI-MIMO特征提取依据为相邻采集数据包间信道幅值、相位信息的变化情况，NLOS下CSI随机衰落较为明显，导致该算法定位精度较差. 本文方法在LOS与NLOS环境中定位误差均低于CSI-MIMO，在LOS环境中平均定位误差比CSI-MIMO结合SVM的定位方案降低0.492 m，比NLOS环境下降低1.071 m，综合平均定位误差降低约37.4%.